EXAMINATION OF BALL TRACKING AND CATCHING TASK

USING A MONOCULAR VISION-BASED MOBILE ROBOT

Fumiaki TAKAGI, Fumio MIYAZAKI

Graduate School of Engineering Science, Osaka University

Toyonaka, Osaka 560-8531, JAPAN

Ryosuke MORI

Graduate School of Information Science, Tohoku University

Sendai, Miyagi 980-8579, JAPAN

Keywords:

Ball catching, monocular vision, non-holonomic, mobile robot, visual feedback.

Abstract:

This paper presents an implementation of a ball catching task using a monocular vision-based mobile robot.

We have proposed a motion strategy for catching a ball ﬂying in three-dimensional space. This strategy has

its roots in the ﬁeld of experimental psychology but is more powerful and concentrated on a robot. A practical

trajectory control law is derived for a non-holonomic mobile robot to track and catch a ball. This control law

educes the full potential of the motion strategy: we experimentally demonstrate that a monocular vision-based

mobile robot, coping with the problem due to its non-holonomic constraint, successfully catches a ball.

1 INTRODUCTION

“What information does the ﬁelder sense and how

does the ﬁelder run to the right spot in order to catch

a ﬂy ball?” This problem has interested researchers in

various ﬁelds, namely physics, experimental psychol-

ogy, and robotics. Around 40 years ago, Chapman,

physicist, pointed out that the ﬁelder runs so as to

maintain the rate of change of tangent of the elevation

angle of the ball (Chapman, 1968). Recently, some

researches in experimental psychology have shown

evidence that partly supports Chapman’s hypothesis

(McLeod and Dienes, 1993; McLeod et al., 2003).

From a viewpoint of control, some researchers have

studied the formulation of human catching strategy in

connection with perceptual feedback control. Tresil-

ian examined how Chapman’s strategy behaves under

the limiting conditions of human through simulations

(Tresilian, 1995). Borgstadts and Ferrier focused on

how to implement Chapman’s strategy and carried out

experiments using a mobile robot considering only

the case where the ﬁelder exists in the ﬂying ball tra-

jectory (Borgstadts and Ferrier, 2000). Marken also

formulated a perceptual-motor feedback law of hu-

man catching strategy which is slightly different from

Chapman’s strategy (Marken, 2001).

Additionally, McBeath et al. proposed a strategy

named linear optical trajectory (LOT) (McBeath et al.,

1995). Sugar et al. (including McBeath) introduced

the moving image plane and derived various travel-

ing control laws, some of which are based on LOT

and others are based on Chapman’s strategy. They

also performed experiments in which a mobile robot

tracks and catches a balloon or rolling a ball (Suluh

et al., 2001; Sugar and McBeath, 2001; Mundhara

et al., 2002; Mundhara et al., 2003).

On the other hand, we have proposed a new motion

strategy that is more powerful and concentrated on a

robot. Moreover we have implemented a trajectory

control law based on the architecture of visual servo-

ing and analytically showed the ability to track and

catch a ball (Miyazaki and Mori, 2004). However, in

the analysis, we assumed that

1. The horizontal velocity of a ball is negligible;

2. Image Jacobian is exactly available,

which are inadequate in real situation because as-

sumption (1) too much restricts ball’s motion and as-

sumption (2) is hard to be achieved in the monoc-

ular vision system. In this paper, we remove these

assumptions and then derive a new trajectory control

law that enables a monocular vision-based mobile ro-

bot to track and catch a ball. To demonstrate the valid-

ity of the proposed control law, experimental results

are also shown.

100

TAKAGI F., MIYAZAKI F. and MORI R. (2005).

EXAMINATION OF BALL TRACKING AND CATCHING TASK USING A MONOCULAR VISION-BASED MOBILE ROBOT.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 100-105

DOI: 10.5220/0001161801000105

 SciTePress

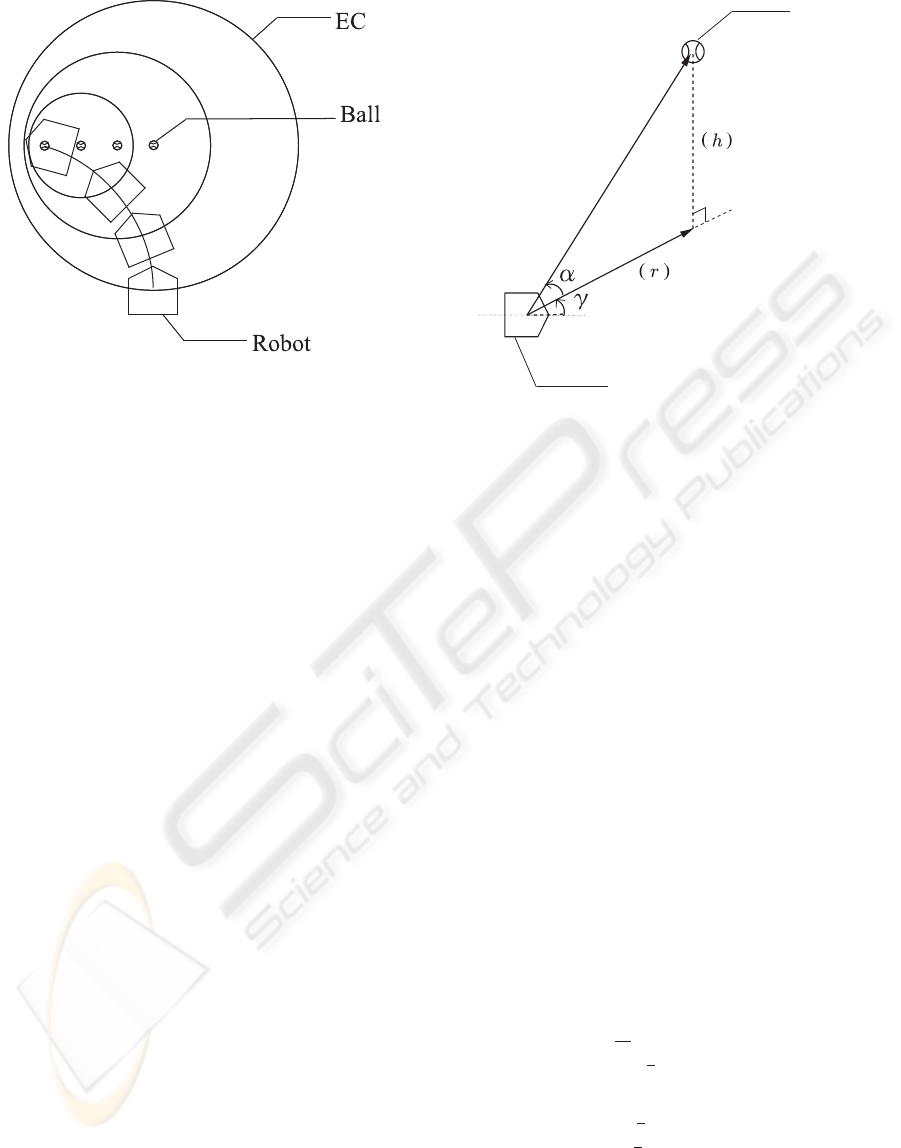
Figure 1: Concept of GAG strategy.

2 ABOUT GAG STRATEGY

We have proposed the motion strategy named GAG

(Gaining elevation Angle of Gaze), which states that

the ﬁelders selects a running path to keep the tan-

gent of elevation angle against the ball continuously

increasing. For the sake of intuitive understanding,

we show the schematic catching based on this strat-

egy in Figure 1. This ﬁgure shows a robot pursuing

the ball launched from the center to the left. The cir-

cle termed EC is the equiangular circle (i.e. the set

of points where the measured elevation angle remains

unchanged). It should be noted that “gaining the tan-

gent of the elevation angle of gaze continuously” cor-

responds to “decreasing the radius of EC”.

3 TRAJECTORY CONTROL FOR

BALL CATCHING

3.1 Kinematic model of the mobile

robot

We suppose a wheeled type mobile robot as a robotic

ﬁelder. In a typical model of a non-holonomic mo-

bile robot, the two driving wheels are independently

driven by two actuators to achieve the translation and

orientation. Using the translational velocity v and ro-

tational velocity ω, the kinematic equiation of this

model can be expressed as





˙x

˙y





cos θ 0

sin θ 0

0 1





, (1)

Robot

Ball

Figure 2: Relative position between the robot and the ball

where (x, y) and θ denotes the position and orienta-

tion of the mobile robot in a world coordinate frame

respectively.

3.2 Relation between the Robot and

the Ball

In this section, we formulate the rate of change in the

relative position/orientation between the robot and the

ball.

As shown in Figure 2, let α be the elevation angle

of gaze, and γ be the lateral angle of gaze. It should

be noted that these variables can be securely obtained

through a monocular vision system ﬁxed on the robot.

In order to analyze and evaluate the tracking perfor-

mance, we introduce the following two variables un-

available with the monocular vision system: r (the

horizontal distance between the robot and the ball)

and h (the height of the ball from the robot). Then,

the rate of change in these variables due to the robot’s

and ball’s motion can be described as

˙r

˙α

˙γ





− cos γ 0

sin 2α cos γ 0

sin γ −1

















w, (2)

where e is the unit vector on the line extending to the

center of EC from the robot, n is the vector obtained

by rotating e about a vertical axis counterclockwise

in the amount 90

◦

, l is the vector obtained by rotating

EXAMINATION OF BALL TRACKING AND CATCHING TASK USING A MONOCULAR VISION-BASED

MOBILE ROBOT

101

the unit vector on the line from the robot to the ball

about a line having the direction of n counterclock-

wise in the amount 90

◦

, and w is the velocity vector

of the ball. The ﬁrst term in the right hand side is

caused by the robot’s motion and the second term is

by the ball’s motion.

3.3 Control Law

The control law which implements GAG strategy is

given by

v = k

cos γ sin 2α (3)

ω = k

sin γ sin 2α, (4)

where k

, k

are the positive constants. This control

law has two advantages over the one we have already

proposed(Miyazaki and Mori, 2004): (i) The image

Jacobian is not required. (ii) Tuning parameters k

, k

are easily determined. The validity of this control law

is shown in the following section.

3.4 Ball Tracking and Catching

We explain the control law given by Eqs. (3), (4) en-

ables the mobile robot to successfully track and catch

a ball in the following three cases.

(A) A case that a ball is suspended in the air

Let us consider a case that a ball is suspended in the

air. The task objective in this case is to approach a

point just below the ball.

Substituting Eqs. (3), (4) (control inputs) into

Eq. (2) and setting w to be zero yields

˙r = −k

cos

γ sin 2α ≤ 0. (5)

Equality holds if and only if |γ| = π/2.

In case that |γ| = π/2, the robot has its an-

gular velocity ω = k

sin γ sin 2α, thus, ˙γ =

−k

sin γ sin 2α, which means the robot rotates in-

stantly and gets out of this situation. Moreover, the

robot stops (v = 0) if and only if it arrives at the

point just below the ball. As a result, the robot as-

ymptotically approaches to the point just below the

ball.

Here arises a simple question we can answer: what

path does the robot follow to track a ball? The curva-

ture of the path is given by

ρ =

tan γ (6)

and consequently proportional to the tangent of ball’s

lateral angle tan γ. Thus, the path of the robot sub-

ject to this control law varies according to the initial

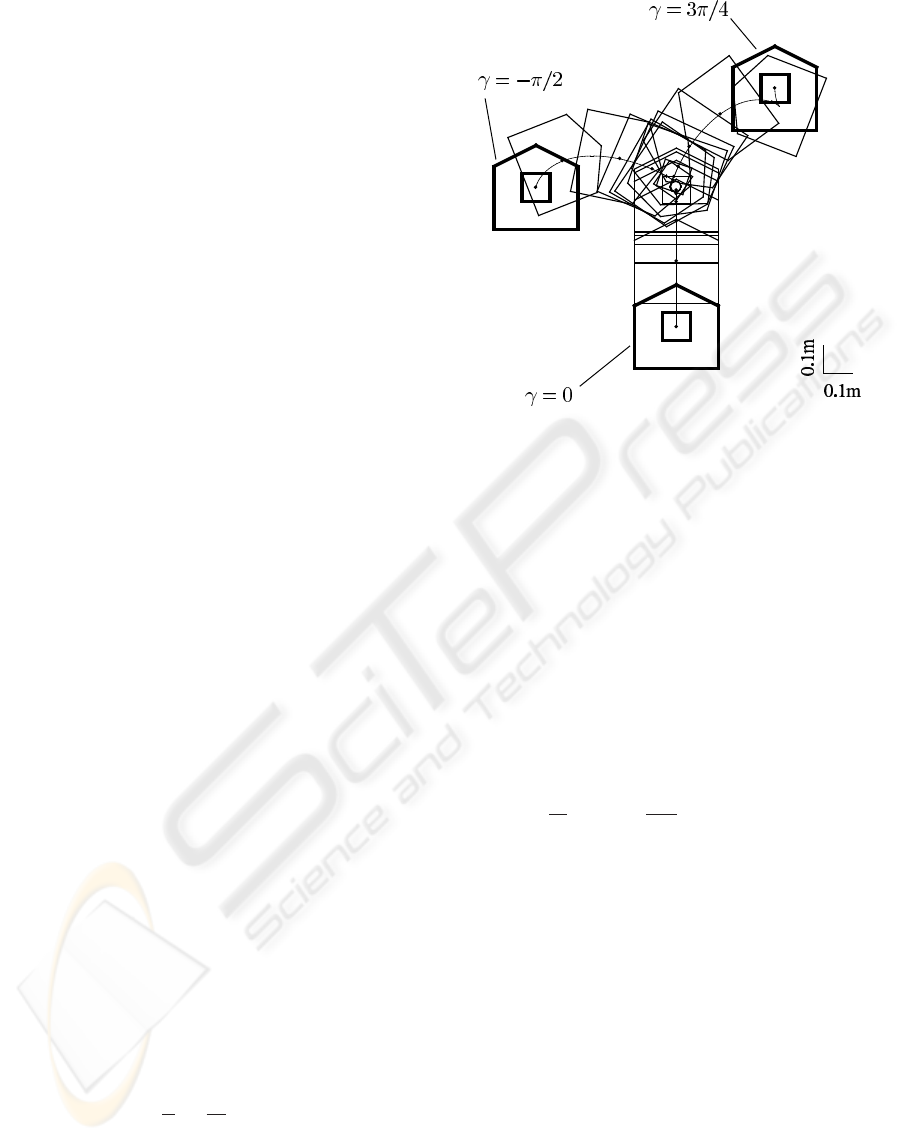
orientation, namely γ. Figure 3 shows various paths

in typical cases. The robot gets forward to just below

Figure 3: Typical paths of the robot subject to Eqs. (3), (4)

illustrated every 0.2 sec (k

= 1, k

= 13)

the ball if γ = 0. If 0 < γ ≤ π/2, the robot moves to-

ward the inside of EC and gets closer and closer to the

center of EC, though the robot does not know where

the center is. If π/2 < γ ≤ π , ﬁrst the robot ro-

tates toward the center of EC while getting backward,

and then starts getting forward after the orientation

becomes less than π/2, that is, 0 < γ ≤ π/2. In case

that γ has a minus sign, the robot moves in the same

manner except rotating inversely.

By the way, during the robot’s tracking, the tangent

of elevation angle is kept increasing. The reason is

that its time derivative

tan α =

cos

γ sin 2α, (7)

is always positive excepting |γ| = π/2. (In case that

|γ| = π/2, as already mentioned above, the robot

rotates instantly to satisfy |γ| < π/2.) This means

that the radius of EC asymptotically vanishes, in other

words the robot gets closer and closer to the point just

below the ball. This suspended ball case is regarded

as one of the special case among the general tracking

cases shown in Figure 1.

(B) A case that a ball rises and falls without

moving horizontally

Eq. (5) holds in this case as well as in the previous

case (A). This means that the path of the robot subject

to GAG is not dependent on the ball’s vertical motion,

provided that the ball does not move horizontally. In

other words, the path is uniquely determined by the

robot’s initial location and orientation as in the case

(A). Therefore the robot gets closer and closer to the

ICINCO 2005 - ROBOTICS AND AUTOMATION

102

point just below the ball so as to catch the ball. It

is the only difference between the case (A) and the

case (B) that the robot has to reach the catching point

before the ball falls onto the ground. Increasing the

gain k

, k

brings quick approaching to the catching

point, and then the robot maintains the path provided

the ratio of gain k

is kept unchanged.

horizontally

Finally, we explain the robot can catch the ball in gen-

eral case that the ball rises and falls while moving

horizontally. Substituting Eqs. (3), (4) (control input)

into Eq. (2) yields

˙r = −k

cos

γ sin 2α + e

w. (8)

If e

w ≤ 0, the robot approaches the point just below

the ball similarly to the case (B). This corresponds to

the case that the ball comes up to the robot. Next let us

consider the case that e

w ≤ 0, that is, the case that

the ball ﬂies away from the robot. In such a situation,

if γ ≃ 0 holds after pursuing the ball for a while, the

time derivative of r becomes

˙r = −k

sin 2α + kwk. (9)

Here, from sin 2α = 2hr/(h

+ r

), the distance be-

tween the ball and the robot converges to r

given by

hkwk

(10)

provided the gain k

is large enough in compari-

son with the ball’s horizontal velocity kwk. This

means that the robot approaches the ball according to

Eq. (10) and catches the ball when the ball falls onto

ground (r → 0 as h → 0).

In the meantime, from Eq. (2) and Eqs. (3), (4), we

get

˙γ =

sin γ cos γ sin 2α−k

sin γ sin 2α+

(11)

where the ﬁrst and second terms in the right hand side

are negative provided

−k

cos γ < 0 (12)

excepting the case that γ = π.

This means that, if

(13)

is satisﬁed, Eq. (11) gives

˙γ < −

(1 − cos γ) sin γ sin 2α +

w. (14)

This implies that |γ| remains small if the gain k

large enough compared with kwk

Figure 4: Path of the robot pursuing a ball

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

Time [sec]

r [m]

r (k

= 3, k

= 39)

Figure 5: Change in the distance to the ball

From condition Eq. (13) and r

given by Eq. (13),

we can conclude as follows: The horizontal distance

between the ball and the robot approaches the value

hkwk

(15)

provided that we choose large enough gains k

, k

satisfying

. (16)

To verify this analysis, we show simulation results

obtained by assuming that the ball moves under the

inﬂuence of gravity. Figure 4 shows typical paths of

the robot pursuing a ﬂy ball. From this ﬁgure, we can

see that GAG works well regardless of the robot’s ini-

tial location and orientation. The time histroy of the

radius of EC is given in Figure 5 for a certain pursuing

motion (corresponding to the green curve in Figure 4,

which demonstrates that the radius of EC decreases

according to the parabolic function of time given by

Eq. (10) (the dotted curve in Figure 5).

EXAMINATION OF BALL TRACKING AND CATCHING TASK USING A MONOCULAR VISION-BASED

MOBILE ROBOT

103

4 EXPERIMENT

We constructed a monocular vision-based mobile ro-

bot to verify our proposed method experimentally. An

IEEE1394 camera with a ﬁsh-eye lens and ball catch-

ing device are mounted on a mobile base that commu-

nicates with a desktop PC through RS-232C. The total

length and width of the mobile base are 300[mm] and

the maximum velocity is 2[m/sec]. The translational

and angular velocities of the robot are determined us-

ing the information extracted from 2D image, namely

elevation angle α and lateral angle γ by Eqs. (3), (4)

at the video rate, 33[msec]. The commands of the

translational and angular velocities are converted into

wheel velocities and transmitted from the desktop PC

to the mobile base and the motors of right and left

wheels are controlled by a servo controller on the mo-

bile base.

4.1 Method

The experimental procedures are as follows: The ball

is thrown by a person or a ball launcher. As soon as

the camera mounted on the mobile robot gets sight of

the ball, the robot begins running to catch the ball.

Every 33 [msec], the frame rate of the video camera,

the ball’s image is acquired and the velocity command

is sent to the robot. The moment the robot reaches the

catching point and then catches the ball, the ball gets

out of the sight and the robot stops.

4.2 Result and Discussion

We have carried out experiments to verify the effec-

tiveness of the proposed control law based on GAG

strategy. The following result demonstrates how the

robot behaves in a real situation.

The ball is thrown up about 50 [cm] in front of and

20 [cm] on the right of the robot. The result is shown

in Figure 6 and Figure 7. Figure 6 is a sequential pho-

tograph where the ball and the robot is extracted. In

Figure 7 the location of the ball and the robot is plot-

ted in a world coordinate frame. These results indi-

cate that a mobile robot subject to GAG successfully

catches a ball.

5 CONCLUSION

This paper presented an implementation of ball catch-

ing task using a monocular vision-based mobile ro-

bot: (1) Our proposed GAG strategy was employed

as a motion strategy to track a ball; (2) A practical

trajectory control law is derived for a non-holonomic

Figure 6: Ball catching by a wheeled mobile robot with

monocular vision system

−100

100

200

300

400

500

200

400

500

1000

1500

X [mm]

Y [mm]

Z [mm]

Figure 7: Path of the robot pursuing a ball

mobile robot to track and catch a ball, which is an im-

plementation of GAG strategy. Moreover, we demon-

strated that the robot can catch a ball ﬂying in three-

dimensional space using the monocular vision sys-

tem. This demonstration exempliﬁes the potency of

the GAG strategy and the practicality of its control

law.

The GAG strategy was devised aiming at robotic

ﬁelders rather than explaining of human catching

strategy. The robot subject to the GAG strategy is re-

quired to have the ability to run faster than the ball

for a reliable ball catching. However, we can utilize

GAG beyond baseball. For example, GAG is suited

ICINCO 2005 - ROBOTICS AND AUTOMATION

104

to autonomous navigation for mobile robots if we re-

gard a ﬂy ball as a marker in the environment. In the

autonomous rendezvous and docking task of space-

crafts, GAG can be extended to a simple and robust

onboard rendezvous control strategy by considering

a ﬁelder as a chaser spacecraft and a ball as a target

spacecraft.

REFERENCES

Borgstadts, J. A. and Ferrier, N. J. (2000). Interception of

a projectile using a human vision-based strategy. In

IEEE Int. Conf. on Robotics and Automation.

Chapman, S. (1968). Catching a baseball. American Jour-

nal of Physics, 36:868–870.

Hutchinson, S., Hager, G. D., and Corke, P. (1996). A tuto-

rial on visual servo control. IEEE Trans. on Robotics

and Automation, 12(5):651–670.

Marken, R. S. (2001). Controlled variables: psychology

as the center ﬁelder views it. American Journal of

Psychology, 114(2):259–281.

McBeath, M. K., Shaffer, D. M., and Kaiser, M. K. (1995).

How baseball outﬁelders determine where to run to

catch ﬂy balls. Science, 268:569–573.

McLeod, P. and Dienes, Z. (1993). Running to catch the

ball. Nature, 362:23.

McLeod, P., Reed, N., and Dienes, Z. (2003). How ﬁelders

arrive in time to catch the ball. Nature, 426:243–244.

Miyazaki, F. and Mori, R. (2004). Realization of ball catch-

ing task using a mobile robot. In ICNSC’04, 1st IEEE

International Conference on Networking Sensing and

Control, pages 58–63.

Mundhara, K., , Sugar, T., and McBeath, M. (2003). Per-

ceptual navigation strategy: A uniﬁed approach to in-

terception of ground balls and ﬂy balls. In IEEE Int.

Conf. on Robotics and Automation, pages 1689–1694.

Mundhara, K., Suluh, A., Sugar, T., and McBeath, M.

(2002). Intercepting a falling object: Digital video ro-

bot. In IEEE Int. Conf. on Robotics and Automation,

pages 2060–2065.

Sugar, T. and McBeath, M. (2001). Spatial navigation al-

gorithm: Application to mobile robotics. In Vision

Interface.

Suluh, A., Sugar, T., and McBeath, M. (2001). Spatial nav-

igational principles: Apprications to mobile robotics.

In IEEE Int. Conf. on Robotics and Automation.

Tresilian, J. R. (1995). Study of a servo-control strategy for

projectile interception. Quarterly Journal of Experi-

mental Psychology, 48:688–715.

EXAMINATION OF BALL TRACKING AND CATCHING TASK USING A MONOCULAR VISION-BASED

MOBILE ROBOT

105