IMPROVED STABLE FEEDBACK ANC SYSTEM WITH
DYNAMIC SECONDARY PATH MODELING
Rogelio Bustamante-Bello
1,2
, Héctor M. Pérez-Meana
1
(1) Graduate Studies Section. ESIME Culhuacán, Instituto Politécnico Nacional. 1000 Santa Ana Ave. San Francisco
Culhuacán, C.P. 04430, Ciudad de México, México.
(2) Instituto Tecnológico y de Estudios Superiores de Monterrey Campus Ciudad de México. 222
Del Puente St., Ejidos de Huipulco, C.P. 14380, Ciudad de México, México.
Bohumil Psenicka
Universidad Nacional Autónoma de México, Facultad de Ingeniería, P. O. Box 70-389, Delegación Coyoacán, C.P.
04510 Ciudad de México, México.
Keywords: Active Noise Control (ANC), stable feedback ANC systems, Normalized Filtered X LMS algorithm
(NFXLMS), feedforward ANC systems, Normalized Filtered X LMS algorithm with Noise Addition
(NFXLMS-NA).
Abstract: This paper presents the development and DSP implementation of a stable ANC feedback system with on-
line secondary path modelling, using the Normalized Filtered-X Least Mean Square with Noise Addition
algorithm (NFXLMS-NA), for acoustic noise cancellation. In this paper, the feedforward and the feedback
ANC systems are described briefly; the basic of the FXLMS algorithm and its structure is discussed and the
new NFXLMS-NA algorithm is presented. The ANC system developed includes a conventional noise
predictor, a primary adaptive filter, a subsystem for dynamic secondary path modelling and the addition of
white noise signal in the FXLMS algorithm in a novel structure looking for stability into the system. The
system was developed for cancelling quasi-periodic acoustic noise; some experimental results for narrow-
band signal are included in order to show the desirable feature (stability) of the system. Proposed system
was implemented using a TMS320C30 evaluation module from TI. Finally, the paper includes the block
diagram of the ANC system, the structure of the program used in the implementation and some photographs
of the practical scheme and the equipment used in the tests.
1 INTRODUCTION
The active noise cancellation (ANC) involves
electro acoustic or electro mechanic systems that
cancel the primary noise based on the superposition
principle. In fact, a “pseudo-noise” is generated with
same amplitude but with contrary phase of the
original noise to be cancelled in a specific area
(quiet zone); the ANC attenuates low frequency
noise where passive systems result to be no efficient
at all. The amount of cancelled noise depends on the
amplitude and phase of the control signal generated;
a more complete discussion of the principles of
ANC can be found in (Widrow et al., 1975) (Kuo
and Morgan, 1996) (Elliot, 2001) (Farhang-
Boroujeny, 1998) (Haykin, 1996) (Solo and Kong,
1995).
In the digital signal processing field, there are
two basic types which allow to implement ANC
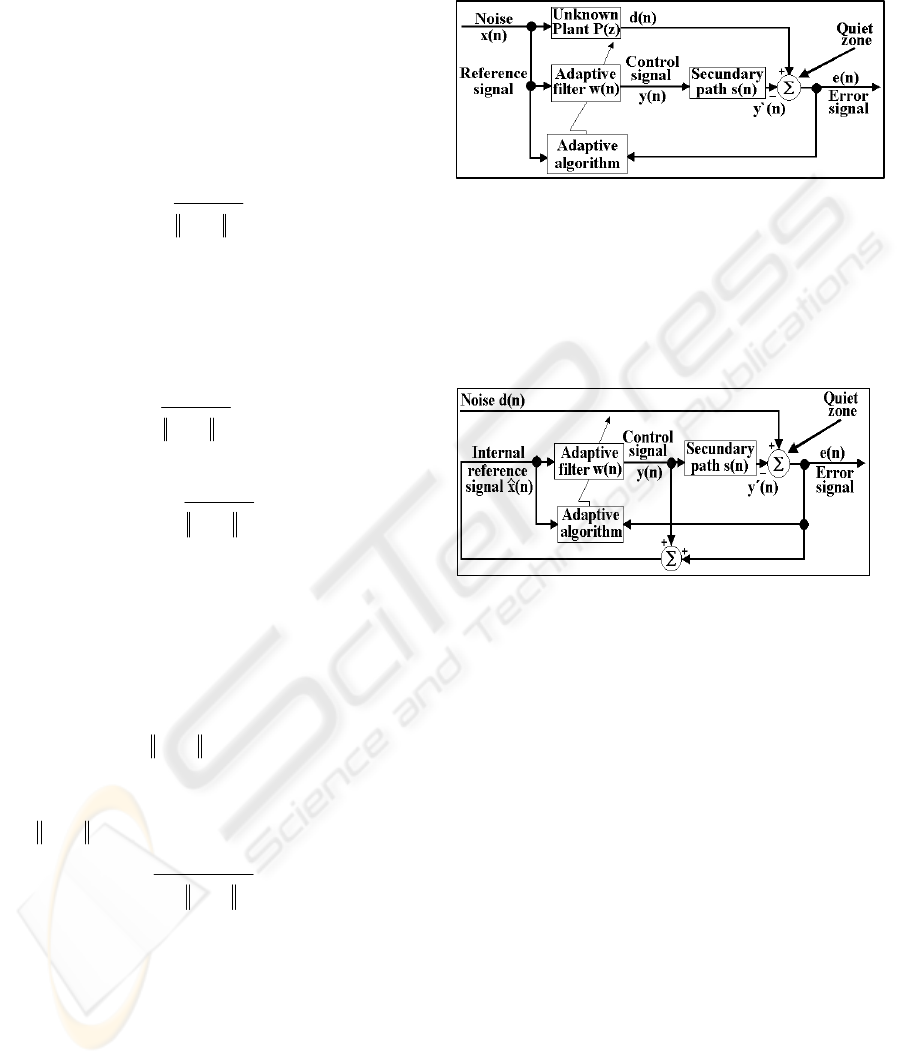
systems, feedforward and feedback ANC systems,
which are show in the blocks diagrams of Figs 1 and
2; in both systems, a digital filter coefficients vector
is adjusted to minimize an error signal, which is
stated as the noise signal minus the control signal.
A basic feedforward ANC system has two
sensors: one of these sensors picks up the primary
noise (also called the reference signal) on the
upstream of sound propagation and feed this signal
on to the system’s filter –the secondary source- in
order to generate a control signal. The system tries
to estimate the propagation paths –the primary path-
from the first sensor to second and, using the
reference signal, generate a signal to cancel out the
primary noise at the place of the second sensor –the
error sensor-.
191
Bustamante-Bello R., M. Pérez-Meana H. and Psenicka B. (2005).
IMPROVED STABLE FEEDBACK ANC SYSTEM WITH DYNAMIC SECONDARY PATH MODELING.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 191-199
DOI: 10.5220/0001162901910199
Copyright
c
 SciTePress

A feedback ANC system has only the error
sensor and its signal is used to reconstruct the
reference signal. This system uses an adaptive linear
predictor in order to generate its internal reference
signal; then, this signal is used by the filter to
generate a control signal. The proposed ANC system
only can estimate the signal present at the error
sensor and, since only narrow-band signals can be
predicted, this system is most effective to cancel out
narrow-band low-frequency noises (Kuo and
Morgan, 1996), (Elliot, 2001), (Haykin, 1996),
(Bustamante and Perez, 2002).
In both cases, adaptive algorithms are generally
used to estimate the filter coefficients that are
modelling the signals. In the digital signal
processing field, there are several adaptive
algorithms that allow to implement ANC systems;
however, the least mean square (LMS) type
algorithm originally proposed by Widrow (Widrow
et al., 1975) is the most popular in ANC systems for
its simplicity. This algorithm adjusts the coefficients
of a digital filter in order to minimize the signal
present at the error sensor.
However, in a real application, it is necessary to
know the path from the digital filter to the error
sensor because this path could change the control
signal. The basic ANC algorithm which considers
the effects of this path (usually called the secondary-
path),
)(zS is the Filtered-X LMS (FXLMS)
algorithm, in which the reference signal is changed
by a filter modelling the secondary-path and then it
is used by the LMS algorithm to estimate the
primary path model (Kuo and Morgan, 1996),
(Elliot, 2001), (Haykin, 1996).
Typically, the secondary path is estimated using off-
line modelling and then used in the ANC system.
Figure 1: Basic feedforward ANC system
Figure 2: Basic feedback ANC system
However, if the secondary-path is time-varying,
it is desirable to estimate this path on-line in order to
assure the stability and convergence of the adaptive
filter.
In this paper, we present the implementation of a
feedback system in a TMS320C30 DSP system
using a modified FXLMS algorithm. The secondary
path is estimated using on-line modelling and, in
order to enhance the stability of the system, white
noise is added to the FXLMS algorithm. Also, we
provide some experimental results of this ANC
system in a real environment. As an advantage, this
system use only one input and one output in order to
avoid the interference among the control signal and
the external reference signal presents in the
feedforward systems (Kuo and Morgan, 1996),
(Elliot, 2001), (Haykin, 1996), (Bustamante and
Perez, 2002), (Bustamante et al., 2003), (Rafaely
and Elliot, 1996).
2 THEORY
There are many algorithms that govern adaptive
filters in ANC systems. In the following proposal we
revise the basic theory of the Least Mean Square
(LMS) algorithm (Widrow et al., 1975) -
(Bustamante et al., 2003), the Normalized LMS
(NLMS) algorithm (Kuo and Morgan, 1996) -
(Haykin, 1996), the Filtered X LMS (FXLMS)
algorithm (Kuo and Morgan, 1996), (Elliot, 2001),
(Haykin, 1996), (Bustamante and Perez, 2002),
(Bustamante et al., 2003), the Normalized FXLMS
(NFXLMS) algorithm and the new NFXLMS with
Noise Addition (NFXLMS-NA); this last one
algorithm was used in our system in order to work
with the on-line identification process to modelling
the secondary path and, at the same time, get
stability into the system.
2.1 The LMS algorithm
This algorithm is one of the simplest regarding its
implementation, and in its simpler version, we have
the stochastic gradient LMS algorithm. Equations
(1)-(4) show the basic equations of the LMS
algorithm; its function is to search the optimum
adaptive filter coefficients
)(n
opt
ω
G
that minimize
the error signal )(ne . These equations show that it is
a recursive algorithm, which means that the present
value of the coefficients )1(
+nω
G
depends on the
previous one )(n
ω
G
; essentially, the LMS is a
gradient search based method (Widrow et al., 1975)
(Kuo and Morgan, 1996) (Elliot, 2001) (Farhang-
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
192

Boroujeny, 1998) (Haykin, 1996) (Solo and Kong,
1995).
[] )(
ˆ
)()1( nnn ξµωω ∇−=+
G
G
(1)
Where:
)()(2)()(
ˆ
2
nenxnen
G
−=∇=∇ξ
(2)
And
)()(2)()1( nenxnn
G
G
G
µωω +=+
(3)
It is important to notice that
µ
should not be
very large in order to avoid the method’s divergence,
but it also should not be very small so that the
convergence time results too long; a good choice for
µ
is:
max
1
0
λ
µ <<
(4)
Where
max
λ
is the maximum eigenvalue of the
input signal autocorrelation matrix.
The convergence speed depends on the
eigenvalues
i
λ
of the input signal autocorrelation
matrix. It is important to mention that the
eigenvalues of the input signal are related directly
with the power of the signal and every
i
λ
gives a
different convergence mode; from literature related
with this topic can be observed that the slower time
constant is given by eq. (5) (Widrow et al., 1975)
(Kuo and Morgan, 1996) (Elliot, 2001) (Farhang-
Boroujeny, 1998) (Haykin, 1996) (Solo and Kong,
1995). If there are large eigenvalues spread in the
input signal autocorrelation matrix, the algorithm
will have larger convergence times and, as a result, it
will not be useful for practical implementation.
min
4
1
max
µλ
τ =
(5)
s
s
Reference Signal’s Eigenvalues Dispersion. For
an ANC system with fast convergence, the input
signal autocorrelation matrix )]()([ nxnx
⊗ should
have the distribution shown in (6).
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
n
R
λ
λ
λ
"
#%##
"
"
00
0
2
0
00
1
(6)
The samples will be uncorrelated by obtaining a
diagonal matrix, making the LMS’s processing
easier. It is also required that the difference between
the eigenvalues
),...,,(
21 n
λλλ
is minimum in
order to achieve a very low dispersion coefficient. If
the autocorrelation matrix of input signal )(nx has a
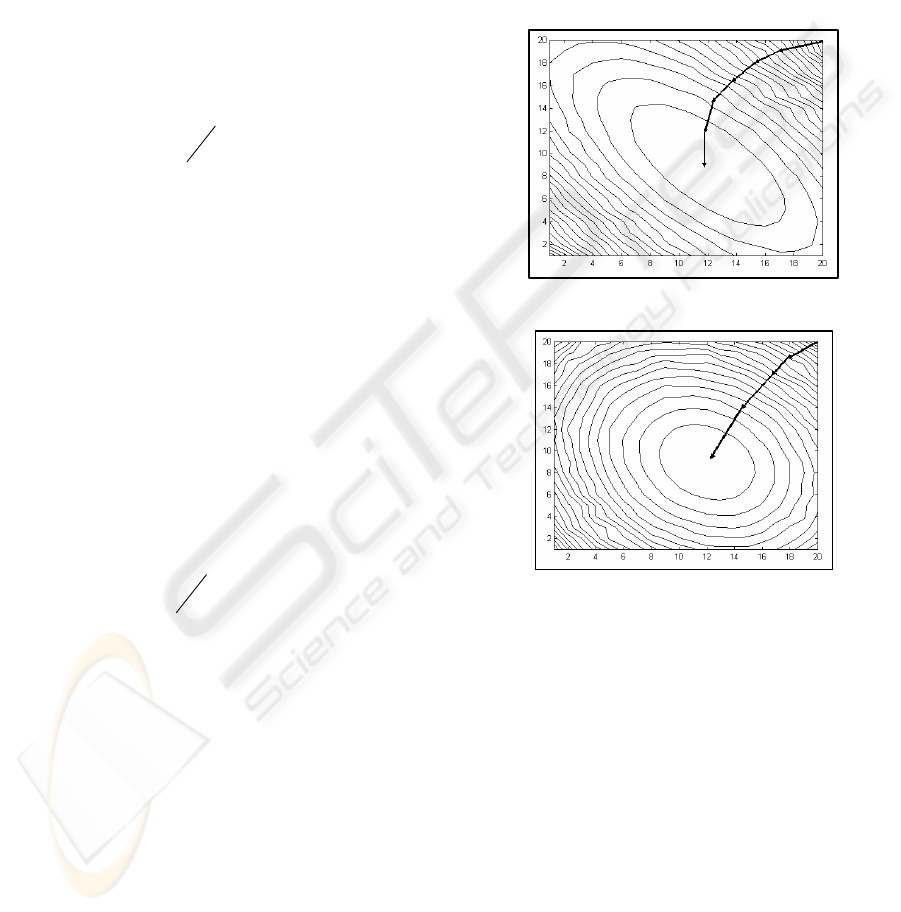
large eigenvalue spread, elliptical level curves result
within a two coefficients error surface. These curves
provide a larger trajectory to get to the center
(optimum solution), due to the fact that the
convergence direction found by the LMS is
perpendicular to the level curves (Fig 3). For a lower
eigenvalue spread the level curves acquire a near
circular form providing a shorter and more direct
trajectory to arrive to an optimum solution as it can
be seen in Fig 4. To achieve similar maximum and
minimum input signal’s eigenvalues
(
max
min
λλ ≈
) it is necessary to pre-process this
signal before introducing it to the algorithm.
Figure 3: Disperse eigenvalues’ level curves
Figure 4: Similar eigenvalues’ level curves
In our case, we added white noise to the
reference signal in order to change its characteristics
(Kuo and Morgan, 1996), (Elliot, 2001),
(Bustamante and Perez, 2002), (Bustamante et al.,
2003); it process will be explained ahead.
2.2 The Normalized LMS (NLMS)
Algorithm
The convergence time and stability of the adaptation
process of the LMS algorithm is governed by the
step size
µ
and the reference signal power (Kuo and
Morgan, 1996) (Elliot, 2001) (Farhang-Boroujeny,
1998) (Haykin, 1996). The maximum stable step
size
µ
is inversely proportional to the filter order
and the power of reference signal
)(nx
. One
important technique to do the stepsize independent
IMPROVED STABLE FEEDBACK ANC SYSTEM WITH DYNAMIC SECONDARY PATH MODELING
193

of the input signal while maintaining the desired
steady-state performance, independent of the
reference signal power, is know as the
normalized
LMS algorithm
(NLMS).
The algorithm NLMS consists on adjusting the
coefficients
)(n
ω
G
in the iteration (n + 1) using a
correction factor
() 1+∆ n
ω
G
that is “normalized” in
accordance with the square norm of the values of the
reference signal
)(nx
in the iteration n (eq. 7).
)()1()1( nnn
ω
ω
ω
GGG
−+=+∆
)()(
2
)(
1
nenx
nx
G
G
=
(7)
To control the change in the coefficients
)(n
ω
G
from an iteration to another without changing their
direction, it is introduced a real positive factor of
scaling denoted by
ψ
. This is, the change
() 1+∆ n
ω
G
is redefined as:
()
)()(
2
)(
1 nenx
nx
n
G
G
G
ψ
ω =+∆
(8)
Then, the NLMS algorithm is expressed as:
)()(
2
)(
)()1( nenx
nx
nn
G
G
G
G
ψ
ωω +=+
(9)
where 0 <
ψ
< 2.
It is important to emphasize that the NLMS
algorithm presents a convergence rate potentially
faster than the LMS algorithm with correlated or
decorrelated input samples. On the other hand, when
the values of the reference signal
)(nx
are small,
numeric problems are presented when
ψ
is dividing
for a small value of
2
)(nx
.
To solve this problem, the form of the NLMS
algorithm is modified adding a constant value to the
norm
2
)(nx
, according to the eq. (10).
)()(
2
)(
)()1( nenx
nxa
nn
G
G
G
G
+
+=+
ψ
ωω
(10)
Where a > 0.
2.3 The Filtered-X LMS (FXLMS)
Algorithm
As it was mentioned in section 1, since the
secondary path transfer function
)(zS
follows the
adaptive filter
)(zW
, the LMS algorithm must be
modified to ensure convergence (Kuo and Morgan,
1996), (Elliot, 2001), (Haykin, 1996), (Rafaely and
Elliot, 1996), (Zhang et al., 2001). Figures 5 and 6
show the feedforward and the feedback ANC system
with the secondary path
)(ns
.
Figure 5: Basic feedforward ANC system with secondary
path
There are different possible schemes that can be
used to compensate the effect of
)(ns
. The most
common scheme is to place an estimated filter
)(
ˆ
ns
in the reference signal path to the weight update of
the LMS algorithm, which realizes the usually called
Filtered-X LMS (FXLMS) algorithm.
Figure 6: Basic feedback ANC system with secondary
path
In order to obtain the equations that control the
FXLMS algorithm, we begin with the equation of
the error signal
)(ne
; according to the Fig. 5:
)()()()()()( nynsndnyndne ∗−=
′
−=
)]()([)()( nxnnsnd ∗∗−= ω
(11)
According to eq. (2) and using the eq. (11) for the
error signal, we get the gradient estimated for the
FXLMS algorithm:
)()(2)(
ˆ
nenxn
′
−=∇
G
ξ
(12)
Where
)(nx
′
is the filtered reference signal and
is given by:
)()()( nxnsnx ∗=
′
(13)
Substituting Eq. (12) into Eq. (1), we get the
equation of the FXLMS algorithms for the
feedforward ANC system:
)()(2)()1( nenxnn
′
+=+
G
G
G
µωω
(14)
For the feedback ANC system, we can write the
equation for the FXLMS algorithm, as follows:
)()(
ˆ
2)()1( nenxnn
′
+=+
G
G
G
µωω
(15)
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
194

Where
)(
ˆ
nx
′
, the estimated filtered reference
signal, is given by:
)(
ˆ
)()(
ˆ
nxnsnx
∗=
′
(16)
The estimated reference signal
)(
ˆ
nx
is showed
in the block diagram of the Fig 8 and it will be
compute later.
Figure 7: Feedforward ANC system with real secondary
path and estimated secondary path
Figure 8: Feedback ANC system with real secondary path
and estimated secondary path
Feedforward and feedback systems with off-line
estimated secondary path are showed in blocks
diagrams of Figs 7 and 8.
2.4 The Normalized FXLMS
(NFXLMS) Algorithm
Because the normalization technique optimizes the
convergence speed of the LMS algorithm, this
technique is used with the FXLMS algorithm in
order to improve the adaptation process. Equation
(17) shows the NFXLMS algorithm used in our
feedback ANC system.
)()(
ˆ
2
)(
ˆ
)()1( nenx
nxa
nn
′
′
+
+=+
G
G
G
G
ψ
ωω
(17)
2.5 The FXLMS Algorithm and the
Secondary Path ModelLing
The FXLMS algorithm requires knowledge of the
transfer function
)(zS
. There are two main
techniques to estimate that transfer function, the off-
line modelling and the on-line modelling; both
schemes are discussed briefly ahead (Kuo and
Morgan, 1996), (Elliot, 2001), (Haykin, 1996),
(Rafaely and Elliot, 1996), (Zhang et al., 2001).
2.5.1 Off-line modelling
Assuming that the characteristics of
)(zS
are time-
invariant but unknown, off-line modelling can be
used to estimated the secondary path during an
initial training stage. White noise is an ideal
broadband training signal in system identification
because it has a constant spectral density at all
frequencies; at the end of the training interval, the
estimated model
)(
ˆ
zS
is fixed and used for ANC
operation. Because this technique was not used in
our system, it will not be described anymore, but in
references (Kuo and Morgan, 1996), (Elliot, 2001)
there are some examples about the characteristics of
this technique.
2.5.2 On-line modelling
In some applications, the secondary path
)(zS
may
be time-varying. For this reason, it is desirable to
estimate the secondary path when the ANC system
is in operation, in order to assure the stability and
convergence of the adaptive filter. There are
different techniques to do that, but the more useful
technique is when the system use additive white
noise as an excitation signal for on-line modelling,
because those signal has a constant spectral density
at all frequencies.
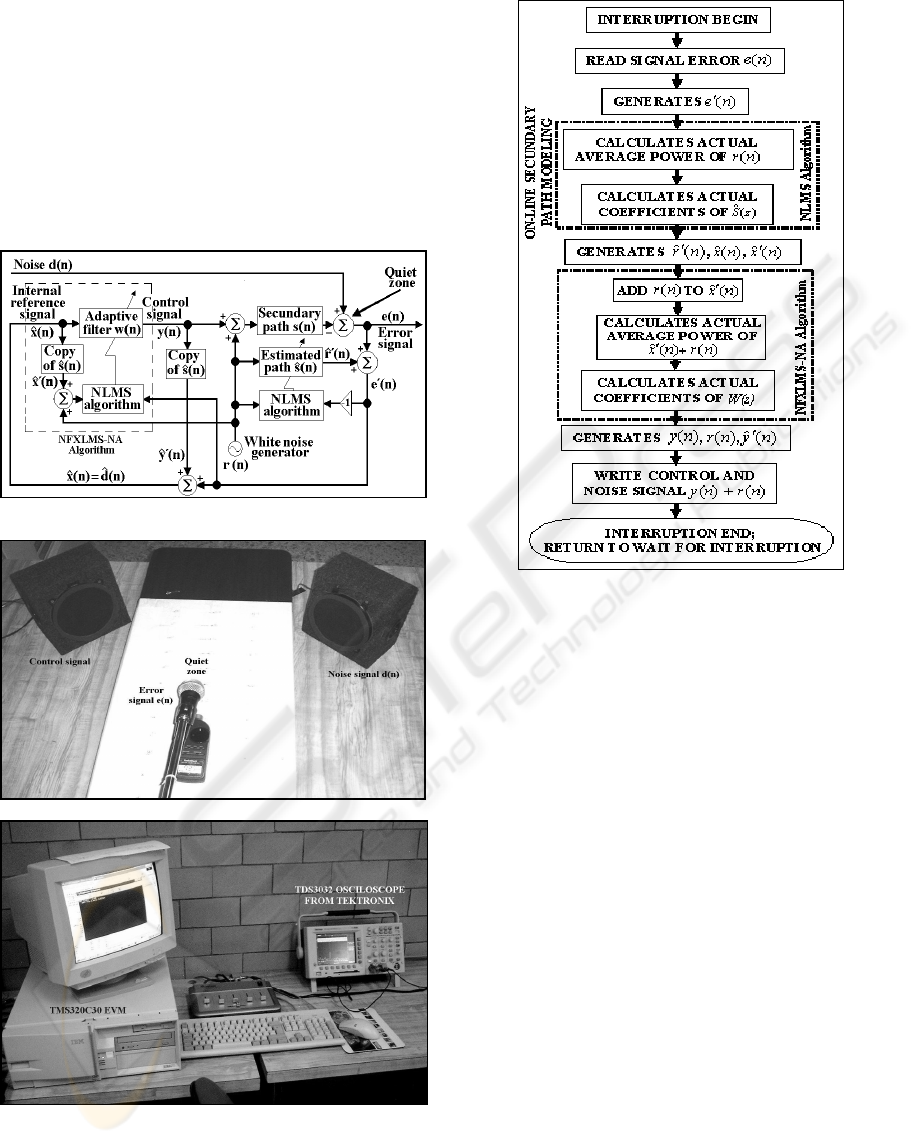
A feedback ANC system using the FXLMS
algorithm with adaptive on-line secondary-path
modelling is showed in Fig. 9. A random noise
generator is used to generated a zero-mean white
noise )(nr that is uncorrelated with the estimated
primary noise )(
ˆ
nx . The white noise signal is added
to the control signal )(ny produced by the adaptive
filter )(nw to drive the secondary source. The
adaptive filter )(
ˆ
ns is connected in parallel with the
secondary path in order to be able to model
)(zS
.
The input signal used for modelling )(
ˆ
ns is the
random noise )(nr .
The error signal at quiet zone is expressed as:
)()()()()()( nrnsnynsndne ∗−∗−=
)´()´()( nrnynd −−=
(18)
IMPROVED STABLE FEEDBACK ANC SYSTEM WITH DYNAMIC SECONDARY PATH MODELING
195

Where )(ny
′
is the secondary noise component
due to the original noise and )(nr
′
is the secondary
noise component due to the additive random noise.
An estimate of )(nr
′
, )(
ˆ
nr
′
, is calculated from
the modelling filter
)(
ˆ
zS
and the signal
)(nr
,
according with the eq. (19):
)()(
ˆ
)(
ˆ
nrnsnr ∗=
′
(19)
Figure 9: Feedback ANC system with on-line secondary-
path modelling
Assuming that
)(
ˆ
zS
is a good approximation,
that is
)()(
ˆ
zSzS ≈
, we have
)()(
ˆ
nrnr
′
≈
′
and the
)(ne
′
signal is given by:
)(
ˆ
)()()()( nrnrnyndne
′
+
′
−
′
−=
′
)()( nynd
′
−≈
(20)
At the same time, we get the estimated filtered
control signal )(
ˆ
ny
′
from
)(
ˆ
zS
and )(ny :
)()()(
ˆ
)(
ˆ
nynynsny
′
≈∗=
′
(21)
Finally, we generate the internal reference signal
(estimated signal) )(
ˆ
nx adding the estimated
filtered control signal )(
ˆ
ny
′
to )(ne
′
, according
with the eq. (22):
)(
ˆ
)(
ˆ
)()(
ˆ
ndnynenx =
′
+
′
=
(22)
This last signal is processing with the NFXLMS-
NA algorithm (next section) in order to update the
coefficients of the adaptive filter
)(zW
.
2.6 The NFXLMS-NA Algorithm
Since the control signal )(ny is feedback internally
(in the system) across the estimated secondary path
in order to generated the estimated reference signal
)(
ˆ
nx , and because )(ns could have error in its
estimation, the system could be unstable. In (Rafaely
and Elliot, 1996), it is showed that
“an adaptive
controller can be made robustly stable by an
appropriated level of stabilising noise”
. In that
article, the stabilising
noise is added to the filtered
estimated reference signal )(
ˆ
nx
′
before those
signals cross the )(
ˆ
ns filter. In the paper, some
results of this technique with a fixed secondary path
are showed (Bustamante and Perez, 2002),
(Bustamante et al., 2003).
Instead of that and according with our
development, we (a) added the random noise
)(nr
to the filtered estimated reference signal )(
ˆ
nx
′
before the updated of the coefficients of the adaptive
filter )(nw and (b) the coefficients of the secondary
path are updated dynamically (on-line secondary
path modelling) in a real environment; Fig. 10 shows
this process.
With these changes, we propose the NFXLMS
algorithm with Noise Addition (NFXLMS-NA); the
recursive equation of the NFXLMS-NA algorithm is
derivate using eq. (17) and Fig. 10:
)(
2
)()(
ˆ
)]()(
ˆ
[
)()1( ne
nrnxa
nrnx
nn
GG
G
G
GG
+
′
+
+
′
+=+
ψ
ωω
(23)
Figure 10: Feedback ANC system NFXLMS-NA based
In section 4 are showed the results of the
NFXLMS-NA algorithm.
3 IMPLEMENTATION
Practical feedback ANC system (NFXLMS-NA
based) was implemented using the TMS320C30
evaluation module (EVM) from TI. Characteristics
of the implemented system are the following:
a) The secondary path
)(zS
was an open
environment and it was estimated using the NLMS
algorithm with 500 coefficients.
b) The adaptive filter
)(zW
was estimated using
the NFXLMS-NA algorithm with 500 coefficients
c) The white noise
)(nr
used had an effective
value of 100 milivolts (Vrms).
d) The sampling frequency of the A/D had a
1milisecond period.
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
196

e) Different tonal signal between 150 y 500 Hz,
with
f∆
equal to 50 Hz, was used as noise
Fig. 11 illustrates the block diagram of the ANC
system (NFXLMS-NA based); Fig. 12(a) show the
practical scheme and Fig. 12(b) show the DSP board
and part of the equipment used in the
implementation.
In order to have an efficient implementation, we
used assembler language for C30 DSP in the
development of the program; in Fig. 13 is showed
the structure of the main program.
Figure 11: block diagram of the implemented ANC system
12 (a)
12 (b)
Figure 12: (a) Practical scheme and (b) DSP board and
equipment utilized in the implementation
.
Figure 13: Structure of the main program
4 TEST AND RESULTS
In this section, we present some results from
different tests carried out in our feedback ANC
system, with the characteristics explained in the
precedent section. All tests were carried out with
narrow band noise and they were grouped in two
types:
(a) Performance of the NFXLMS-NA algorithm,
from 150 to 550 Hz, at 15 seconds (Fig. 14). In the
figure, upper line shows the original noise; bottom
line shows the attenuated noise.
(b) Cancellation at select frequencies, from 0 to
15 seconds (Fig. 15(a), (b) and (c)).
Figure 16 shows the frequency view of the
cancellation of the (175 Hz + 275 Hz) signal
For Figs 15(a), (b) and (c), the horizontal axis
are values of 100 averaged samples (125
microseconds sample rate) for a total of 15 seconds.
The vertical axis is the amplitude expressed in
decibels (dB´s).
IMPROVED STABLE FEEDBACK ANC SYSTEM WITH DYNAMIC SECONDARY PATH MODELING
197

Figure 14: Performance of the NFXLMS-NA algorithm
Figure 15(a)
Figure 15(b)
Figure 15(c)
Figure 15: Cancellation at select frequencies (a) 200 Hz,
(b) 350 Hz and (c) 175 Hz + 275 Hz
Figure 16: Cancellation at frequencies 175 Hz + 275 Hz
(frequency. view, second 15)
5 CONCLUDING REMARKS
We proposed a new algorithm (NFXLMS-NA) in
order to get a better stability than the FXLMS
algorithm for ANC feedback systems. Experimental
results show that this the proposed ANC feedback
system attenuates narrow band noise just like a
feedforward system; however, this system has not
problem with acoustic feedback, because it works
without a external reference signal. Also, dynamic
tests showed that the on-line modeling of the
secondary path is a source of instability; but the
noise addition in the system makes it stable (the time
for all test were 60 seconds; here, 15 seconds test are
showed).
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
198

Finally, in Figs 14 and 15 we can see that some
of the most relevant results are: (a) the system has a
good performance besides the on-line modeling, (b)
narrow band noise is attenuated at least 7 dB´s in
open environments, (c) the system is stable and (d)
decorrelated broadband signals could be recovered
from narrow band noise; this last result was recorded
in an acoustic form.
REFERENCES
Bernard Widrow, J. Glover, J. McCool, Adaptive Noise
Cancelling: Principles and Applications, Proceedings
of IEEE, vol. 63, no 12, pp 1692-1716, Dec. 1975.
S. Kuo and D. Morgan, Active Noise Control Systems:
Algorithms and DSP implementations, New York,
N.Y.: John Wiley, 1996.
Stephen Elliot, Signal Processing for Active Control,
Academic Press, 2001.
B. Farhang-Boroujeny, Adaptive Filters: Theory and
Applications (Baffins Lane,Chichester: John Wiley,
1998)
S. Haykin, Adaptive Filter Theory, Upper Saddle River,
New Jersey: Prentice Hall, 1996 .
Victor Solo, Xuan Kong, Adaptive Signal Processing
Algorithms: Stability and Performance, Englewood
Cliffs, New Jersey, 1995.
Bustamante, R., H. M. Perez, Development and
Simulation of Active Noise Control Systems,
Proceedings of the 2002 International Symposium on
Active Control of Sound and Vibration, Southampton,
U.K., July 2002, pp 793-802.
Bustamante, R., H. M. Perez-Meana, and B. Psenicka,
Development, Simulation and Comparison of
Orhtogonalized LMS Algorithms for Active Noise
Control, in the International Technological Journal
Electromagnetic Waves and Electronic Systems,
Moscow, Russia, pp. 43-49, T.8, No. 7-8, 2003, ISSN
1560-4128
Rafaely, B., Elliot S. An adaptive robust feedback
controller for active control sound and vibration,
PUKACC International Conference on CONTROL´96,
IEE 1996, 2-5 September 1996, Conference
publication No. 427.
Zhang, M., Lan, H. and Ser W. Cross-update Active Noise
Control System with Online Secondary Path
Modeling, IEEE Transactions on speech and audio
processing. Vol. 9 No. 5, July 2001
.
IMPROVED STABLE FEEDBACK ANC SYSTEM WITH DYNAMIC SECONDARY PATH MODELING
199