IMPROVEMENT OF THE DYNAMICS OF THE CONTINUOUS
LINEAR SYSTEMS WITH CONSTRAINTS CONTROL
N.H. Mejhed +, A. Hmamed * and A. Benzaouia**
+ Dépt GII, ENSA , BP 33/S, Agadir, Morocco
* LESSI Département de physique, Faculté des sciences, B.P. 1796, 30 000, FES-Atlas, Morocco
** Université Cadi Ayad, Faculté des Sciences Semlalia, Département de Physique, B.P: 2390 Marrakech, Morroco
Keywords: Constrained control; Positively invariant sets; Time varying regulator; Lyapunov function; Extended
eigenvalues; Extended eigenvectors; x-eigenpair.
Abstract: In this work, A time varying control law is proposed for linear continuous-time systems with non
Symmetrical constrained control. Necessary and sufficient conditions allowing us to obtain the largest non-
symmetrical positively invariant polyhedral set with respect to (w.r.t) the system in the closed loop are
given. The asymptotic stability of the origin is also guaranteed. The case of symmetrical constrained control
is obtained as a particular case. The performances of our regulator with respect to the results of (Benzaouia
and Baddou, 1999) are shown with the help of an example.
1 INTRODUCTION
This paper is devoted to the study of linear
continuous-time systems described by (1):
n
x ),t(Bu)t(Ax)t(x ℜ∈+=

(1)
x is the state vector and u is the constrained control,
that is:
nm ,u
m
≤ℜ⊂Ω∈ (2)
Matrices A and B are constant and satisfy
assumption (3):
)B,A( Controllable (3)
Ω is the set of admissible controls defined by (4):
⎭
⎬
⎫
⎩
⎨
⎧
ℜ∈≤≤−ℜ∈=Ω
+
m
2112
m
intq,q ;quq/u (4)
This is a non-symmetrical polyhedral set, as is
generally the case in practical situation.
Practical control systems are often subject to
technological and safety constraints, which are
translated as bounds on the constraint and state
variables. The respect of this constraint can be
accomplished by designing suitable feedback law.
In many cases, this can be done by constructing
positively invariant domains inside the set of the
constraints. The purpose of a regulation law is to
stabilise the system while maintaining its state
vector in a positively invariant set (Benzaouia and
Hmamed, 1993) (Benzaouia and Burgat, 1989).
Many approaches have been derived from this
concept. Particularly, one which consists on both,
using large initialisation domain and respecting the
constrained control, (Benzaouia and Baddou, 1999)
(Benzaouia and Burgat, 1989) (Benzaoiua, 1988)
(Bistoris, 1991) (Wredenhagen and Bélanger, 1994).
Recently, a piecewise linear control law has been
derived for linear continuous time systems, leading
to the use of non-symmetrical Lyapunov functions
(Benzaouia and Baddou, 1999). These functions
were introduced in (Benzaouia and Burgat, 1989),
and are also used in (Benzaouia and Hmamed,
1993). Otherwise, the proposed technique seems to
be very long and the problem appears between the
size of the initialisation do main and the dynamic of
the closed loop system. This justifies the
development of this technique by using a time
varying regulator. The choose of such regulator has
been the subject of many works from which we cite,
(Makoudi and Radouane, 1992) (Makoudi and
Radouane, 1991) (Anderson and Moore, 1981) in the
decentralized control case. Inspired by the work in
(Benzaouia and Baddou, 1999), our contribution in
the present paper is intended to improve the speed of
regulation by setting the modified control law as
follows:
)t(x)t(F)t(xF)t()t(u
0
=φ= ,
mxn
0
F ℜ∈ (5)
m)F(rang
0
= with
0)t( >
φ
, 0t ≥∀ .
Taking into account (5), system (1) becomes a non-
stationary system in the following form:
215
H. Mejhed N., Hmamed A. and Benzaouia A. (2005).
IMPROVEMENT OF THE DYNAMICS OF THE CONTINUOUS LINEAR SYSTEMS WITH CONSTRAINTS CONTROL.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 215-224
DOI: 10.5220/0001163302150224
Copyright
c
 SciTePress

)t(x)BF)t(A()t(x
0
φ+=

, 0t ≥∀ (6)
Generally )t(
φ and matrix
0
F must be found that
makes the system (6) asymptotically stable and
inside the constraints. It is well known that a linear
time invariant system is stable if and only if ail
eigenvalues of the system matrix have negative real
parts (Hahn, 1967). However, this is no longer true
for linear time-varying systems. Under the
assumption of the non-stationary systems, the
eigenvalues method for proving the asymptotic
stability is not adequate. An alternative method is
the use of matrix measure that means:
ξ−≤φ+µ )BF)t(A(
0
, 0t ≥∀ ,
0≤
ξ
(7)
We will show latter in this work, how to choose the
function )t(φ .
Remark: Note that m))t(F(rang = , because
m)F(rang
0
= and 0)t( ≠φ , 0t ≥∀ .
In the constrained case, we follow the approach
proposed in (Gutman and Hagander, 1985) and
further developed in (Benzaouia and Hmamed,
1993) (Benzaouia and Burgat, 1989) and (Vassilaki
and Bistoris, 1989) and references therein. This
approach consists of giving conditions on the
choice of the stabilizing regulator (5) such that
model (6) remains valid. This is only possible if the
state is constrained to evolve in a specified region
defined by:
⎭
⎬
⎫
⎩
⎨
⎧
ℜ∈≤≤−ℜ∈=
+
m
2112
n
21
intq,q ;q)t(x)t(Fq/x)q,q),t(F(D
(8)
Note that this domain is unbounded where
n
m
< .
In this case, if
)q,q),t(F(D)t(x
21
∈ we may get
)q,q),t(F(D)t(x
21
∈λ+ , 0 ≥λ∀ . Note that the
main property of this set in the stationary case is not
valid in our case that is the set )q,q),t(F(D)t(x
21
∈ .
In particular, domain )q,q,I(D
21m
can be described
with function
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−+
i
2
i
i
1
i
i
q
z
,
q
z
maxmax)z(v (9)
i.e.,
⎭
⎬
⎫
⎩
⎨
⎧
≤ℜ∈= 1)z(v/z)q,q,I(D
m
21m
.
It follows from above that the main result of this
note is to give the necessary and sufficient
conditions under which the nonsymmetrical
polyhedral domain Ω is positively invariant w.r.t.
motions of system 6.
2 PRELIMINARIES
In this section, we present some definitions and
useful results for the sequel. Consider a continuous-
time non-linear system
0)0(f,z )),t(z(f)t(z
m
=ℜ∈=

(10)
Definitions 2.1: i) Consider a function
+
ℜ→ℜ
m
:v with 0)0(v = and assume that v is
directionally differentiable at each direction and
define
)z(v

by:
[][ ] ))t(z(f);t(zv))t(z(v
dt
d
))t(z(v ∂==
+

ε
−ε+
=
+
→ε
)z(v))z(fz(v
lim
0
(11)
)z(v

is the directional derivative of function v at z
in the direction f(z) (Hahn, 1967), with
0)0(f =
and
))t(z(f)t(z =

. ii) If function v is a Lyapunov
function of system (10) on a set
m
ℜ⊆ℑ then
domain D defined by
{} 0c,c)z(v/zD >≤ℑ∈=
is a stability domain of the system.
Lemma 2.2 (Desoer and Vidyasagar, 1975):
Let A,
nxn
CB ∈ , we have:
a) n,...,1i),A())A(Re(
i
=∀µ≤λ .
b) 0c),A(c)cA( ≥∀µ=µ
c)
c)A()cIA( +
µ
=+
µ
, ℜ∈∀c
d)
)B()A()BA(
µ
+
µ
≤+
µ
e)
ℜ→µ
nxn
C: is convex on
nxn
C
),B()1()A()B)1(A(
µ
λ−+λ
µ
≤λ−+λ
µ
]1,0[∈λ∀
Definition 2.3 (Benzaoiua, 1988):
A differentiable
non-zeros vector e(t) is said to be the extended-
eigenvector (x-eigenpair) of the nxn matrix G(t),
associated with the extended-eigenvalues )t(λ (a
scalar time function) if it satisfies,
)t(e)t(e)t()t(e)t(G

+λ=
Consider the following continuous non-stationary
system,
)t(z)t(H)t(z =

,
m
z ℜ⊆ℑ∈ and ℑ∈ Int0 (12)
The necessary and sufficient condition of function v
defined by (9) to be a Lyapunov function for system
(12) is given by the following result.
ICINCO 2005 - ROBOTICS AND AUTOMATION
216

Theorem 2.4
Function
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−+
i
2
i
i
1
i
i
q
z
,
q
z
maxmax)z(v with
0q ,0q
21
>> , which is continuous positive
definite, is a Lyapunov function of system (12) on
the set ℑ and domain:
ℑ⊆
⎭
⎬
⎫
⎩
⎨
⎧
≤≤−ℜ∈=
12
m
21m
qzq/z)q,q,I(D
is a stability domain of the system if and only if :
0q)t(H
~
≤ , 0t ≥∀ (13)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
)
12
21
t()t(
)t()t(
HH
HH
)t(H
~
,
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
2
1
q
q
q, 0t ≥∀
ji (t)h
ji (t)h
)t(H
ij
ii
1
⎪
⎩
⎪
⎨
⎧
≠
=
=
+
,
⎪
⎩
⎪
⎨
⎧
≠
=
=
−
ji (t)h
ji 0
)t(H
ij
2
Proof: (If) The same as (Benzaouia and Hmamed,
1993), with:
()()
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
++
≤ )z(v
q
q)t(Hq)t(H
);z(v
q
q)t(Hq)t(H
maxmax)z(v
i
2
i
2112
i
1
i
2211
i

0t ≥∀ (14)
From condition (13), we have:
0)z(v ≤

,
m
z ℜ⊆ℑ∈∀
Consequently, from (Hahn, 1967), we conclude that
domain )q,q,I(D
21m
is a stability domain of the
system.
(Only if): Assume that function )z(v is a Lyapunov
function of system (6) and condition (13) does not
hold, i.e., there exist only
]m,1[i ∈ such that,
0q)t(hq)t(hq)t(h
m
ij,1j
j
2ij
j
1ij
i
1ii
>
⎥
⎦
⎤
⎢
⎣
⎡
++
∑
≠=
−+
At this step, we follow the proof given in
(Benzaouia and Hmamed, 1993).
Remarks
1)
When 1)t( =φ , we obtain the result given in
(Benzaouia and Hmamed, 1993).
2) It is well known that a stability domain for system
(12) is also a positively set for the system
3) The relation (13) is equivalent to the following
matrix measure:
0))t(H( ≤µ , 0t ≥∀ (15)
Induced by the vector norm:
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
−+
i
2
i
i
1
i
i
q
z
,
q
z
maxmaxz (16)
For more detail, see
Appendix 1.
4) If there exist
0>
ξ
such that ξ−≤µ ))t(H(, we
have:
)z(v)z(v ξ−≤

(17)
and then from (Hahn, 1967), system (12) is
asymptotically stable.
The symmetrical case is obtained directly by :
Corollary 2.5
Function
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
i
q
i
z
i
max)z(v is a Lyapunov
function of system (12) on the set
ℑ and domain
ℑ⊆
⎭
⎬
⎫
⎩
⎨
⎧
≤≤−ℜ∈= qzq/z)q,q,I(D
m
m
is a
stability domain of the system if and only if:
0q)t(H
ˆ
≤ with
⎪
⎩
⎪
⎨
⎧
≠
=
=
ji )t(h
ji )t(h
H
ˆ
ij
ii
, 0t ≥∀
Proof: Follows readily from Theorem 2.4.
3 MAIN RESULTS
In this section, we apply the results of Theorem 2.4
to the problem of the constrained regulator described
in Section I.
Consider system (1) with the feedback law given by
(5). The system in the closed loop is then given by
(6). Let us make the change of variables,
)t(xF)t()t(z
0
φ= ,
mxn
0
F ℜ∈ (18)
)t(x)t(F=
with matrix
0
F given by (5) and (7). It follows that:
[
]
)t(x)BF)t(A(F)t(F)t()t(z
000
φ+φ+φ=


)t(xBF)t(AI
)t(
)t(
F)t(
0n0
⎥
⎦
⎤
⎢
⎣
⎡
φ++
φ
φ
φ=

If there exists a matrix
mxm
)t(H ℜ∈ such that:
[] )t(F I
)t(
)t(
)t(H)t(BFA)t(F
n
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
−=+

, 0t ≥∀
(19)
Then, the change of variables (18) allows us to
transform dynamical system (6) to dynamical non-
stationary system (12). The study of the stability of
system (6) with )q,q),t(F(Dx
21
∈ defined by (8),
becomes possible by the use of system (12) and
Theorem 2.4, with Ω==ℑ∈ )q,q,I(Dz
21m
.
IMPROVEMENT OF THE DYNAMICS OF THE CONTINUOUS LINEAR SYSTEMS WITH CONSTRAINTS
CONTROL
217

Before giving the main result, we present all the
necessary Lemmas. The first concerns (19), which is
to be for every t.
For this, let us define the set
)F(ℵ
of the matrix F(t)
as follows :
⎭
⎬
⎫
⎩
⎨
⎧
ℜ∈≥∀=ℜ∈=ℵ
mxnn
F(t) 0,t 0,F(t)x(t) /)t(x)F(
I
n the stationary case, )F(Ker)F( =ℵ
We note )t(

n
I
)t(
)t(
)t(H
φ
φ
−=

and
)t(BFA)t(A
0
+= .
Lemma 3.1
If a matrix
mxm
)t(H ℜ∈ satisfying (19) exists, then
n-m stables extended eigenvectors common to
matrices
A
and )t(A
0
belong to
)F(ℵ
.
Proof:
Let a matrix )t( satisfying equation (19) exists.
Consider an extended eigenvector )t(e of matrix
)t(A
0
corresponding to an extended eigenvalue
)t(
λ , (Min-Yen, 1982), i.e:
)t(e)t(e)t()t(e)t(A
0

+λ= (20)
Equation (19) allows us to write
))t(e)t(F())t(e)t(F)(t()t(e)t(A)t(F
0

+λ= (21)
))t(e)t(F)(t(
=
Then )t(e)t(F is an extended eigenvector of matrix
)t(
 corresponding to the same extended eigenvalue
)t(
λ . Matrix
mxm
)t( ℜ∈ could admit only m
extended eigenvalues from the set of extended
eigenvalues of matrix )t(A
0
. Let us note
210
))t(A( Λ∪Λ=Λ=σ , with σ ()t( ) ⊂
m
C and
mn
2
C
−
⊂Λ .
Where ))t(A(
0
σ (
))t((σ
) denotes a set of extended
eigenvalues of )t(A
0
(respectively )t( ).
Then, for
2
Λ∈δ , we should have,
)t(w)t(w)t()t(w)t(A
0

+δ= (22)
then
))t(w)t(F()t(w)t(F)(t()t(w)t(A)t(F
0

+δ=
))t(w)t(F)(t(
= (23)
Implies,
0)t(w)t(F = ,
0
tt ≥∀ (24)
For w satisfying )t(w)t(w)t(w)t(A
0

+δ= .
Since )t(F)t(B)t(A)t(A
0
+= , we should also have:
)t(w)t(w)t()t(w)t(F)t(B)t(w)t(A

+δ=+
From (24), we obtain )t(w)t(w)t()t(w)t(A

+δ= ,
and then ))t(A(
2
σ⊂Λ .
If 0=δ , then from (23), 0))t(w)t(F)(dt/d( = ,
implies cste)t(w)t(F = . In this case, vector w(t) do
not belong necessarily to
)F(ℵ
. Further, condition
(7) ensures that
(
)
ξ−≤µ )t(A
0
,
0>
ξ
,
0
tt ≥∀ ,
using the fact that ))t(A())t(A(Re(
00i
µ≤λ ,
(Benzaouia, 1994), then, the set of extended
eigenvalues of matrix )t(A
0
is stable. Consequently,
2
Λ contains n-m stable and non-null extended
eigenvalues corresponding to n-m common extended
eigenvectors to matrices A(t) and )t(A
0
and
belonging to
)F(ℵ
.
We now give two lemmas on the
)F(ℵ
with
mxn
)t(F ℜ∈ and m))t(F(rank = .
Lemma 3.2
There exists a matrix
mxm
)t(H ℜ∈ satisfying
relation (19) if and only if the existence of 0t >
such that )F()t(x ℵ∈ implies )F()t(x ℵ∈τ+ ,
0>τ∀ , t∀ .
Proof: (If): Assume that there exists a matrix
mxm
)t(H ℜ∈ satisfying (19) and let )F()0(x ℵ∈ ,
that is,
0)0(x)0(F =
(25)
Let us present the solution for system (6) in the
following form,
0t),0(xe)t(x
t
0
0
d)BF)(A(
≥∀=
∫
ττφ+
(26)
Using the fact that,
∑
∫
∞
=
ττφ+
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
τφ+=
∫
0k
k
t
0
0
d)BF)(A(
d)BF)t(A(e
t
0
0
∑
∞
=
∫
⎭
⎬
⎫
⎩
⎨
⎧
τφ++=
1k
k
t
0
0
d)BF)t(A(I
By using (19) and the following relation obtained
from (19)
0
d)(HI
)(
)(
d)BF)(A(
0
FeeF
t
0
t
0
0
τ
⎥
⎦
⎤
⎢
⎣
⎡
τ+
τφ
τφ
−
ττφ+
∫
∫
=

ICINCO 2005 - ROBOTICS AND AUTOMATION
218

then,
)0(x)t(Fe)0(xe)t(F
0
d)(HI
)(
)(
d)BF)(A(
t
0
t
0
0
φ=
τ
⎥
⎦
⎤
⎢
⎣
⎡
τ+
τφ
τφ
−
ττφ+
∫
∫

By using (25) and the fact that 0t,0)t( ≥∀≠φ , we
obtain
0t,0)t(xF)t(
0
≥∀=φ , i.e., )F()t(x ℵ∈ , 0t ≥∀ .
(Only if): Assume that the existence of 0t > such
that )F()t(x ℵ∈ implies )F()t(x ℵ∈τ+ , 0>τ∀ ,
and show that condition (19) holds. Let, that is
0t,0)t(xF)t(
0
≥∀=φ . It is clear that
() 0))t(Fx(dt/d = and obviously
0t,0)t(xF)t()t(xF)t(
00
≥∀=φ+φ


.
We obtain:
⎪
⎩
⎪
⎨
⎧
=
⎥
⎦
⎤
⎢
⎣
⎡
φ++
φ
φ
=φ
0)t(xBF)t(AI
)t(
)t(
F
0)t(xF)t(
0
0

, 0t ≥∀ (27)
In this step, we can generalize the results of
(Benzaouia and Hmamed, 1993) to the relation (27).
This implies the existence of
mxm
)t(H ℜ∈ such
that (19) is satisfied.
Lemma 3.3
If domain )q,q),t(F(D
21
is positively invariant w.r.t.
system (6), 0t ≥∀ , then if )F()t(x ℵ∈ ,
)F()t(x ℵ∈τ+ , 0>τ∀ .
Proof: Let )F()0(x ℵ∈ , it is clear that
)q,q),t(F(D)0(x
21
∈ . From (26), we can deduce
)0(xe)t(F)t(x)t(F
t
0
0
d)BF)(A(
∫
ττφ+
= , 0>τ∀ .
At this step, we can use the proof given in
(Benzaouia and Hmamed, 1993) as the proof
remains unchanged. We can deduce that
0t,0)t(x)t(F ≥∀=
.
We are now able to give the main result of this
paper.
Theorem 3.4
Domain )q,q),t(F(D
21
is positively invariant w.r.t
system (6) if and only if there exists a matrix
mxm
)t(H ℜ∈ , such that:
i) []
0n00
FI
)t(
)t(
)t(HBF)t(AF
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
−=φ+

, 0t ≥∀
(
28)
ii) 0q)t(H
~
≤ , 0t ≥∀ (29)
with matrix )t(H
~
and vector q are defined by (13).
Proof: The proof is the same as given in (Benzaouia
and Hmamed, 1993) and is omitted for brevity.
Remark:
When 1)t( =φ , we obtain the result given in
(Benzaouia and Hmamed, 1993).
The symmetrical case is obtained directly by
Corollary3.5.
Corollary 3.5
If ρ==
21
qq , domain )q,q),t(F(D
21
is positively
invariant w.r.t system (6) if and only if there exists a
matrix
mxm
)t(H ℜ∈ , such that:
i) []
0n00
FI
)t(
)t(
)t(HBF)t(AF
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
−=φ+

, 0t ≥∀
ii) 0q)t(H
ˆ
≤ , 0t ≥∀ .
matrix
H
ˆ
is given in Corollary 2.4.
The result of this Theorem is based on the existence
of a matrix
mxm
)t(H ℜ∈ satisfying (19). A
necessary and sufficient condition of the existence of
a matrix )t(H is giving by the following Theorem.
Theorem 3.6
There exists a matrix
mxm
)t(H ℜ∈ solution of (19)
or (28), where
m
0
F ℜ∈ and m)F(rang
0
= ,
n
m
≤
if and only if :
m
AF
F
rang
0
0
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
(30)
Proof: We change only matrix A by
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
φ
φ
AI
)t(
)t(

in the proof given in (Porter, 1977) and by observing
that:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
φ
φ
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
φ
φ
AF
F
II
)t(
)t(
0I
AI
)t(
)t(
F
F
0
0
0
0


The proof remains unchanged.
In order to ensure a rate of increase of the system
dynamics, one should impose to matrix H(t) :
0t , qq)t(H
~
≥∀ε−≤
where ε is a positive real number ( 0≥ε ).
Comments
Conditions (28) and (29) guarantee that domain
)q,q),t(F(D
21
defined by (8) is positively invariant
w.r.t system (1)-(7), despite the existence of non-
symmetrical constraints on the control, but these
IMPROVEMENT OF THE DYNAMICS OF THE CONTINUOUS LINEAR SYSTEMS WITH CONSTRAINTS
CONTROL
219

conditions are very difficult to verify, because we
can not compute the matrix
)t(H
for all t. Then, we
propose to employ only
)0(H
and
)(H ∞
to handle
such situation.
Before proving the Proposition 3.7, we first need the
following assumptions about the function )t(φ :
(a)
0)t( >
φ
, 0t ≥∀
(b) )t(φ is a nondecreasing function.
(c)
⎟
⎠
⎞
⎜
⎝
⎛
∞φ−φ
∞φ−φ
φ
φ
≤
φ
φ
)()0(
)()t(
)0(
)0(
)t(
)t(

, 0t ≥∀ .
Remarks
1) From assumption (a) and (b), we have:
)()t()0(0 ∞φ≤φ≤φ< , 0t ≥∀
It follows that,
1
)()0(
)()t(
0 ≤
∞φ−φ
∞φ−φ
≤ , 0t ≥∀
2) From (b), we have 0)t( ≥φ

, 0t ≥∀ , then from
(a), we can conclude that:
0
)t(
)t(
≥
φ
φ

, 0t ≥∀
3) Giving the inequality (c), and taking its limit as t
tends to infinity, one has:
⎟
⎠
⎞
⎜
⎝
⎛
∞φ−φ
∞φ−φ
φ
φ
≤
φ
φ
∞→∞→
)()0(
)()t(
)0(
)0(
lim
)t(
)t(
lim
tt

It is clear that: 0
)(
)(
≤
∞φ
∞φ

, 0t ≥∀ .
Combining this condition and the condition giving
by Remark2, (i.e.
0
)t(
)t(
≥
φ
φ

, 0t ≥∀ ), this implies
that:
0
)(
)(
=
∞φ
∞φ

. From assumption (a), one has
0)( =∞φ

. This suffices to conclude that:
Kcste)( ==∞φ .
Proposition 3.7
The polyhedral set defined by (8) is a positively
invariant w.r.t. system (6) if and only if there exists
)0(H
and
)(H ∞
such that:
[]
0n00
FI
)0(
)0(
)0(HBF)0(AF
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
−=φ+

(31)
[]
0n00
FI
)(
)(
)(HBF)(AF
⎥
⎦
⎤
⎢
⎣
⎡
∞φ
∞φ
−∞=∞φ+

(32)
0q)0(H
~
≤ (33)
0q)(H
~
≤∞ (34)
Proof:
(IF)
It follows from (31), (32) and (19) that:
⎥
⎦
⎤
⎢
⎣
⎡
φ+
φ
φ
−=
0m000
BF)0(I
)0(
)0(
FF)0(HAF

(35)
⎥
⎦
⎤
⎢
⎣
⎡
∞φ+
∞φ
∞φ
−∞=
0m00
BF)(I
)(
)(
FF)(H

(36)
⎥
⎦
⎤
⎢
⎣
⎡
φ+
φ
φ
−=
0m00
BF)t(I
)t(
)t(
FF)t(H

(37)
Then the full rankness of the matrix
0
F leads to the
following equation,
BF)0(I
)0(
)0(
)0(HBF)(I
)(
)(
)(H
00
φ−
φ
φ
−=∞φ−
∞φ
∞φ
−∞

(38)
Then,
[] BF )()0(I
)(
)(
)0(
)0(
)0(H)(H
0
∞φ−φ−
⎥
⎦
⎤
⎢
⎣
⎡
∞φ
∞φ
−
φ
φ
−=∞

(
39)
From (37) and (38), we have:
)0(H
)()0(
)()t(
)(H
)()0(
)()t(
1)t(H
⎟
⎠
⎞
⎜
⎝
⎛
∞φ−φ
∞φ−φ
+∞
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∞φ−φ
∞φ−φ
−=
m
I
)0(
)0(
)()0(
)()t(
)(
)(
)()0(
)()t(
1
)t(
)t(
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
⎟
⎠
⎞
⎜
⎝
⎛
∞φ−φ
∞φ−φ
−
∞φ
∞φ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∞φ−φ
∞φ−φ
−−
φ
φ
+

(40)
We note:
)()0(
)()t(
)t(e
∞φ−φ
∞φ−φ
= (41)
Then,
() )I)t( c)0(eH)(H)t(e1())t(H(
m
++∞−
µ
=
µ
(42)
where:
() 0
)0(
)0(
)t(e
)(
)(
)t(e1
)t(
)t(
)t( c ≤
φ
φ
−
∞φ
∞φ
−−
φ
φ
=

(43)
and e(t) is giving by (41).
By applying Lemma 2.2 ©, we have,
() )t(c))0(H)t(e)(H)t(e1())t(H( ++∞−µ=µ (44)
)t(φ is chosen to satisfy (a), (b) and (c), then by
applying Lemma 2.2 to equation (44), we obtain,
() c(t) ))0(H()t(e))(H()t(e1))t(H( +µ+∞µ−≤µ (45)
where c(t) is giving by (40) and e(t) by (41).
Furthermore,
)t(c))(H(),0(H(max())t(H( +∞
µ
µ
≤
µ
,0)t(c ≤ (46)
It follows that if (33) and (34) holds, from the above
results, one should obtain 0q)t(H
~
≤ , 0t ≥∀ .
(Only if): We assume that the polyhedral (8) is
positively invariant w.r.t. system (6). By using
Theorem3.4, there exists
mxm
)t(H ℜ∈ such that:
ICINCO 2005 - ROBOTICS AND AUTOMATION
220

[]
0n00
FI
)t(
)t(
)t(HBF)t(AF
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
−=φ+

0t 0q)t(H
~
≥∀≤
In particular, for 0t = and ∞→t , we obtain:
[]
0n00
FI
)0(
)0(
)0(HBF)0(AF
⎥
⎦
⎤
⎢
⎣
⎡
φ
φ
−=φ+

[]
0n00
FI
)(
)(
)(HBF)(AF
⎥
⎦
⎤
⎢
⎣
⎡
∞φ
∞φ
−∞=∞φ+

0q)0(H
~
≤
0q)(H
~
≤∞
Remarks
1) The symmetrical case is easily deduced.
2) In order to augment the system dynamics, one
should impose to matrices
)0(H
and
)(H ∞
:
qq)0(H
~
ε−≤ (47)
qq)(H
~
ε−≤∞ (48)
where ε is a positive number 0≥ε .
Comments:
When the regulator
0
F is changed to
0
F)(F ∞φ=
∞
,
the eigenvalues of
)(H ∞
will be placed in a region
of the left half-complex space, which makes them
more stables than the eigenvalues of
)0(H
.
Furthermore, the control law increases the gain as
the trajectory converges towards the origin.
)t(φ is chosen to satisfy assumptions (a), (b) and (c).
This means that the dynamics amelioration cannot
be made with enough liberty.
4 APPLICATION
The assumption (a), (b) and (c) institute the class of
regulator, which permit to achieve the desired
performance. In particular, we can choose )t(φ in
the form:
)e1(1)t(
tα−
−β+=φ ,
0, ≥
β
α
It is clear that the assumption a)-c) are satisfied.
The aim of this kind of regulator is to permit to start
with a slow dynamics very close to the regulator
with the gain
0
F and to force this dynamics to
increase until it reaches the one of the regulator with
the gain
0
F)1( β+ at asymptotic behaviour. In
addition, this permits the boundless of the time-
varying control gain
)t(
φ
.
In this case, equation (31) and (32) become the
following:
0m00
FI)0(H)BFA(F
⎥
⎦
⎤
⎢
⎣
⎡
αβ−=+
000
F)(H]BF)1(A[F ∞=β++
with :
I )0(He)(H)e1()t(H
tt α−α−
+∞−=
I e
)e1(1
e
t
t
t
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
αβ−
−β+
αβ
+
α−
α−
α−
and
BFI)(H)0(H
0
β−αβ+∞=
Two parameters must be found to satisfy assumption
(a), (b) and (c) with:
)e1(1
e
)t(
)t(
t
t
α−
α−
−β+
αβ
=
φ
φ

, αβ=
φ
φ
)0(
)0(

, 0
)(
)(
=
∞φ
∞φ

.
From (45), we have:
I ))0(H(e))(H()e1())t(H(
tt
µ+∞µ−≤µ
α−α−
)e1(1
)e1(e
-
t
tt2
α−
α−α−
−β+
−αβ
, 0t ≥∀
In order to recapitulate all the steps required to
satisfy our purpose, we present the following
algorithm.
Algorithm
Step0: Verify that A possesses (n-m) stable
eigenvalues. When it is not the case, we proceed to
an augmentation of the vector entries without losing
assumption (3a), this technique is given in
(Benzaouia and Burgat, 1989 - a).
Step1: Give ε ,
0 , ≥
β
α
and a matrix H(0) such
that;
qq)0(H
~
ε−≤
Step2: Solve equation (31) by using the inverse
procedure detailed in (Benzaouia, 1994) to obtain
0
F.
Step3: Solve equation (32) to obtain
)(H ∞
.
Step4: If qq)(H
~
ε−≤∞ holds, then use
α
,
β
and
0
F to realize a time-varying regulator. If not, we
return to step1.
5 COMPUTER SIMULATION
In this section, we present several numerical
examples illustrating the performance of the
IMPROVEMENT OF THE DYNAMICS OF THE CONTINUOUS LINEAR SYSTEMS WITH CONSTRAINTS
CONTROL
221

proposed regulator.
Example1
Consider the second order system (1) given by:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−
−
=
1
1
B ;
5.03
21
A ,
[]
T
513q = .
{} 8117.2,3120.2)A( −=σ
We choose, 21.0=
α
, 3=
β
and 3.0=ε and let:
39.0)0(H −=
.
The resolution of equation (31) gives:
[] 8422.5674.9F
0
−=
and then :
[] 36.2369.38F)1(F
0
−=β+=
∞
According to (32),
)(H ∞
is given
by:
4554.12)(H −=∞
and
[] q2770.629202.161q)(H
~
T
ε−≤−−=∞
We obtain the desired results given by:
{}
9998.0,3120.2)BFA(
0
−−=+
σ
{}
0358.11,3120.2)BF))e1(1(A(
10t0
t
−−=−β++σ
=
α−
{} 5152.12,3120.2)BFA( −−=+σ
∞
Note that the eigenvalues -2.3120 is common to A
and
0
BFA +
According to the result given in (Benzaouia and
Baddou, 1999), we choose N=3 and
0
H such that
00000
FHBFFAF =+ and qqH
~
0
ε−≤ , which
implies from (31) that 02.1I)0(HH
0
−=αβ−= .
From (Benzaouia and Baddou, 1999), if we choose
01.1
]3[
=α , we obtain the following results, with:
{} 3120.2,9998.0)BFA(
0
−−=+σ
{} 312.2, 0581.1)BF)(A(
0]3[
−−=α+σ .
{} 3120.2, 0968.1)BF)(A(
0
2
]3[
−−=α+σ .
{} 312.2, 1359.1 )BF)(A(
0
3
]3[
−−=α+σ .
Finally, the dynamics amelioration is guaranteed by
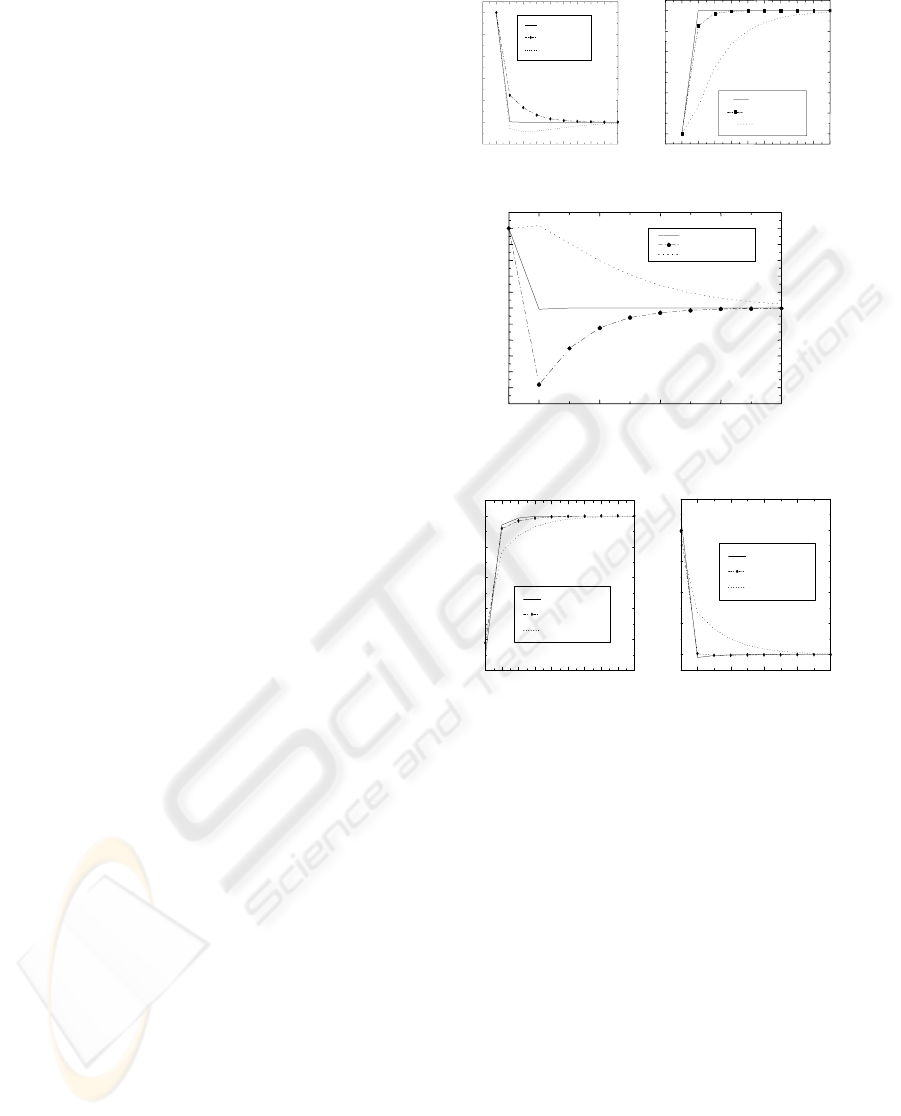
the choice of this regulator. The state and the control
components for time varying control, piece-wise
control (Benzaouia and Baddou, 1999) and for a
fixed gain chosen to be
0
F , the initial gain is
represented in figure4 and figure5 respectively.
2 4 6 8
10
-
0, 6
-
0, 4
-
0, 2
0, 0
0, 2
0, 4
0, 6
Trajectory of x1
Piece wise control
Initial gain F0
Time varying regulator
Ti me
2 4 6 8 10
-
0,1
0,
0
0,
1
0,
2
0,
3
0,
4
0,
5
0,
6
0,
7
0,
8
0,
9
1,
0
1,
1
Piecewise
regulation
gain
initial F0
régulateur
variable
Trajectory of x2
Time
Figure 4: Space state
2 4 6 8 10
0
2
4
6
8
10
12
14
Trajectory of u
Piecewise control
Initial gain F0
Time varying regulator
Time
Figure 5: Control evolution
Example2
Consider the system (1) with:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−−
=
5.00
13.0
2.01
B ,
159.02
4445.0
321
A
Matrix A is unstable,
i.e,
{} 7983.3 ,2937.14 ,5046.1)A( −=σ .
[]
T
78.252637q = .
We choose 1.0=
α
and
2=
β
.
Let:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
=
3.00
04.0
)0(H
By applying the algorithm, the resolution of
equation (31) gives:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−−
=
0186.317706.19817.3
4774.179614.15443.4
F
0
and
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−−
=β+=
∞
0558.933118.59451.11
4322.528842.56329.13
F)1(F
0
If we choose 1.0=ε , according to (32), we obtain:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
=∞
3847.269010.6
7369.115118.8
)(H
ICINCO 2005 - ROBOTICS AND AUTOMATION
222

With : {} 1312.30,7653.4))(H( −−=∞σ and :
[]
q
6471.64461.1376652.430772.9q)(H
~
T
ε−≤
−−−−=∞
Finally, we obtain the following results:
{}
{}
{}
.7984.3,7653.4,1312.30)BF)1(A(
.7984.3,2275.3,2358.19)BF))e1(1(A(
.7984.3,5.0,6.0)BFA(
0
10t0
t
0
−−−=β++σ
−−−=−β++σ
−−−=+σ
=
α−
Note that -3.7984 is a common eigenvalues of A,
0
BFA + and
0
BF)1(A β++ .
Furthermore,
))0(H(Re())(H(Re(
ii
λ≤∞λ , m,,1i …=
Which means that in the control, the dominant
eigenvalues of
)(H ∞
is more stable than the
eigenvalues of
)0(H
.
According to the result given in (Benzaouia and
Baddou, 1999), we choose 3N = and a diagonal
matrix
0
H such that
00000
FHBFFAF =+ and
qqH
~
0
ε−≤ , which implies from (31) that:
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
−
=αβ−=
5.00
06.0
I)0(HH
0
From (Benzaouia and Baddou, 1999), we obtain
0260.10
]3[
≤α< , if we choose 025.1
]3[
=α , we
obtain the following results, with:
{} 7984.3,5.0,6.0)BFA(
0
−−−=+σ
{} 7983.3,9117.0,6361.0)BF)(A(
0]3[
−−−=α+σ .
{} 7983.3,3119.1,6955.0)BF)(A(
0
2
]3[
−−−=α+σ
{} 7983.3,7247.1,7546.0)BF)(A(
0
3
]3[
−−−=α+σ
Then, compared to the results given in (Benzaouia
and Baddou, 1999), the dynamics amelioration with
a time-varying regu1ator is guaranteed and is better
than that derived in (Benzaouia and Baddou, 1999).
The state and the control components for time
varying control, piece-wise contro1 (Benzaouia and
Baddou, 1999) and for a fixed gain chosen to be
0
F,
the initial gain is represented in figure2 and figure3
respectively.
0 1 2 3 4 5 6 7 8 9 10
-
0,5
0,0
0,5
1,0
1,5
2,0
2,5
Traject ory of x(1,t )
Time varying reg
Piece wise cont rol
Initial gain
Ti me
0 1 2 3 4 5 6 7 8 9 10
-3,0
-2,5
-2,0
-1,5
-1,0
-0,5
0,0
Traject ory of x(2,t)
Time varying reg
Piece wise regul at or
Initial gain F0
Ti me
2 4 6 8 10
-0,12
-0,10
-0,08
-0,06
-0,04
-0,02
0,00
0,02
0,04
0,06
0,08
0,10
0,12
Time varying
regulator
Piece wise control
[3]
Initial gain
F0
Time
Figure 2: Space state
12345678910
-25
-20
-15
-10
-5
0
Trajectoire de u(1,t )
régulateur variable
régulat ion par morceaux
gain initial F0
Temps
246810
0
5
10
15
20
25
Trajectoire de u(2, t)
régulat eur vari able
régulat ion par morceaux
gai n initial gain F0
Te mps
Figure 3: Control Evolution
6 CONCLUSION
In this paper, a time varying regulator is derived
for linear continuous time systems. Necessary and
sufficient conditions for domain )q,q),t(F(D
21
to
be a positively invariant set w.r.t. system (6) are
given. The proposed technique guarantees the
admissibility of the control and enables system in
the closed loop to admit the largest non-
symmetrical constrained control. The asymptotic
stability of the origin is also guaranteed. The
results have been shown to be better than the
literature ones.
REFERENCES
Benzaouia A. and A. Hmamed, (a)" Regulator problem for
IMPROVEMENT OF THE DYNAMICS OF THE CONTINUOUS LINEAR SYSTEMS WITH CONSTRAINTS
CONTROL
223

Linear continuous time systems with nonsymmetrical
constrained control using non-symmetrical Lyapunov
function," In Proc.3th CDC IEEE-Arizona, 1992; (b
)"Regu1ator problem for continuous time systems with
nonsymmetrica1 constrained control, "IEEE
Trans.Aut. Control. vol.38, no10, pp 1556-1560,
October 1993.
Benzaouia A. and C. Burgat, (a)" Regu1ator problem for
linear discrete-time systems with nonsymmetrica1
constrained control", Int.J.cont, vo1.48, n06,pp.244-
245, 1988; (b)" Existence of nonsymmetrica1
Lyapunov functions for systems," Int.syst.Sci.,
vo120,pp 597-607, 1989; (c)" Existence of non-
symmetrical stable domains for linear systems," Linear
A1gebra Appl., vo1.l21,pp.217-231,1989.
Benzaouia A. and A. Baddou," Piecewise linear
constrained contro1 for continuous-time systems,"
IEEE Trans. Aut. Control, Vol. 44, no. 7, pp. 1477,
July, 1999.
Benzaoiua A.," Application du concept d'invariance
positive à l'étude des problèmes de commande des
systèmes dynamiques discrets avec contraintes sur la
commande". Thesis of UPS LAAS, No 88322, 1988.
Bistoris G.,"Existence of positively invariant polyhedral
sets for continuous time linear systems" Control theory
and advanced technology. voI.7,no3,ppA07-427,
September 1991.
Wredenhagen G.F. and P. R. Bélanger," Piecewise linear
LQ control for systems with input constraints,"
Automatica, vol.30, no3,pp. 403-416,1994.
Benzaouia A., "The resolution of equation XA+XBX=HX
and the pole assignment problem" IEEE. Trans.on
aut.Cont. vo1.39, nol0, pp2091-2094 ,October 1994.
B. Porter, "Eigenvalue assignment in linear multivariable
systems by output feedback," InU.contr.,voI.25, no.3,
ppA83-490, 1977.
W. Hahn, Stabilty of Motion, Berlin: Springer-Verlag,
1967.
P.O. Gutman and P.A. Hagander, "New design of
constrained controllers for liner systems," IEEE Trans.
Automat. Contr., vol. AC-30, pp. 22_23,
1985.
M. Vassilaki and G. Bistoris, "Constrained regulation of
linear continuous-time dynamical systems," Syst.
Contr. Lett., vol. 13, pp. 247-252, 1989.
C.A., Desoer and M. Vidyasagar, "Feedback Systems:
Input-Output Properties (New York: Academic Press),
1975.
Min-Yen Wu, " On stability of linear time-varying
systems", CDC-IEEE, pp. 1211-1214, 1982.
Makoudi M and Radouane L. (1992). On decentralized
discrete time varying feedback control. Advances in
modelling and analysis C, vol.33, NA, pp.29-38.
Makoudi M and Radouane L. (1991). On decentralized
time varying feedback control of linear continuous
systems. Troisième colloque magrébin sur les modèles
numériques de l'ingénieur. November, 26-29, Tunis.
Anderson B.O.D., Moore LB., 1981, "Time-varying
feedback laws for decentralised control", IEEE. Trans.
Autom. Control, vo1.26, N5, 11
33.
APPENDIX I
Matrix norm
∞
M
The matrix norm given by the vector norm:
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
−+
∞
i
2
i
i
1
i
i
q
z
,
q
z
maxmaxz
is giving by
∞
=
∞
∞
= Mz M
max
1z
then :
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
−+
∞
i
2
i
i
1
i
i
q
)Mz(
,
q
)Mz(
maxmaxMz
For this, we use the result of (Benzaouia and Burgat,
1989 – b, c)
∞
+−−+
∞
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
++
= z
q
)qM()qM(
,
q
)qM()qM(
maxmaxMz
i
2
i2i1
i
1
i2i1
i
Thus, =
∞
M
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
++
+−
∑
=
−+
∑
=
iji
2
j
2
ij
m
1j
i
2
j
1
iji
1
j
2
ij
m
1j
i
1
j
1
i
m
q
q
m
q
q
;m
q
q
m
q
q
maxmax
APPENDIX II
NOTATIONS: If x is a vector of
n
ℜ then:
)0,xsup( xand )0,xsup(x
i
-
iii
−==
+
, n,,1i …=
We will further note the following: for two vectors x, y of
n
ℜ :
yx ≤
(Respectively,
y
x
< ) if
ii
yx ≤ (respectively,
ii
yx < ) n,,1i …= .
n
I is the identity matrix of
nxn
ℜ ;
)A(σ
denotes the spectrum
of matrix A;
)Re(λ
the real part of the eigenvalue λ and
)A(
i
λ the ith eigenvalue of A.
)A(
µ
the measure of A ,
)(Int
m
+
ℜ is the interior of
m
+
ℜ , whereas D∂ denotes
the boundary of D.
F Ker is the null space of matrix F.
ICINCO 2005 - ROBOTICS AND AUTOMATION
224