INFORMATION-BASED INVERSE KINEMATCS MODELING

FOR ANIMATION AND ROBOTICS

Mikyung Kim and Mahmoud Tarokh

Department of Computer Science. San Diego State University, San Diego, CA 92124, U.S.A.

Keywords: Inverse kinematics, robotics, Neural networks, Animation.

Abstract: The paper proposes a novel method for extremely fast inverse kinematics computation suitable for

animation of anthropomorphic limbs, and fast moving lightweight manipulators. In the information

intensive preprocessing phase, the workspace of the robot is decomposed into small cells, and joint angle

vectors (configurations) and end-effector position/ orientation (posture) data sets are generated randomly in

each cell using the forward kinematics. Due to the existence of multiple solutions for a desired posture, the

generated configurations form clusters in the joint space which are classified. After the classification, the

data belonging to each solution is used to determine the parameters of simple polynomial or neural network

models that closely approximates the inverse kinematics within a cell. These parameters are stored in a

lookup file. During the online phase, given the desired posture, the index of the appropriate cell is found,

the model parameters are retrieved, and the joint angles are computed. The advantages of the proposed

method over the existing approaches are discussed in the paper. In particular, the method is complete

(provides all solutions), and is extremely fast. Statistical analyses for an industrial manipulator and an

anthropomorphic arm are provided using both polynomial and neural network inverse kinematics models,

which demonstrate the performance of the proposed method.

1 INTRODUCTION

One of the most fundamental and ever present

problems in computer animation and robotics is the

inverse kinematics (IK). This problem maybe posed

as follows: Given a desired posture vector u

representing the hand (end-effector) position and

orientation, and the forward kinematics equation

)(fu

= , find the set of all joint angle vectors

(configurations)

of the animation character or

manipulator that satisfy the forward kinematics

equation. The IK mapping is in general one to

many, involves complex inverse trigonometric

functions, and for most manipulators and animation

figures no closed form solution exists. In addition, in

computer animation, as well as in real-time

manipulator applications, extremely fast IK

computation is required.

The IK problem has attracted immense attention

and numerous solutions have been proposed,

including algebraic, Jacobian-based and

neural/genetic algorithms. In the algebraic based

approaches, a system of nonlinear polynomial

equations in the elements of

is solved either

symbolically or numerically using various methods

(Uicker 1984, Manchoa 1994, Zhao 1994, Tolani

2000). Algebraic methods are generally

computationally intensive and are not suitable for

applications such as animation that require

extremely fast solutions.

Jacobian based approaches (e.g. Whitney 1972,

Press 1988), formulate problem at the velocity

level, i.e.

)t()(J)t(u

θθ



where J(q) is the

Jacobian matrix of the manipulator. The equation is

solved for the joint rate vector

)t(



, which is then

integrated to obtain

. When the manipulator is

redundant, the Jacobian matrix becomes non-square,

and several approaches such as Jacobian pseudo-

inverse and Jacobian augmentation have been

proposed to resolve the redundancy (e.g. Klein

1983, Seraji 1993). One of the main difficulties with

the Jacobian based approaches is the singularity

problem where J(q) becomes rank deficient, which

can cause joint velocities (and acceleration/jerk) to

become unacceptably large. To ameliorate the

singularity problem, a number of methods have been

proposed (e.g. Chiacchio 1991, Chiaverini 1994,

Kim M. and Tarokh M. (2005).

INFORMATION-BASED INVERSE KINEMATCS MODELING FOR ANIMATION AND ROBOTICS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 76-84

DOI: 10.5220/0001164600760084

 SciTePress

Lloyd 2001), each requiring special considerations

to deal with singularities with the associated

computation overhead. More importantly, they are

not complete in the sense that they do not provide all

solutions (configurations) for a given posture.

More recently, neural networks and genetic

algorithms have been used for solving the inverse

kinematics problem (e.g. Dermata 1996, Nearchou

1998, Khwaja 1998, Chapelle 2001, De Lope 2003).

Neural network and genetic algorithm methods are

not complete and therefore generally find a

particular solution rather than all solutions. Neural

networks face problems for approximating multi-

valued functions. Genetic algorithms do not

guarantee the convergence to a desired solution, but

their major difficulty is that they require many

generations (iterations) to arrive at an approximate

solution and therefore are not suitable for real-time

applications.

The purpose of this paper is to propose a novel

approach for ultra fast IK solutions with few

limitations for 6-DOF manipulators, and 7-DOF

anthropomorphic limbs used in animation. Fast IK

techniques are needed for multiple limb animation

characters such as a human figure for variety of

applications such as motion capture. The IK

problem is solved in two phases, an off-line

information-based preprocessing phase and an on-

line rapid evaluation phase. Preprocessing consists

of spatial decomposition, classification, optimal data

generation and simple polynomial curve fitting, or

neural network approximation. This off-line

preprocessing phase is performed only once for a

limb or a manipulator, and can be used an infinite

number of times during on-line IK computation.

Because of the preprocessing, the on-line phase,

which finds various configurations for a desired

posture, is extremely fast.

2 SPATIAL DECOMPOSITION

In this section we discuss the forward kinematics

and spatial decomposition for 7-DOF limbs and

manipulators. All the developments of this and

subsequent section will naturally be valid for the

cases with fewer 7-DOF, as will be demonstrated in

Section 5.

A human-like figure, often used in animation

and graphics, consists of a number of limbs i.e. arms

and legs. An arm (leg) is generally modeled as a 7

DOF chain consisting of the shoulder (hip) and the

wrist (ankle) each as a 3 DOF spherical joint, and

the elbow (knee) as a single DOF revolute joint

(Tolani 2000). The human-like figure is often

decomposed into limbs with the torso as the

common or reference coordinate. In motion capture

applications, position and orientation of the shoulder

(hip) and hand (foot) of a live subject are measured

using sensors attached to the body. The position and

orientation are then used in conjunction with inverse

kinematics to find the joint angles of the limbs in

order to drive animation characters. It is also noted

that most redundant robot manipulators used in

applications or in research are also 7 DOF (Seraji

1993). Examples of these manipulators are the

space station RMS and K1207 manufactured by

Robotics Research arm. The latter has a joint and

links arrangements similar to limb, but it also has

offset at joints.

Consider the forward kinematics equation of a

limb

)(fu

(1)

where

is the 17

vector of joint angles that define

the limb configuration, and u is the

16 × vector of

the limb posture which defines the hand position

(e.g. x, y, z) and orientation (e.g. Euler angles

,, ). We refer to the 7-dimensional space

whose the coordinates are the joint angles as the

configuration space and to the 6-dimensional space

whose coordinates are position and orientation as the

posture space. Because the dimension of the

configuration space is more than that of posture

space, the anthropomorphic limb has redundancy.

In order to encode and exploit the redundancy,

we parameterize the solution space using a single

variable v. This variable is specified on-line to

explore different solutions and choose the one best

suited for the application on hand. Elbow

inclination in a 7-DOF anthropomorphic limb or in

the K1207 manipulator is an example of such a

variable. The elbow inclination is defined as the

angle of the rotation, about the shoulder-wrist line,

of the plane containing origins of shoulder, elbow

and wrist. The elbow inclination, referred to as

swivel angle in (Tolani 2000) and as arm angle in

(Seraji 1993), has been used to constrain a selected

point on the limb, to perform aiming of the end-

effector towards a target point, to keep the figure

balanced, etc. (Tolani 2000)

The elbow inclination v can be written as

)(gv

(2)

INFORMATION-BASED INVERSE KINEMATCS MODELING FOR ANIMATION AND ROBOTICS

where

)(g

is a kinematics function that relates the

joint angles to the elbow inclination mentioned. In

the limb, v is in fact a function of only the first four

joint angles. We now augment kinematics equation

(1) with the variable constraint equation (2) to

obtain

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

)(g

)(f

or )(hw

= (3)

The new posture is now the

17 × vector

)vu(w = , the forward kinematics function is

))(g)(f()(h

θθθ

= and (3) represents the

kinematics of a non-redundant limb. The result of

the kinematics constraint is an increase in the

dimension of the posture space from 6 to 7.

We now decompose the posture space into

small cells so that the IK can be approximated by

very simple expression in each cell. These 7-

dimensional cells have their axes representing

positions

,y,

, orientation angles

βα ,, (using a

suitable convention such as Euler angles), and v (e.g.

elbow inclination). The cell side lengths are

obtained by dividing the maximum ranges of each

quantity,

,,,v,z,y,x into a number of

divisions

N,,N,N

. Any valid limb posture

will be in one of the cells defined above. Higher

values of

N,,N,N

correspond to smaller size

(volume) cells and result in more cells, adding to the

off-line computation effort. However, smaller cell

sizes will require simpler mathematical models for

representing the cell inverse kinematics. These

simpler models in turn speed up the on-line

computation effort.

Once the posture space is decomposed into the

cells, we must generate data points for each cell. The

data consists of sets of configuration vectors

and

their associated postures vectors w. A large number

of configurations are generated by assigning random

values in the range of joints angles, and (3) is used

to determine their respective posture w. Each

generated posture is placed into its appropriate cell,

and when the number of postures in a cell reaches a

predetermined value

N , the next generated

posture that falls into that cell is discarded. The

generation continues until a certain percentage of the

cells have

postures. It is noted that many cells

may be outside the workspace in which case they

will not contain any postures, and some cells are on

the boundary or partially in the workspace in which

case they will contain fewer than

postures.

3 CLASSIFICATION

The generated cell configuration-posture data set

}w,{

cannot be used for modelling without further

processing. First, it is noted that there can be a

number of configurations (solutions) for a given

posture. The anthropomorphic limb has a spherical 3

DOF shoulder joint (

321

) which together with

the a single DOF elbow joint (

) can achieve a

desired wrist position/elbow inclination (sub-

posture) with a maximum of four sets of joint

angles (sub-configurations), namely,

(

4321

,,,

), (

4321

,,,

+ ),

(

4321

,,,

−

) and

(

4321

,,,

−

). It is noted that only

the first three angles are responsible for providing

different solution. In addition, the wrist is also a

spherical joint, and a desired hand orientation can be

achieved with two sets of wrist joint angles

765

. Thus the maximum number of solutions

(configurations) for a desired posture is eight. The

kinematics of the limb is such that the hand position

and elbow inclination

,y,

are dependent only

on the first four joint angles

,," . The wrist

angles

765

,, are dependent both on these four

joints and the desired orientation

,, .

Before cell IK modelling, configuration-posture

data belonging to a solution must be separated from

those of the other solutions within a cell. In (Tarokh

2005), we have developed a fuzzy classification

method to classify the solutions.

4 INVERSE KINEMATICS

MODELING

The purpose of this step in the preprocessing phase

is to develop a simple model for the IK, and to

determine its parameters for each solution within

each cell. The simplicity or complexity of the

required model depends on the size of the cell.

Smaller size cells will require simpler models to

accurately represent postures in them, but the

number of cells will be higher since the posture

space volume is constant. The opposite is true for

larger cell sizes, which require more complex

ICINCO 2005 - ROBOTICS AND AUTOMATION

models. For animation, high position/orientation

accuracy is not essential, but very short online

computation time is needed, and therefore a simple

model is preferred. We consider two models,

namely polynomial and neural network models as

follows:

4.1 Polynomial Model

The simplest polynomial model representing the

relationship between the first four joint angles and

position/inclination belonging to a particular

solution in a cell is the linear equation

ii i

a(xyzv) i 1,2, ,4

θσ

=+="

(4)

where

a is a 41× constant parameter vector and

σ is a constant scalar parameter. These parameters

are determined via a least squares (regression)

method for each cell using the cell data set. Note

that the same accuracy of the inverse kinematics

solution can be obtained by reducing the number of

cells but increasing the order of the model which in

turn increases the number of model parameters and

online computation time.

The model parameters are stored as records in a file

for the subsequent online retrieval. Each record has a

unique address in the file where the parameters of a

cell inverse kinematics model are stored. Suppose

there are D divisions for each of the axes

,y,

Then there will be

cell

DD= cells, and the file

address is encoded as

adrs 4 3 2 1

kD kD kD k=+++ (5)

where

k,,k " are integers between 0 and D1

−

and represent the cell indices for

,y,

. At each

address representing a cell, there is a solution

number, followed by the values of model parameters

(

) for the particular cell and solution.

During the online phase, given the desired sub-

posture (e.g.

dddd

v,z,y,x ), the cell indices

134

k,,k,k " are computed as follows. Suppose the

range of a posture variable, say v, is

min

v to

max

v ,

and the cell size length is

v , then the index

k is

computed as

dmin

k ceil

⎛⎞

−

⎜⎟

⎝⎠

(6)

where ceil denotes the ceiling of the quantity. Other

cell indices

432

k,k,kfor

,y,zare computed

similarly and the address in the file is determined via

(5).

Since the data is stored in the file with

increasing order of the address, a binary search is

conducted to locate and access the cell data. The

binary search performs

)N(log

cell2

comparisons in

the worst case. Once the parameters for each

solution are retrieved, the joint angle values are

computed via (4).

The wrist joint angles

765

,, are modeled

similarly to achieve the desired orientation.

However, these joints angle are dependent both on

the first four joints and the desired orientation. In

addition the wrist joint angles have a more complex

relationship with the orientation. As a result we

express the wrist angles as a linear relation with the

first four joint angles and a quadratic relation with

the orientation angles of the form

ii1234 i

T222

iii

b( ) c( )

d( ) e( )

i5,6,7

θθθθθ αβγ

βαγ βγ α β γ σ

(7)

where

b is a 41

parameter vector,

c ,

d and

are

parameter vectors and

σ is a scalar

parameter. These parameters are obtained using a

least squares method, and are stored as records

similar to the procedure given above for the first

four joint angles. The cells for the orientation will

be 7-dimensional, and (5) will be a 6-th order

polynomial. The on-line procedure is also identical

to those of first four joint angles. Since no

trigonometric or inverse trigonometric functions are

involved, the computation is extremely fast.

4.2 Neural Network Model

It is well known that backpropagation neural

networks can be used for approximation. In this

section we describe a simple neural network model

to approximate the inverse kinematics relationship.

For the position kinematics, the neural network

consists of an input layer with a

4N× weight

matrix

W , where 4 is the number of inputs

INFORMATION-BASED INVERSE KINEMATCS MODELING FOR ANIMATION AND ROBOTICS

,y,

, N is number of neurons in the hidden

layer, and the output layer has 4 outputs representing

4321

,,,

. The inputs v,

,y,

are first

normalized as

min

max min

2( x x )

(x x )

−

=−

−



(8)

where

min

and

max

are, respectively the minimum

and maximum values of the x data in the cell.

Similarly

y,z,v are normalized so that their ranges

are between –1 and +1. The output of the input

layer p is thus

in in

ˆˆ ˆ

p(xyzv)W b=+

(9)

where

b is a constant 1N× bias vector. A

tangent sigmoid function of the following form is

applied to p to obtain

q 1; j 1,2,...N

−

=−=

(10)

Finally, the normalized joint angle vector is obtained

from

1234 outout

ˆˆˆˆ

()qWb

θθθθ

=+ (11)

where q is an

1N× vector

out

W is an N4× matrix

and

out

b is a 14× output bias. The actual

(denormalized) joint angles are obtained from

i i,max i,min i i,min

()(1)

θθθθ θ

=− ++ (12)

where

i,max i,min

are the minimum and maximum

values of

in the cell. The neural network is then

trained with the cell data points to obtain weight

matrices and bias vectors.

The data to be stored for the on-line phase are the

weight matrices

W and

out

W , bias vectors

b and

out

b and minimum and maximum of

,y,

12 34

,,,

θθθ

for each cell. During the on-

line phase, given the desired values of

,y,

these values are normalized via (8), passed through

the input, hidden and output layers by applying (9)-

(11). The actual (denormalized) joints values are

finally found from (12).

Orientation kinematics is obtained similarly to

the above, except that the inputs to the network

are

12 34

,,,

θθθ

obtained above and the orientation

angles

,, . The outputs of the network are the

joint angles

567

θθ

. The input and output

weight matrices

W and

out

W are now 7N× and

, and the bias vectors

b and

out

b are

and 13

, respectively.

5 PERFORMANCE ANALYSIS

In this section we apply the proposed method to the

Puma 560 manipulator and the anthropomorphic

arm. The reason for the choice of the Puma 560 is

that it is a well known and extensively researched

manipulator, and serves as a bench mark.

Furthermore, it has a closed form inverse kinematics

and thus the correctness and success rate of the

proposed method can be checked against the known

results of the Puma 560.

5.1 IK Modeling of Puma 560

The joint angles ranges of the Puma are given in

Table 1. The first three joints, or the major joints, of

the Puma 560 are waist, shoulder and elbow joints,

and determine the position of the end-effector.

Therefore, we can express the first three joints in

terms of

x, y and z only. The fully stretched arm is

about

900 mm long, and we assign ranges for each of

x, y and z directions from –900 mm to +900 mm,

with the cell side length of 200 mm which forms

cubes of volume

100 100 100 mm×× . There are a

maximum of

(

)

1800

100

5832= cubes (cells), but only

about 3400 of them contained generated postures

due to the joint angle limits. The maximum number

of cells for the orientation kinematics with cells

sizes of 20 degrees for

12 3

θθ

, and 45 degrees for

,, for the ranges of these angles are

17 14 17 8 8 8 2,071,552

××××= .

We used the polynomial model (4) and (7).

The number of joints for position is three and only x,

y and z are present, thus

a , i=1,2,3 in (4) are

vectors.

Table 1: Joint angle ranges (limits) for Puma 560

–170

+170

–225

+45

–250

+75

–135

+135

–100

+100

–180

+180

ICINCO 2005 - ROBOTICS AND AUTOMATION

The Puma 560 has a maximum of four

solutions, i.e. elbow up/down, left/right arm, for

positioning of the end-effector, and eight solutions

for position and orientation, which were found using

the classification. The parameters of the above

models were found for each of the four solutions in

each of the cells using a least squares method.

These parameters were stored in a file for each cell,

and the total storage needed was about 372 KB for

position kinematics and 340 MB for the orientation

kinematics. Note that memory and disks are very

cheap (e.g. about $100 per 1 GB of memory and

about $60 for a 100 GB disk), and are readily

available on a PC.

In order to test the validity of the models, we

generated randomly 1000 position and orientation

postures within the ranges of

x, y, z and

,, .

The polynomial model (4) and (7) were used to

obtain the joint angles. The results are summarized

in Table 2a and Table 2b.

Table 2a: Position kinematics – Polynomial model

A B C D E

1 908 99.3 2.92 2.37

2 500 98.6 2.80 2.17

3 518 98.6 2.83 2.36

4 927 99.2 2.92 2.41

A: Number of solutions

B: Number of valid configurations

C: Success rate (%)

D: Mean absolute position error (mm)

E: Error standard deviation (mm)

Table 2b: Orientation kinematics – Polynomial model

A B C D E

1 340 97.3 2.10 2.92

2 144 97.3 1.96 2.45

3 276 96.2 1.83 2.15

4 372 97.4 1.96 2.34

5 385 98.2 2.22 2.73

6 238 96.0 1.94 2.62

196 97.1 1.95 2.88

8 369 95.7 1.81 2.38

A, B , C: as defined in Table 2a.

D: Mean absolute orientation error (degrees)

E: Error standard deviation (degrees)

The success rate is defined as the ratio of the

number of valid configurations found by the method

to those found by the closed-form inverse kinematic

equation. It is seen that the success rates are high

ranging from

89% to 100%. The error is defined as

the difference between the desired and actual end-

effector position, and orientation. The actual values

are determined by substituting the joint angles found

by the method in the forward kinematics equations.

It is seen from Table 2 that the mean absolute

position and orientation errors are about 1.8 mm,

and 4.5 degrees, respectively.

Now consider the neural network model (8)-

(12) applied to the Puma 560, however the cell size

for position was increased to 200 mm providing

only 646 cells for position. The size of orientation

cells is the same as in the case of polynomial model.

Several experiments were conducted to determine

the number of neurons for accuracy, simplicity and

success rate and it was found that

N = 5 provided a compromise among these

characteristics. The maximum amount of memory

needed for storing weight matrices, bias vectors and

minimum and maximum values for normalization

and denormalization were 573 KB for position and

605 MB for orientation which are between 1.5 to 1.7

times of those of the polynomial model.

The results are now summarized in Tables 3a

and 3b. It is seen that the success rates are very high

ranging from 92% to 100%, which are higher than

the polynomial model. The position errors are about

2.5 mm and the orientation errors are 2.9 degrees

which are somewhat better than the polynomial

model given in Table 2. The online time, however,

is two to three times more than the polynomial

model. This is due to the higher number of

parameters and operations needed in the neural

network model.

Table 3a: Position kinematics – neural network model

A B C D E

1 880 91.6 1.74 1.31

2 465 89.1 1.91 1.32

3 451 91.1 1.92 1.42

4 830 94.0 1.77 1.36

A,B,C,D,E : See definitions in Table 2a

Table 3b: Orientation kinematics - neural network model

A B C D E

1 350 97.3 1.75 2.68

2 160 97.3 2.67 2.54

3 260 96.2 3.09 5.62

4 813 97.4 2.33 3.71

5 392 98.2 3.62 6.35

6 205 96.0 2.27 2.94

7 196 97.1 4.41 7.11

8 368 95.7 1.48 1.89

A,B,C,D,E: See definitions in Table 2b.

The total on-line time T to compute different

configurations for a desired posture consists of

several components as follows:

T : Checking to verify that the desired point

ddd

z,y,x is reachable.

T : Computing the cell indices and the addresses

in the file for position and orientation.

T : Applying a binary search to locate the address

in the file where model parameters for various

INFORMATION-BASED INVERSE KINEMATCS MODELING FOR ANIMATION AND ROBOTICS

solutions are stored, and retrieving these

parameters.

T : Computing joint angles using (4) and (7) for

polynomial model, and (8)-(12) for the neural

network model.

The total computation time is the sum of the above

four time components. The online computation was

done on a Pentium 4, 3.0

GHz computer with a C

program. Table 4 show the total online time for

each model. Note that the time is in microseconds

for computing all solutions (a maximum of eight)

averaged for 1000 randomly generated postures.

For the sake of comparison, the solutions were also

computed using the closed-form inverse kinematics

of the Puma 560. These closed form equations were

programmed in C with an optimized implementation

to perform the least amount of computation. The

total time using the closed-form inverse kinematics

computation was 24 microseconds, which is 10

times slower than the proposed method with the

polynomial model, and 4 times slower than the

neural network model. The contrast is much greater

for robots that do not have closed-form solutions.

Our analysis and simulations have shown that the

proposed method can be two to three orders of

magnitude faster than other techniques for

manipulators without closed forms kinematics.

Table 4: Total computation times in microsecond

Polynomial

Position

Polynomial

Orientation

Neural Net

Position

Neural Net

Orientation

0.54

1.58

2.16

4.66

5.2 Modeling of Anthropomorphic

Arm

The procedures described above were applied to the

anthropomorphic arm described before. The ranges

of the spherical shoulder joints (

321

,, ), elbow

(

) and the spherical wrist joints (

765

,, ) are

given in Table 5. The upper arm length is 334 mm

and lower arm length is 288 mm. The length and

joint limit data were obtained from a study

conducted by NASA.

Table 5: Joints ranges for the anthropomorphic arm

–39

164

–61

187

–83

210

149

–40

–59

–78

The fully stretched arm is about 600 mm long,

and we assign ranges for each of

x, y and z from –

600 mm

to +600 mm, with the cell side length of 60

. The range of inclination angle is –100 degrees

to +40 degrees with the cell size of 10 degrees.

With these ranges, the maximum number of cells is

129,654.

The polynomial model (4) for the position

requires a maximum storage of 14.9 MB if all cells

contain data and each cell has the maximum of four

solutions. An experiment involving 1000 randomly

chosen values of (

,y,

) was carried out and the

values of (

4321

,,, ) were found using the

acquired IK model parameters. These values were

then substituted in the forward kinematics to

determine the accuracy of the solution. Table 6a

shows the number of cells containing 1, 2, 3 or 4

solutions, and the average and standard deviation

position errors for each solution. These errors are

quite acceptable for animation applications.

Furthermore since there is no closed form solution,

the success rate cannot be estimated for the arm, but

is believed to be similar to that of the Puma 560.

Note also that the smaller number of valid solutions

compared to the Puma 560 is due to the limited

ranges of the anthropomorphic arm joint angles and

specification of (restriction on) the elbow

inclination.

Table 6a: Position kinematics – Polynomial model

A B C D

1 481 1.97 1.32

2 89 2.91 2.16

3 61 2.45 2.09

4 41 2.86 2.07

A: Number of solutions

B: Number of valid configurations

C: Mean absolute position error (mm)

D: Error standard deviation (mm)

Table 6b: Orientation kinematics – Polynomial Model

A B C D

1 52 2.41 2.07

2 12 3.66 2.90

3 10 3.63 1.37

4 3 2.00 1.38

5 38 2.89 2.35

6 9 3.07 2.99

7 8 3.52 2.34

8 6 3.11 1.13

A, B: See Table 6a for definitions.

C: Mean absolute orientation error (degrees)

D: Error standard deviation (degrees)

To obtain the wrist angles

765

,, , the

ranges of

,,,,,,

4321

were divided into

cells of side length 20 degrees for the joint angles,

and 45 degrees for the orientation angles. The

maximum number of cells is 8,785,920, but not all

these cells contain data. The parameters of the IK

model were obtained using (7) as described before.

The actual storage for the data is about 1 GB. Note

ICINCO 2005 - ROBOTICS AND AUTOMATION

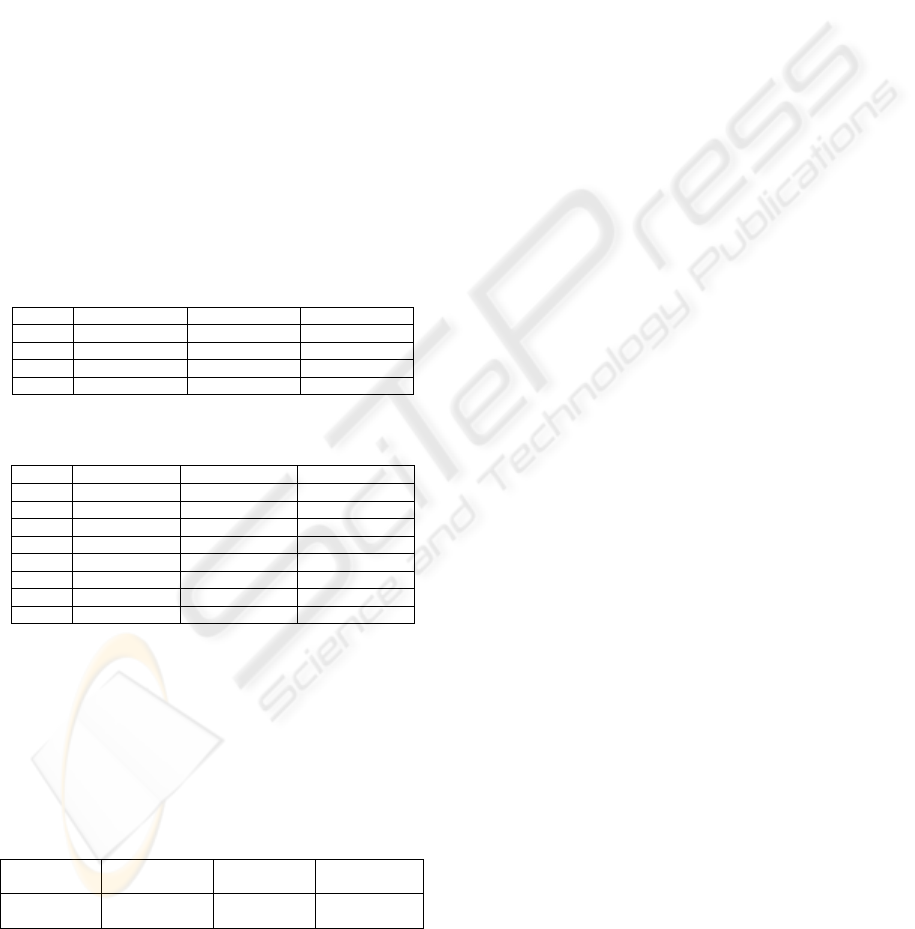
that even though this arm is 7-DOF, the storage

requirement is not much higher than that of the 6-

DOF Puma due to the fact that the ranges of the joint

angles the arm are lower than Puma 560. An

analysis similar to the above was carried out

involving randomly selected postures, and the

results are shown in Table 6b. The average and

standard deviation errors in orientation are about 3

degrees, which are quite acceptable for the

animation applications. Since closed form

kinematics is not known for this arm, the success

rate cannot be found, but the results of the

experiments reported in Section 5.1 indicate that

success rate of the proposed method is high.

We now report the results for the neural

network model using (8)-(12), which are

summarized in Table 7a and 7b. Comparison of

tables 6 and 7 indicates that better position and

orientation accuracy are obtained using the neural

network.. However, the disadvantage of the neural

network model is the need for much higher off-line

time for training.

Table 7a: Position kinematics – neural network model

A B C D

1 495 0.87 1.32

2 103 1.66 2.16

3 66 1.47 2.09

4 47 1.48 2.07

A,B,C,D: See the definitions in Table 7a.

Table 7b: Orientation kinematics – Polynomial Model

A B C D

1 43 1.14 0.66

2 10 1.50 1.82

3 9 1.68 1.55

4 1 0.44 0.0

5 39 1.60 1.82

6 9 2.46 3.07

7 7 2.53 2.04

8 5 3.81 2.82

A,B,C,D: see the definitions in Table 6b.

The online computation times for the two

models are given in Table 8. These times measured

in microsecond are for computing all solutions (i.e. a

maximum of 8) averaged over all the randomly

chosen postures. The online computation time is

extremely low which enables real-time computation

for animation applications involving many limbs.

Table 8: Total computation times in microsecond

Polynomial

Position

Polynomial

Orientation

Neural Net

Position

Neural Net

Orientation

0.1

0.3

0.7

0.9

6 CONCLUSIONS

A novel method for the inverse kinematics solutions

of anthropomorphic limbs and fast manipulators has

been proposed. The method uses the information

that is processed and stored during off-line for rapid

on-line access and evaluations. It decomposes the

workspace into cells, and uses a classification

technique to isolate various solutions. Both

polynomial and neural networks have been

investigated for modeling the inverse kinematics

solutions in a cell. It has been shown that both

models provide good position and orientation

accuracy and high success rates, with the neural

network having somewhat better performances in

these regards. However, the neural network requires

more off-line time to determine the parameters of

the model due to training, and also the on-line time

is slightly higher due to the need for more complex

operations.

The method is especially appealing for use in

animation and graphics applications. In these

applications, high position and orientation accuracy

is not required, and thus an approximation of the

inverse kinematics is sufficient. In addition, the

animation characters require satisfying many

constraints, in addition to joint limits, to make the

motion natural and human like. These constraints

can easy be checked and incorporated within the

proposed method during the off-line configuration

generation. It is also noted that animation

applications involve a number of characters each

with several 7-DOF limbs. In such applications,

very high speed of computation is required, e.g.

often several thousand inverse kinematics

computation per second for a 7-DOF limb is

desirable, which the proposed method can readily

achieve. By providing all solutions for a given

posture, the method allows the animator to select the

solution that is most visually attractive for showing

a particular motion.

REFERENCES

Chapelle, F., and P. Bidaud, 2001. A Closed form for

inverse kinematics approximation of general 6R

manipulators using genetic programming”

Proc. IEEE

Int. Conf. Robotics and Automation

, pp. 3364-3369.

Chiacchio, P., S. Chiaverini, L. Sciavicco and B. Sciliano,

1991.Closed-loop inverse kiematic schemes for

constrained redundant manipulators with task space

augmentation and task priority strategy,”

Int. J.

Robotics Research

, pp. 410-425, vol. 10, no. 4.

Chiaverini,S., B. Sciliano and O. Egeland, 1994. Review

INFORMATION-BASED INVERSE KINEMATCS MODELING FOR ANIMATION AND ROBOTICS

of dampedleast squares inverse kinematics with

experiments on an industrial robot manipulator,”

IEEE

Trans. Control Systems Technology

, pp. 123-134, vol.

2, no. 2, 1994.

De Lope, R. Gonzalez-Careaga, and T. Zarraonandia,

2003. Inverse kinematics of humanoid robots using

artificial neural networks,” EUROCAST 2003,

Proc.

Int. Workshop on Computer Aided System Theory

p.216-218.

Dermatas E., Nearchou A., and Aspragathos N

.,1996.

Error - Backpropagation Solution to the Inverse Kinematic

Problem of Redundant Manipulators," Journal of

Robotics and Computer Integrated Manufacturing

, pp.

303-310, vol. 12, no. 4.

Khwaja,A., M. O. Rahman and M.G. Wagner, 1998.

Inverse Kinematics of Arbitrary Robotic Manipulators

Using Genetic Algorithms, in J. Lenarcic and M. L.

Justy (editors),

Advances in Robot Kinematics:

Analysis and Contro

l, pp. 375--382, Kluwer Academic

Publishers.

Klein, C.A. and C. H. Huang, 1983. Review of pseudo-

inverse control for use with kinematically redundant

manipulators,”

IEEE Trans. Systems, Man, and

Cybernetics

, vol. SMC-13, no. 3, pp. 245-250.

Lloyed, J.E., and V. Hayward, 2001. Singularity robust

trajectory generation,” Int. J. Robotics Research, pp. 38-

56, vol. 20, no. 1.

Manchoa, C. and J.F. Canny, 1994. Efficient inverse

Kinematics of general 6R maipulators

,” IEEE Trans.

Robotics and Automation,

pp. 648-657, vol 10, no. 5.

Nearchou, A.C., 1998. Solving the inverse kinematics

problem of redundant robots operationg in complex

environments via a modified genetic algorithm”,

Mech. Mach. Theory

, vol. 33, no. 3, pp. 273-292.

Press,W.H., B.P. Flanny, S.A. Teukolsky, and W.T.

Vetterling, 1988.

Numerical Recipe in C, Cambridge

University Press, Cambridge, U.K.

Seraji, H., M.K. Long and T.S. Lee, 1993. Motion control

of 7- DOF arms: the configuration control approach,”

IEEE Trans. Robotics and Automation, pp. 125-139,

vo. 9, no. 2.

Tarokh, M. and K. Keerthi, 2005. Inverse Kinematics

solutions of Anthropomorphic Limbs by Decomposition

and Fuzzy Classification, in

Proc. Int. Conf. on

Artificial Intelligence

, Las Vagas.

Tolani, D, A. Goswami and N. Badler, 2000. Real-time

inverse kinematics techniques for anthropomorphic

limbs,”

Graphic Models, pp. 353-388, vol. 62.

Uicker, J. J, J. Denavit and R.S. Hartenberg, 1984. An

iterative method for the displacement analysis of

spatial mechanisms,

J. Applied Mechanics, ASME, pp.

309-314.

Whitney, D.E., 1972. The mathematics of coordinated

control prosthetic arm and manipulators,”

Trans. ASME J.

Dynamic Systems, Measurement and Control

, pp.

303-309, vol. 94.

Zhao, X. and N. Badler, 1994. Inverse kinematic

positioning using nonlinear programming for highly

articulated figures,”

Trans. Computer Graphics, pp.

313-336, vol. 13, no. 4.

ICINCO 2005 - ROBOTICS AND AUTOMATION