DECOMPOSITIONS OF HIERARCHICAL STATE ESTIMATION
STRUCTURES
Problems and Strategies
Rogério Bastos Quirino
Department of Electromechanical Technology, CEFET/MD-PR, 85884-000, Medianeira, PR, Brazil
Celso Pascoli Bottura
Department of Machines, Components, and Intelligent Systems, FEEC/UNICAMP, 13083-970, Campinas, SP, Brazil
Keywords: Kalman filters, Hierarchical Structures, Estimation Theory, Distributed Models, Hierarchical Control.
Abstract: This study has three main objectives. First, to p
oint and discuss the principal features, advantages, and
limitations of distributed state estimators. Second, to analyze structures and methodologies related to the
distributed state estimation problem, with emphasis on the heterarchical one. Finally, to delineate some
prospects for future investigations.
1 INTRODUCTION
To provide a complete description of a complex
system and its effective control requires a great
quantity and variety of sensors. Multiple sensors
provide more information and hence a better and
more precise understanding of a system and its
operation. Multisensor systems have found
applications in process control, robotics, navigation,
aerospace, meteorology, manufacturing, energy
generation and defense systems, among others.
A multisensor system may employ a range of
di
fferent sensors, with different characteristics, to
obtain information about a real system. The diverse
and sometimes conflicting information obtained
from multiple sensors give rise to the problem of
how the information may be combined in a
consistent and coherent description of the
environment under observation. This is one of the
problems of data fusion in multisensor networks that
hence requires the elaboration of methods that
establish how the information derived from a
multitude of sensors can be combined, in order to
obtain plausible descriptions of the observed system.
Many data fusion problems in multisensor
net
works involve a distributed state estimation
process. The fusion of information, for example, on
the multi-target tracking problem, involves two
important phases: distributed state estimation –
treated in this article – and data association.
Within this context, considerable attention has
been
given to the development of distributed and
parallel versions of the Kalman filtering algorithm
(Kalman,1961), known as the best unbiased linear
estimator or the optimal linear estimator under
Gaussian assumptions and that serves as basis for
our investigation.
The motivation for the material presented in this
art
icle derives from two important aspects:
1) From the benefits and importance of the
m
ultisensor systems, particularly, the distributed
systems of data fusion.
2) From the existence of a narrow gap in the
literatu
re to a modest, but constructive synthesis
of distributed state estimation methods.
Two main categories of distributed state
estim
ation architectures: hierarchical and
heterarchical (Talukdar et al.,1992) are presented
and appraised. This serves the purpose of explaining
the advantages of heterarchical distribution. A
working definition for a heterarchical system is then
established and the benefits of such a system
outlined. The aim is to show that, although
sometimes suboptimal, this kind of distributed state
124
Bastos Quirino R. and Pascoli Bottura C. (2005).
DECOMPOSITIONS OF HIERARCHICAL STATE ESTIMATION STRUCTURES - Problems and Strategies.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 124-131
DOI: 10.5220/0001165001240131
Copyright
c
 SciTePress

estimation structure is feasible and can lead to
additional advantages, for example, for the case of
considering the information space instead of the
state space as a starting point for distributed
structure generation (Mutambara,1995).
The problems associated with a fully connected
topology, and alternative strategies for heterarchical
distributed estimation are outlined.
An heterarchical distributed state estimation
structure, is defined as a data processing system in
which all information is processed locally and there
is no centralized or coordinator processing site, in
opposition to an hierarchical distributed state
estimation. It consists of a network of sensor nodes,
each with its own processing facility, which do not
require any centralizer or coordinator module. In
other words, there is no explicit hierarchy. It is
important to highlight that the existence of
information exchange among the levels - under
centralization - and among the subsystems at the
same level – under coordination - in the hierarchical
structures depend on mathematical development
employed in the hierarchization of the Kalman filter
discussed in section 2.
2 FORMULATION OF THE
HETERARCHICAL
DISTRIBUTED STATE
ESTIMATION PROBLEM
The general theory of hierarchical systems was and
is continuing to be applied to control and estimation.
This application involves optimization techniques –
minimum variance in the Kalman approach – and
concepts of hierarchical structures.
The aim is to construct state estimation
architectures with different performance degrees.
In this section, we briefly treat the principles of the
hierarchical state estimation theory, presented in
(Chong,1979), due to its importance to the
comprehension and development of distributed state
estimation topologies.
In the sequence, we present and analyze the
dynamics of the hierarchical structures to yield
distributed state estimation methods.
2.1 Fundamentals
We intend to illustrate the estimation problem of a
stochastic state vector
x
conditioned to the
innovations from two observations
and .
Given the local estimates of
1
y
2
y
x
, ,
and the error covariances matrices
associated, we wish to find the global estimate
and the corresponding error
covariance matrix.
)/(
ˆ
11
yxEx =
)/(
ˆ
22
yxEx =
),/(
ˆ
21
yyxEx =
The main issue that this well-known formulation
leads to the heterarchical distributed state estimation
problem is the following: which dynamics of
information exchanging in the decomposed structure
preferably would satisfy the minimum variance
criteria for the global estimate
?
x
ˆ
The necessary and sufficient conditions for the
global estimation can be interpreted as follows. If
(
)
21
~
,
~
yy
, innovation’s subspace, and
(
)
21
ˆ
,
ˆ
xx
,
distributed estimation subspace, are related by
invertible transformations, then
(
)
21
~
,
~
yy
and
(
)
21
ˆ
,
ˆ
xx generate the same subspace. In general,
(
)
21
~
,
~
yy
and do not generate the same
subspace. This prevents the optimal fusion in the
Kalman sense. Therefore, the optimal fusion is
possible when the projection of
)
ˆ
,
ˆ
(
21
xx
x
on
(
)
21
~
,
~
yy
lies
in the same subspace generated by
. )
ˆ
,
ˆ
(
21
xx
In the case which
does not lie in the
same subspace generated by
and , as shown
in Fig. 1, we can adopt the following approaches:
)(
ˆ
optimalx
1
ˆ
x
2
ˆ
x
a) To construct a heterarchical distributed state
estimation structure based on the exchange of local
state estimates and data
β
resulting from a
transformation
that establishes an approximate
relationship between the local subsystems and the
global system.
allows us to yield
an heterarchical estimation structure in which
the data
β
i
Τ
β
i
Τ
β
are transmitted between the
subsystems at an unique level. This estimation
structure would be suboptimal in the Kalman
sense;
b) Alternatively, to construct an estimation
structure to enlarge the subspace generated by
,
2
and
1
ˆ
x
ˆ
x
β
, through the incorporation of an
DECOMPOSITIONS OF HIERARCHICAL STATE ESTIMATION STRUCTURES - Problems and Strategies
125

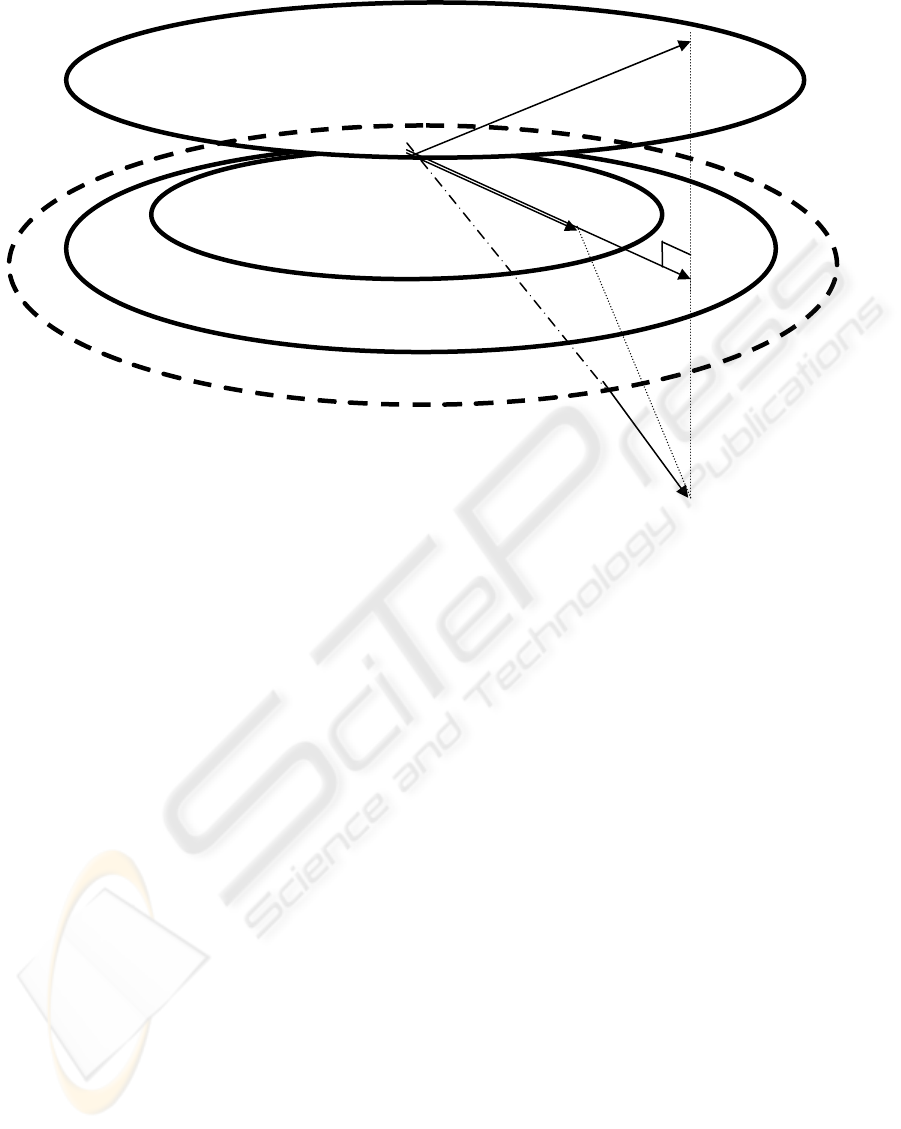
Figure 1: Geometric view of the heterarchical distributed state estimation (Ω- totally decoupling subspace: td ; Φ- partially
decoupling subspace: pd ; ψ- coupling subspace)
information set
η
>
β
, where
β
η
⊃
, until
lies in this enlarged subspace. The data
resulting from the transformation
establishes an exact relationship between the local
and global models.
)(
ˆ
optimal
x
)
~
,
~
(
21
yy η
η
i
Τ
These data are transmitted between the levels of
such a hierarchical estimation structure that is
coordinated or centralized.
If we wish to minimize the communication in the
second approach, without compromising the
performance of the estimation structure, the
dimension of the data vector
η
must be reduced as
much as possible obeying the restriction
η
>
β
.
Once the estimation is generated, the
innovation’s subspace
(
)
21
~
,
~
yy
becomes equivalent
to
, denoted as the optimal distributed
state estimation subspace.
),
ˆ
,
ˆ
(
21
η xx
If an inherently global system is totally
decoupled, the subspaces
,, Ψ
Ω
and constitute
an unique subspace within the innovation subspace
. In this case, the estimation structure
would be inherently heterarchical.
Φ
)
~
,
~
(
21
yy
3 STRATEGIES OF
HETERARCHICAL
DISTRIBUTED STATE
ESTIMATION
The strategies of decomposition in order to obtain
heterarchical distributed state estimation structures
can be developed for the prediction stage as well as
for the correction stage of the Kalman filter, for
instance. The decomposition only of one or both
stages will depend on the existence of correlation
between the observation and state noises of the
system’s model. In (Hashemipour & Laub,1987), for
example, the strategies of decomposition are
developed for both stages.
The problem of heterarchical distributed state
estimation formulated in this work deals exactly
with the decomposition of the correction stage and is
based on the original version of the Kalman filter
(Kalman,1961) as well as on its alternative Inverse
Covariance form (Anderson & Moore,1979).
)
ˆ
,
ˆ
(
2
1
x
x
Ω
)(
ˆ
suboptimal
td
X
x
)
2
,
1
(
~
~
yy
)(
ˆ
suboptimal
pd
x
),
2
,
1
(
ˆˆ
β
x
x
Φ
),
2
,
1
(
ˆˆ
η
x
x
Ψ
)(
ˆ
optimal
x
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
126

3.1 Strategies via Matrix
Partitioning
These strategies are based on the Inverse Covariance
of the Kalman filter (Anderson & Moore,1979).
Consider the global system model:
kkkk
wxAx
+
=
+1
(1)
where w
k
is independent of x
0
assumed Gaussian
with covariance P
0
.
In addition, consider a set of N local observations
concerning the global system (1), comprised by the
following equations:
(2)
Ni
i
kk
i
k
i
k
vxHy ,...,2,1, =+=
where the v
i
, measurement noises, with covariance
R
i
k,
are independent among themselves and
independent of w
k
and x
0
.
For the heterarchical distributed state estimation
problem we assume that the local processing
algorithms are solved based on local models
described by:
(3)
i
k
i
k
i
k
i
k
wxAx +=
(4)
i
k
i
k
i
k
i
k
vxCz +=
where i=1,2,..,N.
Consider the global system with the state x,
decomposed into two subsystems with states x
1
and
x
2
. The local observations, y
1
and y
2
, in (1)-(2),
based on the knowledge of x, provide an exact
representation of the process. On the other hand, the
models describing the local subsystems states, x
1
and x
2
, of the global system x, and the local
observations based on knowledge of x
1
and x
2
, in
(3)-(4), could provide only an approximate
representation of the global system state x.
Alternatively, x
i
might exactly represent x. In this
case x
i
is a Markovian process identical to x. On the
other hand, it may be true that x
i
≠ x. In this case,
could exists a nodal transformation matrix T
i
such
that x
i
=T
i
x. If T
i
does not exist, then or x
i
represents
a subvector not considered in the global model x, or
x
i
represents an approximate model of this global
model. This approximation can be reached using
reduced order models, derived from relaxation of
part of the correlations of the global model.
The global state estimation that will be processed
in a centralized node, based on the observation of
the global system (2), can be written as follows:
∑∑
+−=
==
−−
N
i
i
N
i
i
t
iii
t
i
yRHPxHRHPxx
11
11
ˆ
(5)
where
≡
x
prediction of x.
≡
P
covariance of the estimation error of x.
If there is a transformation T
i
that satisfies the
relationship between the local and global dynamics
such that the measurements
y
i
and z
i
in (2) and (4)
become exactly or approximately compatible, then
processing at the local nodes solves the following
local estimation problem:
]).
.(
ˆ
[
1
111
iiii
iii
t
iii
t
i
xHR
HIxPyRH
Γ
−−Γ=
−
−−−
(6)
where
i
Γ
is the nodal transformation matrix that
satisfies
i
Γ
= . and # denotes the pseudo-
inverse.
#
i
C
i
H
From (5) and (6) we have:
∑
Λ−+Λ=
=
N
i
iiii
xxGxx
1
)
ˆ
(
ˆ
(7)
where
(8)
;
;
;
1
1
1
1
iii
t
iii
i
t
ii
N
i
ii
t
i
HRHPI
PPG
HRHPI
Γ−=Λ
Τ=
−=Λ
−
−
=
−
∑
It is important to point out that if at least an
unique nodal transformation matrix
provides
only just an approximate representation for the i-th
sub-state, then the global state estimation based on
the gobal reconstructibility will not be optimal in the
Kalman sense.
i
Γ
In general, the local estimates
are not
independent. The correlation between these
estimates is taken account through the P matrix. The
local correction gain
given in (8) incorporates
the influence of these correlations in the global
estimation process represented in (7).
i
x
ˆ
i
G
DECOMPOSITIONS OF HIERARCHICAL STATE ESTIMATION STRUCTURES - Problems and Strategies
127

If there is a nodal transformation
in (8) that
transforms the global model in a feasible local
model, such that P, for example, be diagonalizable,
then we can construct an heterarchical and
suboptimal global estimator based on a set of
communicated data of dimension less than
,
i=1,2,...,N, by undoing the hierarchy.
i
Τ
)
ˆ
(
i
x η
In principle, the strategies via matrix partitioning
(Chong,1979) and (Hashemipour & Laub,1988), as
well as the strategies via the multiple projections
(Hassan et al.,1978), presented in the following
subsection, require centralizer and coordinator
modules, respectively, in order to fuse the local
estimates in such hierarchical estimation structure.
3.2 Strategies via Sucessive
Orthogonalizations
These strategies are based on the original version of
the Kalman filter (Kalman,1961). In this class of
strategies each local node disposes only of its local
model that represents exactly a subsystem of the
global system. Therefore, the construction of
heterarchical distributed structures based on these
strategies assumes the existence of a nodal
transformation
, not explicit, however obvious,
that satisfies exact relationships between the global
system and the local subsystems.
i
Τ
From this assumption results the requirement of a
coordinator module in order to give support to the
local estimates processing.
Consider the following representations for the
local models:
(9)
i
k
i
k
i
k
i
k
i
k
j
k
N
ij
i
ij
k
i
k
i
k
i
k
vxHy
wxAxAx
+=
++=
∑
≠
=
+
1
1
where the same assumptions made to the noise
variables in (1) and (2) are held.
The key idea of the multiple projections method
consists in the decomposition of the correction stage
of the Kalman filter through the orthogonal
projection of the state
on the observation vector
of the global system. The observation vector is
partitioned into N components of local observations.
i
x
In this way, the following estimation result is
obtained:
∑
+=
=
−
N
i
i
i
iii
yxExx
1
1
)
~
/(
ˆ
(10)
where
generates the Hilbert subspace:
∑
=
−
N
i
i
i
y
1
1
~
;
~
...
~
~
~
1
)/(
2
)/(3
)/(
1
2
)1/(
1
−
−
⊕
⊕⊕⊕
N
kkN
kk
kk
kk
y
yyy
(11)
)/(
1−
Υ=
k
ii
xEx ;
≡
Υ
−1k
observation subspace until the (k-1) instant.
The corrections based on the (N-1) nonlocal
innovations, described by (10), constitute the
coordinated hierarchical nature of the Kalman filter.
In this hierarchical structure the important task of
incorporating the inherent correlations among the
local models, a priori partitioned exactly, and the
global model, is made by the coordinator. In this
way, the optimality of the estimation with
coordinated hierarchy, in the Kalman sense, is
preserved.
In (Quirino & Bottura, 2001) a nodal
transformation
on the local state is proposed,
that is not explicitly a priori transformed by
in
(Hassan et al.,1978), in order to obviate the
incorporation of the (N-1) nonlocal innovations
described in (11). Such incorporation that in the
original structure is proposed in (Hassan et al.,1978),
it must be considered by each one of the local
estimators.
β
i
Τ
η
i
Τ
4 DISCUSSIONS
The approach taken in this study for distributed state
estimation is motivated by important contributions
that exist in the literature. These works take the
Kalman filter as the starting point to derive the
parallel structures for state estimation. However, a
gap resides in the fact that the great majority of the
proposed structures are concentrated around
hierarchical structures and do not sufficiently go
beyond them in the sense we explore here.
We believe that in this work we fill part of that
gap through the explicit discussion of techniques and
strategies of how to undo the hierarchical structures
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
128

in order to generate the heterarchical distributed
structures, as here discussed.
The parallelizations of the Kalman filter equations
are achieved for one or more of the different stages:
1) parallelism at the prediction stage; 2) parallelism
at the correction stage; and 3) parallelism via
segmentation.
Another interesting technique to parallelize the
Kalman filter was developed in (Travassos,1980), in
which the prediction and correction equations are
simultaneously processed. The forced decoupling
between these stages is maintained for the interval of
one iteration during the whole history of the filter.
However, the filter proposed is suboptimal, in the
Kalman sense, as proved in (Hashemipour &
Laub,1988), through the analysis of the estimation
error covariance matrix. This technique will not be
considered in this work, and remains open for future
investigation.
The principal drawback of the hierarchical
structures, usually resides in the fact the coordinator
or centralizer module, though undone, still requires
great computational and communication efforts for
its implementation in a distributed environment.
Hierarchical structures present a low performance
from the point of view of communication and
synchronization requirements, mainly when the
number of partitioned subsystems increases. The
bottleneck in processing for hierarchical structures is
caused by the centralizer or by the coordinator
fusion of the information originating in the lower
levels.
As recently commented, though these fusion
modules coordinator as well as centralizer can be
decomposed, e.g., by strictly computational
procedures, generally, they still can generate fully
connected structures with equal or great
communication and computational requirements
than the ones of the original structures. In addition to
this, the gain achieved with respect to the
communication and synchronization requirements
through e.g., merely computational procedures, is
not significant, as shown in (Quirino et al.,1988).
In order to minimize the effects of these
restrictions we must reflect about the following
question: How the proposal of partitioning the
subsystems can improve the consistency of the
distributed local estimates? It is because, depending
on the used partitioning proposal the distributed
local estimates could result from almost purely or
purely local data implying in different performances
of these distributed local estimators.
Within this context, there are controversies on the
above mentioned questions: e.g., why the inherently
hierarchical structures, yet do not present a good
performance, if: a) The global estimate derived from
local estimates can locally preprocess more data
without any loss of global performance?; b) Local
filtering may reduce the required bandwidth for
transmission of information to a centralizer or
coordinator processor?; c) For local models with
dimension smaller than for the global models
potential advantages can be achieved, e.g., the local
processor can be made far less complex than the
global processor?
Discussions about these points have been made,
e.g., in (Chong,1979; Hashemipour & Laub, 1987,
1988; Hassan et al., 1978; Mutambara, 1995;
Quirino et al., 1998; Quirino & Bottura, 2001;
Sanders et al., 1978; Shah, 1971; Speyer, 1979;
Tackers et al., 1980; and Willsky et al., 1982).
In principle, (7) and (10) can be seen as global
solutions to the hierarchical state estimation problem
based on the dichotomy among the information filter
and the state space Kalman filter representations.
Using (7) and (10) as starting points, a synthetic
diagram proposed as support to the development of
distributed structures is shown in Fig. 2.
The fully connected topologies resulting from the
strictly computational heterarchization of the
Kalman filter, as investigated in (Mutambara, 1995)
and (Quirino et al., 1998), produce optimal
distributed state estimators, due either to the
distribution of the coordinator task into the
subsystems at the lower level in the hierarchy, class
4 of Fig. 2., or to the complete transfer of the whole
coordinator task to the lower level in the hierarchy,
class 3 of Fig. 2., respectively.
Such procedures of heterarchization are
characterized by being merely derived from the
computational distribution of the hierarchical
algorithm on the distributed environment.
In spite of not providing significant gain, the
distributed topologies achieved by purely
computational procedures present important
comparative characteristics to be analyzed and
compared as scalability, communication,
computation, and vulnerability to losses of
communication channels.
DECOMPOSITIONS OF HIERARCHICAL STATE ESTIMATION STRUCTURES - Problems and Strategies
129

Figure 2: Classes of Strategies for Heterarchical Distributed State Estimation
Distribution strategies based on the multiple
projections method as well as on matrix partitioning,
lead us to face the question on which model of the
local subsystems to adopt considering the global
model?
For distributed filters derived via matrix
partitioning and the successive orthogonalizations,
the nodal transformation matrices, under certain
assumptions, can be implicitly modeled in such a
way that, the local estimates can be considered very
close to the optimal estimation. This approximation
transforms such structures, in principle strongly
coupled into structures partially decoupled of
optimal state estimation.
Strongly coupled topologies provide a very
restricted practical utilization when dealing with
large scale systems. Within this context,
generalizations of the state space model as well as of
the form how the nodal transformation matrices are
obtained, are essential to develop topologies of state
estimation weakly or strongly decoupled state
estimation.
In (Quirino et al.,1998) an heterarchical
distributed estimation topology nonhierarchical,
however fully connected, is proposed.
In spite of the developed structure to be fully
connected, the communication and synchronization
characteristics and the efficiency of the
multiprocessing system were substantially improved.
A variance another transformation, a variant of
the one obtained in (Quirino et al.,1998), is under
investigation using a methodology of nodal
transformation proposed in (Mutambara,1995).
The development of distributed state estimation
structures expliciting its correlations only in a
heuristic way encumbers an enlarged understanding
of the relationship among that structure and the
existing ones.
Opposite to this perspective, in (Quirino &
Bottura,2001) a suboptimal state estimation structure
is proposed via an analytical development. This
structure is conformed in the class 2 of Fig. 2. of
strategies, and its development is based on the
hierarchical structure proposed in (Hassan et
al.,1978). This analytical development and the form
of the approximate nodal transformation used in
(Quirino & Bottura,2001) based on the SPA
(Supplementing Partitioning Approach) technique
proposed in (Shah,1971). Also, in (Quirino &
Bottura,2001) a theorem that establishes the
necessary and sufficient conditions to obtain the
heterarchical distributed structure is presented, as
DICHOTOMY OF THE
DISTRIBUTED
MODELLING
NODAL
TRANSFORMATIONS T
i
1
2
3
4
INFORMATION
FILTER
KALMAN
FILTER
Sucessive
Orthogonalizations
Matrix
Partitioning
β
η
Suboptimal
Heterarchical
State Estimation
Structures
Optimal
Heterarchical
State Estimation
Structures
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
130

well as for the analysis of the conditions
heuristically established in (Shah,1971).
Filters conformed in the class 1 of Fig. 2., should
be investigated using the same approximate
representation used in (Quirino & Bottura,2001).
A study of canonical forms of the nodal
transformation matrices, indispensable to formulate
the distribution strategies, would be of great value to
the design and analysis of distributed efficient
structures for the estimation problem.
It is important to highlight that within the context
of prospects for future investigations and discussion
on the design of distributed state estimators,
(Willsky et al.,1982) remains one of the most
important references.
5 CONCLUSIONS
In addition to presenting some strategies to construct
distributed state estimation algorithms proposed in
the literature analyzing some aspects of them, we
discuss an heterarchical distributed state estimation
algorithm proposed in (Quirino & Bottura,2001).
It is our belief that the material presented in this
paper contributes to the development of efficient
distributed state estimation algorithms.
REFERENCES
Anderson, B. D. O. and Moore J. B., 1979. Optimal
Filtering, New Jersey.: Prentice Hall, pp. 138-142.
Chong, C.Y., 1979. Hierarchical Estimation, Proc.2
nd
MIT
/ONR C
3
Workshop, Monterey, CA.
Hashemipour, R. H. and Laub, A. J., 1987. Decentralized
Structures for Kalman Filtering. IEEE Trans. on
Automatic Control, vol. 33, pp. 88–94.
Hashemipour, R. H. and Laub, A. J., 1988. On the
Suboptimality of a Parallel Kalman Filter. IEEE Trans
on Automatic Control, vol. 33, pp. 214–217.
Hassan, M. F., Salut, G., and Singh, M. G., 1978. A
Decentralized Computational Algorithm for the Global
Kalman Filter, IEEE Trans. on Automatic Control,
vol. 23, pp.262-268.
Kalman, R. E., 1961. New Results in Linear Filtering and
Prediction Theory, Basic Engineering. J., pp. 95-107.
Mutambara, A.G.O., 1995. Decentralized estimation and
Control with Application to a Modular Robot, Ph.D.
Thesis, Oxford University, UK.
Quirino, R.B., Bottura, C.P., and Costa Filho, J.T., 1998.
A Computational Structure for Parallel and Distributed
Kalman Filtering, 12o. Congresso Brasileiro de
Automática, Uberlândia, MG, Brazil.
Quirino, R.B. and Bottura, C.P., 2001. An Approach For
Distributed Kalman Filtering, Revista Controle &
Automação da Sociedade Brasileira de Automática,
vol. 12, pp.19-28.
Sanders, C.W., Tacker, E.C., and Linton, T.D., 1978.
Specific Structures for Large Scale State Estimation
Algorithms Having Information Exchange, IEEE
Trans on Automatic Control, vol. 23, pp. 255-260.
Shah, M.M., 1971. Suboptimal Filtering Theory for
Interacting Control Systems, Ph.D..Thesis, Cambridge
University, UK.
Speyer,J.L., 1979. Computation and Transmission
Requirements for a Decentralized Linear Quadratic
Gaussian Control Problem, IEEE Trans .on Automatic
Control, vol. 24, pp. 266-269.
Tacker,E.C., Sanders,C.W.,1980. Decentralized Structures
for State Estimation in Large Scale Systems, Large
Scale Systems, Vol. 1, pp. 39-49.
Travassos,Travassos, R.H., 1983. Application of Systolic
Array Technology to Recursive Filtering, Ed. Thomas
Kailath, New Jersey: Prentice Hall, 1983, pp.375-388.
Willsky, A.S., Bello, M.G., Castanon, D.A., Levy, B.C.,
Verghese, G.C., 1982. Combining and Updating of
Local Estimates and Regional Maps Along the Sets of
One Dimensional Tracks, IEEE Trans. on
Automatic Control, vol. 27, pp. 799-813.
Talukdar, S., Ramesh, V.C., Quadrel, R., and Christie, R.,
1992. Multiagent Organization for Real Time
Operations, Proc. of the IEEE, vol. 80, N. 5, pp. 765-
778, May.
DECOMPOSITIONS OF HIERARCHICAL STATE ESTIMATION STRUCTURES - Problems and Strategies
131