
SYSTEMATIC APPROACH TO MODEL-BASED DATA SURVEY
Ari Isokangas, Mika Ruusunen and Kauko Leiviskä
University of Oulu, P.O.Box 4300, 90014 University of Oulu, Finland
Keywords: Identification, Input selection, Characterisation, Model construction, Process control.
Abstract: A framework for surveying multivariate process data is prese
nted. Systematic procedure utilises linear
model candidates constructed in sliding data windows of varying length, to determine the usefulness of data
segments for process identification. The discussed survey approach was applied to an industrial wood
debarking data, enabling the study of process variables and conditions affecting the wood losses. In
addition, main process interactions and delays were easily discovered from the structures of the interpretable
linear model candidates. The analysis can thus provide valuable information also for process modelling and
control.
1 INTRODUCTION
Information retrieval from data is the first and
crucial step in order to obtain knowledge for process
identification. At this stage, one wants to point out
the usefulness and possible problem areas of data
(Pyle, 1999). This, in turn, requires that a
representative sample of the population is available,
for example, applying the design of experiments
(DOE). However, industrial data sets are often in
large databases incorporating all the unmeasured
disturbances and changing operating conditions. In
these cases, data analysis via trial and error can be
laborious. This paper describes an approach to
survey data with a systematic model-based
procedure.
A typical example of process d
ata that is difficult
to analyse, is data from the wood debarking process
in pulp and paper mills. There the costs of raw
material play an important role in the plant
economy. In the debarking process, 1-3% of raw
material goes as wood losses to the combustion
process with bark. The analysis of process and
determining the process parameters to minimise
wood losses may result in annual savings of
hundreds of thousands of euros.
Isokangas and Leiviskä (2005) modelled wood
lo
sses of drum debarking without any special
emphasis on training data selection. Näsi et al.
(2001) used data clustering, but in both cases
analysis was not very successful. It was concluded
that this was partially due to inaccurate and
insufficient measurements of the debarking drum.
There was not, for example, any measurement for
the quality of raw material, which had a strong effect
on the process state. Also, wood loss data contained
a lot of process malfunctions and unmeasured
changes in operation conditions. The selection of
information rich data for modelling is important and
it can only be obtained with a proper data survey. In
this context, data survey means identifying general
properties of process relationships in data, leading to
the preliminary analysis of data for modelling.
There are studies concerning the length of
t
raining data to the performance of models.
Correctly selected training data incorporates
essential information about the phenomenon to be
modelled and models constructed with such data
worked well (Anctil, Perrin & Andréassian, 2004;
Kocjančič & Zupan, 2000). In this view, the main
idea of the presented approach is the procedure to
systematically search for information rich data
segments. For this purpose, it uses sliding windows
across a data set and varying window sizes. Locally
focused data analysis with windowing makes it also
possible to use linear techniques.
There are also many reported model structure
i
dentification methods, for example sliding data
window approach (Luo & Billings, 1995), fuzzy
cluster analysis (Šindelář, 2004; Abonyi, Babuška &
Feil, 2003), a modal symbolic classifier (Prudêncio,
Ludermir & de Carvalho, 2004), combined forward
and exhaustive search (Mendes & Billings, 2001),
including partly automated data pre-processing and
60
Isokangas A., Ruusunen M. and Leiviskä K. (2005).
SYSTEMATIC APPROACH TO MODEL-BASED DATA SURVEY.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 60-65
DOI: 10.5220/0001165600600065
Copyright
c
SciTePress

identification method (Simon, Schoukens & Rolain,
2000). Other authors report also studies utilising
self-organising networks (Linkens & Chen, 1999)
and fuzzy algorithm for model structure
identification (Sugeno & Kang, 1988).
Abovementioned investigations have their focus
mainly on the automatic model input, order or
parameter selection. Unfortunately, only a few
researches deal with systematic data survey, for
example in the form of entropic analysis (Pyle,
1999), which covers issues needed for process
identification in all respects.
The approach in this paper intends to combine
necessary aspects for systematic data survey,
namely: providing easily interpretable results
without the need for complex pre-processing, and
systemising search of representative process
conditions in large databases. The method constructs
automatically linear dynamic model candidates,
from all available input combinations in every data
window examined. The final analysis concerns then
with the model structure properties of the best
candidate models. The performance assessment of
the models uses the root mean square error (RMSE)
values, correlation coefficients and the visual
appearance of the model behaviour.
The following sections introduce the framework
for model-based data survey and apply it to wood
loss data from a pulp mill. The paper concludes with
the analysis and discussion of the results
2 MODEL-BASED DATA SURVEY
APPROACH
2.1 Overview
The aim of the discussed data survey procedure is to
find interactions between variables from large
datasets. This occurs systematically by constructing
simple dynamic model candidates with complete
input combinations for data segments of varying and
sliding window size. The final analysis goes on
according to the model structure properties of the
best candidate models.
Linear model structure was chosen as a
candidate. Model simplicity guarantees the
modelling efficiency, because of the great number of
constructed and tested models. The theory of
estimating model parameters is well defined in the
literature (see Ljung, 1999; Söderström & Stoica,
1988). The structure of a dynamic ARX-model is
A(q)y(t) = B(q)u(t-nk) + e(t) , (1)
where A(q) defines the number of poles (how many
output values are used), B(q) is the number of zeros
(how many previous inputs are used), nk is the delay
and e the noise term.
AR-models are the special cases of ARX-
models, where no poles and no delays are used and
the number of zeros is one. AR-models are static
models, which are also called linear regression
models. These models are normally estimated using
the least squares method. AR-models require less
computation power and apply therefore to the search
of significant process variables.
Model candidate construction, validation and
testing proceed in the following way: the half of all
available data is used in training and validation so
that model candidates are constructed systematically
from the beginning of data with selected data
window size. After each data window has been used
for training, the window of same size is taken for
validation. The procedure uses a partly overlapping
data window. For example, if the data window is
400 minutes, first models are constructed using
training data from 1 - 400 minutes and data from
401 - 800 for validation of a model candidate under
evaluation. Next, all model candidates are
constructed using training data from 201 - 600 and
validation data from range 601 - 1000 minutes. To
define the right size of training data, different
window sizes are systematically tested at this stage.
Models are evaluated with the correlation coefficient
and RMS-error measure using validation data. Best
models are further tested with independent testing
data, which is another half of available data.
The data survey starts from M observations of
one output variable and N input variables.
11
1
22
1
1
...
...
... ... ... ...
...
N
N
1
2
M
MM
N
yx x
yx x
yx x
Step 1: Select the size of the time window, M1,
for training and validation. There are two choices:
Start with a small window size and extend it during
the survey, or start with M1=M/2 and decrease it.
Step 2: Select the data range for training and
validation. During the first iteration, choose the
observations m=1…M1 for modelling and
m=M1+1…2M1 for validation. If there are still
observations left, during the next iteration choose
SYSTEMATIC APPROACH TO MODEL-BASED DATA SURVEY
61

observations m=M1/2+1…1.5M1 for modelling and
m=1.5M1+1…2.5M1 for validation. Use this
overlapping sliding window for all observations.
Step 3: Select the input combination for
modelling. For example, from 15 input variables
using two inputs results in totally 105 combinations,
using 3 inputs 455 and using 4 inputs 1365 different
input combinations. After this, the structure
information of candidate models is stored in tables.
This phase of work is necessary in order to define
inputs that explain most of the output variation. In
the following steps, only inputs proved to be
important are selected for further analysis.
Step 4: Construct the model. All input
combinations are applied one by one in every data
window to model the selected output. At this stage,
only static AR-models are utilised to get
computation less demanding.
Step 5: Test with validation data. If all input
combinations and the whole data range are tested, go
to the next stage. If not, go either to Step 3 or Step 2.
Step 6: Store the best models for testing with
independent data. Best model candidates are stored
in tables, with the root mean square error (RMSE)
and correlation coefficient values of training,
validation and testing data, data range used for
training, variables in models and model degrees (see
for example Table 1). This way it is possible to
reconstruct individual models for further use or
graphical inspection. Model parameters are not
stored in tables, but they can be easily retained on
the basis of table values. All the needed information
for the data survey is then available in result tables.
Step 7: If all window sizes are analysed, the
procedure ends. If not, go to Step 1.
The main stages of the presented data survey
approach are described in Fig. 1.
Figure 1: Flowchart of the data survey approach
Using all the previous phases and input variable
combinations, hundreds of thousands of model
candidates can be constructed and tested. This would
be impossible without the described systematic
procedures.
The data survey method was programmed using
MATLAB® script language and functions in
MATLAB® identification-toolbox. Data survey was
performed with software that makes use of the
collected data sets.
3 RESULTS
Analysis of data from an industrial wood debarking
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
62
process was used as a case example to show the
effectiveness of the discussed approach.
3.1 Industrial Wood Debarking
Process
In debarking process, logs are debarked in a drum;
typical dimensions are 5 m of diameter and length of
30 m. Logs scrub each other in the drum and bark is
separated from logs. Bark is removed from the drum
via bark holes in the sides of the drum, logs exit
from the end of the drum for further process stages.
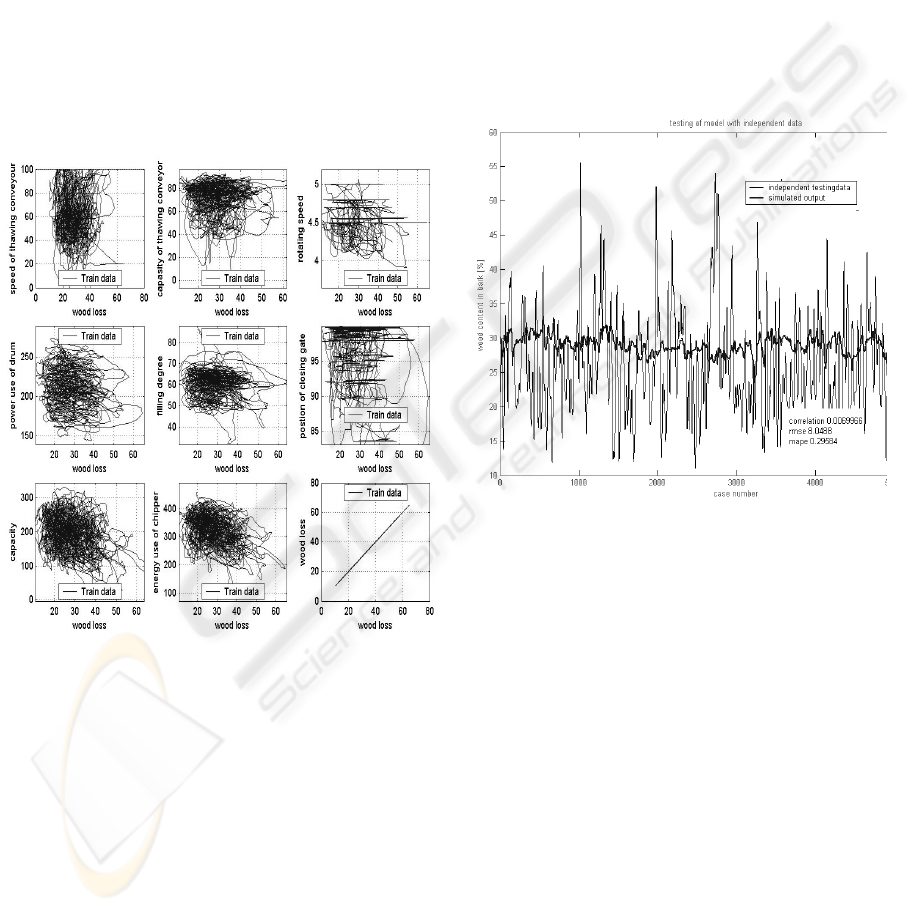
Typical measurements are presented as scatter plots
in Fig. 2 describing the general properties of wood
loss data.
Figure 2: Scatter plot from the measurements of the
debarking drum. Wood loss measurement (output
variable) in x-axis and input variables in y-axis
3.2 Process Identification without
the Data Survey
This section presents a typical example, how linear
model works, if the systematic data survey is not
used.
First, all available measurements of debarking
plant were investigated using cross correlation tables
and graphical presentations. Cross-correlation
analysis was committed for measurements, but all
correlations with wood loss measurement (output)
were only between 0 – ±0.4. Correlation describes
only a linear dependency, so graphical analysis was
the next step.
It was noted that there were no remarkable
dependencies between process measurements and
wood losses (Fig. 2). This was mainly because data
set from a large database incorporated a lot of
different operation conditions. Scatter plot figures
show that modelling wood loss without any
systematic modelling approach will be difficult.
Preliminary identification tests with linear
models showed unsatisfactory results (Fig. 3), when
training data set was selected randomly. In this case,
first 25 % of the data is used for training, next 25%
for validating and the rest 50% for testing.
Figure 3: Comparison of simulated wood losses with
measured data, when training data has been selected
without a prior analysis
3.3 Data Survey with the Model-
based Approach
In this section an example of the data survey is
given. Results were obtained through simulations
with the validation data set.
The procedure described in section 2 provided
the following results: first using four inputs gave
better modelling accuracy for candidates than two or
three. Modelling with five inputs was committed
also later, but the results were not as good as for four
inputs. The parameters used for constructing models
and model goodness values are in Table 1 for some
of best models gained using data survey. The
optimal size of data window for training data
seemed to be quite short, typically from 100 to 400
minutes. Candidate models constructed using the
window sizes of 500-1000 usually failed. From the
SYSTEMATIC APPROACH TO MODEL-BASED DATA SURVEY
63

result table one can conclude that some segments of
data seemed to be good for training data whereas
some areas contained malfunction data and models
constructed with such data failed. The best model
candidates were selected on the basis of root mean
square error (RMSE), correlation values and visual
appearance of the model behaviour. According to
the result table, the best variables describing wood
losses were (1) rotating speed of the drum, (2) the
filling degree, (3) capacity and (5) the position of
closing gate. This agrees well with the operator
experience from the process.
Table 1: Some of the best candidate models gained
utilising data survey
Fig. 4 presents simulation results with
independent testing data, when training data has
been selected automatically (row 1 from Table 1).
Figure 4: Testing wood loss model with independent
testing data, when training data has been selected in the
systematic way
Fig. 5 shows the main process interactions found
after the data survey for four variables that effect to
wood loss of debarking process. For example,
increase in capacity clearly seems to decrease the
wood loss. The relationship between these variables
is similarly recognised by process operators.
4 DISCUSSION
Fig. 2 shows at the first glance that there are no
dependencies between wood loss and input
variables. Modelling with such data will be difficult
as can be seen from Fig. 3, although all the input
combinations were tested. This is because training
data was too large containing too many different
process conditions and changes in the quality of raw
material.
Fig. 5, on the other hand, shows that the data
survey finds the main process interactions. This
suggests that the selection of correct inputs, optimal
data window sizes and optimal data segments
reveals clear interactions between variables. This
may in turn give acceptable results even with very
simple modelling techniques (Fig. 4). Model
development can continue after this with more
sophisticated models.
Rotating speed
Filling degree
Figure 5: Main process interactions according to the data
survey
The optimal size of data windows might vary
with different modelling methods. Another
challenge in this approach is the need for
computation power. Typical calculation times were
from 30 minutes (AR-models) to 12 hours (approx.
100 000 models constructed, validated and tested).
This can be better coped by implementing
calculations in more powerful servers. On the other
RMSE 7.6
MAPE 0.24
Capacity
Chipper power
Wood content in bar
k
Wood content in bar
k
Wood content in bar
k
Wood content in bar
k
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
64

hand, calculation times with the state of art PC are
also reasonable.
Although the presented approach proceeds
systematically, some expertise is useful defining the
correct boundaries for calculating parameters, for
example, data window sizes. If limits are set too
wide, calculation times may increase exponentially.
In this phase, there is not any automated procedure
to select best model candidates from result table and
requires also expertise. This is mainly because the
selection of best model candidates requires also
visual inspection of the model behaviour and is
therefore difficult to automate. In the future, the
approach will be developed more into fully
automated way.
The presented approach can provide successful
results, even if data pre-processing or outlier
removal has failed. This is because data survey can
help to choose data segments containing only
relevant information. Thus, the need for data survey
is evident.
5 CONCLUSIONS
In this paper, a systematic approach for data survey
was presented and applied to wood loss data.
Model candidates using simple dynamic ARX –
models were constructed systematically with
different input combinations, window sizes and data
ranges. The target was to find out the best data sets
for further modelling. Model candidates working
best with validation data were stored and tested with
independent data.
Main process interactions and delays were easily
discovered from structures of the interpretable linear
model candidates. The analysis can thus provide
valuable information also for the model structure
selection. This shows the importance of proper data
survey. It is also one kind of data mining stage: with
the proper data survey, best inputs, correct
interactions between variables and optimal data
window sizes could be found even with linear
modelling methods. Data survey also provides
information about model degrees and delays. This
kind of knowledge discovery is an important step in
process control development.
REFERENCES
Abonyi, J., R. Babuška and B. Feil, 2003. Structure
selection for nonlinear input-output models based on
fuzzy cluster analysis. IEEE International Conference
on Fuzzy Systems, v 1, pp. 464-469
Anctil, F., C. Perrin and V. Andréassian, 2004. Impact of
the length of observed records on the performance of
ANN and conceptual parsimonious rainfall-runoff
forecasting models, Environmental Modelling &
Software, 19, pp. 357-368.
Isokangas A. and K. Leiviskä, 2005. Minimising wood
losses of drum debarking. Accepted to Paper and
Timber magazine.
Kocjančič R. and J. Zupan, 2000. Modelling of the river
flowrate: the influence of the training set selection,
Chemometrics and Intelligent Laboratory Systems, 54,
pp. 21-34.
Linkens, D.A. and M.-Y. Chen, 1999. Input selection and
partition validation for fuzzy modelling using neural
network. Fuzzy Sets and Systems, 107, pp. 299-308.
Ljung, L., 1999. System identification: theory for the use.
Prentice hall, Englewood cliffs, NJ.
Luo, W. and S.A. Billings, 1995. Adaptive model
selection and estimation for nonlinear systems using a
sliding data window, Signal Processing, 46, pp. 179-
202.
Mendes, E.M.A.M and S.A. Billings, 2001. An alternative
solution to the model structure selection problem.
IEEE Transactions on Systems, Man, and Cybernetics
Part A: Systems and Humans, 31, pp. 597-608.
Näsi, J., A. Isokangas and E. Juuso, 2001. Klusterointi
kuorimon puuhäviöiden mallintamisessa. ISBN 951-
42-5894-0.
Prudêncio, R.B.C., Ludermir T.B. and de Carvalho F.A.T.,
2004. A Modal Symbolic Classifier for selecting time
series models, Pattern Recognition Letters, 25, pp.
911-921.
Pyle, D., 1999. Data Preparation for Data Mining.
Morgan Kaufmann, San Francisco, California.
Simon, G., J Schoukens and Y. Rolain, 2000. Automatic
model selection for linear time invariant systems,
Proceedings of the12th IFAC Symposium on System
Identification, SYSID, Santa Barbara, CA, USA, 21-
23 June 2000, Vol. I., pp. 379-384.
Šindelář, R., 2004. Input selection for fuzzy modelling.
Proceedings of the 2nd IFAC Workshop on Advanced
Fuzzy/Neural Control, Oulu, Finland, pp. 13-18.
Sugeno, M. and G. Kang, 1988. Structure identification of
fuzzy model. Fuzzy Sets and Systems, 28, pp. 15-33.
Söderström, T. and P. Stoica, 1988. System identification,
Englewood cliffs, NJ. Prentice Hall.
SYSTEMATIC APPROACH TO MODEL-BASED DATA SURVEY
65
