
A GENERIC MODEL FOR ESTIMATING
USER INTENTIONS IN HUMAN-ROBOT COOPERATION
∗
Oliver C. Schrempf and Uwe D. Hanebeck
Intelligent Sensor-Actuator-Systems Laboratory
Institute of Computer Science and Engineering
Universit
¨
at Karlsruhe (TH)
Karlsruhe, Germany
Keywords:
Intention-Recognition, Hybrid Dynamic Bayesian Networks, Human-Robot Interaction.
Abstract:
The recognition of user intentions is an important feature for humanoid robots to make implicit and human-like
interactions possible. In this paper, we introduce a formal view on user-intentions in human-machine interac-
tion and how they can be estimated by observing user actions. We use Hybrid Dynamic Bayesian Networks
to develop a generic model that includes connections between intentions, actions, and sensor measurements.
This model can be used to extend arbitrary human-machine applications by intention recognition.
1 INTRODUCTION
An important goal for the design of intelligent user
interfaces for human-machine interaction is to suc-
ceed the mere execution of explicit user commands.
Accepting implicit commands as well as not directly
observable desires of the user are key factors for mak-
ing interactions with robots more appealing and com-
fortable. Humans use implicit clues or estimations of
their partner’s “state of min” in everyday communica-
tion with other humans (Breazeal, 1999). Hence, hu-
manoid robots can gain a lot of acceptance, when co-
operating with them is as intuitive as cooperating with
other humans. In order to achieve this, the user in-
terface must respond to implicit information and pre-
dict hidden, or not directly observable demands of the
user. In other words, the robot must recognize the
user’s intention.
Incorporating information on a user’s intention into
user interfaces opens a wide field of applications.
One of the most popular approaches in recognizing
user intentions is the Lumi
`
ere project of Microsoft re-
search (Horvitz et al., 1998). They use Bayesian Net-
works to estimate the goals of a user.
In this paper we describe the application of Hybrid
Dynamic Bayesian Networks for recognizing user in-
tentions. Hybrid means the simultaneous treatment of
continuous- and discrete-valued states in one model.
Using a hybrid approach is extremely important for
∗
This work was supported in part by the German Re-
search Foundation (DFG) within the Collaborative Re-
search Center SFB 588 on ”Humanoid robots – learning and
cooperating multimodal robots”.
robots operating in real world domains, since both
continuous- and discrete-valued states appear in al-
most every scenario that combines high level action
representations and low level sensor measurements.
Furthermore, we focus on tracking temporally
evolving aspects like successive actions performed by
the user. In order to improve the estimate concern-
ing the hidden intentions, we study the application of
dynamic models.
The remainder of this paper is organized as follows.
Section 2 gives a formulation of the problem to be
solved followed by our idea on how to recognize user
intentions in section 3. In section 4 we give an intro-
duction to Hybrid Dynamic Bayesian Networks. The
generic model we propose for intention recognition
is shown in section 5 followed by an example in sec-
tion 6. Section 7 concludes the paper and gives a short
outlook on future topics.
2 PROBLEM FORMULATION
The intention of a user in general is a hidden state that
cannot be observed directly. Hence, technical systems
like robots have a problem in deciding what the user
really wants them to do, when they are not instructed
explicitly via remote control or voice commands. An
example for this is a household assistant robot that
carries a pot of tea. If the user carries a tray with a
cup on it, the robot has to decide whether the user
wants some fresh tea in his cup or if the pot has to be
put on the tray.
On the other hand, user actions are recognizable
251
C. Schrempf O. and D. Hanebeck U. (2005).
A GENERIC MODEL FOR ESTIMATING USER INTENTIONS IN HUMAN-ROBOT COOPERATION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 251-256
DOI: 10.5220/0001166002510256
Copyright
c
SciTePress

(not hidden), since they produce observable events.
These observable events may stem from all imagin-
able modes of human communication. They involve
verbal, as well as non-verbal modalities like gestures
or facial expressions.
The task is to find a model that characterizes the hu-
man user, based on his/her intentions, while consider-
ing the actions a user can perform as a consequence
of these intentions. This is called a forward model,
since it covers only causal dependencies, namely the
dependency of actions upon intentions.
3 RECOGNIZING INTENTIONS
FROM ACTIONS
We address the recognition of user intentions as an al-
gorithmic reasoning process that infers hidden inten-
tions from observed actions. Since observations made
by a robotic system, as well as the correlation between
intentions and actions suffer from uncertainties, we
propose the application of a probabilistic model.
Hidden Markov Models (HMM) are well known
stochastic models for collecting information se-
quences over time in order to make estimates on hid-
den states (Rabiner, 1989). Unfortunately, they pro-
vide only a relatively simplistic way for describing
causal structures. More sophisticated models are pro-
vided by autoregressive HMMs or factorial HMMs.
The first kind treats the dependency between suc-
cessive measurements, whereas the second kind is
concerened with multiple sequences of hidden states
jointly causing a common measurement.
All these models (HMM, AR-HMM, and factor-
ial HMM) can be viewed as members of the Dy-
namic Bayesian Networks family (DBN) (Roweis and
Ghahramani, 1999). DBNs of arbitrary structure pro-
vide a higher flexibility in modeling than generic
HMMs, since they exploit the causal dependency
structure of the given domain.
In literature DBNs are often limited to discrete-
valued domains (Korb and Nicholson, 2003) and hy-
brid Networks are only considered for special cases
(Murphy, 2002). It is obvious, that the domain of
human-robot interaction can only be described by a
joint set of continuous and discrete variables. Sen-
sor measurements and the corresponding probabilis-
tic models for example rely heavily on physical laws
that are based on continuous scales like meters, de-
grees, and so on. Higher level or semantic aspects of
human behavior are often expressed by discrete vari-
ables. Hence, hybrid DBNs are very important for
intention recognition in human-robot cooperation.
In this paper we present a new approach for
user intention recognition based on Hybrid Dynamic
Bayesian Networks. The proposed approach uses
Gaussian mixture densities, i.e. sums of weighted
Gaussian densities, to describe continuous uncertain-
ties. Discrete uncertainties are described by sums of
weighted Dirac pulses.
4 BAYESIAN NETWORKS
Bayesian Networks are considered to be an effi-
cient representation of joint probabilities, exploit-
ing causal dependencies in a domain (Pearl, 1988).
This is achieved by representing the causal depen-
dency structure of a domain by means of a directed
acyclic graph (DAG). Each variable in such a domain
is depicted by a node in this graph and every edge
stands for a direct dependency between two variables.
Hence, this graph is often referred to as dependency
graph. The dependency between two variables x and
y denoted by an edge from node x to node y is mod-
elled by a conditional probability function f (y|x).
Since the direction of the edge represents the causal
dependency of y upon x, we call this a probabilistic
forward model. To describe the joint probability of all
variables in the system, not all possible combinations
of variables and their states have to be addressed. It
is sufficient to consider the conditional probability for
each variable given its parents in the graph.
The first Bayesian network models were limited to
discrete valued domains and their likelihood functions
were given by conditional tables. The most common
approach for evaluating discrete networks by means
of message passing (Pearl, 1988). In this approach
observations or measurements are incorporated into
the according nodes. These nodes send message prob-
abilities to their adjacent nodes, depending on the
modeled conditional probabilities. In this way the in-
formation travels through the network.
This approach was extended to continuous net-
works (Driver and Morrell, 1995), where Gaussian
mixtures were used to approximate the conditional
density functions and to represent the messages trav-
eling through the network.
Hybrid Bayesian networks today consider often
only linear dependencies by using so called cg-
potentials (Lauritzen, 1992). Nonlinear dependencies
cannot be covered in this type of model The treatment
of nonlinear dependencies between variables requires
more complex density representations than offered by
cg-potentials. Approximating the conditional density
functions by means of Gaussian mixtures is a well
known approach (Driver and Morrell, 1995). We ex-
tended this approach tow hybrid domains (Schrempf
and Hanebeck, 2005). Since this is the approach we
propose for intention recognition, we give a short in-
troduction in the next subsection.
ICINCO 2005 - ROBOTICS AND AUTOMATION
252

X
X
Q
X
Q
X
P
[
\
\
Q
\
Q
\
P
(a) continuous case
X
X
Q
X
Q
X
P
\
\
Q
\
Q
\
P
[
(b) discrete case
Figure 1: The simultaneous treatment of continuous and
discrete variables requires the consideration of two distinct
cases. The nodes in box shape are discrete, whereas the
continuous nodes have a round outline. Hence, a) shows
the continuous case and b) the discrete case.
4.1 A Hybrid Bayesian Network
Every node in the network stands for a random vari-
able that can be either continuous or discrete. This is
shown in figure 1. The nodes in box shape are dis-
crete, whereas continuous nodes have a round out-
line. Every edge from a node x to a node y in
the graph stands for a conditional density function
f(y|x). The simultaneous treatment of continuous
and discrete variables used in our approach requires
the consideration of two distinct cases, which are
shown in figure 1. For the parent nodes u
1
,...,u
m
and the child nodes y
1
,...,y
m
we assume a partition
into continuous (u
1
,...,u
n
or y
1
,...,y
n
) and dis-
crete (u
n+1
,...,u
m
or y
n+1
,...,y
m
) variables.
Hybrid Bayesian Networks require hybrid condi-
tional density functions to capture the relationship be-
tween continuous and discrete variables. These den-
sities describe the probability of a continuous or dis-
crete random variable, depending on the state of a
set of mixed parent variables. Mixed means the set
of parent variables contains continuous and discrete
variables as well. We defined a hybrid conditional
density in (Schrempf and Hanebeck, 2004) as
f(x|u
1
,...,u
m
)=
|u
n+1
|
k
n+1
=1
...
|u
m
|
k
m
=1
m
i=n+1
δ(u
i
− k
i
)
f
∗
(x|u
1
, ..., u
n
).
This formulation contains one single continuous con-
ditional density f
∗
(x|u
1
, ..., u
n
) for each joint dis-
crete state (u
n+1
,...,u
m
) of x’s discrete predeces-
sors. The asterisk is an abbreviation in order to indi-
cate the dependency on (k
n+1
,...,k
m
). The number
of states of a discrete variable is indicated by |u
i
|. δ(·)
denotes the Dirac delta function.
In the continuous case the conditional density
f
∗
(x|u
1
, ..., u
n
) is modeled by means of Gaussian
mixtures. We use axis-aligned Gaussian, which
means we have one Gaussian component for each
continuous parent variable and another Gaussian
component for x given by
f
∗
c
(x|u
1
,...,u
n
)=
M
∗
j=1
α
∗
j
N(x, µ
∗
x,j
,σ
∗
j
)·
N(u
1
,µ
∗
u
1
,j
,σ
∗
u
1
,j
) · ...· N(u
n
,µ
∗
u
n
,j
,σ
∗
u
n
,j
),
where N (x, µ, σ) is a Gaussian density over x with
mean µ and variance σ. In the discrete case we use
sums over weighted Dirac pulses
f
∗
d
(x|u
1
,...,u
n
)=
M
∗
j=1
α
∗
j
⎛
⎝
|x|
l
j
=1
p
∗
l
j
δ(x − l
j
)
⎞
⎠
·
N(u
1
,µ
∗
u
1
,j
,σ
∗
u
1
,j
) · ...· N(u
n
,µ
∗
u
n
,j
,σ
∗
u
n
,j
).
The formulae for message passing in a hybrid
Bayesian Network of this kind are given in (Schrempf
and Hanebeck, 2005).
4.2 Dynamic HBNs
So far, we only considered static HBNs as we ne-
glected the temporal behavior of the network. To
capture the evolution of a network over time we use
Dynamic Bayesian Networks (DBNs) as proposed in
section 3. DBNs are time-discrete models, represent-
ing the network at several time-steps while connecting
the network of time-step t with the network in step
t+1 via edges pointing from t to t+1. The edges con-
necting two time-steps represent the transition model
known from HMMs or linear dynamic systems.
Whenever we use discrete and continuous valued
variables in a DBN simultaneously we call it a Hybrid
Dynamic Bayesian Network (HDBN). The process-
ing scheme for HDBNs that we propose for intention
recognition is described in section 5.3.
5 INTENTION RECOGNITION
In this section we present a generic HDBN model
to be applied to intention recognition. The model is
shown in figure 2. The shape used for the represen-
tation of the nodes indicates that every node can be
of continuous or discrete type. Hence, the network is
hybrid. We first consider the part of the model that
is time invariant. We call this part the causal intra-
time model. It includes all solid black edges in one
time-step of figure 2.
User intentions are often influenced by external cir-
cumstances. In other words, the intention is affected
by the environment the user acts in. We cover these
environmental influences by a node containing “do-
main knowledge”. This knowledge can be given in
A GENERIC MODEL FOR ESTIMATING USER INTENTIONS IN HUMAN-ROBOT COOPERATION
253

,QWHQWLRQ
DFWLRQ
GRPDLQ
NQRZOHGJH
PHDVXUHPHQW
PHDVXUHPHQWP
DFWLRQQ
PHDVXUHPHQW
PHDVXUHPHQWP
,QWHQWLRQ
DFWLRQ
GRPDLQ
NQRZOHGJH
PHDVXUHPHQW
PHDVXUHPHQWP
DFWLRQQ
PHDVXUHPHQW
PHDVXUHPHQWP
WLPHVWHSW WLPHVWHSW
Figure 2: The generic HDBN model for intention recognition features one node for the hidden intention state in every time
step. Possible actions are given as nodes depending on the intention. The outline of the nodes denote that they are of
continuous or discrete type (hybrid network).
one node or be split into several nodes, when the
pieces of information are independent. It is also pos-
sible to have a full-featured Bayesian subnetwork to
reason about the domain. In this case it is only im-
portant that the dependency of the intention on this
domain is given in the model.
The hub of the subnetwork at every time step, al-
though not the root node, is a node that stands for the
user’s intention. This is a hidden state, which can-
not be observed directly. For most applications, this
node is discrete, since there are distinct intentions that
need to be distinguished. Nevertheless, it is possible
to define continuous intentions, since we are using a
hybrid network. This is useful when the user intention
is a specific adjustment on a continuous scale, for ex-
ample a desired temperature.
A user performs actions depending on the inten-
tion. These actions do not depend on other actions in
the same time step. This does not mean that these ac-
tions are mutually exclusive! The key point here is,
that the actions depend causally on the intention and
not vice versa. We cover this fact by the application
of a probabilistic forward model f (action
i
|intention)
for every known action
i
. Due to the power of prob-
abilistic reasoning we are able to infer the intention
from information on performed actions.
Humans seem observe actions of other humans di-
rectly, although they may fail in some cases. This is
due to the fact that observation is a cognitive process,
which is based on sensory stimuli. Robots, have to
reconstruct observations from sensor measurements,
too. Hence, we need an additional layer (measure-
ment nodes) in our network. Here we can apply stan-
dard measurement models known from dynamic sys-
tems theory.
The temporal part of our model is called the causal
inter-time model. This comprises the dashed grey
edges in figure 2 pointing from time-step t to time-
step t+1.
To represent temporal behavior of a user, we intro-
duce an edge from the intention node in time-step t to
the intention node in time-step t+1. This enables us to
cope with a user “changing his/her mind”.
Actions may depend on the actions performed in
the preceding time step. Hence, an edge from every
action to its corresponding node in the next step is
drawn. These edges contain information on how
likely it is, that the same action is performed twice,
given a certain intention. Edges from one action in
times step t to a different action in time step t+1 are
possible as well, introducing information on the like-
lihood of successive actions.
Since sensor measurements depend only on the ac-
tion at the current time step and not on previous mea-
surements, no edges are drawn from a measurement
in time step t to the corresponding measurement in
time step t+1.
5.1 Model Structure
Most aspects of the structure of the described model
are predefined. There are only a few structural deci-
sions to be made when applying the model to a spe-
cific scenario.
1. The intentions to be recognized must be chosen.
They are modeled as states of the intention vari-
able.
2. A model for the domain knowledge must be given
as described above.
3. The possible actions of the user must be added,
each with an appropriate measurement model.
ICINCO 2005 - ROBOTICS AND AUTOMATION
254
d
t
Unit Delay
i
t−1
i
t
Unit Delay
f(a
t
|a
t−1
, i
t
)
a
t
a
t−1
v
t
m
t
g()
a
t
f(i
t
|i
t−1
, )
d
t
Measurement
Model
Figure 3: Block diagram of intention forward model.
5.2 Model Parameters
The parameters of the model govern the conditional
probability functions characterizing the dependency
between the variables. In general there are two ways
of obtaining parameters.
1. An expert can model the parameters “by hand”.
The parameters are then manually adjusted to rep-
resent the expert’s knowledge of the dependency
between the variables.
2. The parameters can be “learned” from observed
training data for example with the Expectation-
Maximization algorithm (EM) (Poland and
Shachter, 1993).
One of the big advantages of the presented model
is that small parts can be modeled independently. For
instance, the possible actions are independent of each
other. They only depend on the intention. This pro-
vides the flexibility to mix expert models and learned
models. It is also possible to add (learn) new actions
without altering the whole network.
5.3 The Estimator
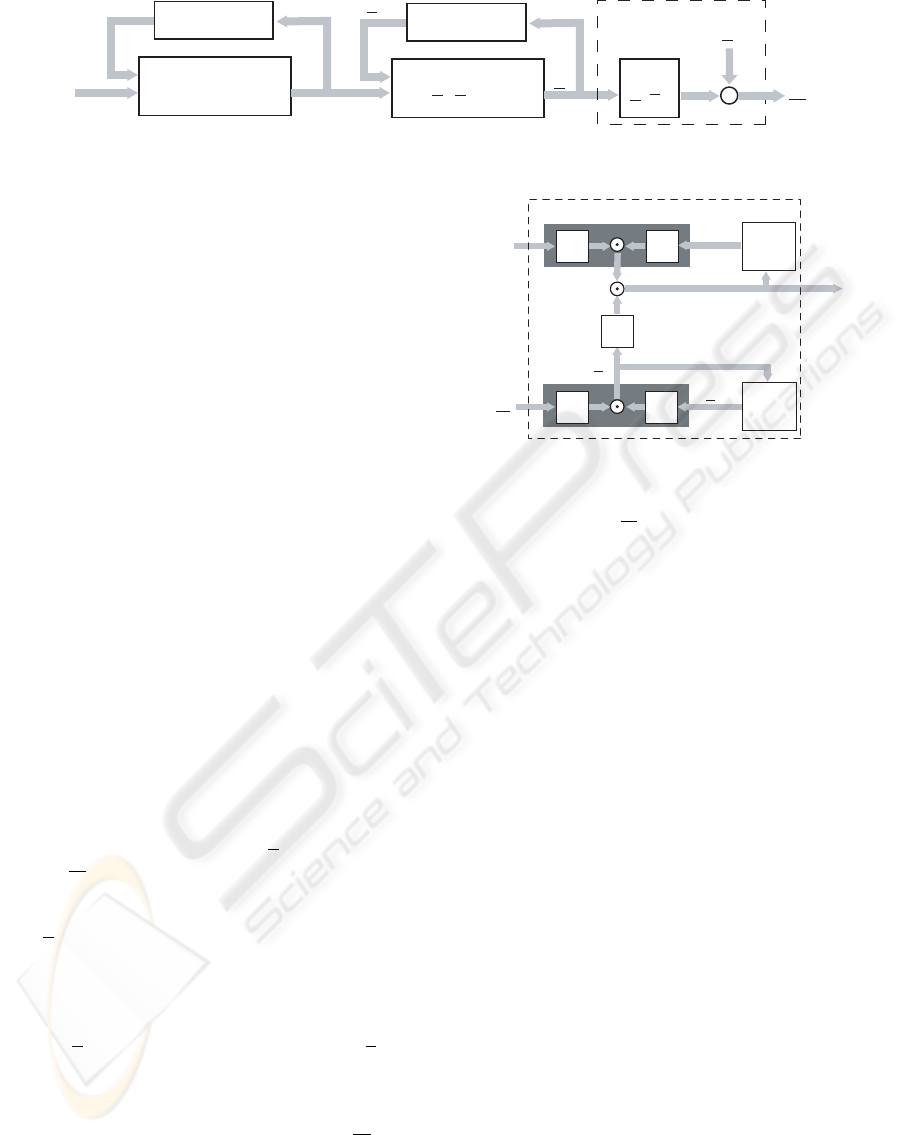
To explain the intention estimator, we introduce an
alternative way of describing our model. A block di-
agram representation is shown in figure 3. In this di-
agram i
t
is the intention variable, a
t
a vector of ac-
tions, and m
t
is the measurement vector. The domain
knowledge is given by the variable d
t
. The first and
the second block contain the conditional densities for
i
t
and a
t
. The vector representation of actions was
chosen just for convenience. Since the actions are in-
dependent they could be modeled by multiple sepa-
rate blocks. The dashed box at the end describes a
standard measurement model for actions with addi-
tive noise v
t
. If the measurement function g(a
t
) is
not known, the dashed block can be subsumed by a
conditional density block like the first two.
The estimator computes a probability density over
the intention i
t
given the measurement vector ˆm
t
and
the domain knowledge
ˆ
d
t
. A graphical representa-
tion is given in figure 4. The BF- and BB-blocks de-
pict a Bayesian forward and Bayesian backward infer-
ence respectively. In this way the density f(i
t
) is cal-
culated via intermediate densities f (a
t
), f
1
(i
t
), and
ˆm
t
ˆ
d
t
BB BF
Unit
Delay
BFBF
Unit
Delay
Estimator
BB
f(i
t
)
f
1
(i
t
)
f
2
(i
t
)
f(a
t
)
f(i
t−1
)
f(a
t−1
)
Figure 4: The estimator computes a probability density over
the intention i
t
based on the current domain knowledge d
t
and the measurements m
t
via intermediate densities f(a
t
),
f
1
(i
t
), and f
2
(i
t
). It consists of Bayesian forward (BF) and
Bayesian backward (BB) inference blocks.
f
2
(i
t
).
The intermediate densities are multiplied, which is
indicated by the dot in the circle. The dark blocks in-
dicate the fusion of information from time-step t with
information from time-step t−1. This is to emphasize
the fact that prediction- and filter-step are processed
simultaneously.
6 EXAMPLE
The generic HDBN model can be used in many sce-
narios. For implementing the model for a real robotics
application, the first step consists in finding the possi-
ble user intentions to be recognized and the actions a
user can perform concerning these intentions. The in-
tentions and actions build the backbone of the HDBN.
In addition it has to be decided, whether the corre-
sponding random variables are continuous or discrete.
In the next step the likelihood functions for the ac-
tions given the intention are assigned. This can be
done by hand when expert knowledge is available, or
data driven methods have to be used as pointed out
above.
The measurement nodes for every action have to
be modeled according to the available sensors. For
a technical system like a robot, user actions are hid-
den states as well. Hence, a measurement model is
required. Figure 5 shows an example for an intention
A GENERIC MODEL FOR ESTIMATING USER INTENTIONS IN HUMAN-ROBOT COOPERATION
255

audio
rooms
intention
take a
plate
open
dishwasher
open
cupboard
user
location
video
laser
scanner
laser
scanner
video
laser
scanner
audio
laser
scanner
Figure 5: Example of an HDBN for a robot assisting in a
household. The robot has to recognize when the user wants
to fill the dishwasher or to lay the table.
recognition HDBN in a household robot scenario. In
this example the robot has to recognize, whether the
user wants to fill the dishwasher or to lay the table.
These intentions are modeled as states of a discrete
intention node. The actions to be observed are the
user opening the cupboard or the dishwasher, when
the user grabs a plate, and the location of the user.
Domain knowledge is incorporated since the intention
depends on the room the user is in. Available sensors
are video cameras, a laser scanner, and an audio sys-
tem.
7 CONCLUSIONS
In this paper a generic model for estimating user in-
tentions by observing user actions has been presented.
Since there is not only one possible sequence of ac-
tions for the user to reach the goal, a stochastic ap-
proach has been chosen to model the relation of in-
tentions, actions, and corresponding sensor measure-
ments. A Dynamic Bayesian Network (DBN) ap-
proach has been proposed for modeling. DBN pro-
vide a flexible way to exploit the causal dependency
structure of arbitrary systems or domains. Due to this
flexibility it is possible to extend the model in local
parts without the need to alter the global model. A hy-
brid DBN (HDBN) has been presented to allow for si-
multaneous treatment of continuous and discrete ran-
dom variables.
The presented model permits to incorporate inten-
tion recognition into arbitrary applications of human-
machine interaction, due to its universality. Estimat-
ing a user’s goals in a graphical user interface on a
computer from tracking mouse actions is possible as
well as a humanoid robot that recognizes user inten-
tions. The model is highly flexible, since it can be
extend very easily. New actions can be added without
touching the whole model. The proposed scheme for
modeling conditional densities even reduces the effort
for adding new recognizable intentions to adding one
conditional density per action.
In the future we will study methods for learning
and adapting the parameters of the model from data.
Methods for the automatic appending (structure learn-
ing) of actions and intentions is also an open question.
REFERENCES
Breazeal, C. (1999). Robots in Society: Friend or Appli-
ance? In Agents99 Workshop on Emotion-based Agent
Architecture, pages 18–26, Seattle, WA.
Driver, E. and Morrell, D. (1995). Implementation of Con-
tinuous Bayesian Networks Using Sums of Weighted
Gaussians. In Besnard and Hanks, editors, Proceed-
ings of the 11
th
Conference on Uncertainty in Artifi-
cial Intelligence, pages 134–140, Montreal, Quebec,
Canada.
Horvitz, E., Breese, J., Heckerman, D., Hovel, D., and
Rommelse, K. (1998). The Lumi
`
ere Project: Bayesian
User Modelling for Inferring the Goals and Needs of
Software Users. In Proceedings of the Fourteenth
Conference on Uncertainty in Artificial Intelligence,
pages 256–265. AUAI, Morgan Kaufman.
Korb, K. and Nicholson, A. E. (2003). Bayesian Artificial
Intelligence. Chapman & Hall/CRC.
Lauritzen, S. L. (1992). Propagation of Probabilities, Means
and Variances in Mixed Graphical Association Mod-
els. Journal of the American Statistical Association,
87(420):1098–1108.
Murphy, K. P. (2002). Dynamic Bayesian Networks.
http://www.ai.mit.edu/∼murphyk. To appear in Prob-
abilistic Graphical Models (M. Jordan ed.).
Pearl, J. (1988). Probabilistic Reasoning in Intelligent Sys-
tems: Networks of Plausible Inference. Morgan Kauf-
mann.
Poland, W. and Shachter, R. (1993). Mixtures of Gaus-
sians and Minimum Relative Entropy Techniques for
Modeling Continuous Uncertainties. In Proceedings
of the 9
th
Annual Conference on Uncertainty in Arti-
ficial Intelligence (UAI-93), San Francisco, CA. Mor-
gan Kaufmann Publishers.
Rabiner, L. (1989). A Tutorial on Hidden Markov Models
and Selected Applications in Speech Recognition. In
Proceedings of the IEEE, volume 77, pages 257–286.
Roweis, S. and Ghahramani, Z. (1999). A Unifying Re-
view of Linear Gaussian Models. Neural Computing,
11:305–345.
Schrempf, O. C. and Hanebeck, U. D. (2004). A New
Approach for Hybrid Bayesian Networks Using Full
Densities. In Proceedings of 6
th
Workshop on Com-
puter Science and Information Technologies, CSIT
2004, Budapest, Hungary.
Schrempf, O. C. and Hanebeck, U. D. (2005). Evaluation
of Hybrid Bayesian Networks using Analytical Den-
sity Representations. In Proceedings of the 16
th
IFAC
World Congress, IFAC 2005, Prague, Czech Republic.
ICINCO 2005 - ROBOTICS AND AUTOMATION
256
