SUNSPOT SERIES PREDICTION USING ADAPTIVE

IDENTIFICATION

Juan A. Gómez Pulido, Miguel A. Vega Rodríguez, José Mª Granado Criado, Juan M. Sánchez Pérez

Departament of Computer Sciences, University of Extremadura, Spain

Keywords: System Identification. Prediction. Solar series. Parallelism.

Abstract: In this paper a parallel and adaptive methodology for optimizing the time series prediction using System

Identification is shown. In order to validate this methodology, a set of time series based on the sun activity

measured during the 20th century have been used. The prediction precision for short and long term

improves with this technique when it is compared with the found results using System Identification with

classical values for the main parameters.

1 INTRODUCTION

The time series (TS) prediction is a very important

knowledge area because the evolution of many

processes is represented as a time series:

meteorological phenomena, chemical reactions,

financial indexes, etc. Although the behaviour of any

of these processes may be due to the influence of

several causes, in many cases the ignorance of these

forces to study the process considering only the time

series evolution that represent it. By this reason,

numerous methods of time series analysis and

mathematical modelling have been developed.

System Identification (SI) techniques

(Söderström, 1989) can be used to obtain the TS

model. The model precision depends on the assigned

values to certain parameters. In SI, a time series is

considered as a sampled signal y(k) with period T

that is modeled with an ARMAX (Ljung, 1999)

parametric polynomial description of na dimension.

Basically the identification consists in determining

the ARMAX model parameters from measured

samples. Then it is possible to compute the

estimated signal ye(k) and to compare it with the

real signal, calculating the error (y(k)-ye(k)).

The recursive estimation updates the model in

each time step k, thus modeling the system. The

more sampled data are processed, the more precision

for the model, because it has more information about

the system behaviour history. We consider SI

performed by the well-known Recursive Least

Squares (RLS) algorithm (Ljung, 1999). This

algorithm is mainly specified by the constant λ

(forgetting factor) and the observed samples {y(k)}.

There is not any fixed value for λ, even it is used a

value between 0.97 and 0.995 (Ljung, 1991). The

cost function F we use is defined as the value to

minimize in order to obtain the best precision (see

equation 1, where SN is the sample number).

F(λ) =

Equation 1: The considered cost function

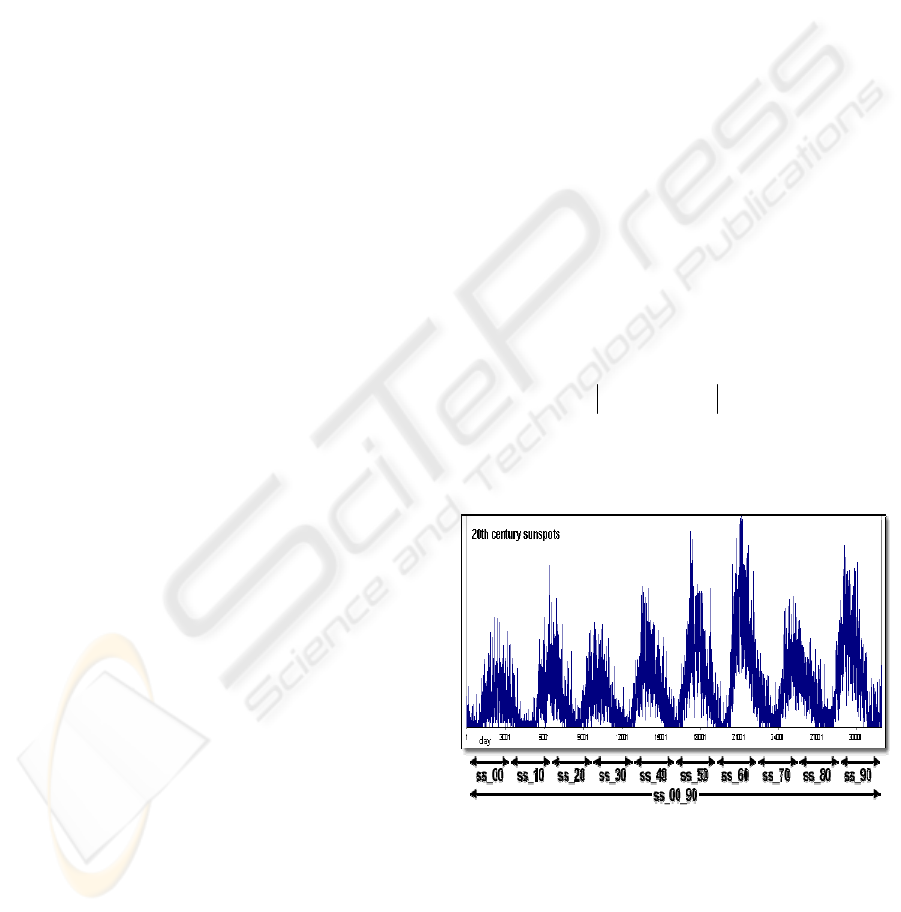
Figure 1: The sunspot time series used in this work

In this paper we use a time series set

corresponding to sunspot series obtained from

measured observations (ROB, 2004)(NOAA, 2004).

We have used 13 time series (Fig. 1) showing daily

sunspots: ten series (ss_00, ss_10, ss_20, ss_30,

ss_40, ss_50, ss_60, ss_70, ss_80 and ss_90)

corresponding to the sunspot measurements during

∑

− yy

−+=

)()(

SNkk

224

A. Gómez Pulido J., A. Vega Rodríguez M., M

Granado Criado J. and M. Sánchez Pérez J. (2005).

SUNSPOT SERIES PREDICTION USING ADAPTIVE IDENTIFICATION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 224-228

DOI: 10.5220/0001166202240228

 SciTePress

ten years each (for example, ss_20 compiles the

sunspots from 1/1/1920 to 31/12/1929), two series

(ss_00_40 and ss_50_90) covering 50 years each,

and finally one series (ss_00_90) that covers all

measurements of the 20th century.

2 SYSTEM IDENTIFICATION

BASED PREDICTION

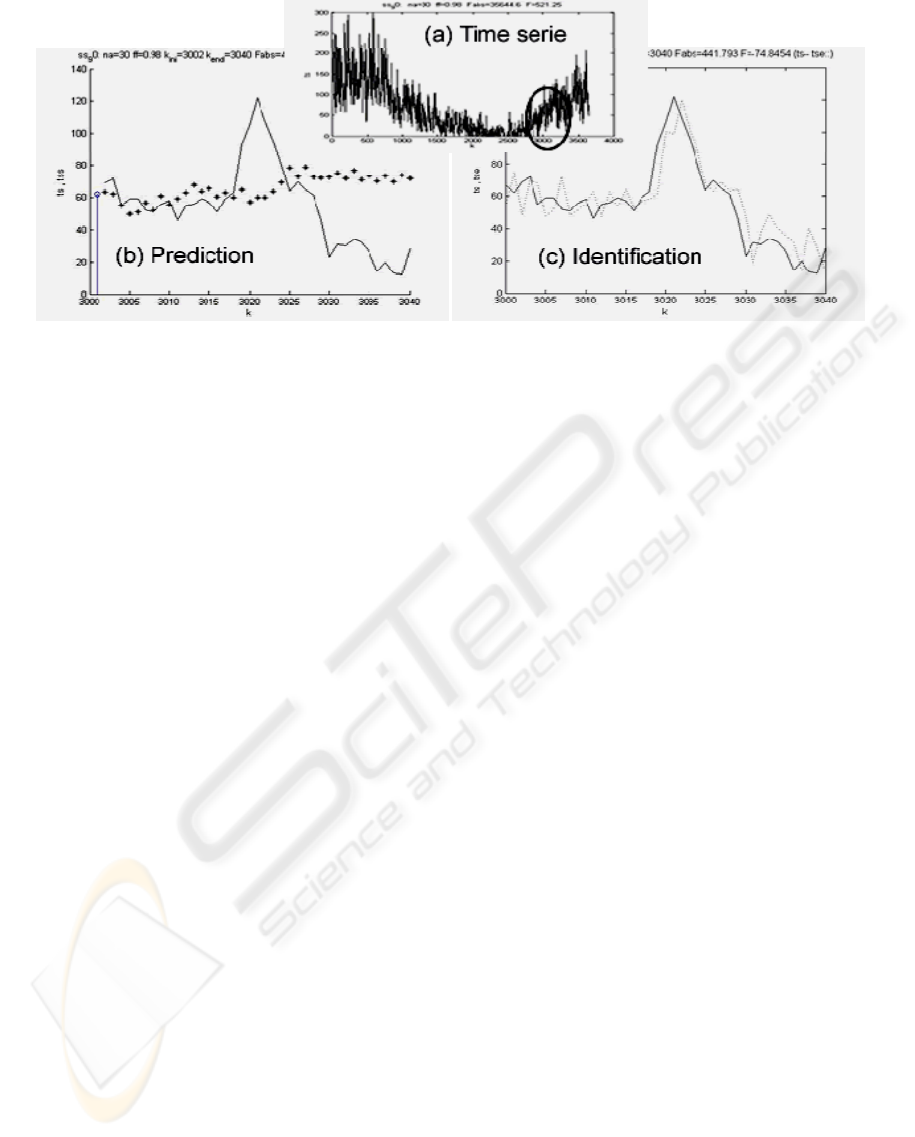
The recursive identification can be used to predict

the following behaviour of the time series (Fig. 2a)

from the data observed up to the moment. It is well

known that SI allows finding, in sample time, a

mathematical model of a system in the k time from

which is possible to predict the system behaviour in

k+1, k+2 and so on. As identification advances in

the time, the predictions improve using more precise

models. If ks is the time until the model is elaborated

and from which we carry out the prediction, we can

confirm that this prediction will have a larger error

while we will be more far away from ks (Fig. 2b).

The predicted value for ks+1 corresponds with the

last estimated value until ks. When we have more

data, the model starts to be re-elaborated for

computing the new estimated values (Fig. 2c).

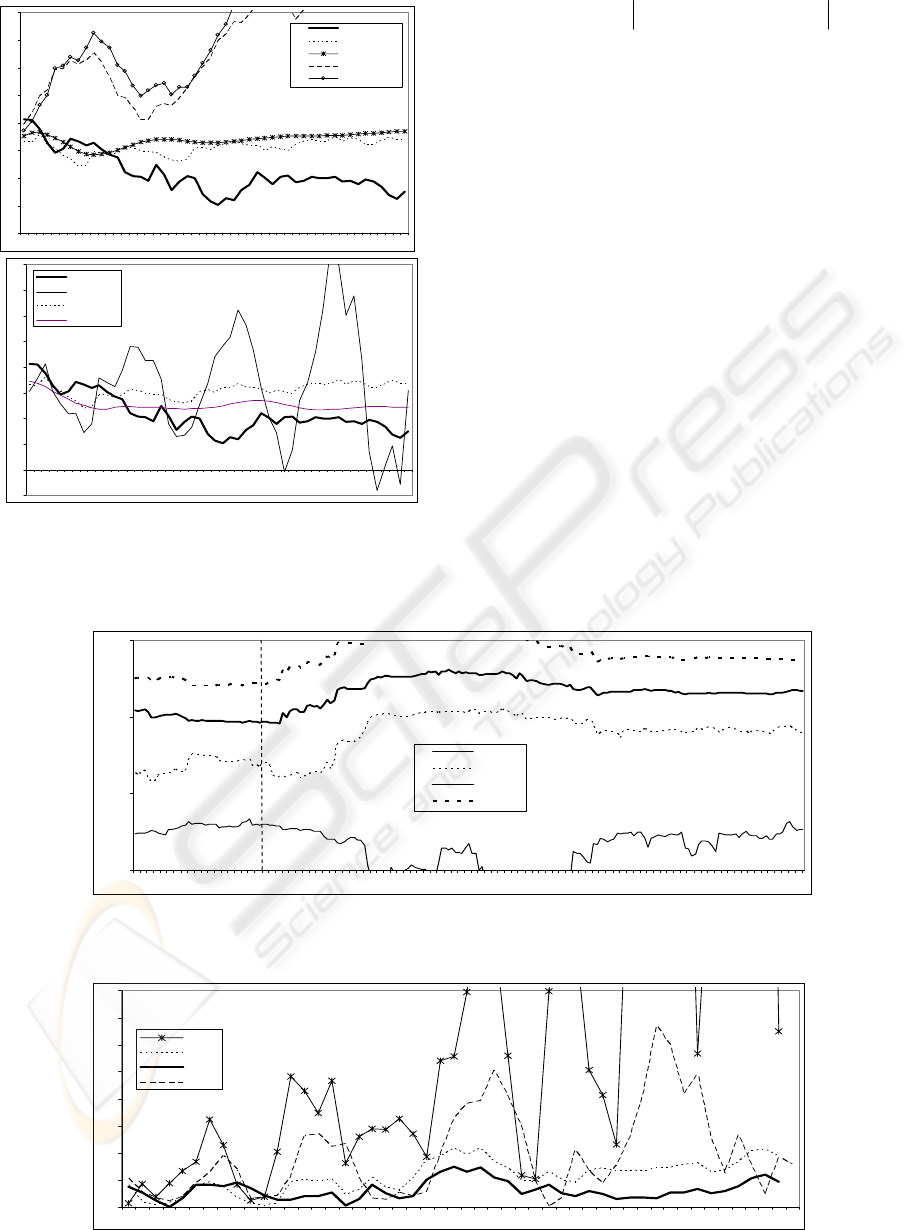
The main parameters of the identification are na y

λ. Both parameters have influence on the precision

of prediction results, as it shows Fig. 3. As we can

see, to establish an adequate value of na and λ may

be critical in order to obtain a good prediction. By

this reason, in the strategy of optimizing the

prediction, we try, first of all, to establish an

adequate dimension of the mathematical model for

finding the optimal λ value using an adaptive

algorithm.

In order to do that, many experiments have been

carried out. In these experiments, the absolute

difference between the real and predicted values has

been used in order to quantify the prediction

precision (see equation 2). So, in Fig. 4 the results of

many experiments are shown. In these experiments

different measures of the prediction error (for short

term DIFA1 and for long term DIFA50) for 200

different values of the model are obtained. In order

to establish reliable conclusions, these experiments

have been made for different ks values.

Figure 2: In (a) is displayed the ss_90 series. If ks=3000, we can see in (b) the long-term prediction based on the model

obtained up to ks (na=30 and λ=0.98). The prediction precision is reduced when we are far from ks. In (c) we can see the

predicted values for the successive ks+1 obtained from the updated models when the identification (and ks) advances

We use our own terminology for the prediction

error (DIFAX, where X is an integer) because like

this the reader can understand more easily the degree

of accuracy that we are measuring.

Provisionally we conclude that the increase of na

does not imply an improvement of the prediction

precision (however a considerable increase of the

computational cost is spent). This is easily verified

using large ks values (the elaborated models have

more information related to the time series) and

long-term predictions. From these results and as

trade-off between prediction and computational cost,

we have chosen na=40 to establishing it as the model

size for the future experiments

SUNSPOT SERIES PREDICTION USING ADAPTIVE IDENTIFICATION

225

DIFA(X) =

na influe nce (ff=0.98, ks=3600)

Figure 3: Influence of the model dimension na and

forgetting factor λ on the short-term (ks) and long-term

(ks+50) prediction for the ss_90 series

Eq.2. The cost function in the prediction

measurements.

The key parameter for the prediction optimization

is λ. Fig. 5 shows, with more detail than in Fig. 3b,

an example of the λ influence in the short-term and

long-term predictions by representing its precision

measure. It is clear that for any λ value is more

precise the short-term prediction than the long-term

prediction. However, we can observe the chosen

value for λ is critical for finding a good predictive

model (from the four chosen values, λ =1 produces a

better prediction, even in the long term). This

analysis has been confirmed making a great number

of experiments with the sunspot series, modifying

the initial prediction time, ks.

Figure 4: Measures of the prediction precision for the ss_90 time series from ks=3600, using λ=0.98. The measures have

been made for models of dimensions between 2 and 200

Figure 5: Influence of λ in the prediction precision for ss_90 with na=40 and ks=3600

100

ks+1 ks+8 ks+15 ks +22 ks +29 ks+36 ks +43 ks +50

tss (na=40)

tss (na=10)

tss (na=75)

tss (na=100)

FF influence (na =40, ks=3600)

-50

100

150

200

250

300

350

400

ks+1 ks+8 ks+15 ks+22 ks+29 ks+36 ks +43 ks+50

ts s (ff=0.95)

ts s (ff=0.98)

tss (ff=1)

100

1000

10000

2 13 24 35 46 57 68 79 90 101 112 123 134 145 156 167 178 189 200

log10

DIFA 1

DIFA 10

DIFA 25

DIFA 50

DIFA(X)

(na = 40, ks=3600)

100

150

200

250

300

350

400

1 8 15 22 29 36 43 50

ff=0.9

ff=0.98

ff=1.0

ff=0.95

∑

+−+

iksyiksy

)()(

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

226

3 OPTIMIZING THE

PREDICTION WITH AN

ADAPTIVE STRATEGY

In order to find the optimum value of λ, we propose

an adaptive algorithm inspired on the artificial

evolution (Goldberg, 1989)(Rechenberg, 1973) and

on the simulated annealing mechanism (Kirkpatrick,

1983). This algorithm, named PARLS (Parallel

Adaptive Recursive Least Squares), has been

implemented using parallel processing units, built

with neural networks (Gomez, 2003). In PARLS the

optimization parameter λ evolves to predict new

situations during the iterations of the algorithm. In

other words, λ evolves at the same time that

improves the cost function performance.

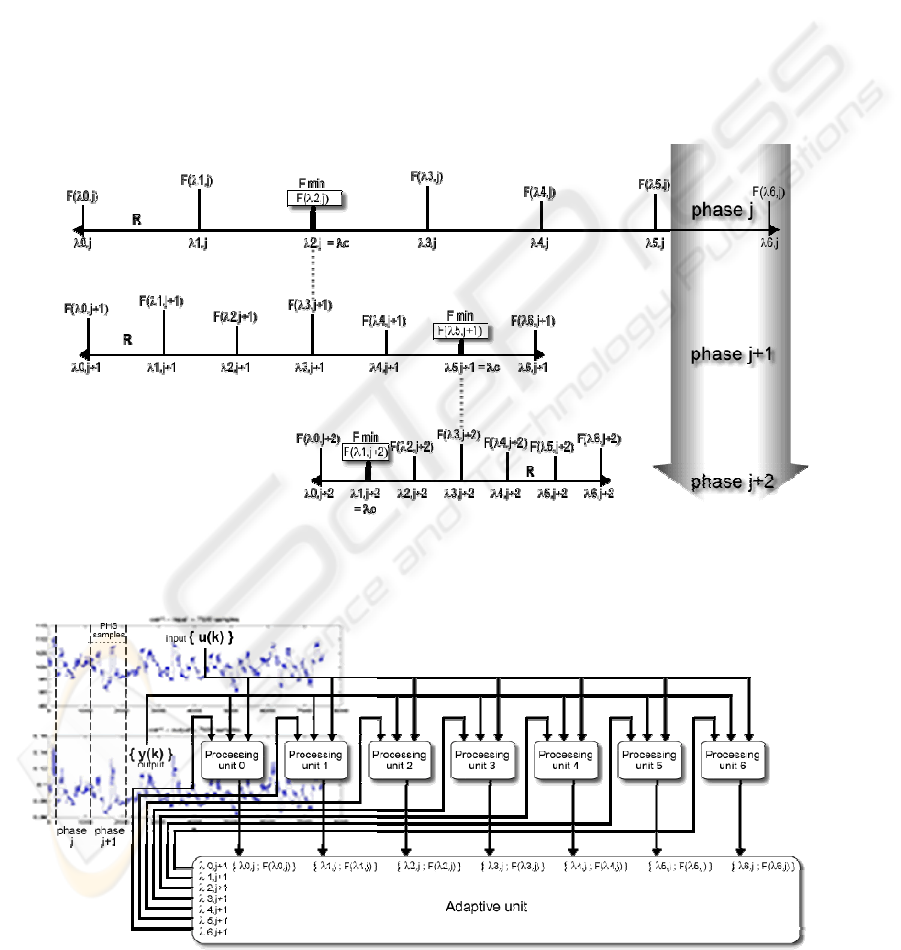
The evolution mechanism (Fig. 6) is as follows:

The first phase starts building a set of λ values

covering the interval R uniformly from its selected

middle λc. An equal number of parallel processing

units (PUN) perform RLS identification with each λ

in the interval, for a given number of sampling times

(PHS). Then, the optimum λ is that whose

corresponding cost function F is the minimum of all

computed F, and from it a new set of λ values is

generated and used in the next phase to perform new

identifications during the following PHS samples. F

is defined as the accumulated error of the samples in

each phase, and the generation of new λ values is

made with a more reduced R by the factor RED.

Finally, PARLS stops when the number of phases

(PHN) is reached, according to the total number of

samples (TSN).

Figure 6: All the λ values in the same phase running in the processing units are generated in the R interval from the

previous phase optimum λ found, corresponding with the smallest F

Figure 7: PARLS architecture. A set of processing units generates the next set of λ values to be computed by RLS algorithm

SUNSPOT SERIES PREDICTION USING ADAPTIVE IDENTIFICATION

227

Therefore, PARLS could be considered as a

population-based rather than a parallel

metaheuristic, because each processing unit is able

to operate isolated, as well as the tackled problem

itself as only a single real-valued parameter (λ) that

is optimized.

In Fig. 7 we can see a top-level view of the

PARLS architecture: a set of processing units that

performs system identification in each phase sends

the errors found to the adaptive unit. This unit will

generate the new search range in a feedback loop.

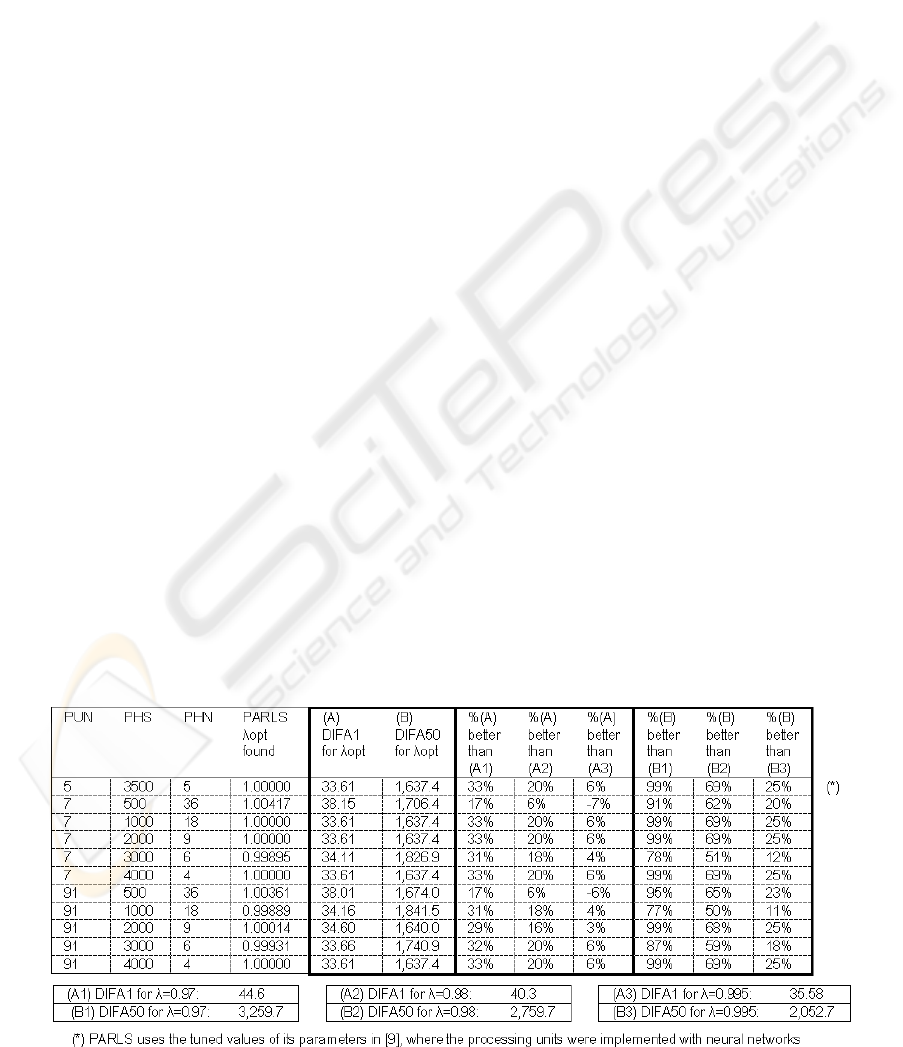
4 EXPERIMENTAL RESULTS

Some results found using the PARLS algorithm for

predicting the next values from the last value

registered for the time series of the sun activity

indexes of the 20th century second half are shown in

Table 1. The prediction precision is given by the

results DIFA1 (short term) and DIFA50 (long term).

These results are compared, for evauating purposes,

with the obtained using RLS identification with

some values of λ inside the classical range (Ljung,

1991). We can see how PARLS finds a better

precision.

5 CONCLUSIONS

The results shown in Table 1 are a part of the great

number of experiments carried out using different

time series and initial prediction times. In the great

majority of the cases, PARLS offers better results

than if λ random values are used. However, we are

trying to increase the prediction precision. Thus, our

future working lines suggest using genetic

algorithms or strategies of analogous nature for, on

the one hand, finding the optimum set of values for

the parameters of PARLS and, on the other hand,

finding the optimum couple of values {na, λ}.

ACKNOWLEDGEMENTS

This work has been developed thanks to TRACER

project, TIC2002-04498-C05-01.

REFERENCES

Söderström, T. et al., 1989. System Identification.

Prentice-Hall, London.

Ljung, L., 1999. System Identification – Theory for the

User. Prentice-Hall, London.

Ljung, L., 1991. System Identification Toolbox. The Math

Works Inc, NY.

ROB, Royal Observatory of Belgium, Brussels, 2004.

Sunspot Data Series. http: // sidc.oma.be / html /

sunspot.html

NOAA, National Geophysical Data Center, 2004. Sunspot

numbers. http: // www. ngdc. noaa.gov / stp / SOLAR /

ftpsunspotnumber.html

Goldberg, D.E., 1989. Genetic Algorithms in Search,

Optimization and Machine Learning. Addison Wesley.

Rechenberg, I., 1973. Evolutionsstrategie: Optimierung

technischer systeme nach prinzipien der biolgischen

evolution. Formmann-Holzboog Verlag.

Kirkpatrick, S., Gelatt, C., Vecchi, M., 1983. Optimization

by Simulated Annealing. In: Science, 220, 4598, 671-

680.

Gómez, J., Sánchez, J., Vega, M., 2003. Using Neural

Networks in a Parallel Adaptive Algorithm for the

System Identification Optimization. In: Lecture Notes

on Computer Sciences, vol. 2687, 465-472. Springer-

Verlag.

Table 1: A sample of the prediction precision results for short and long term, compared with the ones obtained from

three classical values of λ: 0.97, 0.98 and 0.995. The settings for this experiment are: benchmark= ss_50_90; na=40;

ks=18,210; TSN=18,262; λc=1; R=0.2; RED=2

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

228