
A SMOOTHING STRATEGY FOR PRM PATHS
Application to 6-axes MOTOMAN manipulator
Reda Guernane, Mahmoud Belhocine
Divison Robotique et Productique , Centre de Développement des Technologies Avancées,CDTA, Cité 20 août 1956,
B
P 1
7,
Haouch Oukil, Baba Hassen,Alger, Algeria
Keywords: Probabilistic Roadmap, A*, smoothing, motion planning, 6-axis manipulator, collision checks.
Abstract: This paper describes the use of the probabilistic motion planning technique SBL “Single-Query
Bidirectional Probabilistic Algorithm with Lazy Collision Checking” or in motion planning for robot
manipulators. We present a novel strategy to remedy the PRM “Probabilistic Roadmap” paths which are
both excessively long and velocity discontinuous. The optimization of the path will be done first through
Coarse optimal lazy A* optimization and then through a Fine cutting-triangles-edge one, the edges
discontinuities are smoothed with cubic polynomials taking the robot’s specific Dynamic and Cinematic
constraints. The whole strategy is applied to the 6 axes robot Manipulator MOTOMAN SV3X.
1 INTRODUCTION
The motion planning problem has been in a great
difficulty solving path planning for real industrial
robot manipulator which are usually 6 or above
degrees of freedoms (dofs). The traditional
techniques (Latombe, 1991) can hardly solve
problems until 4 or 5 dofs, while its known to be
definitely impossible for 6 dofs in 3D space.
The introduction of random techniques in
roadmap generation (Kavraki, 1996) has greatly
simplified the planning problem, theirs greatest
advantages being, easiness of understanding,
implementing, they can deals with complicated
scene and can solve problem with high number of
dofs.
Their idea consists of randomly sampling the
configuration space (Lozano-Péréz, 1979) of the
robot in order to capture the connectivity of free
space, static configurations are tested using fast
hierarchical collision checking algorithms (Larsen,
1998), the configurations are then connected with a
simple but very fast local planner to obtain the so
called Roadmap. Roadmap techniques are generally
classified in two branches, the Multiple Query and
the Single Query, for the first one a roadmap is pre-
calculated and used later for multiple queries, the
second one does not precompute such roadmap but it
explores the free space starting from given initial
configuration in search for a final one, the
constructed graph is valid only for one query. but
PRM generated paths are know to be discontinuous
and far from optimal.
Among all PRM variants, we have chosen the
SBL (Sanchez-Ante, 2001) because it is the most
successful one due to its speed and behaviour even
in cluttered environment. Still, the path generated is
far from optimal due to the fact that the algorithm
generates nodes randomly and diffuses them
homogeneously in the free space, which is not
necessarily the shortest path. The SBL is called:
-Single query: the network is recalculated for
each start/goal pair.
-Bidirectional: because the network construction
is started simultaneously from the start and goal
configuration.
-Lazy collision: because the collision checks are
delayed until they are extremely needed (Bohlin,
2000).
Our work consists at optimizing the Raw PRM
path in some sense by modifying the PRM path; this
path is the optimal among those using only the nodes
on the raw path and connected with straight line in
C-space. Then using a fine optimization scheme we
optimize further the path from the previous step,
finally we smooth the sharp corners with cubic
polynomial taking the robot specific dynamic and
kinematic constraints. The result is an optimized
smooth trajectory ready for execution.
205
Guernane R. and Belhocine M. (2005).
A SMOOTHING STRATEGY FOR PRM PATHS - Application to 6-axes MOTOMAN manipulator.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 205-210
DOI: 10.5220/0001167202050210
Copyright
c
SciTePress

2 REALTED WORKS
The use of smoothing on paths was already
suggested in 2D workspaces but less in 3D
workspaces. In (Quinlan, 1993) the authors represent
the path as an elastic band under tension forces to
pull the path tight. Repulsion forces from the
obstacles are added to keep the path from “hugging”
the obstacles. B-splines are used in (Foley, 1990)
(Kant, 1987) to construct smooth paths from a cell
decomposition of the free space. Cubic splines are
also used in (Tondu, 1999). The use of smoothing
techniques on PRM paths has been already
proposed, the authors often use shortcutting segment
or parts of segment methods already used in
(Laumond, 1990) (Berchtold, 1994). In most of the
cases after such smoothing, paths are shorter but still
not optimal in any sense and discontinuous in
velocity.
3 COARSE OPTIMIZATION
Given a graph of nodes relating the initial and final
nodes, many search technique are available to obtain
the path composed of a sequence of nodes relating
the start and goal nodes.
The A* algorithm obtains the optimal path out of
the graph of nodes without the need to explore the
whole graph, this is done is by guiding the search
with a cost function describing heuristic rules.
The evaluation function
f
ˆ
is defined such that
its value
()
nf
ˆ
at any node n is an estimate of the
minimum cost path constrained to go through n. This
is calculated using an estimate of the cost of the
minimal path from the start node to node n plus an
estimate of the cost of the minimal path from node n
to the goal node.
()
nf
ˆ
=
g
ˆ
(n) +
h
ˆ
(n)
It is straightforward to calculate a value for
g
ˆ
by summing the arc costs of the path already found
from the start node to node n. Finding a value for
h
ˆ
is not so simple and heuristic information obtained
from the graph has to be relied upon. For example,
the straight line distance from node n to ng can be
used as the value for
h
ˆ
. If
h
ˆ
is an underestimate of
h then A* is guaranteed to find the minimum cost
path and the algorithm is said to be admissible. A
proof is given in (Doyle, 1995).
In the usual A* and graph searching algorithms
require a graph containing all admissible edges or
segment between nodes, whereas we have only
edges between consecutive nodes of the PRM path
so we will need to construct a graph out of the path
nodes by testing the straight line segments between
each pair, this may be costly especially in
complicated scene where the number of triangles is
extremely high. In order to avoid collision testing all
edges, we propose to “lazify” the A* algorithm.
3.1 Postponing Collision Checks
The idea is delay segment collision testing until it is
“necessary”, the necessity in our case is when a node
is sorted to be placed in the optimal path.
In the beginning all pair of nodes are assumed to
have and admissible edge joining them except for
the (n
s
,n
g
) as we know it is not admissible (this
trivial solution should have seen tested before the
launching the planner)
Initially a node can be expanded to all other
nodes in the graph, except for the initial node that
cannot be expanded to the goal node.
In traditional A* the use pointers to specify
relation between nodes resulting from a certain node
expansion, here we use a parent-child notion, each
node expand as a father of the resulting child node.
Also, each of the raw PRM path nodes can be
expanded to all other nodes with two exceptions:
- The starting node does not expand to the goal
one.
- The goal node does not expand to any node.
Lazy A* algorithm
1. insert start node n
s
in a list called OPEN
2. While
3. n ← SORT
4. if TEST(n) is true then
4.1. if n is the goal node then terminate the
algorithm & use pointers to extract optimal
path else EXPAND(n).
else REALOCATE(n)
5. end while loop
The OPEN that will hold all nodes to be
expanded; nodes are added and removed in each
iteration. The While loop is an indefinite loop,
whereas standard A* the condition is the OPEN list
not empty, this was so because we are sure that the
algorithm will find a solution before OPEN is
empty, the loop is terminated once the solution is
found
3.2 List Sorting
The SORT procedure will return the node with
minimum cost path constrained to go through this
later in the OPEN list, this also means that we do not
ICINCO 2005 - ROBOTICS AND AUTOMATION
206
sort all the OPEN list in any given order., the
minimum cost node n is also removed from OPEN.
3.3 Testing segments
Algorithm for TEST
1. let n
p
the parent of node n
2. if edge E(n
p
, n) belong to PRM path return
true
3. if CLEAR(E(n,n
p
)) return true
4. return false
The TEST(n) is an algorithm that will test if the
segment relating the current node n to its father node
(the one which has
ENGENDERED n in OPEN) is clear
or notIf the segment joining node n and its parent
node belongs to the raw path generated by RPM
planner then the segment is declared safe (there is no
need to test the segment since it is have been tested
during PRM planning,), otherwise the segment is
tested for collision.
3.4 Reallocating a node
If the segment relating node n to its parent node
happens to be colliding, then reallocated will try to
add n as a child to another node already in CLOSED
list. Among all nodes in CLOSED that have not
already been tested with n, n will be added to the
one with minimum cost path constrained to go n.
If there are no such node in CLOSED then n will
remain "orphan" and out of the OPEN list until it is
inserted back by some node.
Algorithm for REALLOCATE
1. for all nodes in CLOSED that have not been
already tested with n
1.1. choose node n
p
with minimum cost path
constrained to go through n
1.2. set n
p
as the father of node n
2. if a node n
p
was found then insert node n in
OPEN
3.5 Node Expansion
The EXPAND procedure is responsible for inserting
a node’s children to OPEN taking care the following
conditions:
- If a child is already in CLOSED or in OPEN
it will not be added to neither of the lists.
- If a child node is already in OPEN and its
current cost path is higher than the cost of
going through the current parent node n, this
later is set as its new parent with the cost
updated to the new one.
The cost function is usually the distance from
initial and final configurations criterion, the cost of
the path through a stain number of nodes is the sum
of the costs of individual segments or edges costs.
We could choose the Euclidian norm of the edge, or
more generally a weighted Euclidian norm
4 FINE OPTIMIZATION
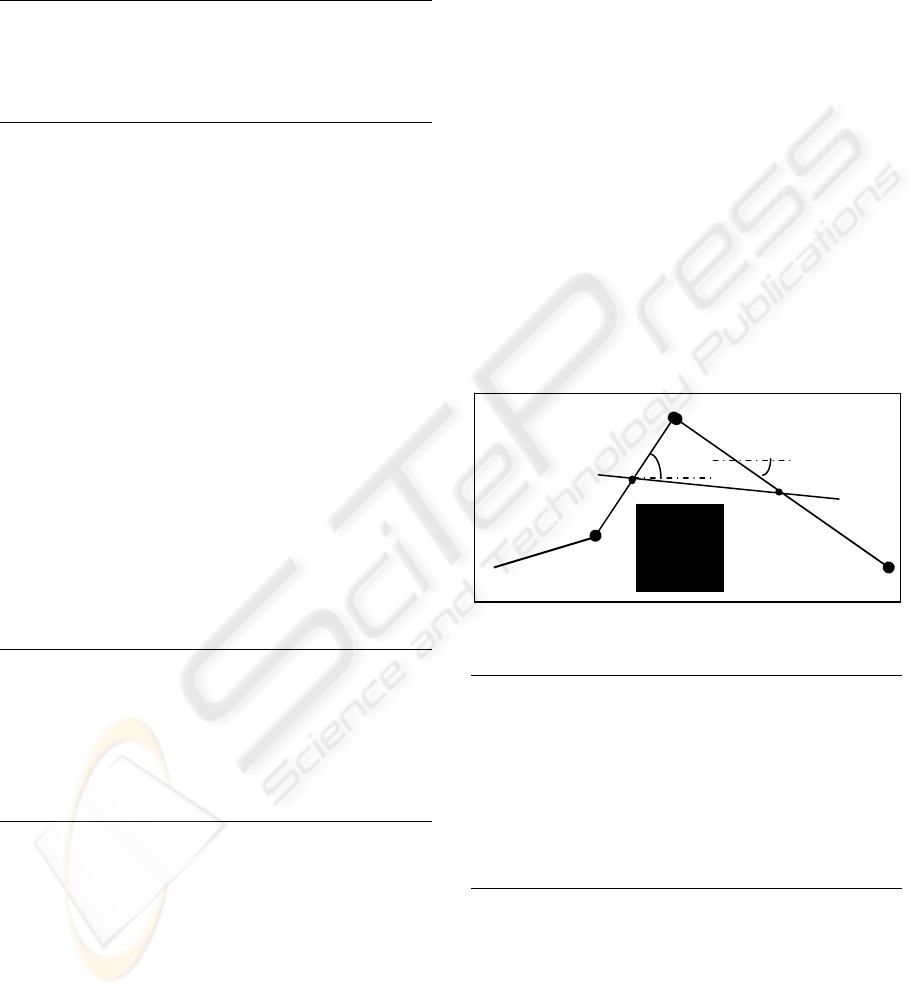
Here we use a simple cut-triangle-edge scheme,
many variant are found in (Berchtold, 1994); for
each two consecutive segments E(n
1
,n
2
) , E(n
2
,n
3
) ,
we try to cut the triangle edge represented by n
1
n
2
n
3
(figure 1 ) with a segment E(n’,n”) where n’, n” are
at the middle of segment E(n
1
,n
2
) , E(n
2
,n
3
)
respectively .This techniques will have two
advantage:
1- Smooth the path by replacing the sharp
angles with wider ones.
2- Optimize the path in any norm (triangle’s
inequality
Cutting-tiangle-edge Algorithm
1. Input path T
2. For each segment E(n
i
, n
i+1
) of path T ,i=1, m-1
2.1. Calculate node n
i
' at the middle of segment
E(n
i
, n
i+1
)
3. For each segment E(n
i
',n'
i+1
) , i=1, m-2
3.1. If segment E(n
i
',n'
i+1
) is Clear
3.1.1. replace segments E(n'
i
, n
i+1
) and
E(n
i+1
, n'
i+1
) in T with E(n
i
',n'
i+1
)
4. Return T
5 CUBIC SMOOTHING
Since the PRM path are inherently peace-wise
curves. The transition from one line segment to the
next induces an abrupt change in direction. The
robot cannot execute the corresponding trajectory
without coming at rest at each of these points. In
Figure 1: cutting-triangle-edge technique
A SMOOTHING STRATEGY FOR PRM PATHS: Application to 6-axes MOTOMAN manipulator
207

order to avoid this, we should have a continuous
joint velocity. So we have to smooth path , we will
accomplish this taking care to modify the least
possible the original one, to achieve this , we smooth
the corners using a polynomial with a given degree
and parameters.
First and second order polynomial are easy to
calculate but they fit poorly, fourth order and higher
polynomials provides seamless fit but they are very
difficult if not impossible to calculate, that is why
we believe the compromise would be to choose the
cubic polynomial (Brock, 1999). The parameters are
not complicated to calculate, the curve has C
2
continuity and it enables tighter approximation to the
turn compared to quadratic polynomial. We will
here explain the procedure for a single joint; the
same applies to all remaining joints. The joint
position turn is governed by the following cubic
polynomial:
3
3
2
210
)( tatataatq +++=
(1)
The duration d of the cubic turn (Figure 2) is thus :
max
2
q
q
d
∆
=
(2)
Figure 2: cubic smoothing.
∆ q
is the change in velocity of the two
consecutive segments. The detailed description of
the calculation of the start and the end
configurations of the cubic turn and the cubic
parameters are found in (Brock, 1999). The Cubic
turns are tested for collision by sampling the
polynomial to a number of configuration m linearly
separated by a distance ε sufficiently small, if all m
configurations are collision free than the cubic turn
is collision free.
6 SIMULATION RESULTS
SBL planner, smoothing techniques are written in
C++, the animation and visualization API was also
implemented in C++ using COIN visualization
library and its binding SoQt.
The tests were run on a 1.7GHZ Pentium 4 PC
with 128 Mbytes of main memory running Linux
OS. We have constructed a 3D CAD model for the 6
axes MOTMAN SV3X manipulator.For the PRM
planner, the maximum number of milestones
allowed to be generated is 10000 and the distance
threshold ρ for the segment discretization was set to
0.015. We have simulated a robot Gross movement
from initial configuration to a final configuration in
the scene shown in figure 3a, 3b respectively.
Running the SBL planner for the given query gives
the results shown in table 1.
Table 1: result of SBL planner query for the given
example.
Here the generated raw path is a 7 node path,
figure 4a shows path traced by a point on the end
effector along the SBL path. It is apparent that the
path is lengthy and requires optimization.
6.1 Lazy A* application
Using a simple Euclidian path cost, the path is
shown on figure 4b with a cost of 6.66959.
If we place a weight of 10 on the shoulder axis
weighted Euclidian norm, while we put a weight on
only one, this lead to more Minimization of
Euclidian distance along that axis,. The path is
shown in figure 5a and its cost being 9.58155.
Total
-time
(s)
#nods
In trees
#nodes
In path
#total
CC
#CC
in path
#
sampled
nodes
total C
C
time(s)
0.39
55 9 448 123 136 0.38
d
i
q
starting
q
e
ndi
ng
t
(s)
q
(a) (b)
Figure 4: (a) raw trajectory, (b) Euclidian norm A* path.
(a) (b)
Figure 3: configurations, (a) initial, (b) final .
ICINCO 2005 - ROBOTICS AND AUTOMATION
208

L
∝
norm minimization: In this example we
penalize the maximum joint movement of the edge
between two nodes; the generated path is shown in
figure 5b with a cost of 5.7734.
a) b)
Figure 5: a) lazy A* with shoulder axis penalty path;
b) L
∝
minimization lazy A* path.
6.2 Lazy A* versus A*
In order to evaluate the efficiency of the lazy A*
with the standard A* we have run the SBL planner
for 10 times for the same query, hence 10 different
path have been generated. We have calculated the
number of collision checks required for each
technique in order to find the optimized path in some
sense. The results are:
- average Collision checks for Lazy A*: 107.7
- average Collision checks for A*: 823.4
The ratio of the two averages is ≈1/8
- Lazy A* time is = 0.25 s
- A* time is = 0.95
Using scenes that are extremely complicated will
favour more and more the use of the lazy A*
algorithm.
6.3 Lazy A* versus random
shortcutting
Random shortcutting (Laumond, 1990) segments
techniques are frequently used to reduce the number
of segments on the path, but the resulting path is not
necessarily optimal in any sense.
Figures 5a and 5b show the result of the
application of the Lazy A* and the Shortcutting
method respectively, in the chosen Euclidian norm,
only the A* managed to find the Optimal path, the
cost function being 6.3212, the cost for the
Shortcutting method is 7.7305.
a) b)
Figure 6: a) shortcutting path. b) Lazy A* path.
6.4 Cutting-triangle-edge
application
We apply this technique on the optimal A* path
(figure 4b), it is clear that the application of this
technique will not dwarf any optimization gained
from the A* because it only shortcut parts of
segments which is more optimized in any norm used
(this is the triangle’ inequality which is a condition
of normality).
The results are:
- the algorithm managed to cut all segment
- the cost of path generated is : 5.77343
- the time taken is : 0.05 seconds
Figure 7a shows the generated path.
a) b)
Figure 7: a) cutting-triangle-edge path: b) cubic smoothing
path.
6.5 Cubic smoothing and trajectory
generation
Up to now, we where dealing with C-space spatial
paths, in order to execute the path parameterized
with time or simply the trajectory, we need to
associate joint velocities with each segment of the
path. It is clear that if we require the robot to follow
a C-space straight line segment of the path, then we
should synchronize all joints with constant velocities
so that the joint movement is linear.
What we have done is chose a velocity v that is
smaller or equal than any of the physical maximum
joint velocities. v is fixed for all segments making
C
1
C
2
C
2
A SMOOTHING STRATEGY FOR PRM PATHS: Application to 6-axes MOTOMAN manipulator
209

the path. Using v and the maximum joint
displacement in the given segment, we calculate the
segment duration d
i
, d
i
is used to calculate the joint
velocities for the remaining 5 joints. In this way, we
guarantee our piece-wise path following and prevent
assigning later joint velocities that exceed actual
ones.
Choosing v to be 0.10s
-1
, we calculated the 6
joints velocities and durations for all 4 segments
making the path issued from the fine optimization
step (figure 7a).
The total duration of the trajectory is 9.6246
seconds. Using this trajectory along with typical
maximum normalized acceleration of 0.20s
-2
we
calculated the 3 cubic durations and polynomial’s
parameters. Table 2 shows the calculated cubic
durations for the three corners smoothed.
Figure 7b shows the path with smoothed corners.
Table 2: cubic smoothing durations
q
1
q
2
q
3
q
4
q
5
q
6
c
1
d(s)
0.1851
0.3350
0.1122
0.0125
0.1466
0
c
2
d(s)
0.2867
1.3977
0.1125
0.0462
0.1749
1.0765
c
3
d(s)
0.4878
0.1580
0.4982
0.1064
0.5288
0.9235
The cubic duration that is null means no cubic
turn is needed due to the velocities of the two
consecutive segments being equal. It is clear that the
total trajectory duration can be reduced by using
higher joint velocities, but the cubic deviation will
be consequently higher.
7 CONCLUSION AND FUTURE
WORKS
The results show that the PRM paths can be
optimized through any criterion thought the Lazy A*
algorithm instead of blind shortcutting techniques,
the proposed lazy A* calculate the optimal path with
minimum collision checks compared to standard A*,
the remaining edges are smoothed thought cubic
polynomial resulting in minimum deviation from
original path, the final trajectory is an optimized
smooth trajectory ready for execution.
We are implementing the approach on the
physical MOTOMAN SV3X 6-axes manipulator,
and also working on a scheme to optimize
furthermore the PRM path by using an enhanced A*
algorithm along with other techniques.
REFERENCES
Latombe J-C., 1991. Robot Motion Planning, Kluwer
Academic Publishers.
Kavraki, E., Svestka, P., Latombe, J-C. and Overmars,
M.H, 1996. Probabilistic Roadmap for path planning in
high-dimensional configuration spaces, IEEE Trans,
Robot & Autom, 12(4) 556-580.
Lozano-Péerez, T. and Wesley, M.A, 1979. An Algorithm
for Planning Collision Free Paths among Polyhedral
Obstacles, Communications of the ACM, vol. 22 ,no.
10, pp. 560-570.
Larsen, E., Gottschalk, S., Lin, M-C., Manocha, D., 1998.
Fast Proximity Queries with Swept Sphere Volume»,
Technical report TR99-018, Department of Computer
Science, University of N. Carolina, Chapel Hill.
Sanchez-Ante, G. and Latombe, J-C., 2001. A single-
query bi-directional probabilistic roadmap planner with
lazy collision checking, In Proc, 10th Int. Symp. Of
Robotics Research, ISRR’2001, Lorne, Victoria,
Australia.
Bohlin, R. and Kavraki, L., 2000. Path Planning Using
Lazy PRM. In Proceedings of the IEEE International
Conference on Robotics and Automation, pp. 521–528,
IEEE Press, San Fransisco, CA.
Quinlan, S. and Khatib, O., 1993. Elastic Bands:
Connecting Path Planning and Control,’’ Proceedings
of the International Conference on Robotics and
Automation, Atlanta, GA, pp. 802-807.
Foley, J., van Dam, A., Feiner, S. and Hughes,. J. 1990
Computer Graphics: Principles and Practices, 2nd ed.
Addison-Wesley.
Kant, K. and Zucker. S-W. 1987. Planning smooth
collision-free trajectories: path, velocity, and splines in
free-space,” The International Journal of Robotics
Research, 2(3), pp.117–126.
Tondu, B. and Bazaz, S.A. 1999. The Three-Cubic
Method: An Optimal Online Robot Joint Trajectory
Generator under Velocity, Acceleration, and
Wandering Constraints,” The International Journal of
Robotics Research, vol.18, n°9 pp.893–901.
Laumond, J-P. Taix, M. and Jacobs, P. 1990. A motion
planner for car-like robots based on a global/local
approach," Proc. IEEE Internat. Workshop Intell.
Robot Syst. 765-773.
Berchtold, S. and Glavina, B., 1994. A scalable optimizer
for automatically generated manipulator motions, Proc.
IEEE/RSJ/GI Int. Conf. Intelligent Robots and
Systems, 1796-1802, München, Germany.
Doyle, A-B., 1995. Algorithms and Computational
Techniques for Robot Path Planning”, Phd thesis.
Brock, O., 1999. Generating robot motion; the integration
of planning and execution, PhD thesis, Stanford
University.
ICINCO 2005 - ROBOTICS AND AUTOMATION
210
