ANN-BASED MULTIPLE DIMENSION PREDICTOR FOR

SHIP ROUTE PREDICTION

Tianhao Tang, Tianzhen Wang

Institute of Electrical & Control Engineering,Shanghai Maritime University, 1550 Pudong Road,Shanghai,China

Keywords: Nonlinear time series model, adaptive predictor, artificial neural networks, data mining.

Abstract: This paper presents a new multiple dimension predictive model based on the diagonal recurrent neural

networks (PDRNN) with a combined learning algorithm. This method can be used to predict not only

values, but also some points in the multi-dimension space. And also its applications in data mining will be

discussed in the paper. Some analysis results show the significant improvement to ship route prediction

using the PDRNN model in database of geographic information system (GIS).

1 INTRODUCTION

The problem of prediction is denoted to estimate the

output of future according to input and output of

now and past in some system. Since Kolmogorov

presented a linear optimal predictor in 1941,

different kinds of trend analysis methods and

prediction models have been used for forecasting

and control. In this field, the time series prediction

model (Box and Jenkins, 1970) and the self-tuning

predictor (Wittenmark, 1974) were two kinds of

classical prediction methods. The tradition

prediction theories based on time series were

developed from linear auto recurrent moving

average (ARMA) models. And then these theories

were extended to nonlinear process. But, if using the

tradition predictive theories, it needs to solve the

problems: system modelling, parameter estimating,

model modifying and trend forecasting on-line.

In order to solve these problems, some

intelligent prediction methods were discussed, in

which the forward neural networks with BP

algorithm were used more popularly. Prediction

based on ANN has made an overwhelming impact

on many disciplines. But there are some difficulties

in prediction, particularly in the prediction of multi-

variable and non-steady dynamic process.

Recent years, scholars had done much research,

and made some progresses in this filed. We have

researched predictive models using neural networks,

such as an ANN-based nonlinear time series model

for fault detection and prediction in marine system

(Tang, 1998) and an adaptive predictor based on a

recurrent neural network for fault prediction and

incipient diagnosis (Tang, 2000). Furthermore a

direct multi-step adaptive predictor based on a

diagonal recurrent neuron network was presented for

intelligent system monitoring (Dou, 2001). These

models increased the precision and self-adaptation

of prediction in a manner.

However, there existed a problem: former

prediction methods based on time series models

could only approach or predict processes with one

kind of attribute, such as temperature, pressure and

flow in an industry process, or stock values and

GDP in the economic process. In this case, every

parameter must be separately denoted if using a

traditional time series model in the dynamic process.

But some objects have more than two kinds of

attributes, and must be represented as one predictive

model. For example, a ship route has two kinds of

attributes: longitude and latitude. A satellite position

has three kinds of attributes: longitude, latitude and

altitude. So the question of how to predict objects

with several attributes is an important problem in

practice.

This paper discusses self-adaptation prediction

methods based on ANN, and presents a multi-

dimension predictive model based on parallel

diagonal recurrent neuron network (PDRNN) with

TD-DBP combined algorithms for time series multi-

step forecasting. The paper takes a step forward to

use this model in data mining of GIS. Some

simulation resolves show the model is able to predict

a ship’s route according to its position from GPS.

2 PRINCIPLE OF ANN-BASED

PREDICTOR

The basic issue of a predictor can be described as:

if the past output value series {x

t

} is known, then

52

Tang T. and Wang T. (2005).

ANN-BASED MULTIPLE DIMENSION PREDICTOR FOR SHIP ROUTE PREDICTION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 52-59

DOI: 10.5220/0001168200520059

Copyright

c

 SciTePress

try to design a predictor to obtain the future output

value of forward d-step x

t+d

under the condition

of the minimum predictive errors. If x

t+d

is expressed

as , the model of predictor can be described as

follows:

),,()(

ˆ

1

PtXfdx

tt −

= (1)

Where X

t-1

= [x

1

,

x

2

, …, x

t-1

]

T

is the past output

value vector, i.e. historical data.

f (·) is a certain nonlinear function.

P is the parameter set of the system model.

The predictor is called the minimum covariance

optimal predictor, because the covariance of the

predictive error is used for criterion function J as

follows:

min))(

ˆ

( →−=

+

kxxVarJ

tkt

(2)

2.1 RNN-based One-step Predictor

The ANN-based models could be used to construct

an adaptive optimal predictor for model

identification, parameter correction and value

prediction. Assuming that a class of nonlinear

processing can be represented by a nonlinear

autoregressive moving average (NARMA) model,

the NARMA (p, q) model is written as:

tqtttptttt

eeeexxxgx +=

−−−−−−

),,,,,,,,(

2121

"""

(3)

Where is an unknown smooth function, and it is

assumed that E (e

t

│ x

t-1

, x

t-2

,… ) = 0 and e

t

has a

finite variance Var ( e

t

) = σ

2

. In this case, an

approximated condition mean predictor based on the

finite past of observations is given by

(

)

qtttptttt

eeexxxgx

−−−−−−

=

ˆ

,,

ˆ

,

ˆ

,,,,

ˆ

2121

"" (4)

Where

qtttjxxe

jjj

−−−=−= ,,2,1

ˆˆ

"

For NARMA (p, q) modelling and predicting, a

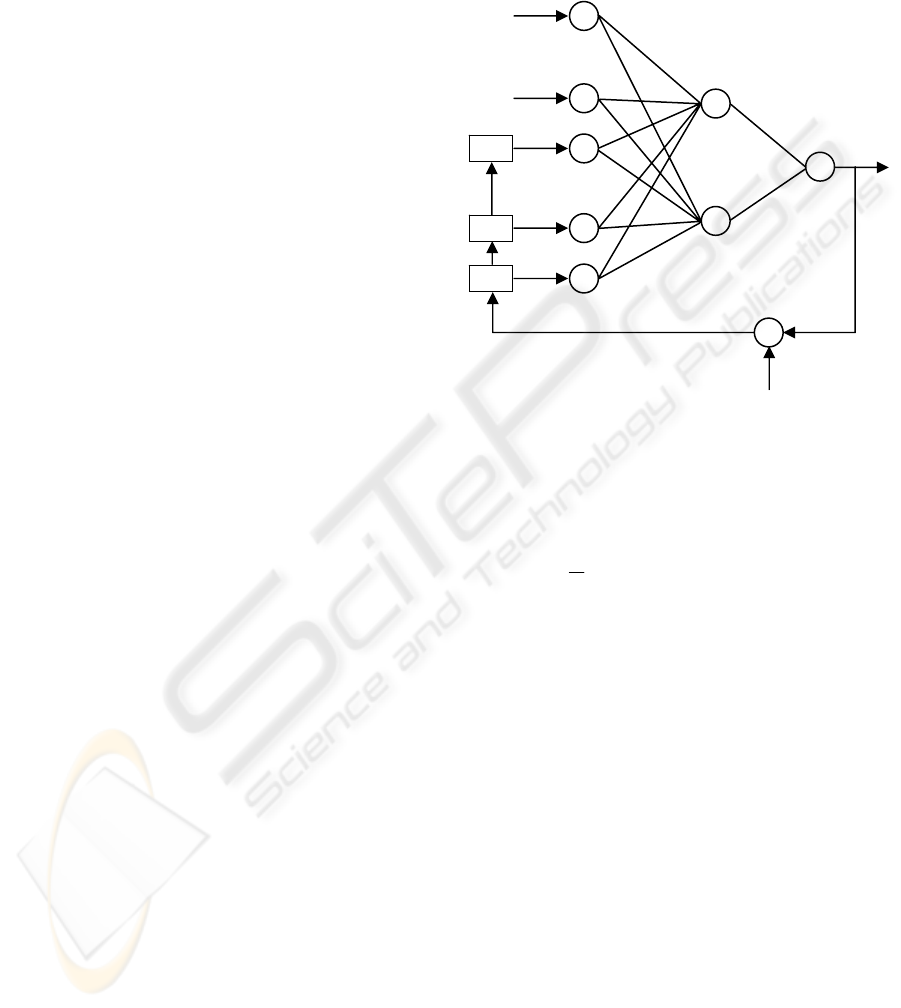
recurrent neural network was presented (Connor,

1994). The recurrent network topology is shown in

figure 1. This recurrent neural network (RNN) can

be used to approximate the NARMA (p, q) model.

The output of the basic RNN-based predictor is

f(s)W

o

=

t

x

ˆ

(5)

θeWxWs

ehih

++= (6)

Where f (⋅) is a Sigmoid function vector or other

finite continuous monotonically increasing function

vectors;

s is a state vector of the hidden layer;

W

ih

is the weight matrix between the input

layer and the hidden layer;

W

eh

is the weight matrix from feedback units

to hidden units;

x is the input vector;

e is the error vector;

θ is a threshold vector.

Figure 1: Recurrent network for NARMA models

The parameters of W

o

, W

ih

and W

eh

are

estimated by a dynamic BP learning algorithm

(Williams, 1990). That is by learning of RNN to

minimize the following error function:

∑

+=

−=

N

pt

tt

xxE

1

2

)

ˆ

(

2

1

(7)

But, just one step prediction will make by the

basic predictor. So some improvement RNN-based

predictors had been discussed (Tang, 2000).

2.2 RNN-based Multi-step Predictor

In order to implement the multi-step prediction, the

NARMA model should be extended to:

()

jdttt

eidXgdx

−+

−=

ˆ

,)(

ˆ

)(

ˆ

(8)

Where

q21jjdxxe

tjdtjdt

,,,,)(

ˆˆ

"=−−=

−+−+

[]

T

ptttttt

xxxdxdxidX

−−

−−=− ,,,,),2(

ˆ

),1(

ˆ

)(

ˆ

1

""

The output of the multi-step RNN model is

f(s)Wx

ot

=

ˆ

(9)

Where

θeWxWs

ehih

++=

)(

ˆ

dx

t

)(⋅g

.

x

t-1

x

t-p

W

i

h

W

eh

W

o

z

-

1

+

-

f

.

z

-

1

z

-

1

f

e

t-q

e

t-2

e

t-1

e

t

x

t

^

x

t

ANN-BASED MULTIPLE DIMENSION PREDICTOR FOR SHIP ROUTE PREDICTION

53

T

dttt

xxx ]

ˆˆˆ

[

ˆ

1 ++

= "

t

x

And the error function is

∑

+=

−−=

N

pt

E

1

ˆˆ

(

2

1

)x(x)xx

tt

T

tt

(10)

Using the dynamic BP learning algorithm, and

assuming that the dimensions of the input, error,

hidden and output matrices could be represented as i,

e, h, and o, the iteration formulae of the weight

values of the RNN prediction model can be obtained

as following:

() ()

W

WW

∂

η

E

kk −=+ 1

(11)

To the weight values of the output layer, there is

t

oh

o

esfI

W

)(

1

)(

∑

+=

×

−=

N

Pt

E

∂

(12)

Where

ttt

xxe

ˆ

−=

(13)

And I is an identity matrix.

To the weight values between the hidden layer

and input layer, there is

∑

+=

×

⋅

∂

⋅

∂

+⊗⋅−=

∂

n

pt 1

)(

)((

t

T

o

T

eh

ih

(h)h)(i

ih

eW

s

sf

)W

W

e

xII

W

E

(14)

Where ⊗ is Kronecker product.

⎥

⎦

⎤

⎢

⎣

⎡

∂

=

∂

−

−−

ihihihih

WWWW

e

qt

tt

e

ee

,,,

21

" (15)

To the weight values of the hidden layer and

feedback units, there is

()

t

T

N

pt

T

t

E

eW

s

sf

W

e

eII

W

eh

hhe

0

1

eh

∑

+=

×

∂

⎟

⎠

⎞

⎜

⎝

⎛

∂

+⊗−=

∂

(16)

Where

⎥

⎦

⎤

⎢

⎣

⎡

∂

=

∂

−

−−

eheheheh

WWWW

e

qt

tt

e

ee

,,,

21

" (17)

3 DRNN PREDICTIVE MODELS

In order to obtain the optimal predictive value of the

future output of the analyzed system based on its

historical data, a stochastic dynamic model of the

analyzed system should be set up, which can modify

the model parameter adaptively. A diagonal

recurrent neural network was used to represent the

dynamic process based on NARMA model (Dou,

2001). The NARMA model is defined as:

)

ˆ

,,

ˆ

,,,,(

ˆ

11121

eexxxhx

tttdt

""

−−−+

= (18)

Where

jjj

xxe

ˆˆ

−= , j = t-1, t-2, …, 1;

h(·) is a nonlinear function.

Figure 2 shows the structure of the DRNN-based

predictive model. The neural network model with

two inputs and several outputs includes three layers.

In order to realize direct multi-steps prediction, the

output layer composes of d linear neural units. And

the middle layer (i.e. hidden layer) makes up NH

nonlinear dynamic neurons whose map function is

the sigmoid function, and each of the hidden unit

includes a self-feedback with one step delay

(recursion layer). The input layer includes two linear

neurons, and one of them accepts x

t-1

as input signal,

another accepts , which is one-step delay of the

output x

t

. This network can be regarded as a

parsimonious version of the Elman-type network. It

has a diagonal structure, that is, there is no

interaction between different dynamic neurons.

x

t

x

t +1

x

t+d

…

=

A

j

W

ij

…

a

1j

a

2j

Figure 2: DRNN-based predictive model

The transfer function of this network is described

as follows. Suppose w

ij

(i =1, 2, …, NH; j =1, 2, …,

d) are the connection weights of the output layer, A

i

(i=1, 2,…, NH) are the connection weights of the

recursion layer, a

1i

(i =1, 2, … , NH) are the

connection weights of the input x

t-1

to each of the

hidden units, a

2i

(i = 1, 2, …, NH) are the connection

weights of the input to each of the hidden units,

the output of the neural unit of the output layer is

expressed as , (j =1, 2,…d), the output of an

neurons of hidden layer is expressed as H

i

( t ), ( i

=1, 2,…, NH), the input of the neural unit of the

hidden layer is expressed as V

i

( t ) (i = 1, 2, …,

1

ˆ

−t

x

1−t

x

z

-

1

z

-

1

ˆ

−t

x

)(

ˆ

jx

t

)(

ˆ

jx

t

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

54

NH), then the map relations of the DRNN are shown

as fellows:

])([)(

ˆ

NH

1

oj

i

iijt

tHwjx

θ

−=

∑

=

(19)

Where

))(()(

hiiNi

tVgtH

θ

−= (20)

)

ˆ

()()1()(

212111

θ

−+−+−=

−− titiiii

xaxatHAtV (21)

is sigmoid function,

θ

oj

is the threshold of

the neural unit of output layer,

θ

hi

is the threshold

of the neuron of hidden layer. The initial conditions

of this model are H

i

(0) = 0 and V

i

(0) = 0. So the

transfer function of the neural network is a nonlinear

continuous function, and the output of the neural

network is an appropriate nonlinear function of

all input signals (x

1

, x

2

, …, x

t-1

).

It is known that the supervised learning

algorithm based on the error between the actual

output and the anticipant output is not suitable for

the direct multi-step predictive model. And a neural

network with the fixed structure and parameters is

difficult or even impossible to express the inherent

dynamic performance of the uncertain nonlinear

systems. For this reason the temporal difference

(TD) learning algorithm and the dynamic back-

propagation (DBP) algorithm are synthesized for the

network training. The combined learning algorithm

will adaptively modify the parameters of the

predictive model according to the errors between the

predictive value and the actual detective value.

Suppose P

t

j

is the output of the jth output

neuron at t time, i.e. , P

t+1

j-1

is the output of

the (j-1)th output neuron at t+1 time, i.e. . It

is obvious that P

t

j

and P

t+1

j-1

are the predictive

output value of the analyzed system at the same

time. And they should be equal if the prediction is

accurate. So the P

t+1

j-1

can be used as the

expectant output of the P

t

j

. This is the basis of

TD learning algorithm. The training error of one

learning sample of the DRNN is expressed as:

∑

=

+

−=

K

j

tjt

jxxe

0

2

))(

ˆ

(

2

1

(22)

According to TD learning algorithm, it can be

expressed as

∑

=

+

−=

K

j

t

j

jxPe

0

21

))(

ˆ

(

2

1

(23)

Here P

0

t+1

is defined as the expectant output of x

t

at t time.

4 A MULTI-DIMENSION

PREDICTOR BASED ON

PDRNN

One dimension predictive model can predict an

object with one kind of attribute. A multi-dimension

predictive model can predict an object with more

than one kind of attribute at the same time. In the

multi-dimension predictive model, there are

different relations in different attributes and the

relations can be changed by a dynamic process. For

this reason, ANN-based adaptive predictors must be

introduced to modify the parameters of a predictive

model on-line.

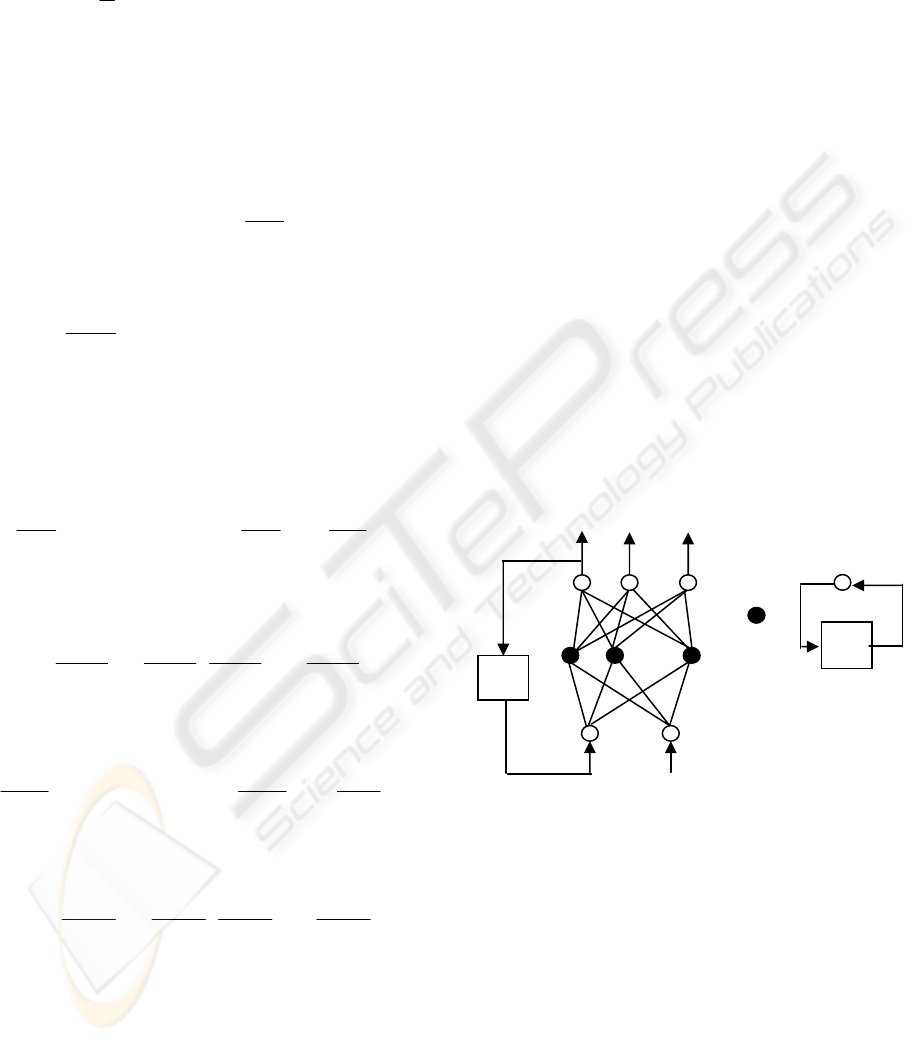
4.1 The Framework of PDRNN

Model

In order to solve the predictive problem of objects

with multi-attributes, this paper presents a new

multi-dimensional predictive model based on

the

diagonal recurrent neural networks (PDRNN) with a

parallel combined learning algorithm. Fig. 3 shows

the framework of PDRNN model. There are four

layers in this model, the first layer is the network

input layer; the second layer is the network input

assignment layer; the third layer is the network

hidden layer, in which every hidden unit includes a

self-feedback with one step delayed; the forth layer

is the network output layer, (the network output

layer connects with the network input layer through

one-step feedback). There are n dimension variables

to input paralleled in the network input layer. It

solves the problem that only one variable can be

input in some one dimension predictive models, and

the PDRNN model can predicts an object with

multiple variables and attributes.

4.2 The Mathematical Description of

the PDRNN Model

As shown in figure 3, there are p input units in the

network input layer, every input unit has n

dimension variables, can be obtained by with

one step delayed, so each attribute variable has p-1

input values in this network every time in fact. The

network input assignment layer assigns n values of

each variable to n sub-input layers paralleled, as

shown in equation (24). The hidden layer has n sub-

hidden layers paralleled, every sub-hidden layer has

)(

ˆ

jx

t

)(

ˆ

jx

t

)(

ˆ

jx

t

X

1+t

Z

)(⋅

N

g

ANN-BASED MULTIPLE DIMENSION PREDICTOR FOR SHIP ROUTE PREDICTION

55

NH

1

(the number of sub hidden layer) nonlinearity

units with S functions or T functions, the value of

NH

1

can be changed, and every sub-hidden layer has

self-feedback with one step delayed. In this network,

n paralleled sub-networks consisted of the sub-input

layers and sub-hidden layers, all the parallel sub-

networks respectively train different attributes at the

same time. This network neglected the relations in

the different attributes and attribute values. There

are k linear units in the network output layer, which

can do d-step prediction at most. The mathematical

model could be described as follows:

The network input layer

],,,[

1 pttt

XXX

−−

"

Where

[

]

n

tttt

XXXX ,,,

21

"= (24)

The Ith parallel sub-network’s sub input layers:

[

]

I

pt

I

t

I

t

XXX

−−

,,,

1

" (25)

The I th parallel sub-network’s sub hidden

layers:

))(()( tVgtH

i

I

N

i

I

=

(26)

In equation (26), at every t time, is the

output of the ith hidden unit in the Ith parallel sub-

network, is Sigmoid (S) function or Tangent

(T) function. And there:

∑

=

−

+−=

I

i

t

I

i

I

i

I

i

I

i

I

XwtHAtV

N

1

)1()( (27)

In equation (27), at every t time, is the sum

of all the inputs in the ith hidden layer of the I th

parallel sub-network, is the normalized (relative)

fulfilment weights between the sub-input layer and

sub-hidden layer of the I th parallel sub-network,

is the self-recurrent layer’s relative weights of the ith

hidden unit in the I th parallel sub-network. is

defined as the output of the j th output unit and

includes all the attribute values at this time. So the

output variables of the network model could be

written by equation (28) as below:

⎜

⎝

⎛

=

∑∑

==

+

12

NH

1

NH

1

2211

),(),(

ii

iijiij

jt

tHatHaZ

⎟

⎠

⎞

∑

=

n

i

n

ij

n

tHa

NH

1

)(," (28)

Where

∑

=

+

=

I

i

I

i

I

ij

I

jt

tHaZ

NH

1

)(

is the jth output layer’s output of the I th attribute at

t time. In the initialization, the threshold value of all

the nerve units were neglected at every t time, and

0)0( =

i

I

H

)(tH

i

I

)(⋅

N

g

I

W

I

i

A

jt

Z

+

)(tV

i

I

Figure 3: Multi-dimension predictive model based on PDRNN

…

1+t

Z

2+t

Z

kt

Z

+

t

X

1−t

X

pt

X

−

t

X

2

t

X

1

t

X

3

1

2

−t

X

1

−t

X

1

3

−t

X

pt

X

−

2

pt

X

−

1

pt

X

−

3

1−

z

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

56

5 THE LEARNING ALGORITHM

This paper combines the time different method (TD)

and dynamic BP method to train PDRNN model. If

as the

jth output of the Ith attribute at t time,

is the predictive value of the

Ith attribute at t+j time,

is real value of the

Ith attribute at t+j time in

the future.

In the ideal condition, is equal to ,

but usually there are some errors in practice. It could

be represented by following error function.

()

2

0

2

1

∑

=

+

−=

kN

j

I

jt

II

I

ZXe (29

)

Equation (29) is the training error of the

Ith

attribute at

t+j time. Here use a dynamic BP method

to correct relative weighs. The learning algorithm is

as follows

()

)(tHXZ

a

X

e

a

e

i

I

jt

I

jt

I

ij

it

I

it

I

ij

I

++

+

−−=

∂

=

∂

(30)

Where are the normalized (relative) fulfilment

weights between the sub hidden layer and sub output

layer of the Ith paralleled sub-network.

The formula corrected of as follows:

)()()(

)()1(

tHZXta

a

e

tata

I

i

I

jt

I

jt

II

ij

I

ij

I

II

ij

I

ij

++

−+=

∂

−=+

ξ

(31)

Where is learning parameter of the Ith attribute’s

output layer, is the normalized (relative)

fulfilment weights between the sub input layer and

sub hidden layer of the Ith paralleled sub-network.

∑

=

++

+

=

+

∂

−−=

∂

−=

∂

kN

j

I

ij

I

i

I

ij

I

jt

I

jt

ij

I

i

I

i

I

it

I

kN

j

it

I

ij

I

w

H

wZX

w

tH

X

e

w

e

0

)(

(32)

The formula is corrected for as follows:

)()()(

)()1(

0

tQaZXtw

w

e

twtw

I

ij

I

ij

kN

j

I

jt

I

jt

II

ij

I

ij

I

II

ij

I

ij

I

∑

=

++

−+=

∂

−=+

η

(33)

Where is learning parameter of the Ith attribute’s

input layer;

are the self-recurrent layer’s relative weights.

)()(

)(

0

tPaZX

A

tH

X

e

A

e

I

i

I

ij

kN

j

I

jt

I

jt

i

I

i

I

i

I

it

I

kN

j

it

I

i

I

∑

=

++

+

=

+

−−=

∂

−=

∂

(34)

Where

I

i

I

i

A

e

P

∂

=

, and 0)0( =

I

i

P .

The formula corrected of

I

i

A as follows:

I

i

I

ij

kN

j

I

jt

I

jt

II

i

I

i

I

II

i

I

i

PaZXtA

A

e

tAtA

I

∑

=

++

−+=

∂

−=+

0

)()(

)()1(

µ

(35)

Where is the learning parameter of the Ith

attribute’s self-recurrent layer.

First is to adjust the network framework, make

sure of the number of input layers, hidden layers and

output layers, and the number of maximal learning

steps. The above parameters are significant for

predictive accuracy. Second initialize the network

(for new data, the initialization is random), then

ANN begins learning. Equation (29) serves as a

standard to judge the predictive value of each

attribute. In order to avoid the learning of ANN

falling into a dead area, the learning step could be

adjusted according to different attribute values. Here

a “

e

” function was presented, equation (36) serves

as a standard to judge the predictive values of all the

attributes.

∑

=

−

=

n

kt

t

E

kn

e

1

(36)

And

∑

=

m

I

tt

eE

1

2

)( (37)

Where is the error between the real value and the

predictive value of the Ith attribute at t time, can

be changed according to different attributes.

e

is

the average error, used to judge the convergence of

the multi-dimension predictive model based on

PDRNN. Because the initialization of ANN is

random, the first couple of predictive values may be

not very good,

e

is computed from the kth

predictive value. The training will be stopped when

jt

I

Z

+

jt

I

X

+

jt

I

Z

+ jt

I

X

+

ij

I

a

ij

I

a

I

ξ

ij

I

w

ij

I

w

I

η

I

i

A

I

µ

I

t

e

t

E

ANN-BASED MULTIPLE DIMENSION PREDICTOR FOR SHIP ROUTE PREDICTION

57

e

is up to standard, or reset up the network

framework until

e

confirms to requirements.

6 SIMULATIONS AND

APPLICATION

The prediction based on PDRNN extends ANN-

based time series prediction model from a single

attribute to a multi-attribute. Figure 4 is a three-step

predictive value contrasting with real values of

straight line, real lines are real values, “*” indicates

the predictive values. The points of straight line have

two kinds of attributes, every parallel sub-network

has ten sub input layers and fifteen sub hidden

layers. T function is used in the hidden units, the

maximum of e is 2.265e

-5

,

e

is 8.36e

-8

.

Figure 5 is a three-step predictive value of

nonlinearity as follows:

⎭

⎬

⎫

⎩

⎨

⎧

<≤

<≤×

=

ππ

π

42,)(

20,2

xxSin

xx

y

Figure 6 is a three-step predictive value of 3D curve

contrasting with real value, T function is used in the

hidden units, every parallel sub-network only has ten

sub input layers and fifteen sub hidden layers. The

learning step of 3D curve is more than 2D curve.

The maximum predictive error of 3D curve is

0.0011,

e

is 8.265e

-4

.

An application process for GIS in Marine

Engineering with the predictor based on PDRNN is

shown in figure 7.

In the system, data recorded abundant ship

positions from GPS, and established a database

through ACCESS. The software of GIS is ArcView

3.2 of ESRI (Goodchild, 1992). ArcView 3.2 called

the data from ACCESS, and eliminated unnecessary

data by applying ArcView 3.2. After data pre-

processing, the ship route could be selected and

drawn in an electronic chart. Using the PDRNN

predictor the tracking of the ship route could be

forecasted.

The process of ship route prediction by means of

a PDRNN model is as follows: first, get the

distribution data of the ship’s position from GPS

(Wang, 2003), then select sample points. In this

Figure 7: GIS in Marine Engineering

S

teering

Ships

D

isposing

by Com-

puter

P

redicting

Ship

Route

Collecting

Ship'

s

P

osition

GPS

Figure 4: Predictive value contrasting

Figure 5: Prediction of nonlinearity

Figure 6: Prediction of 3D curve

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

58

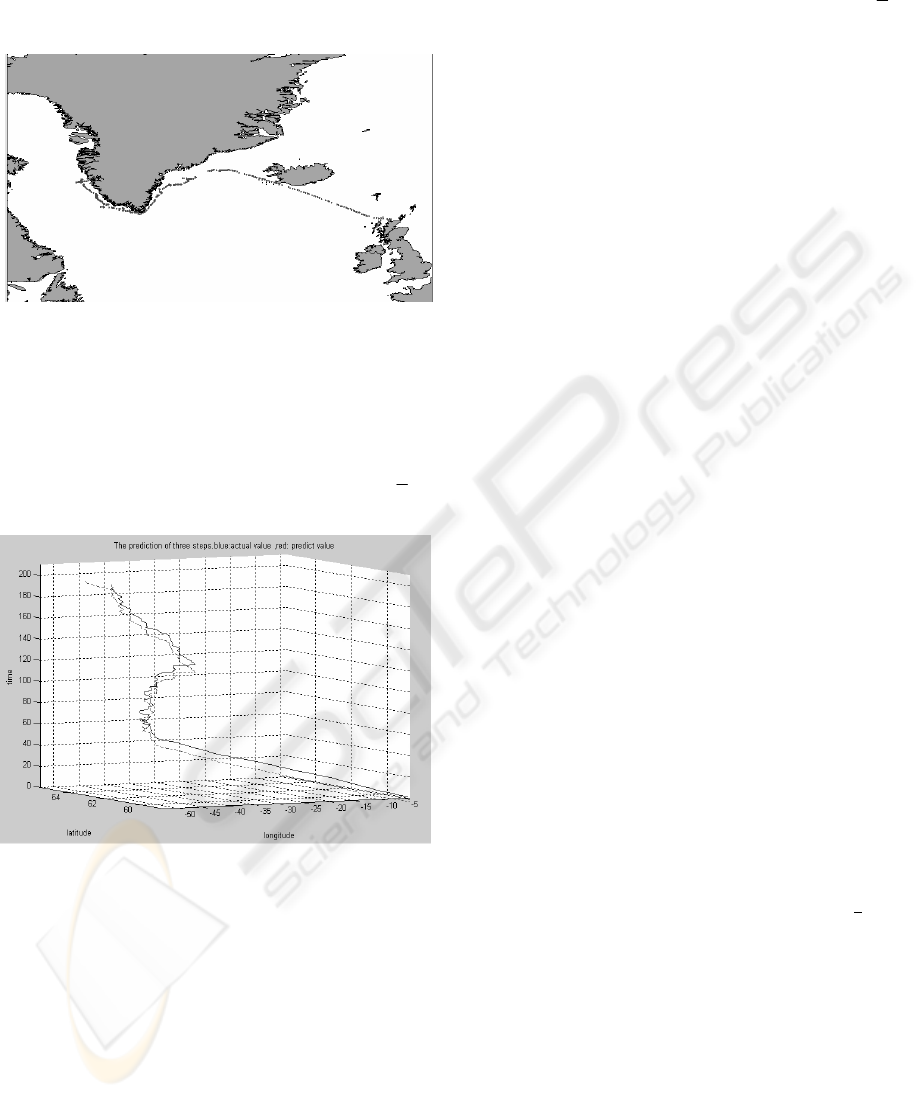
paper, the each sample point was selected every 2.5

hours. Figure 8 is a selected ship route. Finally, the

ship route was predicted by means of a PDRNN

model.

Figure 9 is another prediction resolve of a ship

route. This chart shows that this ship route is a

variant random process, but the predictive algorithm

based on a PDRNN model can follow this process,

and do three-step prediction. The predictive

maximum error of the ship route is 1.065e

-14

,

e

is

3.326e

-15

. Thus the error of prediction is small.

7 CONCLUSIONS

As mentioned above, the NARMA models based on

the recurrent neural networks with a dynamic BP

algorithm is suited for trend prediction. This paper

presents a multi-dimension predictive model based

on PDRNN. This predictor could store in memory

all the past input information, network output is

some nonlinear function of all the past input, and

this model can realize a nonlinear dynamic mapping.

As a predictive model, the framework is very

simple, the dynamic behavior of this model could

regulate network frameworks with self-adaptation,

and this model could predict an object with multi-

attribute. Moreover, this paper has presented an “

e

”

function, which can judge if the whole network

structure confirms to requirements, and has

presented an “input plus” method, which can reduce

the training time. The application in ship routing

prediction shows the new predictive model is better

to predict a multiple dimension dynamic process.

REFERENCES

Box, G. E. P. And Jenkins, G. M., 1970. Time series

analysis of forecasting and control

. Holden-day, San

Francisco.

Connor, J. T., Martin R. D. and Atlas L. E., 1994.

Recurrent neural networks and robust time series

prediction. In

IEEE Trans. on neural networks, No.5,

p. 240-254.

Dou, J. and Tang, T., 2001. A DRNN-based direct multi-

step adaptive predictor for intelligent systems. In

Proceedings of the IASTED International Conference

on Modelling, Identification, and Control

, vol.2,

p.833-838, Innsbruck, Austria.

Goodchild, M. F., 1992. Geographic data modeling. In

Computers and Geosciences, Vol. 18, No. 4, pp.401-

408.

Tang, T.

et al., 1998. ANN-based nonlinear time series

models in fault detection and prediction. In

Preprint of

IFAC Conference on CAMS'98

, p.335-340, Fukuoka,

Japan.

Tang, T. et al., 2000. A RNN-based adaptive predictor for

fault prediction and incipient diagnosis. In

UKACC

Control 2000

, Proceedings of the 2000 UKACC

International Conference on Control

. Cambridge, UK.

Wang, T., Hao, R. and Tang, T., 2003. A data mining

method for GIS in marine engineering. In

Navigation

of China

. No. 3, p.1-4.

Williams, R. j. and Peng, J., 1990. An efficient gradient-

based algorithm for on-line training of recurrent neural

networks. In

Neural Computation, No.4, p.490-501.

Wittenmark, B. A., 1974. A self-tuning predictor.

IEEE

Trans. on Automatic Control

, No.6, p.848-851.

Figure 8: The ship route

in GIS

Figure 9: The prediction of ship route

ANN-BASED MULTIPLE DIMENSION PREDICTOR FOR SHIP ROUTE PREDICTION

59