HIGHLY ACCURATE INTEGRATION OF TRACK MOTIONS

Michael Kleinkes, Angela Lilienthal, Werner Neddermeyer

University of Applied Science in Gelsenkirchen

Neidenburger Str. 43, 45897 Gelsenkirchen

Keywords:

Industrial Robots, 7

axis, linear track, ofﬂine programming.

Abstract:

According to the largeness of the workpieces in several industrial environments, a great number of industrial

robots is placed on external track motions, so called 7

axes, as for automotive or aircraft industries. Flexible

automation today requires absolute high accuracy. For example modern robotics deals with ofﬂine program-

ming, copying programs between similar working cells, reﬂecting programs or image processing for 3D-pose

estimation. All these tasks need absolute high accuracy and in fact, there have been many investigations for

increasing the accuracy of single robots in the past few years.

In contrast to that the use of track motions will dramatically increase the position error and badly inﬂuence

the static behaviour of the robot system. The main reasons for these additional errors are the incorrect identi-

ﬁcation of the main track direction and furthermore, very crucial, the non-linearities of the TCP (Tool Center

Point) during the robots motion on the track. This article will introduce a new method of identiﬁcation and

mathematical integration of linear tracks. At ﬁrst we present the method for measuring and generating proﬁles

of single tracks by making use of the discrete fourier transformation (DFT) and cubic spline interpolation.

Then a method for recalculating ofﬂine generated programs for real environments is presented, followed by a

method for copying programs taking two proﬁles of track motions into consideration. Finally some measure-

ment results are shown.

1 INTRODUCTION

Increasing demands on the ﬂexible automation, e.g.

ofﬂine programming of robot motions or the applica-

tion of more and more complex tasks like sealing of

carbodies, require robot systems with absolute high

accuracies. In the past there was done a lot of re-

search work and investigations to increase the accu-

racy of robots by an individual identiﬁcation (Denavit

and Hartenberg, 1955), (Maas, 1997) of internal para-

meters, so that robots with a high accuracy option are

available (Nitschke, 2002). From the experience the

inaccuracy of these robots is almost less than 1 mm.

In many cases of the automotive industry, the ro-

bot’s workspace is extended by external track motions

which deteriorates the accuracy of the system in a

signiﬁcant manner about several millimetres or more.

This alarming fact is not compatible to the demands

on the ﬂexible automation at all and additionally is ne-

glected by scientists and robot manufactorers as well.

Ofﬂine programming, copying or reﬂecting pro-

grams or 3D pose estimation requires a coordination

of the track and the robot motion, that means an inte-

gration into the robots coordinate system. The meth-

ods of measurement, identiﬁcation and mathematical

integration of track motions are shown exemplary for

an ABB robot. Similar computations for other types

of robots, e.g. KUKA or FANUC, are possible as

well. Figure 1 will give you an overview of the im-

portant robot coordinate systems.

The alignment frame, as shown in ﬁgure 1, pro-

vides the connection of the track motion to the robot.

The ABB controller is computing the main track di-

rection from a frame containing quaternions (Convay

and Smith, 2003), which indicates the rotation from

the robot’s world frame to the track. It is obvious,

that the similar parameters for the track integration

have to be worked out for each type of robot, e.g.

KUKA, COMAU or FANUC. It is an essential knowl-

edge, that any type of controller unit is modelling

tracks as straight lines, where the incorrect identiﬁ-

cation of the main track direction and - very crucial

- the non-linearities of the robot’s TCP during a mo-

tion on the track, the so called robot’s twist, are not

Kleinkes M., Lilienthal A. and Neddermeyer W. (2005).

HIGHLY ACCURATE INTEGRATION OF TRACK MOTIONS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 11-15

DOI: 10.5220/0001169100110015

 SciTePress

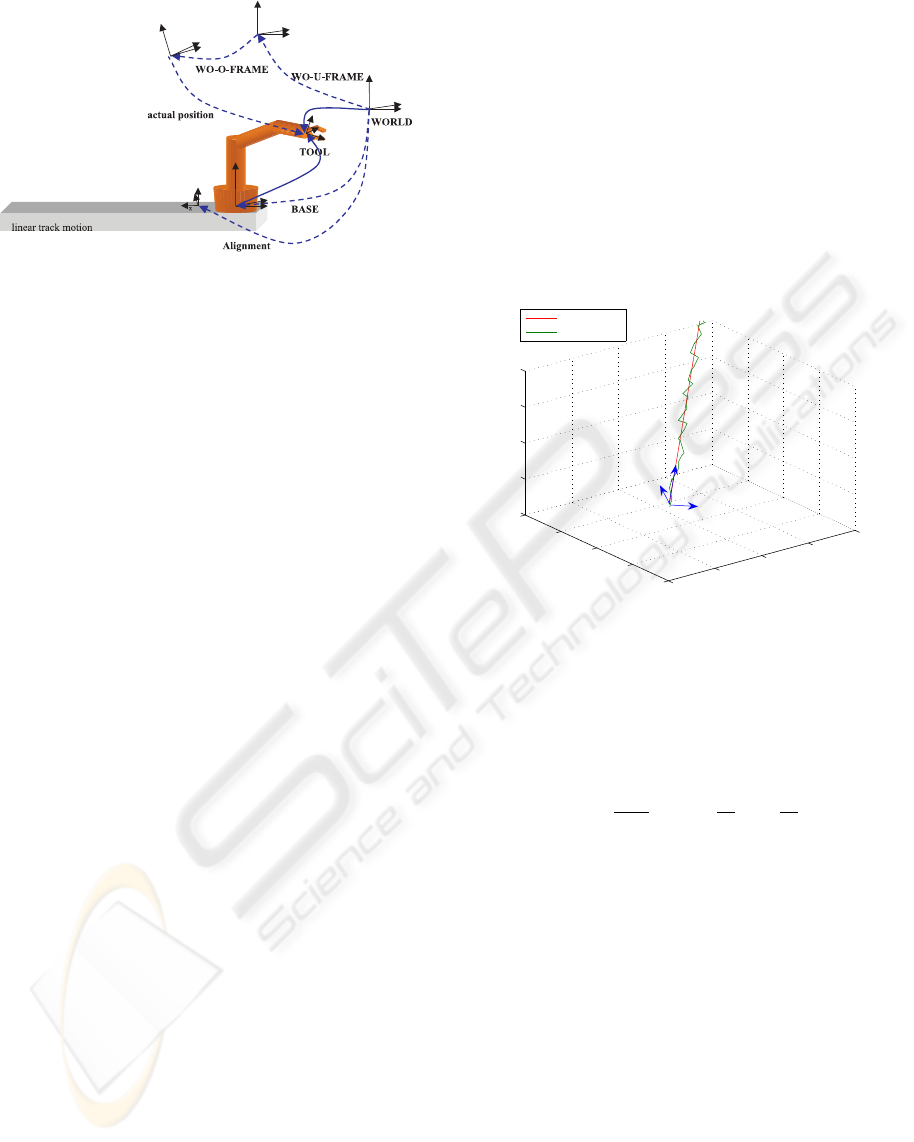
Figure 1: Coordinate systems

taken into consideration. The ofﬂine generated robot

motions, the actual positions, are related to the work-

piece, which is provided by the so called workobject

(WO-U- and -O-FRAME) of the robot controller in-

terface.

2 IDENTIFICATION OF TRACK

MOTIONS

For the identiﬁcation of track motions we make use

of a mobile coordinate measurement device, e.g. a

laser tracker. Due to the computation of the robot’s

behaviour under motion on the track, it is aimed to

identify the robot’s coordinate system at n positions.

For that, ﬁrst the optimal number of positions is to be

found by the spectral analysis (Press et al., 1989) of a

ﬁne scanned motion.

2.1 Fine scanning

For the evaluation of the optimal number of posi-

tions where a frame identiﬁcation is necessary, a sin-

gle high resolution scan of the robots TCP during a

motion on a straight line with constant joint conﬁg-

uration, that means movement only by the track, is

generated. The movement is carried out with low and

constant velocity V and the scan mode is switched on

high resolution and discrete in time (sampling inter-

val: dt).

Assuming that one axis of the measurement frame

points in the direction of the expected line, the sum

of the 3D coordinates x

, y

and z

contains the

command function - a ramp function s

- plus the

non linear twist motion, which is of interest. After

the elimination of the ramp function, the Fourier

transform of the h

’s contains the spectrum of the

non-linearities of the track:

From

= k · ∆, k = 0, 1, ..., N − 1 (1)

and

∆ = V · dt (2)

follows

= x

+ y

+ z

− s

(3)

where the x

, y

and z

are the 3D scan of the TCP

(see ﬁgure 2).

command line

error motion

measurement frame

Figure 2: command and error motion

The DFT becomes

H(f

) = X(f

) + Y (f

) + Z(f

) − S(f

) (4)

from

N∆

; n = −

, ....,

(5)

follows that

H(f

) =

∞

−∞

h(s)e

−j2πf

≈

N−1

k=0

−j2πf

∆

= ∆

N−1

k=0

−j2πkn/N

(6)

From eq.5 it is obvious that the frequency is of the

unit mm

−1

Figure 3 gives an example about a spectrum taken

from a typical arrangement.

If a detection of errors greater than 0.5 mm is re-

quired, it is obvious by the sampling theorem that it is

essential to identify the robot coordinate frame each

100 mm (= 1/(2 · 0.005mm

−1

)).

ICINCO 2005 - ROBOTICS AND AUTOMATION

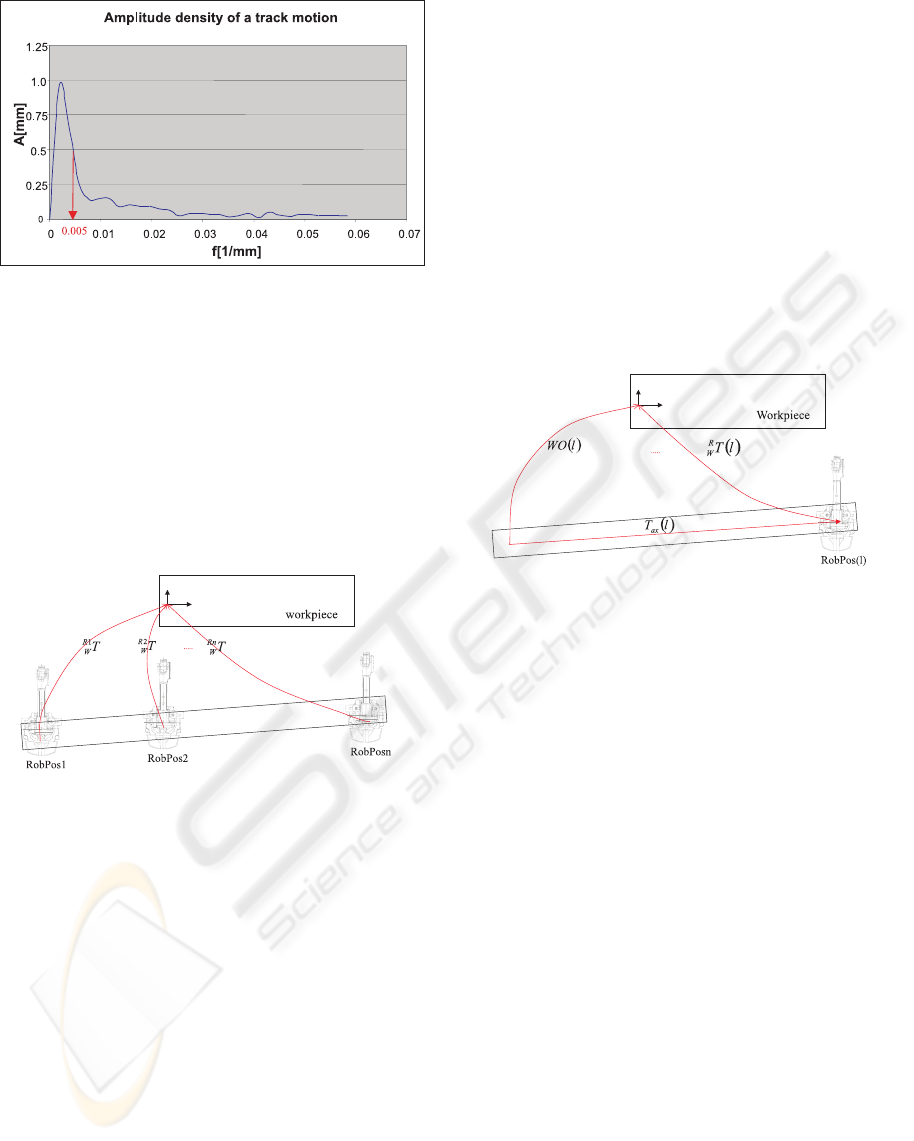
Figure 3: Example of a track spectrum

2.2 Generation of track proﬁles

Once the sampling rate is known, it is possible to gen-

erate the continuous of the non-linear robot behaviour.

At ﬁrst the robot’s coordinate frame is identiﬁed at n

positions on the track. The measurements are done

using the same set up points at each position. That

means the robot is taken as a rigid body, because of

it’s high repeatability.

Figure 4: Measurement of the axis proﬁle

Figure 4 shows the relations if the workpiece, to

which the ofﬂine generated programs are related to, is

already identiﬁed. The results are n transformations

where the six dimensions of freedom are implicitly

dependent on the value of the track:

T = f

(α(l

), β(l

), γ(l

), t

))

(7)

For the computation of a continuous description, we

make use of the cubic spline interpolation procedure

(Dautray, 2000), which connects the discrete pairs of

varieties (α

, l

), (β

, l

), etc. to smooth and also

smooth in the ﬁrst derivative functions, so that the

continuous form becomes:

T (l) = f (α(l), β(l), γ(l), t

(l), t

(l)) (8)

Note, that these are the relations where the track is

not coordinated to the robot motion. For a connection

to the robot base, the axis transformation, which is

dependent on the value l of the robot’s position on the

track as well, is computed by:

(l) =







I l ·

Dir







(9)

where I is the 3 × 3 identity matrix and

Dir

the controller owned normalised axis direction (which

has to be worked out individually belonging to the

type of robot). From eq.8 and 9 the workobject frame

W O(l) becomes:

W O(l) = T

(l) ·

T (l) (10)

which is shown in ﬁgure 5.

Figure 5: Connection to track motion

3 MODIFICATION OF ROBOT

PROGRAMS

The modiﬁcation of robot programs has to be divided

into two parts. The ﬁrst case is copying ofﬂine gen-

erated motions to a real proﬁle, whereas the second

is copying programs between similar working cells

taking both - the master and the slave - proﬁle into

consideration.

3.1 Modulation of ofﬂine generated

robot programs

In ﬁgure 6 you can see the robot’s behaviour under

a motion on it’s 7

axis. Note that the predeﬁned

controller owned workobject is WO1 which is valid

for the robot position RobPos1 without moving on the

track. But under robot motion and it’s twist it points

from the position RobPos n to the dashed workpiece

which of course is not there.

From the splined workobject and the actual value

on the track we know all relations, so as a conse-

quence the corrected workframe becomes:

corr

= (W O1)

−1

· W O(l) · T

offline

(11)

HIGHLY ACCURATE INTEGRATION OF TRACK MOTIONS

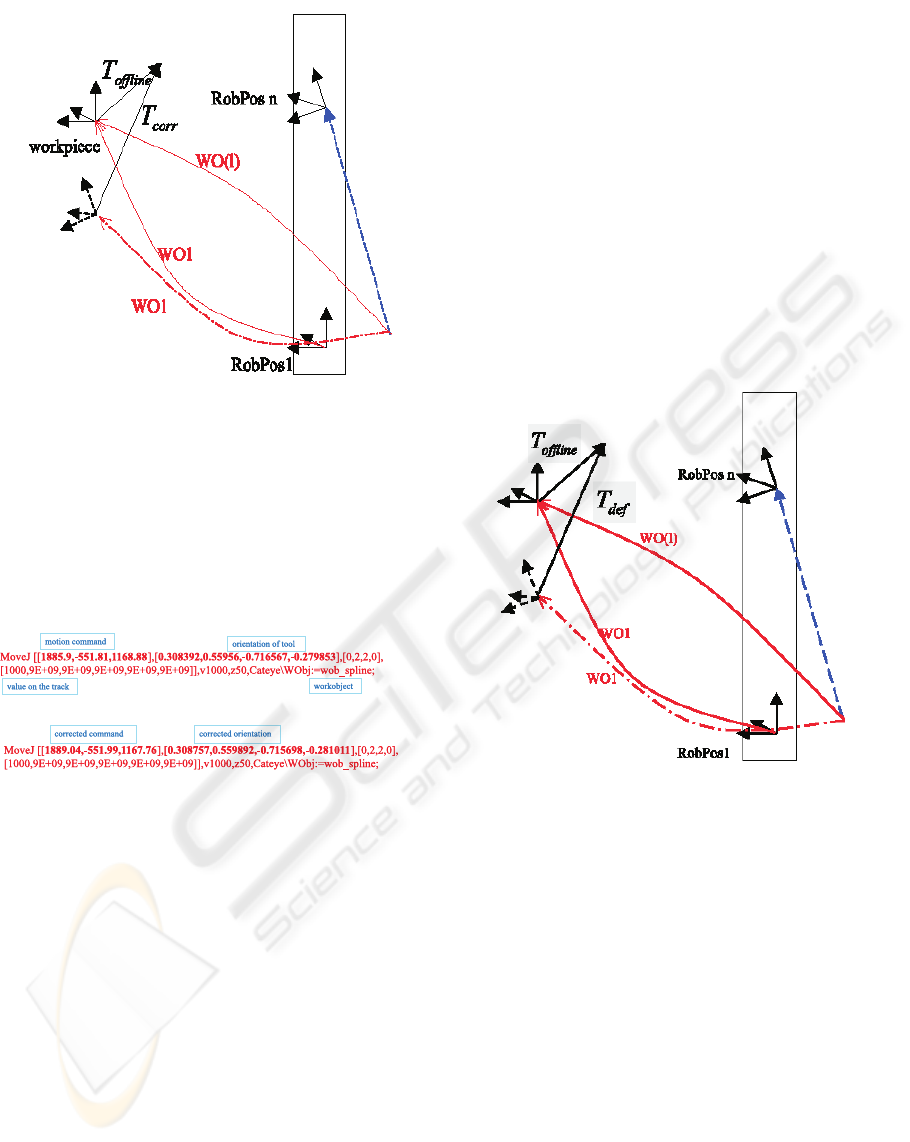
Figure 6: Workobjects and twist

The example shown in ﬁgure 7 illustrates the modiﬁ-

cations to the motion commands in the robot language

RAPID, which is characteristic for ABB robots.

Figure 7: Modiﬁcation of robot commands

The motion commands are always related to the

coordinate system of the workpiece and the orienta-

tion of the tool is - a speciality of ABB robots - ex-

pressed in quaternion notation. The value on the track

has to be given explicitly for each robot motion, be-

cause of the overdetermination of the inverse problem

when using a 7

axis - that means for sure an ad-

ditional degree of freedom. The choice of the prede-

ﬁned workobject is individually possible for any com-

mand.

So- what the proposed procedure does is just to re-

place the motion commands - translation and orien-

tation - with the corrected ones. That means that the

corresponding software tools won’t change the struc-

ture of the robot ﬁle. It will be a kind of artiﬁcial post

teaching of robot programs.

3.2 Copying programs between

similar robot systems

From chapter 3.1 we are able to modify ofﬂine gen-

erated robot ﬁles with the behaviour of the real robot

and due to that, create accuracies for the robot sys-

tems, which are rather identical to those of single ro-

bots.

But what is to be done if two track motions are

of interest in the case of copying programs from one

station to another? The solution is the computation

of so called quasi ofﬂine programs under considera-

tion of the track from which the programs should be

copied. That means: compute the inverse of the de-

scribed method as illustrated in ﬁgure 8.

Figure 8: Copy programs

Now the deﬁned or teached workframes T

def

of the

robot master are known which have to be recalculated

into an ideal perpendicular ofﬂine world (T

offline

= (W O(l))

−1

· W O1 · T

def

(12)

These quasi ofﬂine generated programs from the ro-

bot master proﬁle can be taken as the input ﬁles for

the method described in chapter 3.1 to create the con-

verted motions for the slave system.

4 RESULTS

Figure 9 illustrates the results of a test program con-

taining 12 work frames. The blue columns show the

errors of the conventional robot system whereas the

red ones show the errors of the modiﬁed workframes.

ICINCO 2005 - ROBOTICS AND AUTOMATION

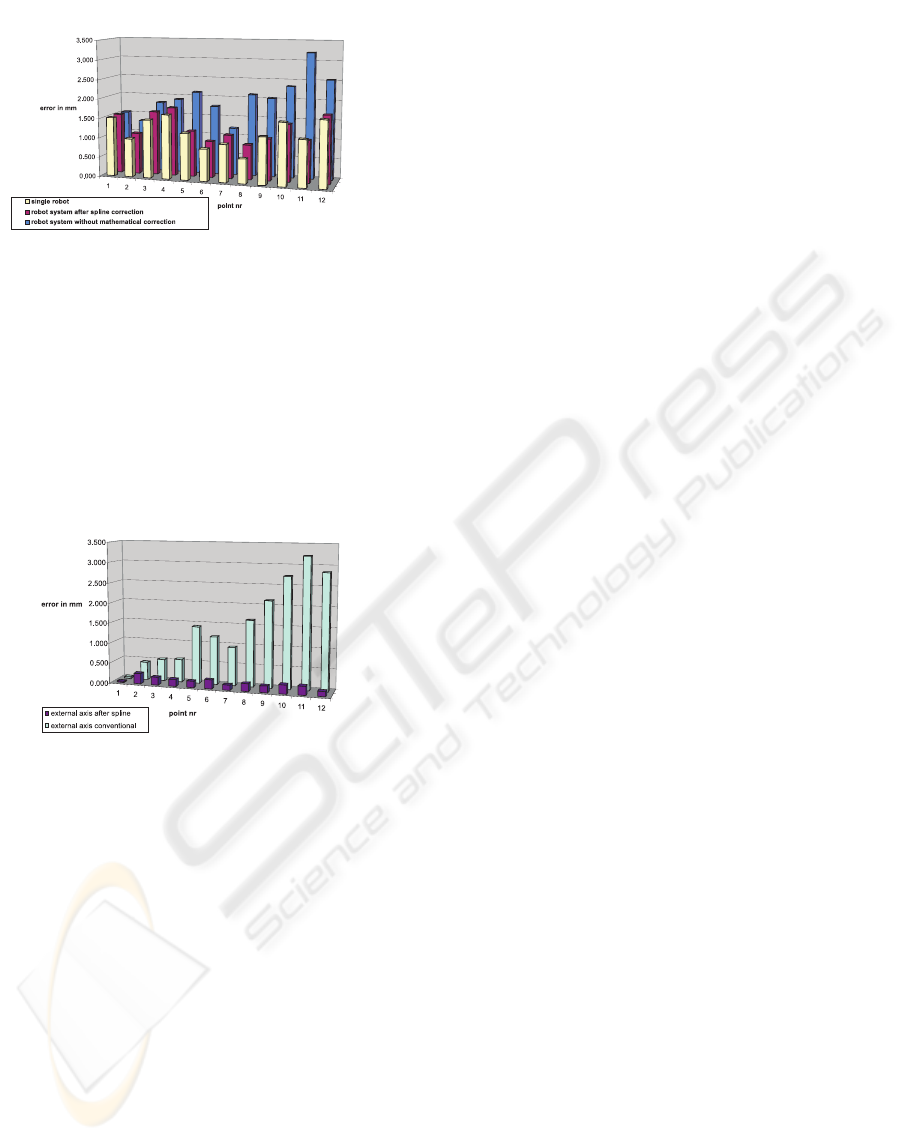
Figure 9: Results 1

For a validation the yellow ones show the errors of the

robot itself.

So the ﬁnal improvement is demonstrated by ﬁgure

10. The errors caused only by the track are shown

by the bright blue columns for the conventional sys-

tem and - the dark blue ones - for the modiﬁed robot

motions.

Figure 10: Results 2

5 CONCLUSION

As a conclusion we want to emphasise the compensa-

tion of errors caused by external track motions. That

means the

• accuracy of the robot system is nearly identical to

that of the single robot.

• the worst case for the inaccuracy of copied pro-

grams is the doubled inaccuracy of one single ro-

bot.

A future prospect will be the implementation into

the robot control, that means including the measured

splines directly into the position control of the robot

as an option for high accurate robots. A further step

will be the implementation into continuous path mo-

tions.

REFERENCES

Convay, J. and Smith, D. (2003). On quaternions and octo-

nions. A K Peters, Massachusetts.

Dautray, R. (2000). Mathematical analysis and numerical

methods for science and technology. Springer, Lon-

don.

Denavit, J. and Hartenberg, R. (1955). A kinematic nota-

tion for lower-pair mechanism based on matrices. In

ASME Journal of Applied Mechanics 22, pages 215–

221.

Maas, H. G. (27.7.-1.8.1997). Dynamic photogrammetric

calibration of industrial robots, spie’s 42 annual meet-

ing, san diego. In Videometrics V, SPIE proceedings

Series Vol. 3174.

Nitschke, H. (2002). Zur Bestimmung geometrischer Pa-

rameter von Industrierobotern. Bayrische Akademie

der Wissenschaften, Dissertation, TU Munich.

Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flan-

nery, B. F. (1989). Numerical Recipes in C. Cam-

bridge University Press.

HIGHLY ACCURATE INTEGRATION OF TRACK MOTIONS