A NEW APPROACH TO AVOID OBSTACLES IN MOBILE ROBOT

NAVIGATION: TANGENTIAL ESCAPE

Andre Ferreira, Mario Sarcinelli Filho and Teodiano Freire Bastos Filho

Department of Electrical Engineering

Federal University of Espirito Santo

Av. Fernando Ferrari, 514

29075-910 Vitoria-ES, BRAZIL

Keywords:

Mobile robots, Robot control, Obstacle avoidance, Impedance-based control, Tangential escape.

Abstract:

This paper proposes a new strategy for obstacle deviation when a mobile robot is navigating in a semi-

structured environment. The proposed control architecture is based on a reactive approach, thus demanding

low computational effort. It allows the robot to navigate from a starting point to a destination point without

colliding to any obstacle in its path. The deviation from an obstacle is performed according to an escape angle

calculated so that the new robot orientation is tangent to the obstacle. It is shown that such strategy generates

more efﬁcient trajectories, in the sense that the destination point is reached in less time while saving energy and

reducing the demand on the robot motors. Another meaningful feature of the proposed strategy is that it also

allows to implement the behaviors Wall Following and Corridor Following with no additional computation.

1 INTRODUCTION

When a mobile robot is navigating in an unstruc-

tured environment it is very important to assure that

it will not collide to any obstacle. Several meth-

ods, like Edge Detection (Kuc and Barshan, 1989),

Certainty Grid (Elfes, 1987), Potential Field (Khatib,

1986), Virtual Force Field (VFF) (Borenstein and Ko-

ren, 1989), Vector Field Histogram (VFH) (Boren-

stein and Koren, 1991) and Nearness Diagram (ND)

(Minguez and Montano, 2004), have been used to

avoid obstacles in mobile robot navigation. Some of

them are tailored for reactive navigation and others

are more suitable to deliberative navigation, where a

map of the robot working environment is built (Fox

et al., 1997; Brock and Khatib, 1999; Althaus and

Christensen, 2002).

The VFH, VFF and Certainty Grid methods are tai-

lored for deliberative navigation. They use data com-

ing from the robot sensors to build a detailed map of

the environment, which is used to plan the trajectory

the vehicle should follow. Such methods generally

require a lot of computation and loose effectiveness

upon any change in the robot working environment.

Regarding reactive navigation, the robot has no a

priori knowledge about the environment surrounding

it, except, perhaps, that it is a plain indoor environ-

ment. Then, to plan a trajectory is not possible, since

a map of the environment is not available. The idea is

that perceptions are tightly related to actions, result-

ing in simplicity and low computational effort. Envi-

ronmental changes are not a problem as well, when

reactive navigation is adopted. Therefore, reactive

navigation is more suitable to semi-structured envi-

ronments, while deliberative navigation is more suit-

able to structured environments. The Edge Detection

and the Potential Field methods, among those previ-

ously mentioned, are methods compatible to reactive

navigation.

This paper recalls obstacle avoidance in mobile ro-

bot navigation, and proposes a new approach to this

topic, as it will be detailed in the sequence. For be-

ing extensively used as a reactive control architecture,

the Impedance Based Control (Hogan, 1985; Secchi

et al., 2001), which uses the concept of Artiﬁcial Po-

tential Field, is adopted as the starting point. Thus,

Section 2 describes this obstacle avoidance method

and presents a simulated example using it. In the se-

quence, Section 3 describes a modiﬁcation here pro-

posed to the impedance based control and presents a

simulated example using the new strategy for avoid-

ing obstacles. Next, Section 4 presents two experi-

ments using the new strategy here proposed to avoid

obstacles. Finally, Section 5 highlights the main con-

clusions.

The simulations presented in Section 2 and Sec-

341

Ferreira A., Sarcinelli Filho M. and Freire Bastos Filho T. (2005).

A NEW APPROACH TO AVOID OBSTACLES IN MOBILE ROBOT NAVIGATION: TANGENTIAL ESCAPE.

In Proceedings of the Second Inter national Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 341-346

DOI: 10.5220/0001169403410346

 SciTePress

tion 3 were accomplished using the simulator that

accompanies the Pioneer 2-DX mobile robot, while

the experimental results were obtained using the Pio-

neer 2-DX itself, with an onboard computer based in

the Intel Pentium MMX 266 MHz processor having

128 MBytes of RAM and running the Linux operating

system. The sensors used are 16 ultrasonic sensors in

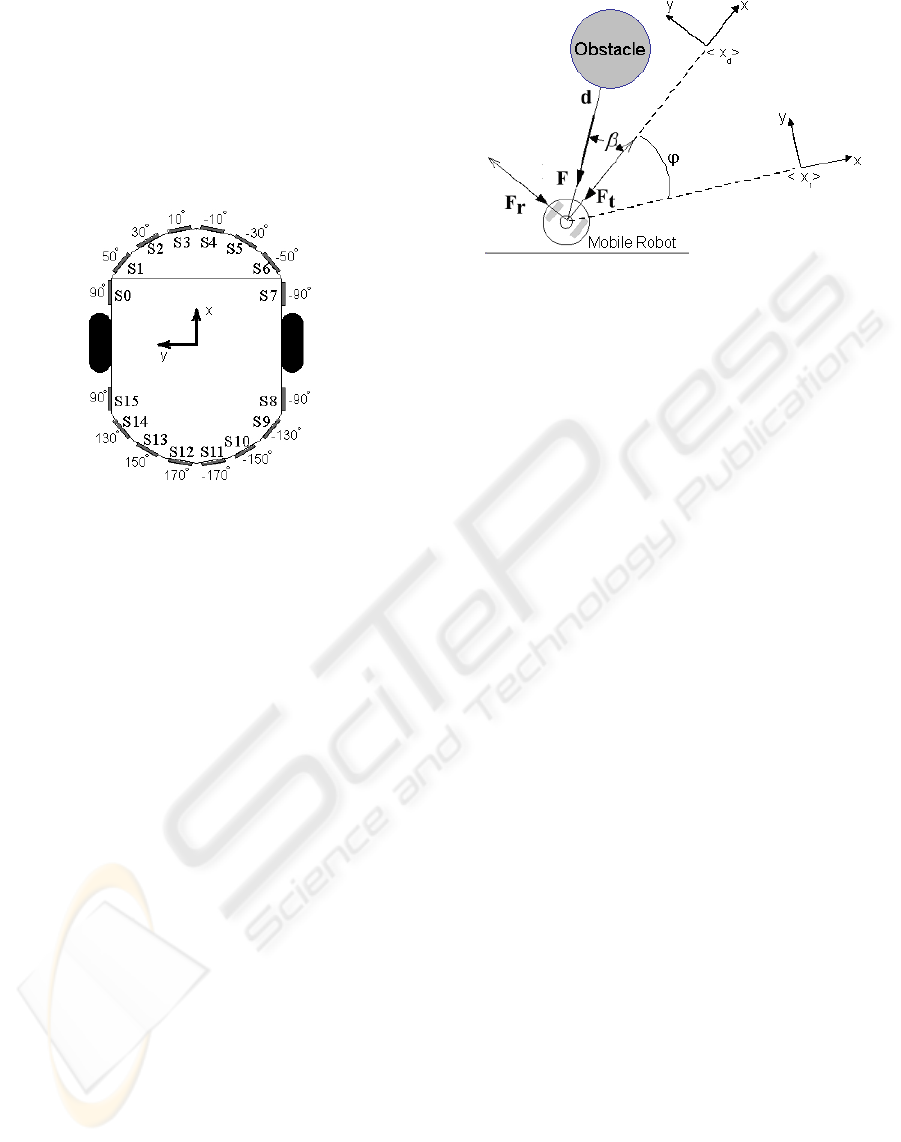
a ring distributed like depicted in Fig. 1.

Figure 1: Sonar distribution for the Pioneer 2-DX platform.

2 THE IMPEDANCE-BASED

CONTROL SYSTEM

This control system uses the concept of generalized

or extended impedance to represent the relationship

between the robot movement and a ﬁctitious repul-

sive force (Hogan, 1985; Secchi et al., 2001). Such

a repulsive force is a function of the distance robot-

obstacle. A contact robot-obstacle should be avoided,

what is accomplished by generating a repulsive force

that increases when the robot gets closer to the obsta-

cle.

2.1 Describing the Impedance Based

Control System

Fig. 2 shows a situation in which an obstacle is de-

tected by the robot sensors. The repulsive force F is

generated, causing a temporary displacement of the

goal point x

, which allows the robot to avoid the ob-

stacle by changing its heading angle. The components

of the force F — F

(the component coinciding with

the robot orientation) and F

(the component normal

to the robot orientation) — are also represented.

The magnitude of the repulsive force F the obsta-

cle exerts on the robot is calculated as (Secchi et al.,

2001)

F = a − b[d − d

min

]

, (1)

Figure 2: The ﬁctitious force generated by an obstacle.

where a and b are positive constants related by a =

b[d

max

− d

min

]

, d

min

is the minimum distance the

sensors are able to measure, d

max

is the maximum

distance intended to cause a nonzero ﬁctitious repul-

sive force and d is the smallest robot-obstacle distance

currently measured by the robot sensors. Notice that

min

< d < d

max

, and d

max

characterizes the re-

pulsion zone, deﬁned as the region inside which the

ﬁctitious repulsive force has a non-zero value.

An impedance Z(s) is then deﬁned as

Z(s) = Bs + K, (2)

where B and K are positive constants representing

the damping and spring effect of the interaction robot-

obstacle in the repulsion zone, respectively. The im-

pedance error x

is calculated using the component

(Fig. 2), as

= Z(s)

−1

, (3)

while the angle ϕ that causes a rotation in the target

position x

is given by

ϕ = x

sign(F

). (4)

Thus, the real target position x

is rotated to a tem-

porary position x

given by

cos ϕ sin ϕ 0

− sin ϕ cos ϕ 0

0 0 1

, (5)

which becomes the new reference to the ﬁnal pose

controller (a control loop responsible for taking the

robot to the goal), as shown in Fig. 3. There the con-

trol signals u and ω represent the robot linear and an-

gular velocities, respectively, while the current pose

of the robot, in cartesian coordinates, is characterized

by x

′

= [x

Whenever an obstacle is detected in the repulsion

zone, a ﬁctitious force F is generated, which gener-

ates a non-zero rotation angle ϕ, causing the robot to

avoid the obstacle (the external loop, relative to the

ICINCO 2005 - ROBOTICS AND AUTOMATION

342

Figure 3: Block diagram corresponding to the Impedance Based Control System.

impedance controller (Hogan, 1985)). The rotation

(avoidance) angle is inversely proportional to the dis-

tance robot-obstacle and to the angle β. In this strat-

egy the path the robot takes to escape from an obstacle

is not taken into account. The vehicle is supposed to

get close to the real target position while maneuver-

ing to avoid any obstacle. After passing the obstacle,

the angle ϕ becomes zero and the rotation matrix be-

comes an identity one, thus causing x

not to change.

Finally, it is worthy to emphasize that this control

system is stable in the Lyapunov sense (Secchi et al.,

2001). This means that the robot will always reach

the goal (if the goal is reachable), independently of

the obstacles in its path.

2.2 A Simulated Example

An example is here simulated, in which the ro-

bot should reach the point (9000 mm, 5000 mm),

avoiding any obstacle in its path. Fig. 4 shows the

path followed by the robot from the starting point

(0 mm, 0 mm, 0) to the destination point (the orien-

tation of the robot when reaching the goal is not taken

into account). When an obstacle is detected, a ﬁcti-

tious force is generated and the robot makes a turn.

The value of d

max

was chosen to be 70 cm. Fig. 5

shows the control signal u generated by the ﬁnal pose

controller. From such ﬁgure one can notice meaning-

ful variations in the robot linear velocity. They mean

great acceleration and deceleration of the robot mo-

tors.

3 THE NEW CONTROL SYSTEM

A new control system is here proposed, which is

based in escape paths that are tangent to the obstacle

detected. Such a control system uses just part of the

Impedance Based Control system, namely the inner

loop in Fig. 3 (see Fig. 6). The difference is that the

rotation angle ϕ is not calculated using the repulsive

force F anymore, but using the angular position of

the obstacle relative to the robot. The rotation angle

is now determined to make the vehicle to turn around

Figure 4: The path followed by the robot (Impedance).

0 5 10 15 20 25 30 35 40 45 50

−50

100

150

200

250

300

350

t [s]

u [mm/s]

Figure 5: The linear velocity of the robot (Impedance).

until getting aligned to the tangent to the obstacle con-

tour. One advantage of this method is that the robot

contours the obstacle, thus describing excellent trajec-

tories when navigating (Maravall and de Lope, 2002),

as it is shown in the sequence.

A NEW APPROACH TO AVOID OBSTACLES IN MOBILE ROBOT NAVIGATION: TANGENTIAL ESCAPE

343

Figure 6: Block diagram corresponding to the new control system.

3.1 Describing the New Control

System

When the robot gets into the repulsion zone (Fig. 7),

the angle β is determined (it is the angle between the

axis of movement of the robot and the radius corre-

sponding to the sensor measuring the least distance

from the robot to the obstacle detected). Knowing the

robot orientation relative to the real target (the angle

α) and the positions of the ultrasonic sensors around

the robot platform, the angle ϕ that allows a tangential

deviation is obtained as

ϕ =



− |β|



reverseSign(β) − α, (6)

where reverseSign(β) corresponds to −Sign(β).

Figure 7: Obtaining the angle ϕ.

The angle ϕ is then used in the rotation matrix in

(5) and the real target is rotated to a new position (the

virtual target). The ﬁnal pose controller, which calcu-

lates the new robot orientation to reach the target, uses

the coordinates of the virtual target, causing the robot

to take the tangent to the obstacle border. Notice that

in the absence of obstacles the change in the position

of the real target is null, and the robot continues seek-

ing for the real target. This algorithm is represented

in Fig. 6, where u, ω and the vector x

have the same

meaning as in Section 2.

It is important to notice that the control loop cor-

responding to the proposed controller is slower than

the control loop corresponding to the ﬁnal pose con-

troller. Then, the robot is able to follow the varia-

tion imposed to the target position. Notice also that

the same idea applies to the impedance based con-

trol. Knowing this, the asymptotic stability of the

impedance based control system is demonstrated in

(Secchi et al., 2001). Now, if one compares the block

diagrams corresponding to both impedance based and

tangential deviation control systems, it is possible to

realize that the proposed control system is also as-

ymptotically stable, once the inner loop of both sys-

tems is the same. This means that the strategy here

proposed for obstacle deviation always takes the ro-

bot to the target (if the target is reachable), thanks to

its asymptotic stability.

3.2 A Simulated Example

The objective in this simulation is to take the robot

from the starting point (0 mm, 0 mm, 0) to the goal

point (9000 mm, 5000 mm) once more, avoiding any

obstacle in its path. Fig. 8 shows the path the robot

followed until reaching the goal. As the obstacles (the

walls of the corridors the robot enters in) are detected,

the robot turns around in order to follow a line paral-

lel to the walls. The repulsion zone was deﬁned as

70 cm once more. Fig. 9 shows the linear velocity

developed by the robot. An important remark about

this method is that while avoiding obstacles, approxi-

mately between 4s and 17s in Fig. 9, the robot keeps

navigating with constant linear velocity (the values of

the angular velocity and the orientation, in such time

interval, are very close to zero).

3.3 Comparing the Results

After analyzing the graphics related to the impedance

based control system and the proposed control sys-

tem, it is possible to ﬁgure out some strong differ-

ences between both approaches. The ﬁrst one is

that while avoiding obstacles the strategy here pro-

posed assures constant linear velocity to the robot,

thus avoiding unnecessary acceleration and deceler-

ation, reducing the energy consumption and saving

batteries.

In addition, the tangential obstacle avoidance al-

lows reaching the target point in less time than the

ICINCO 2005 - ROBOTICS AND AUTOMATION

344

Figure 8: The path followed by the robot (Proposed

Method).

0 5 10 15 20 25 30 35 40 45 50

−50

100

150

200

250

300

350

t [s]

u [mm/s]

Figure 9: The linear velocity of the robot (Proposed

Method).

impedance based strategy. This is a consequence of

the facts that the path the robot follows is closer to

the optimum one, as one can see in Fig. 8, and the ro-

bot linear velocity is not decreased during the obstacle

avoidance, which occurs when using the impedance

based strategy. Therefore, the strategy here proposed

for obstacle avoidance is extremely attractive.

In addition, the simulated example itself shows that

the tangential strategy for obstacle avoidance gives

the robot the capability of following walls or corri-

dors with no additional computation.

4 EXPERIMENTAL RESULTS

In order to validate the control system here proposed,

it was programmed in the computer onboard the Pi-

oneer 2-DX mobile robot and was tested in various

experiments. One of these experiments corresponds

to the trajectory in Fig. 10, and conﬁrms the ef-

fectiveness of the tangential obstacle avoidance ap-

proach. The robot is supposed to reach the point

(9000 mm, 5000 mm), starting navigating in the

point (0 mm, 0 mm, 0). This experiment conﬁrms

the simulated results, as one can see by comparing the

graphics corresponding to the real experiment and to

the simulation in Section 3.

The second experiment corresponds to a very im-

portant situation (see Fig. 11): due to the position of

of the starting point and the goal, as well as the conﬁg-

uration of the walls, the robot is supposed to describe

an U path. In this situation it is forced to overlap the

goal position, because of the wall at its left side, thus

going too far from the goal before restarting seeking

for it again. This point represents a local minimum

and the proposed method allows escaping from situ-

ations like that, as shown in the experiment. As one

can see, it does not gets stuck in a local minimum, like

it happens in connection to the Potential Field method

(and those that are derived from it). The same ﬁgure

also shows how the robot performs when there are ob-

stacles in a corridor: the tangential escape approach

makes it to contour the obstacle, like one can see in

Fig. 11.

Figure 10: The path followed by the robot (Proposed

Method).

As one can also see from Fig. 11, the approach pro-

posed to avoid obstacles has been successful in guid-

ing the robot through narrow passages. The two ob-

stacles in the ﬁrst horizontal and in the vertical cor-

ridors create narrow passages through which the pro-

posed control system guides the robot.

To close the experimentation, the same experi-

ments were also run using the Impedance Based Con-

trol system. In the ﬁrst one the robot reached the goal

without major problems, but in the second one it did

not manage to go beyond the obstacle in the horizon-

tal corridor. Then, one gets the conclusion that the

proposed approach is effectively much better in terms

of avoiding obstacles, energy consumption, time to

get the goal and motor wearing.

A NEW APPROACH TO AVOID OBSTACLES IN MOBILE ROBOT NAVIGATION: TANGENTIAL ESCAPE

345

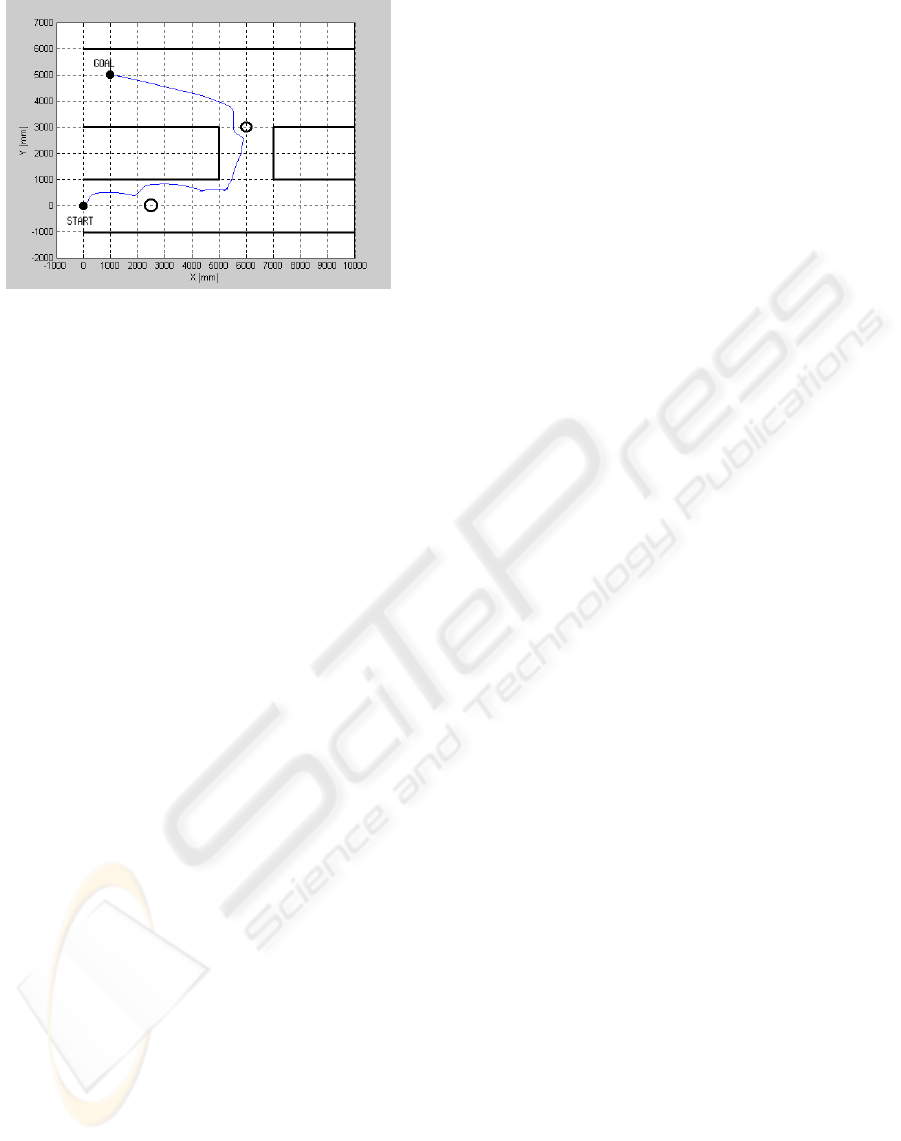
Figure 11: Experiment in a U-path with two obstacles (Pro-

posed Method).

5 CONCLUSION

A new method is proposed in this paper to control a

mobile robot when avoiding obstacles along its path

from a starting point to a target point. Such method

is a modiﬁcation of the well known Impedance Based

Control System, in which the target point has its real

position temporarily redeﬁned, thus causing a change

in the robot path in order to deviate from any obsta-

cle. The same strategy is here adopted, but the idea is

to redeﬁne the temporary position of the target point

according to a new paradigm: the robot should keep

aligned to the tangent to the obstacle border.

The control system thus implemented is shown

to be stable in the Lyapunov sense, as well as the

impedance based one, and many experiments have

shown its efﬁciency in guiding the robot. The whole

path followed by the robot is quite close to the optimal

one, the maneuvers performed are softer, the naviga-

tion time is lower and the motors of the mobile robot

are less demanded, for the lower variations imposed to

the angular and linear velocities, as it can be checked

in the experiments presented.

Finally, besides its simplicity and effectiveness, it

should be emphasized that the proposed control sys-

tem also allows implementing the behaviors Wall Fol-

lowing and Corridor Following with no additional

computation.

REFERENCES

Althaus, P. and Christensen, H. I. (2002). Behaviour co-

ordination for navigation in ofﬁce environments. In

IEEE/RSJ International Conference on Intelligent Ro-

bots and System, volume 3, pages 2298–2304, Lau-

sanne, Switzerland.

Borenstein, J. and Koren, Y. (1989). Real-time obstacle

avoidance for fast mobile robots. IEEE Transactions

on Systems, Man, and Cybernetics, 19(5):1179–1187.

Borenstein, J. and Koren, Y. (1991). The vector ﬁeld

histogram - fast obstacle avoidance for mobile ro-

bots. IEEE Transactions on Robotics and Automation,

7(3):278–288.

Brock, O. and Khatib, O. (1999). High-speed navigation us-

ing the global dynamic window approach. In Proc. of

the 1999 IEEE International Conference on Robotics

and Automation, volume 1, pages 341–346.

Elfes, A. (1987). Sonar-based real-world mapping and nav-

igation. IEEE Journal of Robotics and Automation,

RA-3(3):249–265.

Fox, D., Burgard, W., and Thrun, S. (1997). The dynamic

window approach to collision avoidance. Robotics &

Automation Magazine, IEEE, 4(1):23–33.

Hogan, N. (1985). Impedance control: An approach to ma-

nipulation. ASME Journal of Dynamic Systems, Mea-

surement, and Control, 107:1–23.

Khatib, O. (1986). Real time obstacle avoidance for manip-

ulators and mobile robots. The International Journal

of Robotics Research, 5(1):90–98.

Kuc, R. and Barshan, B. (1989). Navigating vehicles

through an unstructured environment with sonar. In

Proc. of the 1989 IEEE International Conference on

Robotics and Automation, volume 3, pages 1422–

1426, Scottsdale, AZ.

Maravall, D. and de Lope, J. (2002). Integration of arti-

ﬁcial potential ﬁeld theory and sensory-based search

in autonomous navigation. In XV World Congress

of the International Federation of Automatic Control,

IFAC’2002, Barcelona, Spain.

Minguez, J. and Montano, L. (2004). Nearness diagram

(nd) navigation: collision avoidance in troublesome

scenarios. IEEE Transactions on Robotics and Au-

tomation, 20(1):45–59.

Secchi, H., Carelli, R., and Mut, V. (2001). Discrete sta-

ble control of mobile robots with obstacles avoidance.

In International Conference on Advanced Robotics,

ICAR’01, pages 405–411, Budapest, Hungary.

ICINCO 2005 - ROBOTICS AND AUTOMATION

346