
MULTIPLE VIEW GEOMETRY ESTIMATION BASED ON
FINITE-MULTIPLE EVOLUTIONARY AGENTS FOR MEDICAL
IMAGES
Mingxing Hu, Karen McMenemy, Stuart Ferguson, Gordon Dodds
Virtual Engineering Centre, Queen’s University Belfast, Malone Road, Belfast, United Kingdom
Baozong Yuan
Institute of Information Science, Beijing Jiaotong University, Beijing, P. R. China
Keywords: Trifocal tensor, evolutionary agent, survival-of-f
inite-fittest, trilinear constraint, robust estimation.
Abstract:
In this paper we present a new method for the robust estimation of the trifocal tensor, from a
series of medical images, using finite-multiple evolutionary agents. Each agent denotes a subset
of matching points for parameter estimation, and the dataset of correspondences is considered as
the environment in which the agents inhabit, evolve and execute some evolutionary behavior.
Survival-of-finite-fitness rule is employed to keep the dramatic increase of new agents within
limits, and reduce the chance of reproducing unfit ones. Experiments show that our approach
performs better than the typical methods in terms of accuracy and speed, and is robust to noise
and outliers even when a large number of outliers are involved.
1 INTRODUCTION
Within recent years advances in the field of digital
imaging have played a key role in medical industry.
Medical imaging has progressed significantly
throughout the years from X-Ray, CAT and PET
scans to now using endoscopic cameras. Three-
dimensional reconstruction methods are central to
many new applications to medical imaging. In this
research, we wish to generate 3D views of an
endoscopic procedure, via a head up display unit, in
order to enhance features, in particular obscured
features, to the surgeon. However, the generation
of exact 3D models from uncalibrated endoscopic
camera image sequences is a challenging problem.
To generate these three dimensional views we
need to know
accurately the geometric information
of the endoscopic camera. The trifocal tensor is the
geometric entity that relates 3D points to three 2D
views. In order to determine the trifocal tensor, for
exact 3D reconstruction, we must extract interest
points from the three images using the corner
detector and then match potential features between
these images.
In the past years, accurate and robust estimation
of
trifocal tensor has become an important and
productive research area. The well-known robust
methods are RANSAC (Random Sample Consensus
Paradigm) (Torr, 1995), and its improvement
MLESAC (Maximum Likelihood Sample
Consensus) (Torr, 1997). Both methods randomly
sample a subset of correspondences for geometric
parameter estimation. However, the MLESAC
method also employs additional statistical measures
for the final solution. Both methods can deal with
image noise and outliers, which are in gross
disagreement with a specific postulated model.
However, when a large number of outliers are
involved they perform poorly.
Messy genetic algorithm (MGA) has also been
u
sed for trifocal tensor estimation (Hu, 2002). This
method uses genes to denote triplets of
correspondences and employs a genetic mechanism
to improve the effectiveness of outlier detection.
However, this method does not exploit the intrinsic
parallelism between corresponding images and is
therefore computational intensive. This is a defect
of nearly all GA-based applications.
Recently, the authors proposed a simple
evol
utionary agent-based approach (SEA) to the
problem of trifocal tensor estimation (Hu, 2004).
This was found to improve the robustness of
parameter estimation and reduce the computational
202
Hu M., McMenemy K., Ferguson S., Dodds G. and Yuan B. (2005).
MULTIPLE VIEW GEOMETRY ESTIMATION BASED ON FINITE-MULTIPLE EVOLUTIONARY AGENTS FOR MEDICAL IMAGES.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 202-209
DOI: 10.5220/0001169802020209
Copyright
c
SciTePress

expense. However, through experimentation it was
found that the simplicity of evolutionary operators
caused the number of new generated agents to
increase almost exponentially at early stages.
Moreover, if there is no rule about termination, the
method will spend a long time on convergence.
In this paper we present a new method for robust
estimation of the trifocal tensor, from a series of
medical images, using finite multiple evolutionary
agents (FMEA). The dataset of correspondences is
viewed as a one-dimensional cellular environment in
which the agents inhabit and evolve. Each agent
represents a subset for computing a unique trifocal
tensor, and will execute some evolutionary behavior
e.g. reproduction and diffusion. In this new method,
the survival-of-finite-fitness rule is introduced to
limit the increase of new agents. During the
diffusion process, after the comparison with their
parents, the successful agents are sorted by their
costs, and the best set of agents is kept active for
evolutionary processing. Experiments show that the
new FMEA approach performs better than the
original SEA approach in terms of accuracy and
robustness. This scheme provides a richer population
with better agents and more exploration to avoid
unfavorable local minima than SEA, and decreasing
the computation expense greatly.
The organization of the paper is as follows. In
section 2, we give a brief introduction to multiple
view geometry estimation. Then a new approach
based on evolutionary agents is presented in detail,
including agent definition, cost function and
evolutionary behavior. Section 4 deals with the
experimental results obtained from synthetic data
and real images. Finally, the conclusions are drawn
in section 5.
2 BACKGROUND OF MULTIPLE
VIEW GEOMETRY
ESTIMATION
Consider a single point
M
in space projected onto
views with camera matrices
P
, ,
3
P
′
P
′
′
with
image points
m
, ,
m
′
m
′
′
respectively. Note that
for some scalar . Consider
and
T
yx ) ,1 , ,(
λ
=M
λ
]|[ 0IP = ] |[ vAP
′
=
′
where is the
principle minor of
P
and is the fourth column of
. Consider and eliminate the scale
factor:
A
33×
′
v
′
P
′
MPm
′
≅
′
33
11
3
va
vma
a
a
′
+
′
+
==
′
λ
λ
xx
x
x
T
T
T
T
i
33
22
3
2
va
vma
a
a
′
+
′
+
==
′
λ
λ
xx
x
y
T
T
T
T
where
is the
i
th row of . These two equations
can be written more compactly as follows:
i
a
A
0=
′
+
′′
Amsvs
TT
λ
0=
′′
+
′′′
Amsvs
TT
λ
where
) ,0 ,1( x
′
−
=
′
s and . Yet in a
more compact form consider
s
, as row vectors
of the matrix
) ,1 ,0( y
′
−=
′′
s
′
s
′′
]
10
01
[
y
x
j
′
−
′
−
=
µ
s
where
3 ,2 ,1
=
j and 2 ,1
=
µ
. Therefore, the compact
form we obtain is described as follows:
0=+
′
j
ij
ij
j
asmvs
µµ
λ
(1)
where
µ
is a free index (i.e., we obtain one equation
per range of
µ
). Similarly, let for the
third view
]|[ vBP
′′
=
′′
MPm
′
′
≅
′
′
and let be the matrix,
ρ
k
r
]
10
01
[
y
x
k
′′
−
′′
−
=
ρ
r
And likewise,
0=+
′′
k
ik
ik
k
brvr
ρρ
πλ
(2)
where
2 ,1
=
ρ
is a free index. We can eliminate
λ
from (1) and (2) and obtain a new equation:
0)( =
′′
−
′
j
i
kk
i
j
kj
i
p avbvrs
ρµ
and the term in parenthesis is a trivalent tensor we
call the trilinear tensor:
j
i
kk
i
jjk
i
avbvT
′′
−
′
= (3)
Hence, we have four trilinear equations (note that
2 ,1,
=
ρ
µ
). In a more explicit form, these
trilinearities look like:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=−
′
+
′′′
−
′′
=−
′
+
′′′
−
′′
=−
′
+
′′′
−
′′
=−
′
+
′′′
−
′′
0
0
0
0
22323323
21313323
12323313
11313313
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
ppypyypy
pypyxpx
ppxpxypy
ppxpxxpx
TTTT
TpTTT
TTTT
TTTT
(4)
Equation (4) was first introduced by Shashua in
1995, from where we can see that the trifocal tensor
has 27 elements, but only their ratios are significant,
leaving 26 coefficients to be specified. And each
triplet of matching points can provide four
independent linear equations for the elements of the
tensor. Therefore the tensor can be computed from a
minimum of 7 triplets using Least-Squares methods.
MULTIPLE VIEW GEOMETRY ESTIMATION BASED ON FINITE-MULTIPLE EVOLUTIONARY AGENTS FOR
MEDICAL IMAGES
203

), ,(
111
mmm
′′′
1
V
7
V
2
V
), ,(
222
mmm
′′′
), ,(
1111 −−−
′′′
nnn
mmm
), ,(
nnn
mmm
′′′
Figure 1: Agent representation
3 MULTIPLE VIEW GEOMETRY
ESTIMATION WITH FINITE
MULTIPLE EVOLUTIONARY
AGENTS
According to the description above, ideally every
possible sub-sample (seven correspondences) of all
the matching points
n should be considered to
obtain the optimal result. However this is usually
computationally infeasible for most applications. So
we apply finite multiple evolutionary agents to
explore large uncertainty-parameter space and avoid
getting trapped at a local minimum.
3.1 Agent definition
Suppose that
S
is the dataset of correspondences
iii
. It may be viewed as a
one-dimensional grid of triplets of matching points,
and also as an environment in which the agents
inhabit and evolve. The goal of the evolutionary
agents in
S
is to select the potential good points and
search the preferred optimal subset. The
evolutionary agent is defined as follows
(){
n
}
, ,1 | , , L=
′′′
mmm i
DieDiffRepfmlDaAgent
t
, , , , , ,
cos
V=
V
denotes the positions of an agent in
S
, a
seven-dimensional position vector, and
k
, , is just the index
number of correspondence lattice
S
, as shown in
Figure 1. In other words,
V
stands for the subset of
correspondences for geometry estimation. denotes
the age of an agent, that is, the number of diffusion
steps it has taken;
t
D
cos
symbolizes its cost, which
indicates the adaptability of an agent and can be
computed using the trilinear constraint obtained
from the correspondences of
V
; represents the
family index, which indicates where an agent comes
from.
Rep denotes the reproduction behavior;
represents the diffusion behavior; while
Die
indicates that an agent has a life span.
{}
niiV , ,1 | L==
7 , ,1 L=k
a
fml
Diff
3.2 Cost function
In this paper, we employ the seven-point method to
get one possible solution of the tensor, although it
could be estimated by six-point method (Quan,
1994). The reasons are as follows. Seven-point
method is a simple linear approach, while six-point
method is much complicated which includes
parameterization of matrices, solving cubic
constraint and linear equations. Moreover, the
advantage of agent-based algorithm is that each
agent performs a simple task, but they work together
to solve a problem of great complexity by
communicating and cooperating with each other. So
the trade-off between accuracy and speed is to
choose the seven-point method, which does not put a
heavy burden on agents.
In order to compare the results of geometry
estimation obtained from agents, the cost function is
defined based on the residuals of correspondences
()()()
∑∑
==
′′′′
+
′′
+==
n
i
iiiiii
n
i
i
dddRR
1
222
1
ˆ
ˆ
ˆ
m,mm,mm,m
i.e., the sum of squared geometric distances between
the measurements
,
i
m
i
m
′
, and the corrected
data points
, , , the latter obeying the
trilinear constraint (3) for the estimated tensor
.
It indicates the distinction between the noisy
measurements and the geometric elements (the true
or equivalently the corrected data points). Then the
cost function of an agent is defined by
i
m
′′
i
m
ˆ
i
m
ˆ
′
i
m
ˆ
′′
jk
i
T
(
∑∑
==
−+=
n
i
i
n
i
iit
RD
11
cos
1
ωβω
)
(5)
where
i
ω
satisfies the following equation
⎩
⎨
⎧
≤
=
)( 0
)( 1
outlierotherwise
inlierRif
i
i
β
ω
σ
β
96.1
=
is the threshold for considering the
inliers, and the standard deviation
σ
can be found
as a maximum likelihood estimate using the median
ICINCO 2005 - ROBOTICS AND AUTOMATION
204

)(
)1(
g
α
)1(
)1,1(
+g
α
)1(
),1(
+g
m
br
α
)(
)(
g
•
α
A
)(
)(
g
i
α
)1(
),(
+
•
g
i
α
)(
)(
g
i
age
)(
)(
g
i
α
best
n
)(
)(
g
n
best
α
)1(
)1,(
+g
n
best
α
)1(
),(
+g
mn
brbest
α
Figure 2: The evolutionary process of Finite Multiple Evolutionary Agent
ii
Rmed
qn
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+=
5
14828.1
σ
, where
q
is the
number of parameters. It can be seen that outliers are
given a fixed penalty, but inliers are scored on how
well they fit the data. In other words, the main
consideration is given to the residuals of inliers and
the outliers make a little contribution to the cost
function.
3.3 Evolutionary behavior
Evolutionary agents adapt to their environment
mainly by way of two behavioral responses, namely,
reproduction and diffusion. Letting
)( g
A
represent the
set of all active agents in generation
g
, the
evolutionary process is detailed in Figure 2.
(1) Reproduction: In the reproduction process,
each active agent
will breed a finite number
br
of offspring agents. The larger the value of
br
,
the more offspring agents will be created to search in
the large uncertain parameter space. However the
computational cost will increase dramatically if no
parallel processing is applied. It should be pointed
out that the offspring,
, are by no means a
simple copy of the parent
. The differences
between
and are mainly in the position
vectors
and .
ch
elements of are
selected and changed into the index number of
by
a random number generator. In other words,
may be viewed as the mutation of his parent
,
and new values, randomly selected numbers in
S
,
are introduced to
. Therefore the subset of the
offspring for computing the tensor
is partly
changed.
)( g
α
m m
)1( +g
α
)( g
α
)( g
α
)1( +g
α
)( g
V
)1( +g
V
m
)( g
V
S
)1( +g
α
)( g
α
)1( +g
V
jk
i
T
We should emphasize that after the reproduction
process, the position vector of each agent should be
checked to ensure the elements are different from
each other. If the same value is found, it will be
replaced by a randomly generated one.
(2) Diffusion: The diffusion behavior plays an
important role for an agent to search new positions
in the correspondence lattice. After the reproduction
process, each agent of generation
()
, ,
computes the cost using Eq. (5), and compares it
with that of its parent
. If the offspring has the
cost advantage, it will survive and be appended to
the active agent set
1+g
)1( +g
α
)( g
α
A
. Its parent, however, will
become inactive and be removed from the
environment. If has a worse performance than
its parent, it will be deleted at once without any
chance to search further in the space. If the offspring
of the same parent are all failed, their parent
will be kept active in the environment with its age
increased by one. Then all the successful agents in
data set
)1( +g
α
)1( +g
α
A
are sorted ascendingly according to their
cost, and the first
best
agents are kept active with the
removing of the others from the environment, which
n
MULTIPLE VIEW GEOMETRY ESTIMATION BASED ON FINITE-MULTIPLE EVOLUTIONARY AGENTS FOR
MEDICAL IMAGES
205

Figure 3: The algorithm for evolutionary agent-based computation
Input: A 1 grid of correspondencesn×
Output: trifocal tensor
begin
distribute an initial set of agents
{
}
)0(
α
in the environment,
assign the elements of position vector
to the index of V S
in numerical order (
1 ), , n , ,3 ,2 , L
0)(
)0(
←
α
age
assign the initial agent set to the currently-active agent set:
{
}
)0(
α
←A ,
compute the cost of agents in the initial set
select the subset template from the agents in
{
}
)0(
α
while
φ
≠A do
reproduction process, select element
V ,
k
V
or
V
,
][Templaterandom
k
diffusion process,
←
k
← ][nrandom
vanishing process,
update subset template,
endwhile
compute tensor using the position vector of the best agent,
return trifocal tensor,
end
could also be called the survival-of-finite-fittest. If
the number of successful agents is less than
best
,number of active agents, and ends with the
same numb then keep all the remaining active. Thus
each evolutionary generation will begin with finite
er of, or fewer offspring of better quality.
n
3.4 Subset template
In order to improve the collaborative ability of the
agents, we apply a subset template in the
evolutionary process. The subset template is the
position vector of the best agent from each
generation. In the next generation, the agents will
select some elements from the template for
reproduction by probability
T
, which have a higher
possibility to be good matching points. Thus the
reproduction behavior of the evolutionary agent has
to be partly revised: two elements of
are
selected and changed into: (1) an element from the
subset template with probability
T
P , or (2) a
random index number of
S with probability
T
P
)( g
V
P
−
1 .
The larger
T
P is, the more entries will be chosen
from the template, but the fewer new positions will
appear in the offspring, which affects the explorative
ability of the agents in some way.
We would also emphasize that after each
generation we will check the ages of active agents. If
the age of an agent exceeds its life span, it will be
removed from the environment, which avoids
useless computation. If there is no active agent in the
evolutionary environment, the whole process halts.
4 EXPERIMENTAL RESULTS
In this part, our novel approach is compared with
several typical methods including RANSAC,
MLESAC, MGA and SEA. In order to analyze the
effectiveness of subset template, we use SEA+T and
FMEA+T to denote the methods with templates, this
discriminating them from SEA and FMEA methods.
4.1 Experiments with synthetic data
In the experiments with synthetic data, the
correspondences are randomly generated by space
points in the region of
visible to three different
positions of a synthetic camera:
3
ℜ
]0C[IP =
(
C stands for camera intrinsic matrix),
[
]
tRCP
′′
=
′
and
[
]
tRCP
′′′′
=
′′
, where the camera makes
rotations
R
′
and R
′
′
, and translations and t
′
t
′
′
.
Here the total number of correspondences is 100,
and there are only 10 agents in
{
}
)0(
α
. The number
of agents for initialization may be larger than 10, but
it will take more time for computation and ten agents
has been found in practice to be good enough for
real applications. The experiments are divided into
two groups:
(G1): Six different ranges of Gaussian noise are
added to the projective correspondences, whose
means are 0 and standard deviation vary from 0.5 to
3.0 (in steps of 0.5), as shown in Table 1.
ICINCO 2005 - ROBOTICS AND AUTOMATION
206

Table 1: Residual error under variable variance of noise
Method
Noise level
RANSAC MLESAC MGA SEA SEA+T FMEA FMEA+T
0.5 1.174 0.865 0.782 0.852 0.824 0.817 0.803
1.0 2.194 1.389 1.197 1.224 1.185 1.225 1.209
1.5 3.253 1.546 1.367 1.563 1.489 1.460 1.442
2.0 4.438 1.790 1.572 1.763 1.712 1.657 1.646
2.5 5.906 1.923 1.763 1.942 1.825 1.815 1.793
3.0 7.234 2.341 1.914 2.242 2.026 1.988 1.942
(a) (b)
Figure 4: Residual error under noise-perturbation test, (a) results of all the seven methods, (b) results of genetic algorithm
and EA-based approaches.
(a) (b)
Figure 5: Residual error under outlier-perturbation test, (a) results of all the seven methods, (b) results of genetic algorithm
and EA-based approaches.
Table 2: Residual error under different percentage of outliers
Method
Outlier
percentage
RANSAC MLESAC MGA SEA SEA+T FMEA FMEA+T
10% 3.734 1.426 1.253 1.286 1.237 1.232 1.231
20% 4.925 1.532 1.314 1.421 1.395 1.310 1.320
30% 10.83 1.973 1.724 1.895 1.827 1.755 1.710
40% 15.72 2.272 1.978 2.263 2.211 2.116 2.018
50% 34.86 2.925 2.226 2.485 2.406 2.421 2.332
MULTIPLE VIEW GEOMETRY ESTIMATION BASED ON FINITE-MULTIPLE EVOLUTIONARY AGENTS FOR
MEDICAL IMAGES
207

Table 3: Average computation time for two groups (Sec.)
Method
Group
RANSAC MLESAC MGA SEA SEA+T FMEA FMEA+T
G1 3.141 2.735 4.320 2.324 2.418 1.563 1.615
G2 3.673 3.573 4.456 2.141 2.152 1.325 1.377
Figure 6: Computation time of synthetic data test
(G2): The means and standard deviation of
Gaussian noise are fixed to 0, 1, respectively; the
percentage of outliers disturbed by the noise and
false matches are varied from 10% to 50%, as shown
in Table 2.
Tables 1 and 2 show the experimental results of
(G1) and (G2) respectively, and Figures 4 and 5 also
illustrate them. Table 3 shows the average
computation time taken by these methods, which is
also illustrated in Figure 6. From these tables and
figures, it can be noticed that the EA-based
approaches perform better than other typical
methods, and almost as well as genetic algorithm in
terms of accuracy. In the four EA-based methods,
FMEA turns out to be the quickest followed by
FMEA+T. The residual error of FMEA is smaller
than that of SEA, and the computation time
decreased by 48.69% in the noise-perturbation test,
and 61.58% in the outlier-perturbation test. This
strongly suggests that the survival-of-finite-fitness
rule efficiently relieves the computational burden by
removing a large number of unfit agents. It can also
be seen that FMEA +T and SEA+T obtain better
results than FMEA and SEA, which confirms that
the subset template improves the communication
among all the agents in the population and helps
offspring inherit good resources.
4.2 Experiments with medical
images
The performance of our approach is also
demonstrated by using a variety of image triplets.
Three different triplets of medical images are taken
from a laparoscopic operation. Figure 7 illustrates
the first triplet of images we utilized. The white
circles denote the feature points obtained with corner
detector, and the white arrow lines illustrate the
movement of matching points between the images.
Table 4 shows the residual error of the medical
image testing. We can see that FMEA method also
perform best in real image experiments. The mean
residual error of RANSAC, MLESAC, MGA and
SEA are7.240, 1.132, 0.886 and 1.070 times as
much as that of FMEA. As to the computational
efficiency, FMEA works so fast that the
computation time for FMEA is 0.4158, 0.6832 as
much as those of SEA and MGA, respectively.
From the experiments it can be concluded that
the novel evolutionary strategy of FMEA helps
agents search for a fit parameter set in the uncertain
solution space, and allows them to move more
efficiently toward the global optimum by gradually
reducing the chance of reproducing an unfit dataset.
Figure 7: The medical images from three viewpoints
ICINCO 2005 - ROBOTICS AND AUTOMATION
208
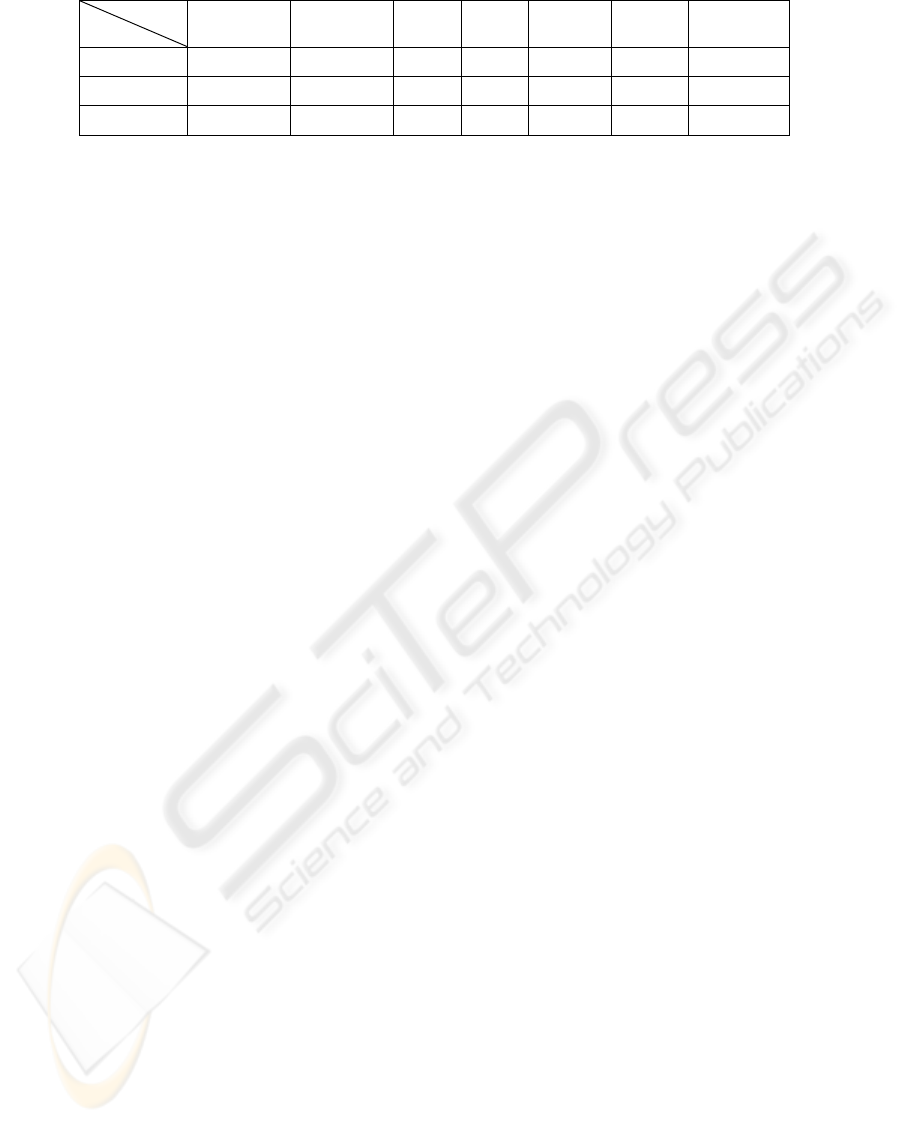
Table 4: Residual error of different pairs of medical images
Method
Group
RANSAC MLESAC MGA SEA SEA+T FMEA FMEA+T
MG1 6.537 1.664 1.584 1.702 1.887 1.637 1.621
MG2 8.025 2.124 1.621 2.116 2.075 1.936 1.907
MG3 29.06 3.032 2.135 2.626 2.651 2.452 2.276
5 CONCLUSION
In this paper, we described a novel competitive
evolutionary agent-based approach to trifocal tensor
estimation, which employs a new competitive
strategy to control the breeding number of new
agents and reduce the chance of reproducing unfit
ones. It focuses on the reproduction behavior to
reduce the computation time, and produces results
commensurate with, or superior to, that of SEA. The
experimental results indicate that the proposed
method attains a high level of performance in terms
of accuracy and computational efficiency. It can
obtain an optimal (or near optimal) result in the
solution space and is robust to outliers, even when a
large number of outliers are involved.
By accurately estimating the trifocal tensor, it
will now be possible to generate 3D views of the
sequence of 2D images. This brings the authors
closer to their ultimate goal, the real time generation
of 3D views during a laparoscopic procedure in
order to enhance features, in particular obscured
features, to the surgeon. This requires that the
geometric data are estimated as fast and accurately
as possible. The novel finite multiple evolutionary
agent-based approach presented here allows us to do
this.
REFERENCES
Faugeras O. and Papadopoulo T., 1998. “A nonlinear
method for estimating the projective geometry of 3
views”, in Proc. 6
th
International Conference on
Computer Vision, pp.477-484.
Hartley R. and Zisserman A., 2000. “Multiple view
geometry in computer vision,” Cambridge University
Press.
Hartley R. and Vidal R., 2004. “The multibody trifocal
tensor: motion segmentation from 3 perspective
views”, in Proc. Computer Vision and Pattern
Recognition, vol. 1, pp.769-775.
Hu M.X. and Yuan B.Z., 2002. “Robust Estimation of
Trifocal Tensor using Messy Genetic Algorithm”, in
Proc. 16
th
International Conference on Pattern
Recognition, vol. 4, pp.347-350.
Hu M.X. and Yuan B.Z., 2002. “Novel estimation of
trifocal tensor using GMM,” IEE Electronics Letters,
vol. 38, no. 19, pp.1094-1095
.
Hu M.X., Dodds G. and Yuan B.Z., 2004. “Evolutionary
agents for epipolar geometry estimation”, in Proc.
IEEE International Conference on Image Processing,
2004, vol. 2, 1843-1846.
Liu J.M, Tang Y.Y. and Cao Y.C., 1997. “An evolutionary
autonomous agents approach to image feature
extraction”, IEEE Trans. On Evolutionary
Computation, vol. 1, no. 2, pp. 141-158.
Matei B., Georgescu B., Meer P., 2001. “A versatile
method for trifocal tensor estimation,” in Proc. 8
th
International Conference on Computer Vision, vol. 2,
pp.578-585.
Quan L., 1994. “Invariants of 6 points from 3 uncalibrated
images”, in Proc. European Conference on Computer
Vision, vol. 2, pp.459-470.
Shashua A., 1995. “Algebraic functions for recognition,”
IEEE Transactions on Pattern Analysis and Machine
Intelligence, vol. 17, no. 8, pp. 779-789.
Torr P. H. S., 1995. “Outlier detection and motion
segmentation,” PhD thesis, University of Oxford
.
Torr P. H. S. and Zisserman A., 1997. “Robust
parameterization and computation of the trifocal
tensor,” Image and Vision Computing, vol. 15, pp.
591-605.
Veenman C.J., Reinders M.J.T. and Backer E., 2003. “a
cellular coevolutionary algorithm for image
segmentation”, IEEE Trans. Image Processing, vol.
12, no. 3, pp. 304-316.
MULTIPLE VIEW GEOMETRY ESTIMATION BASED ON FINITE-MULTIPLE EVOLUTIONARY AGENTS FOR
MEDICAL IMAGES
209
