GA BASED DATA FUSION APPROACH IN AN INTELLIGENT

INTEGRATED GPS/INS SYSTEM

Ali Asadian, Behzad Moshiri

Control and Intelligent Processing Center of Excellence

Department of Electrical and Computer Engineering, University of Tehran, Tehran, Iran

Ali Khaki Sedigh

Control and Intelligent Processing Center of Excellence

Department of Electrical Engineering, University of K.N.T, Tehran, Iran

Caro Lucas

School of Cognitive Sciences, Institute for Studies on Theoretical Physics and Mathematics

Tehran, Iran

Keywords: Genetic optimization, Adaptive Network based Fuzzy Inference System (ANFIS), Global Positioning

System (GPS), Inertial Navigation System (INS).

Abstract: A new concept regarding to the GPS/INS integration, based on artificial intelligence here is presented. Most

integrated inertial navigation systems (INS) and global positioning systems (GPS) have been implemented

using the Kalman filtering technique with its drawbacks related to the need for predefined INS error model

and observability of at least four satellites. Most recently, an INS/GPS integration method using a hybrid-

adaptive network based fuzzy inference system (ANFIS) has been proposed in literature. During the

availability of GPS signal, the ANFIS is trained to map the error between the GPS and the INS. Then it will

be used to predict the error of the INS position components during GPS signal blockage. As ANFIS will be

employed in real time applications, the change in the system parameters (e.g., the number of membership

functions, the step size, and step increase and decrease rates) to achieve the minimum training error during

each time period is automated. This paper introduces a genetic optimization algorithm that is used to update

the ANFIS parameters with the INS/GPS error function used as the objective function to be minimized. The

results demonstrate the advantages of the genetically optimized ANFIS for INS/GPS Integration in

comparison with conventional ANFIS specially in the cases when facing satellites’ outages. Coping with

this problem plays an important role in assessment of the fusion approach in land navigation.

1 INTRODUCTION

Ever since the artificial intelligence, has been

considered as a powerful and applicable tool in

engineering modeling, computation, nonlinear

function approximation, system identification and

estimation theory. The neuro-fuzzy models have the

connectionist structure of neural networks combined

with flexibility and intuitive learning capabilities of

fuzzy systems. A variety of Inference engines and

learning algorithms have been discussed in the

literature (Mackay, 2003). ANFIS is one of the most

popular algorithms that has been used for different

purposes such as system identification, signal

processing, pattern recognition, control of dynamical

systems and prediction (Shing et al., 1993). As

discussed it has a hybrid learning method based on

gradient descent and least square estimation.

Another new method which can be categorized in

the intelligent approaches is genetic algorithms. GAs

as function optimizers are global optimization

techniques based on natural selection (Goldberg,

1989 ; Michalewicz, 1996). This form of

evolutionary algorithm evolves throughout

generations improving the features of potential

216

Asadian A., Moshiri B., Khaki Sedigh A. and Lucas C. (2005).

GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 216-221

DOI: 10.5220/0001171802160221

 SciTePress

solutions by means of biologically inspired

operations. GAs are presented as a tool to optimize a

certain objective function. For instance in GAs have

been combined with extended kalman filter in order

to increase the overall performance (Stroud, 2001).

Several usages of GAs have been found in the

literature (Geisler et al., 2002 ; Loebis et al., 2003 ;

Simske, 2003). Here in this paper we will focus on

optimization of the ANFIS network with GAs in the

field of navigation applications. It will be shown that

the mentioned estimator filter has an excellent

performance when encountering satellites’ outage as

a great benchmark in assessment of fusion approach.

2 OVERVIEW

It’s well established that global positioning system

(GPS) can provide position and velocity information

of moving platforms with consistent accuracy

throughout the surveying mission. The limitations of

GPS are related to the loss of accuracy in the

narrow-street environment, intentional disruption of

the service, poor geometrical-dilution-of-precision

(GDOP) coefficient and the multipath reflections.

GPS-based navigation system requires at least four

satellites, so a major drawback of GPS dependence

navigation systems is that their accuracy degrades

significantly with satellites’ outages. Signal outage

is more significant for land vehicle positioning in

urban centers, which takes place when encountering

highway overpasses or tunnels. Besides the presence

of noise in GPS signals, necessitates the use of

narrow bandwidth filters which limits also the

dynamic of the vehicle. So it is suitable to integrate

this type of navigation system with a different type

of navigation system in order to reach a greater

autonomy.

From this point of view, the inertial navigation

system (INS) is ideal. In opposition with receiving

signals from satellites, in the case of GPS, the

autonomy of INS is provided by the functioning

principle, which is based on measurements of inertia

of the vehicle, linear accelerations, and angular

velocities. An INS measures the linear acceleration

and angular rates of moving vehicles through its

accelerometers and gyroscopes sensors. The main

interest is the position determination, which is

possible after a double integration of the

accelerations to obtain linear displacements and a

single integration of the angular velocities to obtain

the angles of rotation. The INS accuracy degrades

over time, due to the unbounded positioning errors

caused by the uncompensated gyro and

accelerometer errors affecting the INS

measurements. The degradation is much faster for

low-cost INS systems. INS provides high-accuracy

three-dimensional positioning when the GPS

positioning is poor or unavailable over short periods

of time (e.g., due to poor satellite geometry, high

electromagnetic interference, high multipath

environments, or obstructed satellite signals). In

addition, the INS system provides much higher

update positioning rates compared with the output

rate conventionally available from GPS (Farrel,

1999). Anyway in order to utilize the benefits of

these two navigation sensors and gain the

advantages of the data fusion, we fuse the data

gathered by each and use integrated system.

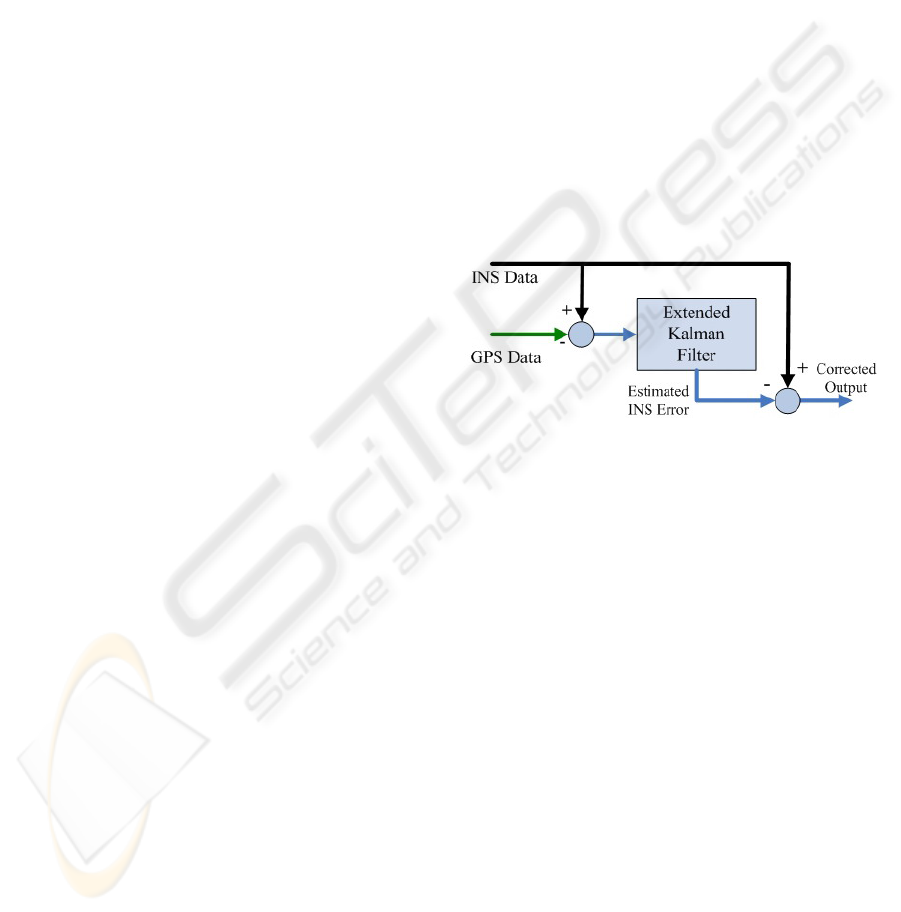
Traditional integration which is accomplished by

means of Kalman filtering has been shown in Figure

1. Where the INS outputs are compared to the

outputs of the GPS. The errors in between are

subjected to Kalman filtering, which enhances the

performance of the navigation system by removing

the effect of residual random errors during the

surveying process (Mayhew, 1999).

As mentioned in the literature, Kalman filter

provides poor prediction of position errors, when

encountering satellites’ outages. In order to prevent

or, at least, to reduce the impact of accuracy

decreasing when GPS becomes unavailable, an

adaptive network based fuzzy inference system

(ANFIS) has been used on a simplified 2-

Dimensional navigation model, built and trained

using data from stand-alone INS, on one hand, and

from the GPS on the other hand (Hiliuata et al.,

2004). For this purpose, the GPS-derived positions

and velocities are excellent external measurements

for updating the INS, thus improving its long-term

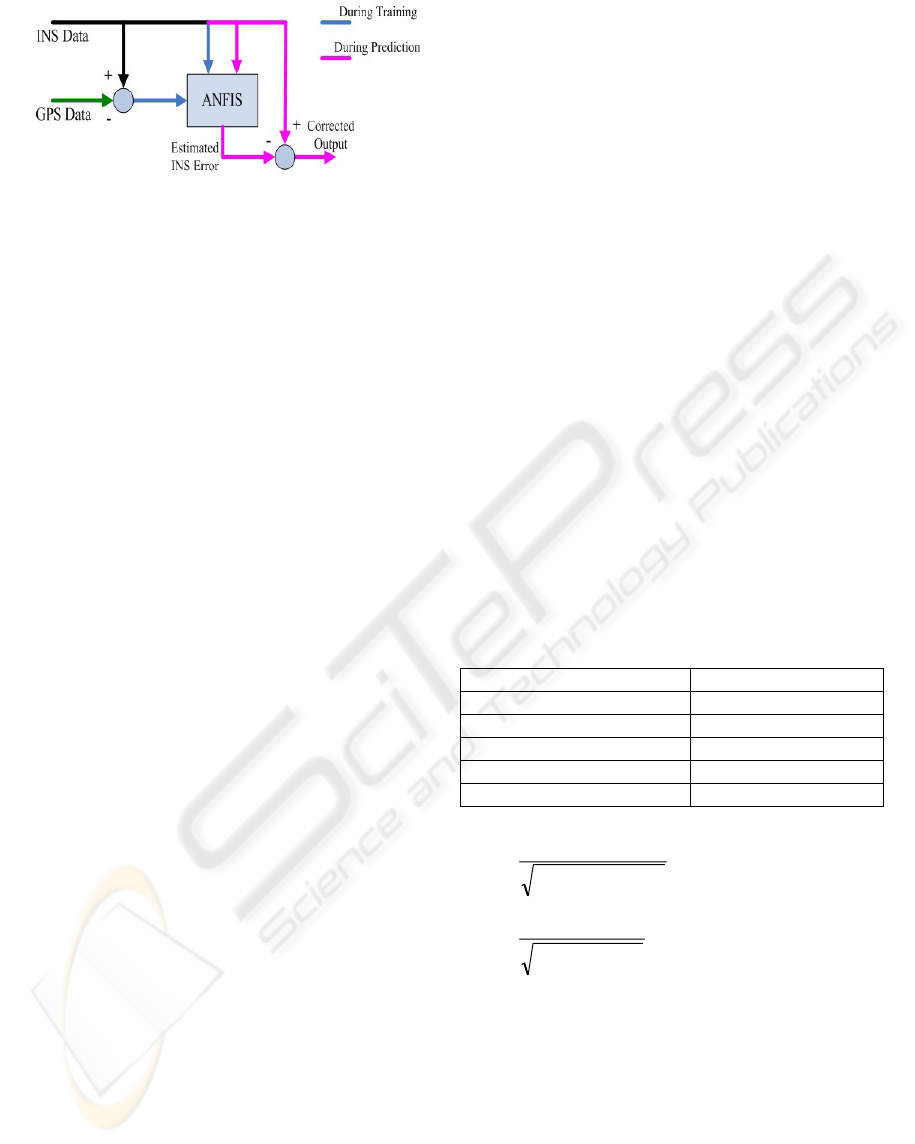
accuracy. This fact has been illustrated in Figure 2.

The ANFIS could be built and trained during the

availability time of reference system. Passing the

INS data through ANFIS will procure a better

accuracy when the reference source is missing. In

the absence of the GPS information, the system will

perform its task only with the data from INS and

with the intelligent correction algorithm. A complete

investigation has been performed to solve the

navigation problem with real data via ANFIS

network (Wang et al., 2003).

Figure 1: Traditional GPS/INS integration using

Kalman filtering

GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM

217

3 GENETIC ALGORITHM

OPTIMIZATION

The GAs behave much like biological genetics and

are an attractive class of computational models that

mimic natural evaluation to solve problems in a

wide variety of domains (Luke et al., 1998). They

introduce a population of individual solutions to an

optimization problem and then evaluate the fitness

of each individual in this population. Limited by the

laws of natural selection, individuals with most

suited elements in a population and better

performance survive while those with weak

performance are weeded out. The optimization

process gets its dynamic by developing new

generations of potential solutions and evaluating the

degree of fitness of each generation and allowing it

to proceed if it satisfies specific selection criterion

which is usually based on a fitness-proportional

selection.

GAs map a problem onto a set of strings (the

chromosomes), each string representing a potential

solution. The three most important aspects of using

GAs are :

• definition of the objective function

• definition and implementation of the

genetic representation

• definition and implementation of the

genetic operators

The speed of genetic algorithm depends heavily

on the encoding scheme of the chromosomes and on

the genetic operators that work on these

chromosomes (Geisler et al., 2002).

The following is a pseudo code for a general

GA :

• Generate the initial parent population

• Evaluate the initial parent population

• Loop until termination criteria is satisfied

• Select chromosomes for reproduction

• Create offspring using reproduction

operators such as crossover and

mutation

• Replace parent population by offspring

population

• Return fittest chromosome of last parent

population

4 MATHEMATICAL MODEL OF

INTEGRATED GPS/INS

SYSTEM

Several mathematical models have been proposed in

order to integrate INS and GPS sensors (He, et al. ,

1998). The number of states generally determines

the accuracy of the modeling. Different models have

been utilized in the literature. Here we use the model

explained below (Azimi-Sadjadi, 2001).

Measurements of accelerometers and gyros are

expressed in the platform frame while the GPS

measurements are given in an rectangular Earth

Centered Earth Fixed (ECEF) frame. The geodetic

coordinate system is defined according to the

familiar longitude (

), latitude(

), and height( h )

coordinate system. For this system of coordinates,

the Earth’s geoid is approximated by an ellipsoid.

The defining parameters for the geoid according to

the WGS84 reference frame are given in Table 1.

and equations (1-2). The relation between these two

coordinate system is also given by (3).

Value Parameter

6378.137 km a (semi major axis)

6345.752 km

b (semi minor axis)

7.292115×10

−5

Rad/Sec

(earth's angular velocity)

3.352511×10

−3

f (ellipsoid's flatness)

0.05781 e (ellipsoid's eccentricity)

322

)}(sin1{

)1(

−

(1)

)(sin1

−

(2)

⎟

⎠

⎞

⎜

⎝

⎛

+−

⎟

⎠

⎞

⎜

⎝

⎛

)sin())1((

)sin()cos()(

)cos()cos()(

φλ

heR

(3)

For simplicity we assume that the gyros and the

accelerometers are aligned with the axis in the

platform frame. Also, we assume that the body

frame and the platform frame are aligned, and the

center of the coordinate system is the same for both

frames. The transformation from body frame to local

Figure 2: Intelligent GPS/INS integration with ANFIS

Table 1: Parameters of WGS84 reference frame

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

218

geographical frame is calculated at every moment as

follows :

dtRdR

gbgbgb

Ω=

(4)

⎟

⎠

⎞

⎜

⎝

⎛

−

=Ω

q 0

(5)

⎟

⎠

⎞

⎜

⎝

⎛

+−

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

φω

)tan(

)sin(

)cos(

(6)

is the inertial angular rate expressed in the

body frame which can be expressed as follows in

(6), where

rqp )

(

is the measured angular rate, and

rpq

bbb ) (

is the bias in the angular rate

measurement.

The GPS signal consists of a clock signal and a

navigation message that are amplitude modulated.

The GPS receiver receives the signal corrupted by

noise and other sources of error. By neglecting the

ionospheric and tropospheric errors which are highly

correlated, the observation equations or

pseudoranges provided by

i GPS satellite, have

the following form :

δρ

cZZYYXX

msimsimsii

+−+−+−=

222

)()()(

(7)

where

),,(

mmm

ZYX and ),,(

sisisi

ZYX are the

coordinates of the receiver and the

i satellite

respectively.

c is speed of the light and

equals

clock drift.

Note that the above hypothesis is valid in most

land navigation purposes. In order to simplify the

design process in future, it’s assumed that the

receiver coordinates in ECEF frame can be extracted

from the pseudoranges through out the use of an

external extended kalman prefilter. We suppose this

fact for the rest of this research so the outputs of the

GPS sensor are supposed to be the receiver’s

coordinates. The GPS clock drift and the INS

equations constitute key dynamics in an integrated

INS/GPS system and could be expressed as (8-13)

equations. where g is the gravitational acceleration,

wvu

aaa )

(

is the accelerometer measurement

expressed in the body frame,

wvu

bbb ) (

is the

accelerometer measurement bias again expressed in

the body frame.

w ,

w and

w are vectors of

brownian motion process with zero means and

known covariance matrixes.

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

1 0 0

)cos()(

0 0

{}

Eie

DNie

Eie

dwdt

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

+++

+−

−

⎟

⎠

⎞

⎜

⎝

⎛

)cos(2

)cos(2)sin(

)tan(

)sin(2

)tan(

λφ

φλ

φω

φφω

φω

dwdt

d +

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

dwdt

d +

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

ttt

dwdtaxdx +−=

dtxd

(8-13)

5 ARCHITECTURE OF THE

PROPOSED NETWORK

In the previous studies the ANFIS parameters (

step size,

as step increase rate and

as step

decrease rate) were tuned manually by trial and error

to prove the efficiency of ANFIS network for

INS/GPS integration (Wang et al., 2003). Changing

these parameters could significantly affect ANFIS

prediction capabilities and have considerable effect

in our application while changing the number of

fuzzy rules is unlikely to produce any significant

impact. Therefore, these parameters’ tuning process

should be automatized to allow system utilization in

real-time applications so it’s suggested here that

ANFIS network parameters shall be tuned

automatically by means of genetic algorithms. It’s

proposed that a GA to be used to optimize ANFIS

network parameters during the training mode with

the objective of achieving the minimum training

error. This new scheme has been illustrated in Figure

3. The proposed automatization process will cause

considerable reduction of position error than those

reported before.

GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM

219

17 separate ANFIS networks were developed for

integrating the INS/GPS for the whole state vector

components. All the networks have similar

architecture but different parameters. During the

training process, the mentioned parameters can be

tuned for each network separately to achieve the

minimum training error for each time period and for

each state vector component. In the training mode

the network’s inputs include INS outputs and time

(T) while its desired output is

INS

E as described in

equation (14) where

denotes the corresponding

position. The system concept is to train the network

during the GPS availability periods and then to

predict the INS error signal once the GPS outage

occurs.

INSGPSINS

PPE −= (14)

….After training process, the ANFIS network will

produce an INS error, which can be denoted as

ANFIS

E . Then the modeling error is defined as (15) :

ANFISINS

EEE −= (15)

….Then by defining the root mean square of the

model error for n observations as (16) :

ERMSE = (16)

….The objective function for the GA is chosen to

minimize the RMSE by optimizing ANFIS network

parameters.

6 SIMULATION RESULTS

The simulation was made with a relatively low IMU

sample rate, 10 Hz. The GPS pseudoranges are

available with the rate of 1 Hz. The kinematic data

used in this study was generated by Satnav toolbox

created by GPSoft. In our test, the following flight

profile was used. This flight path (Figure 4)

contains one pitch manoeuver in the beginning and

one 90 degree turn in the middle of scenario

The numerical parameters were selected as

below. The last parameters model a typical quartz

TCXO with frequency drift rate of

secsec/10

9−

-4

10905.4

×=

∑

0.09

∑

-5

10=

∑

0015.0

−

002.0

The GA was implemented using a genetic

algorithm optimization toolbox developed in

MATLAB 7 package. The algorithm utilized a

crossover rate of

=0.75 and a probability of

mutation of

=0.001. The proposed network was

trained using the GA architecture described before.

18 generations were created by the GA algorithm to

search for the minimum RMSE. The search

converged successfully to the minimum RMSE after

18 generations. The ability of the two networks in

correct prediction is compared in Figures 5 and 6.

It’s clear that the second network’s output is a little

bit better than the first one’s.

The optimal parameters that led to the minimum

of RMSE are :

=0.0298,

=1.6935 and

=0.6221. After completion the training process,

then a complete GPS signal outage of 120 seconds

starting at time 450 was intentionally introduced

within the GPS data and both algorithms were used

to predict the INS dynamic during the outage period.

In order to save computational effort, in this case

GA optimization is only applied during satellites’

Figure 3: Intelligent GPS/INS integration with optimized

ANFIS with GA

ure 4: The fli

ht scenario

Figure 5 : Position tracking of the ANFIS

Figure 6: Position tracking of the optimized ANFIS

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

220

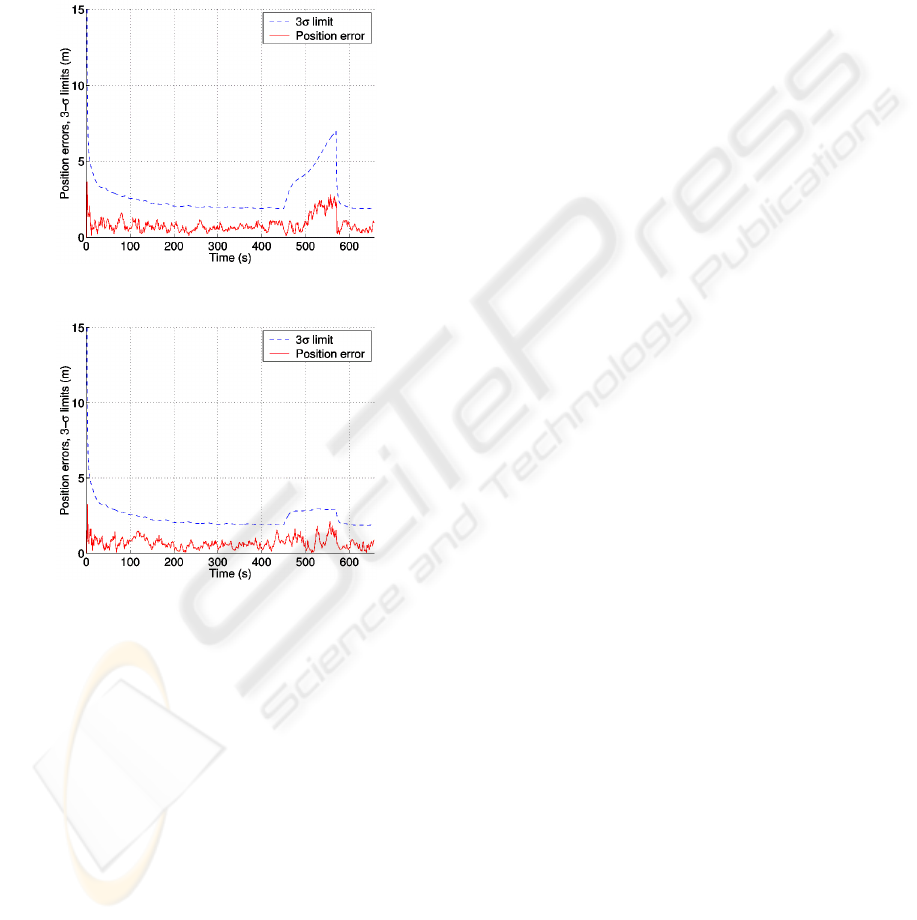
outage. The RMSE of the two networks during this

period were obtained as 2.684 for ANFIS and 1.123

for optimized ANFIS versus meters.

It is obvious that the second network has a better

performance than the alone ANFIS network as a

result of genetic optimization. In the second case an

improvement index of 58.2% in position estimation

could be achieved. This fact could also be seen in

the following figures :

7 CONCLUSION

Genetic optimization applied to the adaptive neuro-

fuzzy navigation system. It has been used as a

method to improve the estimation problem .

Obtained results demonstrated the improved

performance of this method over conventional

ANFIS network. Althought the proposed solution

needs more computation effort but it showed

outstanding performance in critical situations such

as satellites’ outages which is much likely in land

navigation. To emphasize on the above advantage,

the number of visible satellites intentionally

degraded to zero during the simulation. The figures

clearly prove the estimation improvement.

REFERENCES

Mackay, D. J. C., 2003. Information theory, inference and

learning algorithms. U.K., Cambridge University

Press.

Farrel, J. A. and Barth, M., 1999. The global positioning

system and inertial navigation. U.S.A, New York:

McGraw-Hill.

Shing, J. and Shang, R., 1993. ANFIS : Adaptive-

Network-based Fuzzy Inference System. IEEE

Transactions on Systems Man and Cybernetics, vol.

23, no. 3, pp. 665-685.

Stroud, P. D., 2001. Kalman-Extended genetic algorithm

for search in nonstationary environments with noisy

fitness evaluations. IEEE Transactions on

Evolutionary Computation, vol. 5, no. 1, pp. 66-77.

Geisler, T., and Manikas, T. W., 2002. Autonomous robot

navigation system using a novel value encoded genetic

algorithm. In Proc. 45th IEEE International Midwest

Symposium on Circuits and Systems, p. 45-48.

Loebis, D., Sutton, R. and Chudley, J., 2003. A fuzzy

kalman filter optimized using a genetic algorithm for

accurate navigation of an autonomous underwater

vehicle. In Proc. MCMC2003 Conference, Girona,

Spain, pp. 19-24.

Simske, S. J., 2003. Navigation using hybrid genetic

programming : initial conditions and state transitions.

HP intelligent enterprise Tech. Lab., Tech. Report,

Palo Alto.

Luke, S. and Spector, L., 1998. A revised comparison of

crossover and mutation in genetic programming. In

Proc. 3th Annual Genetic Programming Conference

(GP98). San Fransisco: Morgan Kaufmann, pp. 208-

213.

Hiliuta, A., Landry, R., Jr. and Gagnon, F., 2004. Fuzzy

correction in a GPS/INS hybrid navigation system.

IEEE Transactions on Aerospace and Electronic

Systems, vol. 40, no. 2, pp. 591-600.

Wang, J. H. and Gao, Y., 2003. Evaluating the accuracy of

GPS positions under severe signal-degradation using

adaptive-network-based fuzzy inference systems

(ANFIS). In the 50th CASI Annual General meeting

and Conference, Canadian Aeronautics and Space

Institute, Montréal, Quebec, Canada.

Mayhew, D. Mc. N. , 1999. Multi-rate sensor fusion for

GPS navigation using kalman filtering. M.S.

thesis,

Dept. Elect. Eng., Virginia Polytech. Institue and State

University, Virginia, USA.

He, X., Chen, Y. and Iz, H. B. , 1998. A reduced-order

model for integrated GPS/INS. IEEE AES Systems

Magazine, pp. 40-45.

Azimi-Sadjadi, B., 2001. Approximate nonlinear filtering

with applications to navigation. Ph.D. dissertation,

Dept. Elect. Eng., Maryland University, College Park.

ure 7: Position error of ANFIS networ

ure 8: Position error of o

timized ANFIS networ

GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM

221