USE OF THE COG REPRESENTATION TO CONTROL A ROBOT

WITH ACCELERATION FEEDBACK

Frédéric Colas, Eric Dumetz, Pierre-Jean Barre

Technological Research Team – ERT CEMODYNE, ENSAM, 8 avenue Louis XIV, 59046 Lille Cedex, France

Jean-Yves Dieulot

Ecole Polytechnique Universitaire de Lille, LAGIS, UMR 8146 CNRS, Cité Scientifique,

59651 Villeneuve d’Ascq Cedex, France

Keywords: Causal Ordering Graph, Industrial robot, Acceleration feedback, Jerk, Vibration control.

Abstract: A controller using acceleration feedback has been applied to a flexible robot for which the position and

velocity of the load are not measured. It is shown by using the Causal Ordering Graph (COG), that the

motor can be controlled by using acceleration feedback and that it allows an exact tracking of the motor

position, irrespective of the non-linear flexibilities of the axis and of the measurement disturbances. This

easy-to-tune algorithm, in which main control parameters are the modal masses of the motor and load part

and only consists of a positive acceleration feedback plus a PD controller, has been validated on an

industrial 3-axis robot.

1 INTRODUCTION

The demands for smaller operation times, low-

energy consumption and lower robot costs are the

main motivations for the use of lightweight high-

speed robots. However, high speed and accelerations

supported by such flexible robots lead to undesirable

vibrations. Since vibrations deteriorate the

equipment and affect the precision of the positioning

device, their damping should be considered as a

prerequisite to any further increase of performances.

As will be explained below, the combination of this

underdamped behaviour and the lack of measures on

the end-point makes it impossible for the current

industrial control structures to perform rapid and

robust closed-loop dynamics.

Obtaining accurate control-oriented models of

complicated flexible structures is not an easy task.

Whereas finite element method (FEM) allows the

different modes of deformation of a structure to be

understood, they are not suitable for control

purposes. A simpler model can be obtained when

decomposing the structure in a set of rigid bodies

linked by spring elements using Assumed Modes

Methods (AMM). Meirovich have proven to be able

to represent the dynamic structure of a CNC axis

drive (Meirovich, 1994). In such a complex structure

as a flexible Cartesian robot, it has been found

experimentally that the springs’ stiffness exhibit

large variations whereas modal masses remain

nearly constant. Moreover, it is impossible to

measure the load position and velocity in the

industrial context, since the cost of measurement

devices (e.g. a laser or a camera) is prohibitive. As a

consequence, only the motor part is controlled in

closed loop whereas the load is controlled in open-

loop, and this fundamental aspect is not often

accounted for in the literature (Béarée, 2004). It has

been shown (Béarée, 2004) that the combination of

low damping and the lack of measures on the load

results in poor control performances. As an

alternative to load position measurements, the use of

an accelerometer mounted on the effector’s end can

provide additional information at a reasonable price.

Since it is impossible in practice to derive the

velocity and position of the load from an integration

of the acceleration signal owing to the important

measurement noise, the acceleration feedback

should be directly embedded in the controller.

Acceleration feedback has been be expressed in

the framework of optimal control (Luo and Saridis,

1985) for which a compensation of non-linear terms

enforces the tracking error to converge

asymptotically to zero. This method, however, needs

to measure the torques at the motor shafts and the

Colas F., Dumetz E., Barre P. and Dieulot J. (2005).

USE OF THE COG REPRESENTATION TO CONTROL A ROBOT WITH ACCELERATION FEEDBACK.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 25-31

DOI: 10.5220/0001171900250031

 SciTePress

joint accelerations, and is not easily applicable in an

industrial context, where such complete and accurate

measurement is not available. Indeed, the tuning and

the practical implementation of this algorithm (Mc

Inroy and Saridis, 1990) meets many difficulties

such as the obtaining of angular accelerations and

torque measurements which require further

computations or approximations. It has been shown

experimentally that an increase of the sampling

frequency or the feedback gains leads to instability.

In summary, there have been few experimental

results actually based on the measured acceleration

information.

In this paper, the same acceleration feedback

algorithm of (Luo and Saridis, 1985) is deduced by

using the Causal Ordering Graph (COG introduced

by Hautier, 2004) on a robot modelled by a two

mass model with a spring with lumped stiffness

parameters. The COGs consist in a graphical

language for describing the dynamics of physical

systems and provide general methodology to

determine their control structures.

Contrary to Luo and Saridis algorithm, the

developed controller just needs the value of the

modal masses and is thus easier to tune. Two figure

cases will be tackled, corresponding to the industrial

context: the tracking of a reference trajectory of the

motor, and the tracking of a reference trajectory of

the load for which the motor reference motion is

computed off-line.

The paper is organized as follows: the modelling

approach of the robot is described in the first part.

The acceleration feedback algorithms are developed

next section. Finally, real-time validations are

presented for an industrial pick-and-place robot.

2 A LUMPED MASS-SPRING

MODEL OF AN INDUSTRIAL

ROBOT

The robot which is considered in this study is an

industrial Cartesian robot, which exhibits an average

cycle time of 3 s, a mass of 750kg and accelerations

up to 4m.s

-2

. The robot cycle time is a key parameter

in the overall process optimisation. The vibrations

due to the robot flexibilities (in particular that of the

vertical axis) are quite underdamped, and become

critical when exceeding more than 2mm (or 0.3mm

on the motor reference trajectory), which restrains

the performances and limits the cycle time.

In this part, it will be recalled how classical

modelling methods allow to design a control-

oriented model which respects the physics of the

structure of such a flexible robot and allows the

damping of vibrations. A presentation of such

methods can be found in more details in (Meirovich,

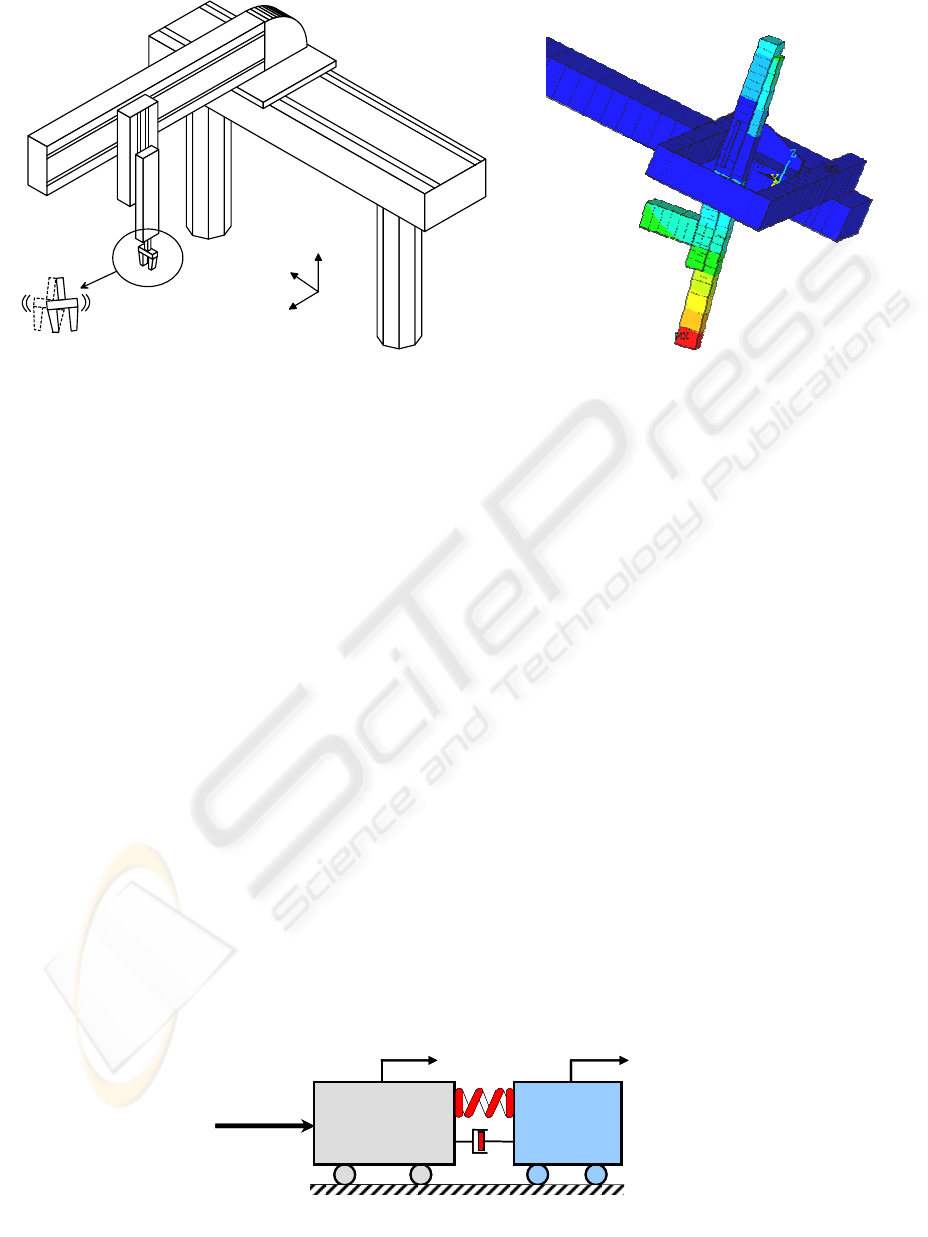
Figure 1: Identification of the main deformation mode (Horizontal motion X axis: Bending of Z) with ANSYS

Figure 2: Two-mass-spring model of a Cartesian robot (X axis)

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

1994), (Ellis, 2000).

The Finite Elements Method is a classical tool

which enables an accurate modelling of the

dynamical behaviour of a flexible system, using a

polynomial approximation of the deformations of

elements such as beams, plates, etc... Figure 1

shows the first deformation mode due to the bending

of the vertical Z-axis during the horizontal motion of

the robot. The evolution of the other deformation

modes during the motion of the robot in its working

space is not intuitive.

Whereas this method allows the behaviour of the

robot to be understood, its complexity prevents its

use for control purposes. An alternative method to

the modelling of small deformation consists of

decomposing the structure in a set of rigid bodies

which are linked by spring elements using the

method of Assumed Modes. A model with lumped

parameters for which the stiffness of the spring

depends on the position of the load mass in the

working space allows the first deformation modes to

be represented (Meirovich, 1994). This study will be

limited to the modelling and control of the first

deformation mode, i.e. projection of the bending of

the vertical axis on the horizontal plane during the

motion of the X axis. The dynamical model of the

motion can be represented by a two-mass model

with a spring of variable stiffness.

Modal analysis can be carried experimentally

using an impulse response obtained when exciting

the effector’s end with an impact hammer (Barre,

96). The signal is recorded using a spectrum

analyser. The variation of the modal parameters for

an horizontal displacement (axis X) is moderate but

becomes very important because of torsional

coupling when both the axis X and Y are moving.

All these parameters are lumped through the value

of the Z position. According to Figure 2, the

equations of model are:

(

)

(

)

11 2 1 2 1

mx k x x a x x u=−+−+

&& & &

(1)

()

(

)

22 1 2 1 2

mx k x x a x x=−+−

&& & &

(2)

()

kk gy=+ (3)

where u is the driving effort, x

and x

are

respectively the positions of the motor and the load

for the horizontal X axis, y

is the position of the

load for the transverse Y axis, m

and m

are

respectively the modal masses of the motor and the

load part, k is the modal stiffness. Experimental

results show that g(y

)=a.y

+b.

Consider an horizontal displacement, for which

-y

=α(x

-x

). The stiffness k is now a linear

function of the load position x

, with k=k

+aα(x

)+b+ay

The frequency of the main deformation mode

and the corresponding damping ratio are given:

111

(4)

3 ACCELERATION FEEDBACK

As discussed previously, the motor part can be

controlled in closed-loop whereas the load is

controlled in open-loop. Two control methods can

be employed, depending on the specifications that

are required by the user. As an example, one may

want to improve the cycle time while others want to

reduce the load’s vibrations to an acceptable level.

3.1 Tracking of the Motor Reference

Position

Since the concept of causality is important in the

comprehension of the physical phenomena, we used

a tool called the Causal Ordering Graph and

introduced by Hautier (Hautier, 2004). It allows us

to represent a system with elementary objects

defined using energetic considerations. When an

object does not store any information, the causality

will be defined as external and the output will be

derived directly as a function of the input. The

relation (R) is then called rigid:

If an object stores information, the causality is

internal and the output is a function of the energetic

state of the system. In this case, the relation (R) is

called causal, both the time and initial state are the

implicit inputs:

When the model of the process is established, the

control structure is deduced by inversion of the

COG. This model being made up of causal and rigid

relations, two different solutions for the inversion

result:

In a Rigid Relation, a bijective relation C

determines a control law using direct causal

inversion.

USE OF THE COG REPRESENTATION TO CONTROL A ROBOT WITH ACCELERATION FEEDBACK

In a Causal Relation, time acts implicitly so that

the accumulation effect induces an initial value and

the relation is not bijective any more. Thus, the

tuning value u

reg

is elaborated while taking into

account, at any moment, the value of y according to

its reference y

ref

. This inversion principle is nothing

but the measurement feedback principle.

Applying these rules, we obtain the COG

representation of the Motor Control which is shown

in Figure 3. The different relations are summarized

in Table 1. The overall control u is obtained by using

the model inversion principle and choosing C

and

as simple gain k

and k

(

)

(

)

22 11 1 1 1 2 1 1

MES REF REF MES REF MES

umx mx kx x kx x=++−+−

&& && & &

(5)

It allows a perfect tracking of the motor

irrespective of the non-linear flexibilities of the axis

and of the measurement disturbances. One can

recognize the simplified version of the acceleration

feedback algorithm of (Luo and Saridis, 1985). This

is the main advantage to use the COG formalism.

Indeed, the motor control algorithm is derived easily

by using this tool.

Table 1: Relations of the COG representation of the Motor

Control

Two-Mass-Spring Model Motor Control

111

()

load

RmxutF→=−

11 2 1 3 1

()

REF

ci reg

load

Rut

mx F C x C x

→=

++∆+∆

&& &

()

211

Rxx

→=

&&&

()

211

EF REF

Rxx

→=

&&&

()

311

→=

()

311

EF REF

→=

412

xx x→∆ = −

&& &

()

22 211

REG REF MES

ci ci

Ru Cxx→= −

()

5 spring

Fkx

→=∆

()

33 311

REG REF MES

ci ci

Ru Cxx→= −

6 viscous

Fax→=∆

922

MES

c load

Fmx→=

7 load spring viscous

RF F F→= +

load

→=

()

922

Rxx

→=

&&&

ure 3: COG re

resentation of the Motor Control

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

3.2 Load’s Vibrations control

The former method of control consists of enforcing

the motor to follow a prescribed trajectory.

Conventional controllers for Cartesian robot use a

reference trajectory for the motor position, which

does not guarantee performances for the dynamics of

the load. An alternative method consists of defining

a reference trajectory for the load (e.g. a trajectory

with no vibrations). The corresponding motor

reference trajectory is determined using model

inversion by differentiating relation (2):

()

(

)

() ()

1021 221

222

022 222

REF REF REF REF REF

REF REF

EF REF REF REF REF

ax k g x x g x x x

ax m x

kgx x gx x x

⎡⎤

′

=− + −

⎡⎤

⎣⎦

⎡⎤⎡ ⎤

′

++ +

⎣⎦⎣ ⎦

&& & &

&& &&&

(6)

Where x

REF

is the desired load trajectory

Equation (6) underlines that the third derivative

of the load position (the jerk) should be continuous

in order to avoid peaks on the motor acceleration

(and thus on the control). Indeed, the jerk value is

known to be a key tuning parameter (Barre, 2004).

4 EXPERIMENTAL VALIDATION

The main objective of the validation part is to show

that the acceleration feedback allows the cycle time

to be increased and the vibrations on the motor and

the load to be reduced. The experimental section is

organized as follows: the robot is moving diagonally

and results are compared for the tracking of a

prescribed motor trajectory, and for a load reference

trajectory with small and high jerk.

4.1 Material

The experimental validations are carried out on a

Cartesian 3-axis robot (figure 4). It was equipped

with a real-time “dSPACE 1103” control card. The

available measurements on the motor part come

from the actuator encoders of axis and an

Figure 4: Overview of the test-setup prototype (stroke [mm]: X-1000 Y-400 Z-800, maximum speed: 120m/min,

maximum acceleration: 4m.s

-2

Figure 5: Diagonal displacement, motor position - a)

-3

500 ms ,

-3

50 ms ,

Strong Full Line: Reference

Trajectory, Full line: Acc. Feedback, Dotted: Industrial loop.

USE OF THE COG REPRESENTATION TO CONTROL A ROBOT WITH ACCELERATION FEEDBACK

accelerometer located on the effector’s end gives the

load acceleration. A laser sensor (measuring

distance: 50mm / measuring range: 20mm) directly

gives the load position and is only used for

experimental verification.

The validations are undertaken for a

displacement y

-y

=α(x

-x

), where x

varies from

=0 to x

=900mm as before, and y

varies from

=0 to y

=400mm, with a height z=315mm. The

transverse Y-axis is controlled with a classical PI

controller, it has been checked that the actual

trajectory is nearly a straight line.

4.2 Tracking of a Motor Position

Reference Trajectory

The reference trajectory profile is a classical jerk-

limited bang-bang, i.e. the acceleration exhibits a

trapezoidal profile. The average modal masses taken

in the model and used for control (5) and simulations

are m

=350kg and m

=46kg (mean value), according

to that determined experimentally. The stiffness in

equations (1-3), according to the X-axis, is:

()

022 2

kk a x x bay

=+ − ++ (7)

where k

=1.27 10

N.m, α=0.444, a=-1.56 10

N. The

error on the stiffness correlation ranges from ±15%,

the mean uncertainties on modal masses are about

±25%. k varies from 1.27 10

N.m to 0.66 10

N.m,

i.e. about 100% during the whole course. In the case

considered, there exists an optimal value of the jerk

which limits the amplitude of vibrations (Béarée,

2004) (Barre, 2004), which is of 50ms

-3

One can see that the combination of the

acceleration feedback and an appropriate jerk allows

the rise time to be greatly improved while vibrations

almost vanish (Figure 5). In any case, the

acceleration feedback outperforms the conventional

loop (tuned at its best). The rise time is about 1.05s

when the robot is controlled with acceleration

feedback with a high jerk value, (1.15s with a jerk of

50ms

-3

) versus respectively 1.25s and 1.39s for the

conventional feedback with high and low jerk

values. The tracking performances of the

acceleration feedback algorithm allow to

compensate for the lag resulting from the use of a

low jerk value.

In theory, residual oscillations on the motor

position should not occur. Unperfect trajectory

following and oscillations can be due to non-linear

effects in axis coupling that where not taken into

account in the model, Coulomb friction effects and

effective variations of the modal masses. The results

on the load position show that high-amplitude

oscillations still occur whereas the cycle time is

improved.

4.3 Tracking of a Load Position

Reference Trajectory

An appropriate acceleration profile of the load is

now considered, for which the jerk is limited either

to 50ms

-3

or to 500ms

-3

. The trajectory will be

chosen to be the same as the reference trajectory of

the motor which was chosen in the previous

validation scheme. The motor reference trajectory is

thus derived using equation (6).

One can find that the damping is quite better

with acceleration feedback (one significant peak),

while the cycle time (obtaining of a near-steady state

value) reduces to 1s versus 1.15s for the

conventional algorithm. The results with an

appropriate jerk show that the load can be damped

very quickly (the oscillations are not even visible by

the operator, and with an amplitude under 0.2mm)

with far better performances than the conventional

algorithms (with or without jerk). Simulation results

are good enough, considering that the true variation

of modal masses was not taken into account.

Figure 6: Diagonal displacement, load position - a)

-3

500 ms ,

-3

50 ms ,

Strong Full Line: Reference

Trajectory, Full line: Acc. Feedback, Dotted: Industrial loop

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

Figure 6 shows the robustness of the acceleration

feedback with respect to modelling errors and

nonlinearities (considering that modelling errors are

quite important, more than 20% for each parameter).

The conventional controller is unable to compensate

the variations of stiffness as shown in figure 7

(oscillations are up to 3mm which is far too much for

the application considered). Oscillations are quite

underdamped with a low jerk. Nevertheless, the

gain on the cycle time is quite important (more than

0.15s), the amplitude of the oscillations do not

exceed ±0.5mm, which is quite satisfactory for our

application.

5 CONCLUSION

An acceleration feedback algorithm has been

determined by using the COG methodology. It

allows, in theory, an exact tracking of the motor

position. Moreover, model inversion allows an

appropriate motor reference to be derived to control

the load. This algorithm has been successfully

applied to an Industrial Robot which dynamics is

modelled by a two-mass spring with lumped

parameters and in the case of the load’s vibration

control, the Acceleration Feedback Controller nearly

eliminates the vibrations on the load. This may allow

to increase the performances of such manipulators

and to improve greatly the cycle time.

REFERENCES

Hautier, J.P., Barre, P.J., 2004. The Causal Ordering

Graph, a tool for system modelling and control law

synthesis. Studies in informatics and Control Journal,

Vol. 13 n°4,p265-283.

Barre, P.J., Hautier, J.P., Charley, J., June 24-27, 1996.

The use of modal analysis to improve the axis control.

Fourth International Congress on Sound and

Vibration, St Petersburg, Russia, pp. 1531-1538.

Barre, P.-J., Bearee, R., Borne, P., Dumetz, E., In press,

2004. Influence of a Jerk Controlled Movement Law

on the Vibratory Behaviour of High-Dynamics

Systems. Journal of Intelligent and Robotic Systems.

Béarée, R., Barre, P.J., Bloch, S., 2004. Influence of high

feed rate machine tool control parameters on the

contouring accuracy. Journal of Intelligent and

Robotic Systems, 40, p 321-342.

Luo, G., Saridis, G., 1985. L-Q design of PID controllers

for robot arms. IEEE Journal of Robotics and

Automation, 1, p152 – 159.

Meirovich, L., 1994. Principles and Techniques of

Vibrations, Prentice Hall.

Ellis, G., 2000. Control system design guide, Academic

press, Boston, 2

edition.

McInroy, J.E., Saridis, G., 1990. Acceleration and torque

feedback for robotic control: experimental results. J

Robotic Systems, 7, p 813-832.

USE OF THE COG REPRESENTATION TO CONTROL A ROBOT WITH ACCELERATION FEEDBACK