DEVELOPMENT OF POWER ASSIST ON OMNI-DIRECTIONAL
MOBILE WHEELCHAIR CONSIDERING
OPERATIONALITY AND COMFORT
Juan Urbano, Kazuhiko Terashima, Takahiro Nishigaki, Takanori Miyoshi
Department of Production Systems Engineering, Toyohashi University of Technology
Hibarigaoka 1-1, Toyohashi, 441-8580, Japan
Hideo Kitagawa
Department of Electronic Control Engineering, Gifu National College of Technology
Kamimakuwa, Motosu, Gifu, 501-0495, Japan
Keywords:
Omni-directional wheelchair, power assistant, fuzzy reasoning, tuning system, driving comfort.
Abstract:
In this paper, a power assist system of Omni-directional Mobile Wheelchair(OMW) for attendants aiming at
the reduction of incidence by operation of attendants is presented. The OMW presented in this paper, has
3 degrees of freedom, so it is important to consider operationality. The control system must be developed
considering both operationality and comfort. A Power assist controller using fuzzy reasoning is proposed to
estimate the navigation direction for the force given by the attendant, and the necessity of parameter tuning in
the membership functions is described according to the individual characteristics. Further, the second order
lag controller which transforms the force given by the attendant into the velocity of OMW, is presented to
develop the rider’s comfort.
1 INTRODUCTION
An omni-directional wheelchair is highly maneu-
verable in narrow or crowded areas such as resi-
dences, offices and hospitals. Several kinds of omni-
directional vehicles have been developed in robotics
fields (West and Asada, 1992), (Pin and Killough,
1994); moreover, some of these have been applied to
wheelchairs (Wada and Asada, 1999), (H.Kitagawa
and K.Terashima, 2004), (Urbano et al., 2005). In
these researches, new mechanism, hierarchical con-
trol and obstacle avoidance of wheelchairs are pro-
posed. However, past researches on the motion con-
trol of omni-directional wheelchairs have not consid-
ered transport wheelchair that is pushed by an atten-
dant. This paper proposes a novel power assist system
for omni-directional transport wheelchairs.
A power assist system of an omni-directional vehi-
cle has been developed in (H. Maeda and Yamashita,
2000). However, it still has some problems in rota-
tion and in rider’s comfort since this system was de-
veloped for a food tray carry vehicle in a hospital.
The purpose of this research is to develop a
power assist system for omni-directional transport
wheelchairs considering attendant’s manipulability
and rider’s comfort. A power assist controller using
vy
vx
v
fx
m
fy
f
Figure 1: Omni-directional wheelchair (OMW)
fuzzy reasoning is proposed to estimate the navigation
direction for the force given by the attendant. Fur-
ther, the second order lag controller which transforms
the force given by the attendant into the velocity of
OMW, is presented to develop the rider’s comfort.
2 OMNI-DIRECTIONAL
WHEELCHAIR
An omni-directional wheelchair (OMW) using omni-
wheels has been designed and built. Figure 1 is an
overview of the OMW. The OMW is able to move in
any arbitrary direction without changing the direction
of the wheels.
211
Urbano J., Terashima K., Nishigaki T., Miyoshi T. and Kitagawa H. (2005).
DEVELOPMENT OF POWER ASSIST ON OMNI-DIRECTIONAL MOBILE WHEELCHAIR CONSIDERING OPERATIONALITY AND COMFORT.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 211-217
DOI: 10.5220/0001172402110217
Copyright
c
 SciTePress

The OMW is equipped with four omni-wheels, and
each wheel has passively driven free rollers at the cir-
cumference. The wheel that rolls perpendicular to the
direction of movement does not stop the movement
because of the passively driven free rollers. These
wheels allow a holonomic omni-directional move-
ment.
6axis force
sensor
1st-order
controller
f
R
directional
reasoning
f
L
f
x
f
y
m
v
x
v
y
d
d
v
y
d
Sensor
input
Sensor
output
Transfer
to velocity
Command input by
direction estimator
Figure 2: Block diagram of power assist system
The OMW is also equipped with a handle and a six-
axis force sensor as shown in Fig.1. Input force to the
handgrips of the handle by the attendant is measured
using the force sensor.
3 POWER ASSIST SYSTEM
3.1 First order controller for power
assist
The first order controller converts the output signal of
the force sensor F =[f
x
, f
y
, m]
T
to the reference
velocity V
omw
=[v
d
x
, v
y
, ω]
T
of the OMW. The input
force can be converted to the reference velocity by
using a controller that contains an integral element.
Moreover, the controller should also have viscosity as
the following equation since the OMW have to stop
safely when F becomes zero.
G
i
(s)=
V
i
(s)
F
i
(s)
=
K
i
T
i
s +1
, (i = x, y, m) (1)
The reference velocity V
omw
exponentially con-
verges to zero by using this controller when the at-
tendant stop pushing the handle. If the time constant
T
i
is too small, the effect of vibration of input force
or noise becomes large. If the time constant T
i
is too
f
y
m
f
x
omw
omw
m
f
x
f
R
f
L
l
f
Ry
f
Rx
f
Ly
f
Lx
O
omw
x
l
y
l
y
f
y
m
f
x
f
y
l
omw
Figure 3: Working force
large, the manipulability of the OMW becomes bad
because of its slow response. In this paper, pareme-
ters were determined as K
x
= 0.0003, K
y
= 0.0002,
K
m
= 0.0007, T
x
= 0.6, T
y
= 0.75 and T
m
= 0.75 by
trial and error.
Table 1: Fuzzy reasoning rules
Rule Antecedent Consequent
1 v
y
> 0 and ω<0 v
d
y
> 0 (Right Slide)
2 v
y
< 0 and ω>0 v
d
y
< 0 (Left Slide)
3 v
y
≈ 0 and ω ≈ 0 v
d
y
≈ 0 (Not Slide)
4 v
y
≥ 0 and ω>0 ω
d
> 0 (CCW Turn)
5 v
y
≤ 0 and ω<0 ω
d
< 0 (CW Turn)
6 v
y
≈ 0 and ω ≈ 0 ω
d
≈ 0 (Not Turn)
Table 2: Parameters of menbership functions
Rule Number
Antecedent
name a b c
1
YPS 7 0.3 -
ONS 7 -0.3 -
2
YNS 7 -0.3 -
OPS 7 0.3 -
3
YZS - - 1000
OZS - - 1000
4
YPT 7 0.3 -
OPT 7 0.3 -
5
YNT 7 -0.3 -
ONT 7 -0.3 -
6
YZT - - 1000
OZT - - 1000
3.2 Direction estimator of navigation
for force input
When the user tries to rotate OMW around its gravity
center, OMW begans to slide and the radius of rota-
tion becomes very big. Then, rotation around the cen-
ter is very difficult. For solving this problem, direc-
tion inference is developed by using the fuzzy rules
shown in Table 1. The block diagram of the system
is shown in Fig. 2. In order to establish the rules
of direction inference, first, the force applied to the
grips of the force sensor are changed to the center of
OMW, as shown in Fig. 3. Note that the input of the
direction estimator is velocity V
omw
, not force F .It
may seem more reasonable to use F for the estimation
of the attendant’s intention, however, it is very diffi-
cult to derive transform equations from F because of
an effect of vibration of input force or noise. v
x
is
not included since forward and backward motion can
be realized without direction estimation. Features of
slide motion is expressed by rules 1 and 2, and that of
ICINCO 2005 - ROBOTICS AND AUTOMATION
212

rotation by rules 4 and 5. Rules 3 and 6 are added not
to generate the reference velocity when input velocity
is zero.
Figure 4 shows the graph of membership functions
of the first rule. The membership function of the an-
tecedent of 1, 2, 4 and 5 is
µ
name
= tan
−1
{a
name
(β
i
− b
name
)} /π+0.5 (2)
where β
i
is input (β
1
= v
y
, β
2
= ω) and a
name
and
b
name
are tuning parameters. ‘name’ is replaced
by the name of each membership function. The
first letter of ‘name’ of antecedents indicates sensor
output(v
d
y
:Y, ω
d
:O), the second letter indicates sign
(Positive:P, Negative:N, Zero:Z), and the third letter
indicates realized motion (Slide:S, Turn:T).
-1 0 1
0
1
-1 0 1
0
1
0
1
0
1
[rad/s]
Antecedent 1
ConsequentAntecedent 2
Rule 1
YPS
ONS
vy [m/s]
y RS
RS
Figure 4: Membership functions of rule 1
The membership function of the antecedent of 3
and 6 is
µ
name
=exp(−c
name
· β
2
i
) (3)
where c
name
is a tuning parameter
3.3 Experimental results
In order to verify the effectiveness of the control sys-
tem, laboratory experiments were conducted. The re-
sults shown correspond to a first order controller. Pa-
rameters of the membership function of Fig. 4 are
shown in Table 2.
The trajectory and velocity v
d
omw
of slide motion
to right are shown in Fig.5 and Fig.6, respectively. As
seen in the trajectory of v
d
y
, vibration of the veloc-
ity was reduced. The trajectory and velocity v
d
omw
of rotation around its center in counter-clockwise are
shown in Fig.7 and Fig.8, respectively. As seen in
Fig.7, the rotation around its center was realized by
using the direction estimator. The effectiveness of the
direction estimator is shown especially in case of ro-
tation.
4 TUNING OF MEMBERSHIP
FUNCTIONS
4.1 Necessity of tuning
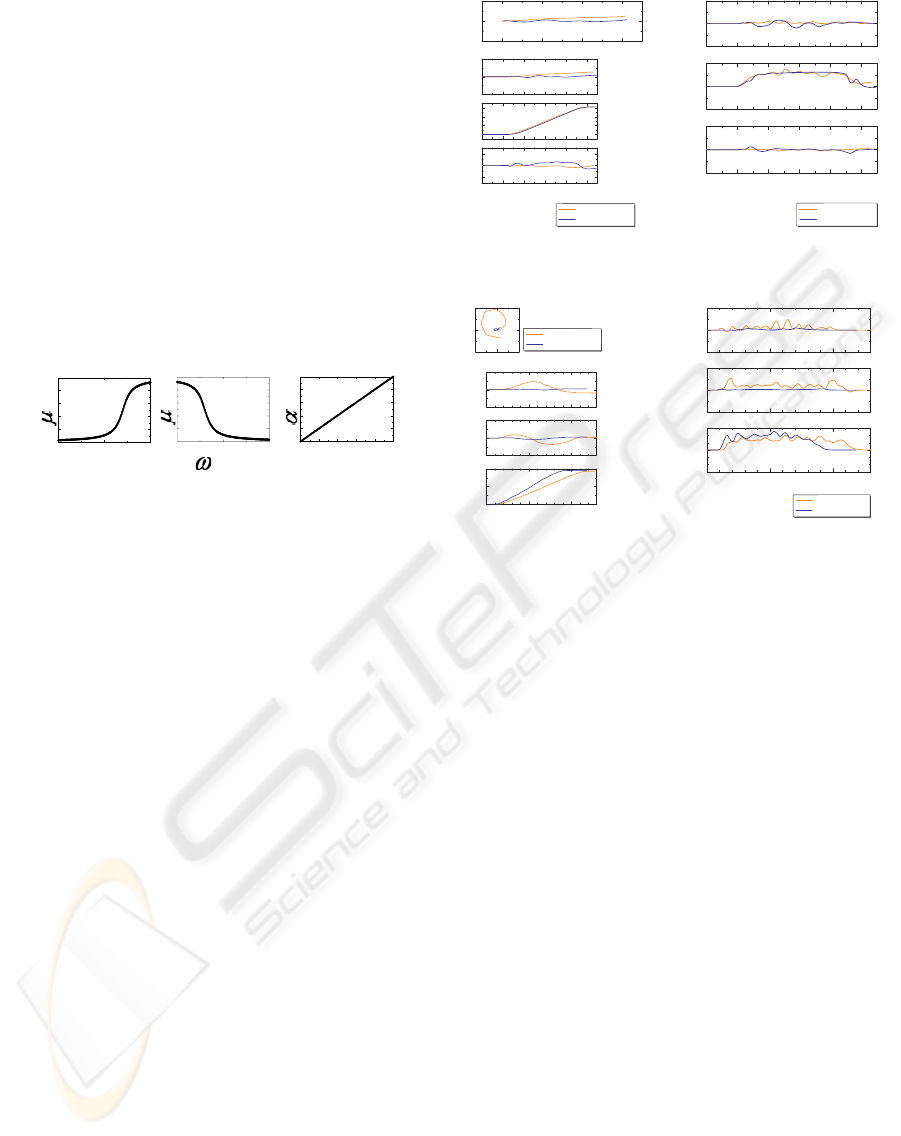
Figure 9 shows the experimental results of using
fuzzy reasoning, where a 60 year-old woman oper-
ated OMW. In Fig. 9, f is a force added by attendant,
0 1 2 3
-1
0
1
y
G
[m]
x
G
[m]
0 2 4 6 8 10
-1
0
1
x
G
[m]
0 2 4 6 8 10
0
1
2
3
y
G
[m]
0 2 4 6 8 10
-10
0
10
θ
G
[deg]
Time [s]
No-reasoned
Reasoned
Figure 5: Trajectory of right
slide
0 2 4 6 8 10
-1
0
1
v
y
d
[m/s]
0 2 4 6 8 10
-1
0
1
ω
d
[rad/s]
Time[s]
0 2 4 6 8 10
-1
0
1
v
x
d
[m/s]
No-reasoned
Reasoned
Figure 6: Velocity v
d
omw
of
right slide
0 5 10
-1
0
1
x
G
[m]
0 5 10
-1
0
1
y
G
[m]
0 5 10
0
200
400
θ
G
[deg]
Time [s]
-0.5 0 0.5
-0.5
0
0.5
y
G
[m]
x
G
[m]
No-reasoned
Reasoned
Figure 7: Trajectory of rota-
tion (CCW)
0 5 10
-1
0
1
v
y
d
[m/s]
0 5 10
-1.5
0
1.5
ω
d
[rad/s]
Time[s]
0 5 10
-1
0
1
v
x
d
[m/s]
No-reasoned
Reasoned
Figure 8: Velocity v
d
omw
of
rotation (CCW)
v
d
is a velocity command, (x
g
, y
g
) is the position of
OMW in the global coordintes and θ
g
is a posture of
OMW.
Here, OMW moves in the following order: For-
ward (1) ⇒ Backwards (2) ⇒ 180
0
Left rotation (3)
⇒ Right slide (4) ⇒ Left slide (5).
Then, Fig. 10 shows the results by fuzzy reason-
ing. Horizontal axis is a translation velocity v
y
before
fuzzy reasoning, vertical axis is a rotational velocity ω
before fuzzy reasoning, darkness degree in the cock-
pit indicator shows the translation velocity v
d
y
and the
rotational command velocity ω
d
after fuzzy reason-
ing, and the real line in Fig. 10 shows the v
y
and
ω operated by attendant in order to get the obtained
movement as shown in Fig. 9
This woman uses the region of v
y
> 0 and ω ≈ 0
while moving towards the right slide. However, while
using the parameter of membership function used in
the previous section, v
d
y
≈ 0.2 [m/s], and ω
d
≈ 0.4
[rad/s] are estimated. Here, this woman intends to
move towards right without rotation, but really moves
towards right with rotation.
Figure 11 shows attendant’s intention representing
direction to make OMW move using v
y
and ω added
by attendant.
In the present fuzzy parameters given by the pre-
vious section, the attendant such as examinee 1 can
operate OMW well.
On the other hand, the attendant such as examinee
2 wants to make OMW move towards right in the re-
DEVELOPMENT OF POWER ASSIST ON OMNI-DIRECTIONAL MOBILE WHEELCHAIR CONSIDERING
OPERATIONALITY AND COMFORT
213

-50
0
50
-50
0
50
-20
-10
0
10
20
0
2468
10 12 14 16 18 20
0
2468
10 12 14 16 18 20
0
2 4 6 8 10 12 14 16 18 20
-25
25
-25
25
-1
-0.5
0
0.5
1
-1
-0.5
0
0.5
1
-1
-0.5
0
0.5
1
0
2468
10 12 14 16 18 20
0
2468
10 12 14 16 18 20
0
2468
10 12 14 16 18 20
0
2468
10 12 14 16 18 20
0
2468
10 12 14 16 18 20
0
2468
10 12 14 16 18 20
-1
-0.5
0
0.5
1
-1
-0.5
0
0.5
1
0
100
200
300
-1
-0.5 0 0.5 1
-1
-0.5
0
0.5
1
(1)
(2) (3) (4)
(5) (1)
(2) (3)
(5)
(4)
v
x
[m/s]
d
v
y
[m/s]
[rad/s]
d
d
f
x
[N]
f
y
[N]
m
[Nm]
t
[s]
t
[s]
t
[s]
y
g
[m]
x
g
[m]
[deg]
x
g
[m]
y
g
[m]
g
(1)
(2)
(5)
(4)
(3)
t
= 4.1[s]
t
= 1.8[s]
t
= 18.0[s]
t
= 15.2[s]
t
= 11.3[s]
Figure 9: Experimental results with fuzzy resoning
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
vy [ m/s ]
[
rad/s
]
vy
[
m/s
]
d
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-1.5
-1.0
-0.5
0
0.5
1.0
1.5
vy [ m/s ]
[
rad/s
]
[
rad/s
]
d
(a) Velocity of slide (b) Velocity of turn
Figure 10: Fuzzy reasoning
gion of v
y
> 0 and ω ≈ 0.
Then, when fuzzy membership function is fixed for
all examinees, the attendant with having the tendency
like examinee 2 feels the difficulty to operate OMW.
Therefore, it is necessary to adjust the parameters of
fuzzy membership functions according to the driving
characteristics of individual persons.
4.2 Tuning system
The parameters in the membership functions are
{a
name
,b
name
,c
name
} as shown in ”(2)” and ”(3)”.
The number of {a
i
,b
i
,c
i
}{i = name} in An-
tecedent part of fuzzy rule is 20. However, the number
of {a
i
,b
i
} is 16, because c
i
doesn’t give a big effect
on the whole result.
Here, a
name
is related with the slope of member-
ship function, while b
name
is with shift quantity in the
movement region. Therefore, the parameter of b
name
is more effective one as the tuning parameter.
Then, eight parameters of b
name
are tunned.
Among them, {b
YPS
,b
YNS
}, {b
YPT
,b
YNT
},
{b
ONS
,b
OP S
} and {b
OP T
,b
ONT
} have the relation
right
slide
ccw
turn
vy
right
slide
ccw
turn
examinee 1
examinee 2
vy
Figure 11: Attendant’s intention
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
d
[
rad/s
]
vy [ m/s ]
vy
[
m/s
]
A
-1.5
-1.0
-0.5
0
0.5
1.0
1.5
d
A
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
[
rad/s
]
vy [ m/s ]
[
rad/s
]
(a) Sampling of feature
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
d
[
rad/s
]
vy [ m/s ]
vy
[
m/s
]
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-1.5
-1.0
-0.5
0
0.5
1.0
1.5
vy [ m/s ]
[
rad/s
]
[
rad/s
]
d
(b) Extension of slide area
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
d
[
rad/s
]
vy [ m/s ]
vy
[
m/s
]
-1.5
-1.0
-0.5
0
0.5
1.0
1.5
d
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
[
rad/s
]
vy [ m/s ]
[
rad/s
]
(c) Reduction of rotate area
Figure 12: Tuning method in the case of slide movement
such as |b
ONS
| and |b
OP S
| is the same, and their sign
is opposite.
Hence, the task for parameter tuning is to determine
four parameters {b
YPS
,b
YPT
,b
ONS
,b
OP T
} and it
is thought to be a comparably easy task.
As a concrete example, let us consider the case of
slide movement. Operator intends to move OMW to-
wards right. Then, moment ω was 0.3 when operator
wished OMW to move towards right.
In this state, the region A is different from operator
intention, because v
d
y
and ω
d
y
are 0, as shown in (a) of
Fig. 12
Thus, the parameters b
name
in Table 2, obtained
by trial and error, must be changed. Then, b
ONS
is
changed from -0.3 to 0.3, and b
OP S
from 0.3 to -0.3,
due to the opposite sign. By this operation, the re-
ICINCO 2005 - ROBOTICS AND AUTOMATION
214

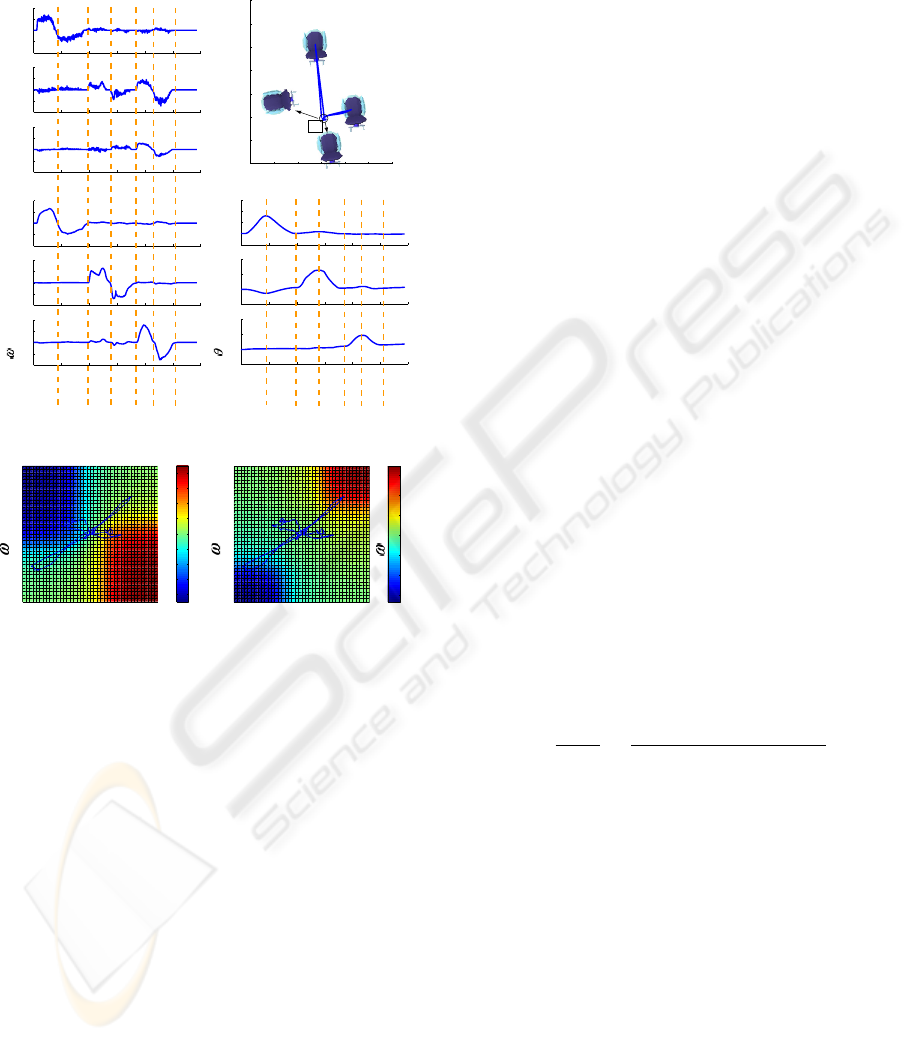
gion of slide is extended, and then it enables OMW to
moves towards right even if ω = 0.3, as shown in the
left figure of Fig. 12 (b).
-1
-0.5
0
0.5
1
-1
-0.5
0
0.5
1
-1
-0.5
0
0.5
1
-60
-30
0
30
60
-60
-30
0
30
60
-30
-15
0
15
30
0 5 10 15 20 25 30
-1
0
1
2
3
-0.5
0
0.5
1
-100
0
100
200
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
0 5 10 15 20 25 30
-1.5
-1 -0.5 0 0.5 1 1.5
-1
-0.5
0
0.5
1
1.5
2
v
x
[m/s]
d
v
y
[m/s]
[rad/s]
d
d
f
x
[N]
f
y
[N]
m
[Nm]
[deg]
x
g
[m]
y
g
[m]
g
t
[s]
y
g
[m]
x
g
[m]
t
[s]
t
[s]
(1)
(2) (3) (4)
(5)
(6)
(1)
(2) (3) (4)
(5)
(6)
2.5
(1)
(2)
(3)
(4)
(5)
(6)
t
= 4.5[s]
t
= 25.8[s]
t
= 21.3[s]
t
= 14.0[s]
Figure 13: Experimental results with fuzzy resoning
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
d
[
rad/s
]
vy [ m/s ]
vy
[
m/s
]
-1.5
-1.0
-0.5
0
0.5
1.0
1.5
d
-1.0 -0.5 0 0.5 1.0
-2.0
-1.0
0
1.0
2.0
[
rad/s
]
vy [ m/s ]
[
rad/s
]
(a) Velocity of slide (b) Velocity of turn
Figure 14: Fuzzy reasoning after tuning
However, ω
d
will generate in the region A, when ω
= 0.3 is used. Then, OMW will simultaneously rotate
with right slide.
In order to avoid this, b
OP T
is changed from 0.3 to
0.9, and b
ONT
from -0.3 to -0.9. Then, as seen from
the right figure of Fig. 12 (c), ω
d
doesn’t generate
in the region A, and therefore OMW moves towards
right slide without rotation.
Following this procedure, parameter tuning can be
realized by easy manner. A monitor system has been
developed such as the result of fuzzy reasoning like
Fig. 12, and position and posture of OMW in the
global coordinate, can be pictured in real time.
Figure 13 and Fig 14 show the experimental results
after tuning for this person. Tuning was conducted
such that right slide could be done under the condi-
tions of v
y
> 0 and ω ≈ 0. OMW was moved in the
order:
Forward ⇒ Right slide ⇒ Left slide ⇒ 90
0
right
turn ⇒ 90
0
left turn
She uses the region of ω = 0, when she wants OMW
to conduct the slide motion. Then, the required move-
ment was realized by tuning. Thus, the improvement
of operation was achieved.
5 IMPROVEMENT OF COMFORT
BY USING A SECOND ORDER
CONTROLLER
When the first order controller in previous section is
used according to previous research, a big jerk (varia-
tion of acceleration) appears if the input force changes
suddenly. Jerk is considered as the factor that dom-
inates riding comfort. For riding comfort improve-
ment, jerk must be decreased. A method for decreas-
ing jerk is proposed as follows:
i) Decrease the gain K
i
,(i = x, y, ω).
ii) Increase the value of the time constant T
i
,
(i = x, y, ω).
iii) Establish the largest restriction of jerk.
iv) Modify the controller.
In item (i), as the output velocity related to the help
force becomes smaller, the jerk becomes small too.
However, a big force is necessary for achieving the
desired velocity. Then, the effect of power assist fades
and OMW becomes, once again, very heavy for the
attendant.
In items (ii) and (iii), jerk can be made smaller too,
but in this case, after the change, the time for reaching
the desired velocity increases. This generates a prob-
lem of deterioration of operability. In brief, with the
proposed method is possible to improve riding com-
fort, but operability of OMW decays. Then, a second
order controller
G
i
(s)=
V
i
(s)
F
i
(s)
=
K(ω
n
)
2
i
s
2
+2ζ
i
(ω
n
)
i
s +(ω
n
)
2
i
, (4)
(i = x, y, m)
is chosen as a power assist controller which can pro-
vide compatibility for both operability and riding
comfort. Here, ζ is the attenuation factor. Even when
the help force is fix, if overshoot O
s
occurs, certain
amount of time is required for the velocity to con-
verge and operability deteriorates. Then, in order to
avoid overshoot ζ
i
is chosen as ζ
x
=1,ζ
y
=1,ζ
m
=1.
In addition, for the resonant frequency ω
n
, in the
case when the time constant of the first order con-
troller T
x
= 0.4, T
y
= 0.4 and T
m
= 0.4, is used, it
makes difficult for ω
n
to be influenced by the noise
included in the help force and as a consequence good
operability of OMW is obtained. Then, in this case
and in order for recovery time to become the same,
ω
n
) is chosen, by trial and error, as (ω
n
)
x
=4,(ω
n
)
y
=4,(ω
n
)
m
=4.
DEVELOPMENT OF POWER ASSIST ON OMNI-DIRECTIONAL MOBILE WHEELCHAIR CONSIDERING
OPERATIONALITY AND COMFORT
215

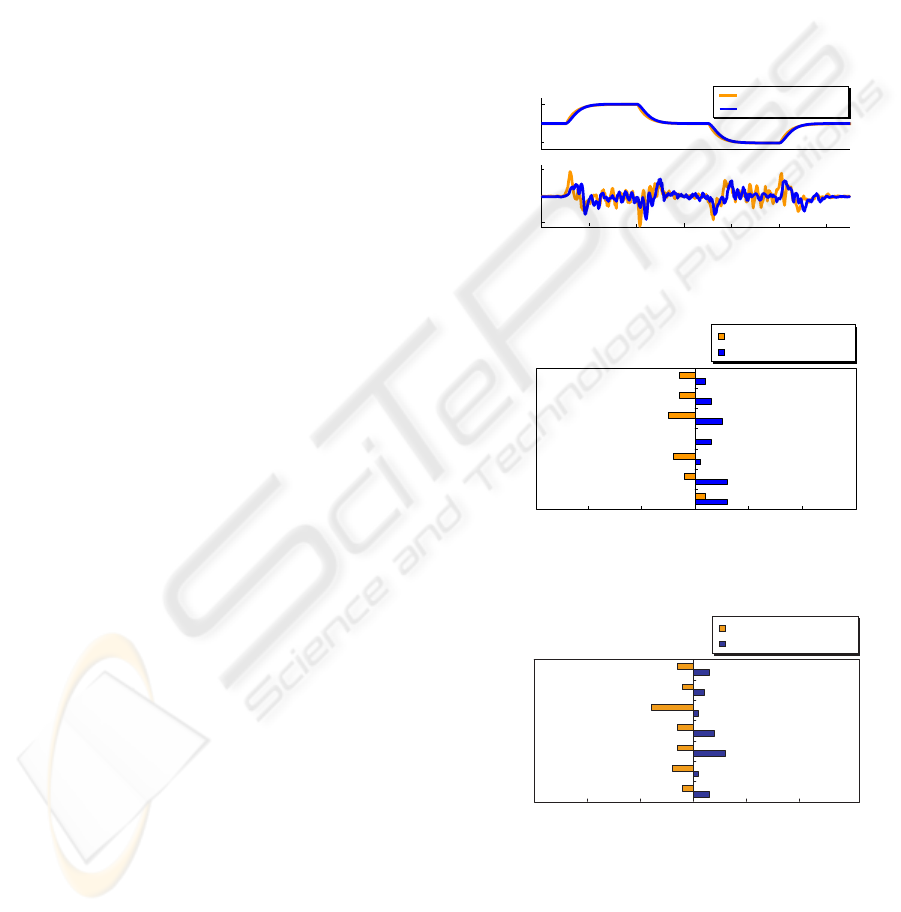
Experimental comparison of the jerk produced in x
direction by a first order controller and a second or-
der controller, for the same reference velocity, was
conducted. The experimental parameters were: K
x
=
0.02CT
x
= 0.4Cζ
x
= 1.0C(ω
n
)
x
= 4.0Csampling time
t
s
= 0.03[s]. OMW was moved in automatic mode
with an input help force given as:
f
x
=

0(0≤ t<1, 4 ≤ t<7,t≥ 10)
50 (1 ≤ t<4)
−50 (7 ≤ t<10)
Jerk was evaluated by differentiating the output of
the encoders of OMW’s motors. Experimental results
are shown in Fig. 15. v
x
is the reference velocity,
j
omw
x
shows the actual jerk that was calculated by us-
ing the encoders output. As in order to calculate the
jerk from the encoders output it is necessary to dif-
ferentiate the encoders output, there is the problem
that even a little noise present in the encoders out-
put will cause big changes in the value of jerk due
to differentiations. Here, instead of concentrating in
very precise values of jerk, attention is given to the
big variations of jerk, so using values of jerk for (t-1)
and (t+1), where t is the actual time, a moving aver-
age of jerk is calculated. As the velocity is constant
between t=3‘4[s], the jerk observed in this interval of
time is due to the erratic reading of encoders and then
is ignored. Attention will be focused on the interval of
time between t=1‘2[s], in which there is acceleration
and deceleration. It has been verified that a second
order controller can achieve a maximum reduction of
20% of the value of jerk produced during this period.
Then, improvement of riding comfort is assured by
using a second order controller. Moreover, compar-
ing this results with the case in which the reference
velocity is input to a first order controller, there is al-
most no delay of time response and then operability
is not degraded. For these reasons, it is possible to
conclude that in this case second order controller has
a better performance than first order controller.
In addition, as riding comfort is something that de-
pends on the subjective judgement of the OMW’s oc-
cupant, riding comfort was evaluated by using Se-
mantic Differential (SD) method.
OMW was made to move in automatic mode in
x direction and y direction and a questionnaire con-
sisting of 7 items related to driving comfort was pre-
sented to 10 different people. The mean value of the
results obtained in each item are shown in Fig. 16 for
x direction and Fig. 17 for y direction. Even when the
difference for the results in x direction and y direction
is not so big, it is possible to see that the values ob-
tained by the second order controller are much better
than that obtained by the first order controller. Then
a second order controller will be used as power assist
controller because it can improve riding comfort.
6 CONCLUSIONS
A power assist system for omni-directional transport
wheelchairs considering both attendant’s manipula-
bility and rider’s comfort was developed. The refer-
ence velocity of the omni-directional wheelchair was
derived from attendant’s input force. Manipulability
of rotation was improved greatly by using the fuzzy
direction estimator.
In order to improve riding comfort, the first order
controller has been changed by newly giving a second
order controller which can improve the riding comfort
for reducing the jerk. Comfort has been enhaced by
using a second order controller.
024681012
1st-order controller
2nd-order controller
t [s]
-5
0
5
j
x
[
m/s
]
3
omw
024681012
-1
0
1
vx
[
m/s
]
jerk
velocity
time
Figure 15: Experimental result of jerk
-2 -1 0 1 2
point
1st-order controller
2nd-order controller
3-3
swing
feeling
security
comfort
stability
reliability
ride quality
Figure 16: Questionnaire result of x-axis
-2 -1 0 1 2
point
1st-order controller
2nd-order controller
3-3
swing
feeling
security
comfort
stability
reliability
ride quality
Figure 17: Questionnaire result of y-axis
ACKNOWLEDGMENTS
This work was partially supported by The 21st Cen-
tury COE Program ”Intelligent Human Sensing”
ICINCO 2005 - ROBOTICS AND AUTOMATION
216

REFERENCES
H. Maeda, S. Fujiwara, H. K. and Yamashita, H. (2000).
Development of omni-directional cart with power as-
sist system (in japanese). In Proc. 18th Annual Conf.
of Robotics Society of Japan, 15, pp.1155-1156.
H.Kitagawa, T.Nishigaki, T. and K.Terashima (2004).
Fuzzy power assist control system for omni-
directional transport wheelchair. In Proc. IEEE/RSJ
Int. Conf. on Intelligent Robots and SystemsC1580-
1585.
Pin, F. and Killough, S. (1994). A new family of omni-
directional and holonomic wheeled platforms for mo-
bile robots. In IEEE Trans. Robot. Automat., pp. 480-
489.
Urbano, J., Yang, Y., Terashima, K., Miyoshi, T., and Kita-
gawa, H. (2005). Navigation with comfort of omni-
directional wheelchair driven by joystick. In Proc.
IFAC World Congress, (to be published).
Wada, M. and Asada, H. (1999). Design and control of a
variable footprint mechanism for holonomic omnidi-
rectional vehicles and its application to wheelchairs.
In Proc. IEEE Trans. Robot. Automat, 15, pp. 978-
989.
West, M. and Asada, H. (1992). Design of a holonomic om-
nidirectional vehicle. In Proc. IEEE Int. Conf. Robot.
Automat., pp. 97-103.
DEVELOPMENT OF POWER ASSIST ON OMNI-DIRECTIONAL MOBILE WHEELCHAIR CONSIDERING
OPERATIONALITY AND COMFORT
217