FUZZY ADAPTIVE CONTROLLER FOR A SYNCHRONOUS
MACHINE
Gregorio Drayer and Miguel Strefezza
Departamento de Procesos y Sistemas, Universidad Simón Bolívar, Caracas 1081A, Venezuela
Keywords: Fuzzy control, Adaptive rules, Variable Structure Control, Synchronous machine.
Abstract: This paper presents the comparison of applying an adaptive fuzzy controller with and without a variable
structure controller (VSC) for a synchronous machine. A simplified linear model of the synchronous
machine connected to an infinite bus with constant impedance is used. The multivariable system was
previously decoupled to make easier the application of the control schemes. To control the system, an
adaptive Fuzzy PD controller is proposed and it acts both on the load variable and on the voltage variable.
Then, a Fuzzy Adaptive System is designed to act over the Fuzzy controller. After this, the VSC theory is
applied to the Adaptive Controller to compare both strategies. Simulation results using these two control
schemes are presented. With these proposed actions, the results show a better transitory response of the
system when compared with the system response using classical control.
1 INTRODUCTION
The need of energy increases every year, specially in
industrially developed countries. Very complex
systems have been designed and operated to supply
the energy demand. These systems are networks of
generators and loads connected by transmission lines
that present many engineering problems with a
variety of challenges. Synchronous machines are
designed to feed the loads at constant frequency and
voltage. Any unbalance between generation and load
initiates a transient that can cause instabilities
because of the net accelerating torques exerted on
the rotors. Classical PID controllers can not deal
effectively with many of the problems. Thus, a
possible solution could be the application of non-
linear controllers (
Vidyasagar,1993). Under perfect
knowledge of the process and its disturbances, the
nonlinear approach can provide good performances
in a wide range of values.
The control of the synchronous machine can be
designed by using the knowledge of the operators.
Fuzzy controller design is based on converting
linguistics control strategies obtained from an
expert’s knowledge or from the input-output data of
a process (Takagi and Sugeno, 1985). Then, the
control algorithm can described by fuzzy rules of the
form If-Then. One of the relevant advantages of
fuzzy controller is the absence of necessity for an
analytical description of the process to be designed
or implanted. Also, it can be implemented more
easily. Its applications to different processes have
been presented (Jang, Sun and Mizutani,1997)
(Yager and Filev, 1994), but very few applications
to synchronous machine systems can be found where
this methodology is used.
PID controllers are frequently used in the
industry. They have many advantages, but they are
difficult to be tuned when a process has to be
working in different set points or in a wide range. A
multivariable model of the synchronous machine is
used in this work. After the variables are decoupled,
the main goal is to present the application of a Fuzzy
Controller with fuzzy adaptive rules. Then, a fuzzy
sliding controller is added to the overall adaptive
fuzzy control for the load variable of a synchronous
machine. The purpose is to compare the advantages
of both controllers (
Huang and Lin, 2003) (Li and
Gatland, 1997).
Simulations are carried out, showing that the
proposed strategies present good results. The
description of the system is presented in section 2.
The control strategy is outlined in section 3, the
results of simulations based on the outlined model
are showed in section 4. Finally, in section 5 the
conclusions are given and recommendations are
proposed.
210
Drayer G. and Strefezza M. (2005).
FUZZY ADAPTIVE CONTROLLER FOR A SYNCHRONOUS MACHINE.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 210-215
DOI: 10.5220/0001172702100215
Copyright
c
 SciTePress

2 MODEL OF THE SYSTEM
In this section the mathematical model describing
the dynamic behavior of the synchronous machine is
presented (
Anderson, 1993) where state-space
formulation of the machine equations is used.
In this study a simplified linear model of a
synchronous machine connected to an infinite bus
through a transmission line of resistance R
e
and
inductance L
e
is used. In the selected model the
following assumptions are made:
- The effects of the amortisseur are neglected.
- The resistance of the stator winding is neglected.
- The terms
qd
λλ

,
in the stator and load voltage
equations are neglected compared with the terms of
speed voltage
qd
ωλ
ωλ
,
.
- The terms
ωλ
in the stator and load voltage
equations are supposed to be approximately similar
to
λ
ω
R
.
- It is supposed a balanced system without saturation
effects.
Then, the equations of the system are given by:
∆FD∆q∆q∆
d
δKKEKEEτK
433
0
3
−=
′
+
′′

∆∆∆
′
+=
qe
EKKT
21
δ
∆∆∆
′
+=
qt
EKKV
65
δ
(1)
∆∆∆
−=
emj
TT
ω
τ

∆∆
= ωδ

By eliminating V
t ∆
and T
e∆
of (1) it is obtained:
∆∆∆∆
′
+
′
−
′′
−=
′
FDddqdq
EKEKE )/1()/()/1(
00403
τδττ

(2)
∆∆
= ωδ

Taking the state variables E'
q∆
, ω
∆
and δ
∆
, the
input signals as E
FD∆
and T
m∆
. Equation (2) is
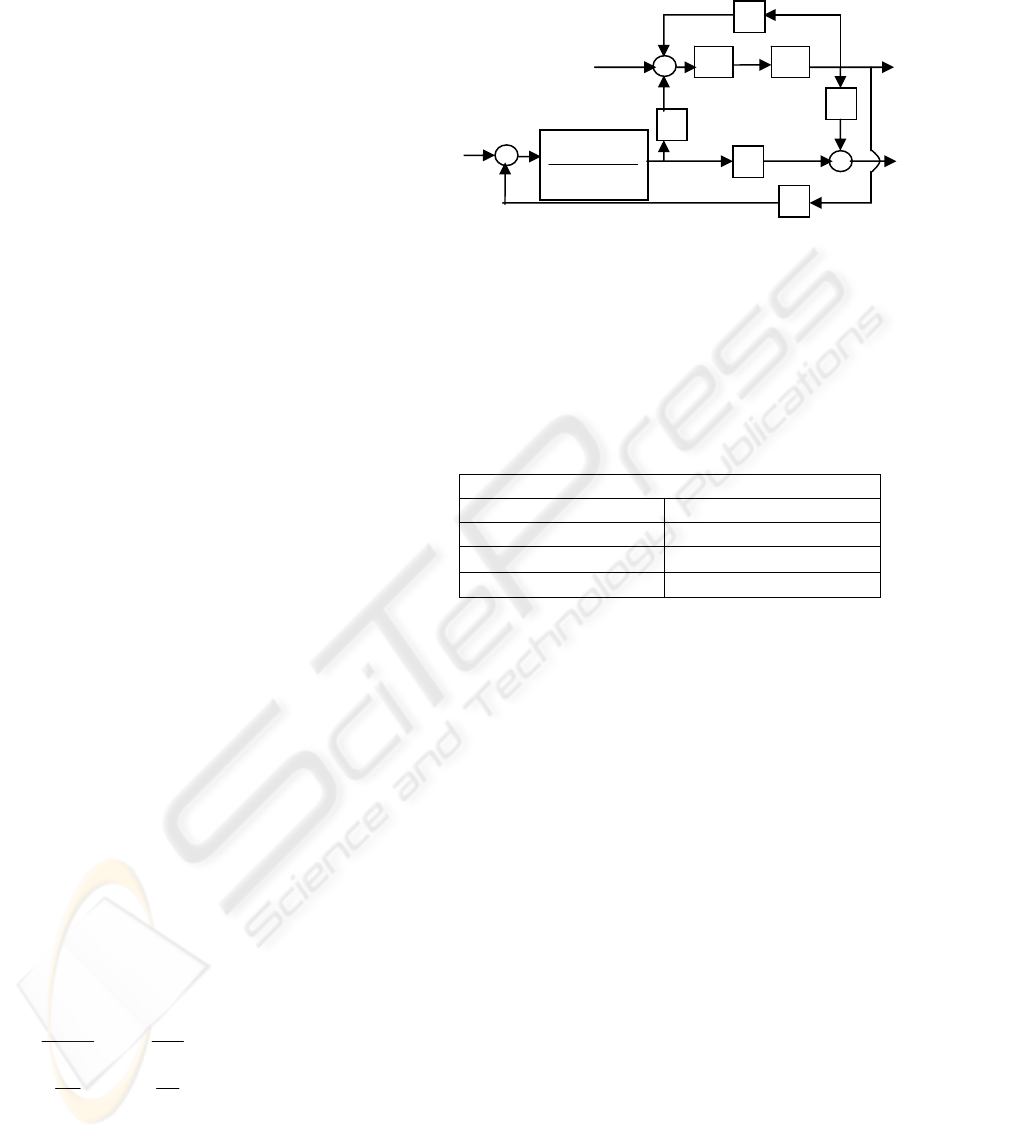
written in state-space (3). In figure 1 the block
diagram (
Anderson, 1993) shown describes the
synchronous machine connected to an infinite bus
through a transmission line. In this diagram the
subscript
∆ was omitted for convenience.
(3)
Figure 1: Block diagram of the simplified linear model of
a synchronous machine
Assuming
ω
R
= 377 rad/s, R
e
= 0.02 pu (per unit),
L
e
= 0.40 pu, V
a
= 1 pu, V = 0.828 pu, cos (φ) = 0.85,
x
d
=1.7 pu, x
q
= 1.64 pu, x'
d
= 0.245 pu, the
parameters of the system are presented in Table 1.
Table 1: Constant and parameters of synchronous machine
model
Constant and parameters
K
1
= 0.7598 K
5
= -0.0409
K
2
= 1.2578 K
6
= 0.4971
K
3
= 0.3072
τ ’
d0
= 5.6
K
4
= 1.7124
τ
j
= 1658.8
3 EXPERIMENTAL PROCEDURE
3.1 Decoupling of the variables
Firstly, K is calculated according to the control law
(4) to obtain a stable system. Subsequently a
decoupling net is designed. By using (4), the
matrixes Ni and M are determined, describing the
system in equation (5). This tool uses a decoupling
net that converts the MIMO system problem in a
number of SISO system problems.
(4)
(5)
The system can be written as equation (6).
(6)
With the controlled variable being
+
E
FD ∆
_
K
1
1/
τ
j
s ω
∆
/s
K
2
K
5
K
6
K
4
sK
K
d 03
3
1 τ
′
+
_
T
m ∆
+
_
δ
∆
V
t ∆
+
+
x
KK
y
ux
KK
K
K
x
j
d
jj
dd
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−
−−
=
56
0
12
0
4
03
1
0
0
0
0
/1
0
0
0
'/1
010
0
'
0
'
1
τ
τ
ττ
ττ

)(
ˆ
BKAA −=
Cxy
BNivxNiMBKAx
=
+
−
−
=
)(

[]
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⋅⋅−
⋅⋅⋅−⋅−
=
⎥
⎦
⎤
⎢
⎣
⎡
c
cccc
c
c
x
x
Cy
r
Bx
x
ACHB
CNiBMNiKBA
x
x
0
0


∆∆∆∆
+−
′
−=
mjjqj
TKEK )/1()/()/(
12
τδττω

FUZZY ADAPTIVE CONTROLLER FOR A SYNCHRONOUS MACHINE
211

decoupled, it is possible to design a SISO controller
for each one.
In this work the main objective is to introduce a
hybrid controller for the load variable. To control the
voltage variable a PD like fuzzy controller is used.
3.2 Design of the PID controller
In figure 2 the diagram of the multivariable control
is shown. .
The PID controller was adjusted by using the
Ziegler-Nichols tuning rules method and then the
system responses satisfactorily to a step input. The
values obtained to adjust the controller are shown in
table 2.
Table 2: Value of the PID controller constant obtained
with the Ziegler-Nichols method.
Kp
ZN
Ki
ZN
Kd
ZN
0,0004 1,0E-9 0,02
3.3 PD like fuzzy controller
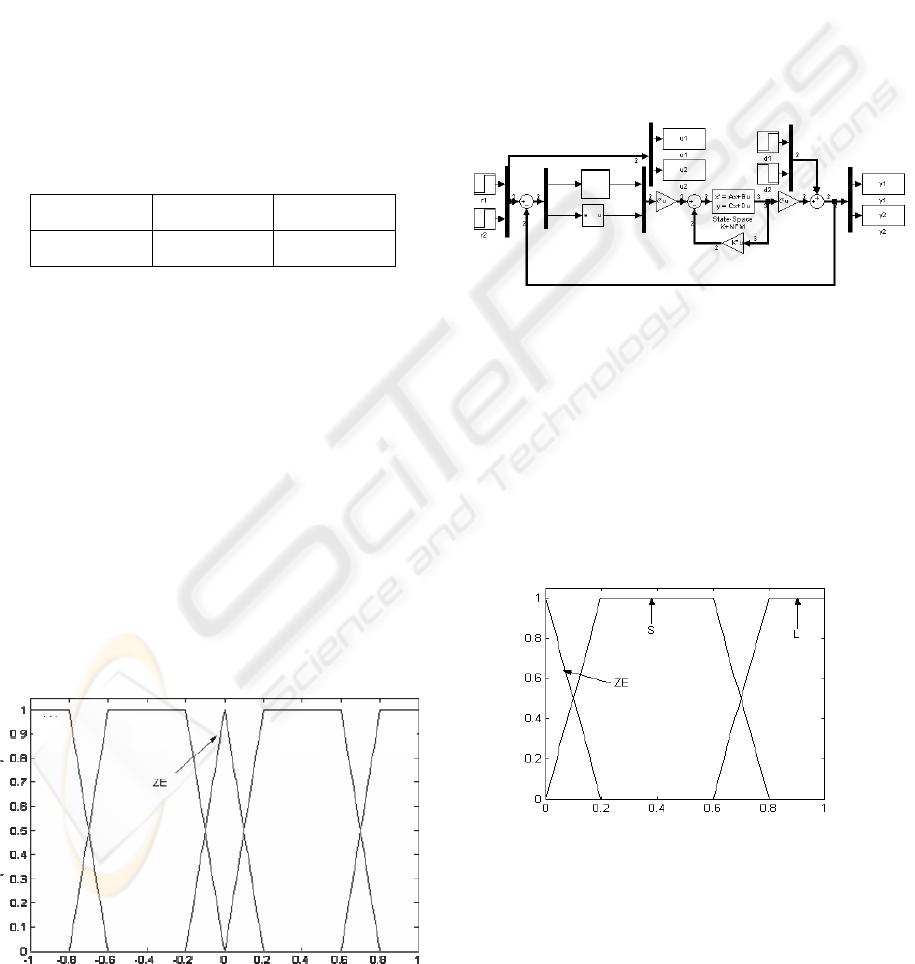
The fuzzy controller was designed using trapezoidal
membership functions. The universe of discourse
consists of five fuzzy values:
1. PL: positive large.
2. PS: positive small.
3. ZE: zero.
4. NS: negative small.
5. NL: negative large.
Figure 2 shows the universe of discourse and the
membership functions.
Furthermore, the following control rules (
Li and
Lau, 1988)
were used with the previously presented
membership functions:
Figure 2: Universe of discourse and membership function
1. if e’ is PL and ∆e’ is any, then u is PL.
2. if e’ is PS and
∆e’ is PS or ZE, then u is PS.
3. if e’ is ZE and
∆e’ is PS, then u is ZE.
4. if e’ is ZE and
∆e’ is NS, then u is NS.
5. if e’ is NS and
∆e’ is NS, then u is NS.
6. if e’ is PL and
∆e’ is any, then u is NL.
The fuzzy controller uses Mamdani (max-min)
defuzzification. The controller works on the load
variable of the system. Figure 3 shows the block
diagram of the overall control system. It can be
noticed that the decoupling artifice for the variables
has been included in the system model. It can be
also observed that a PD like fuzzy controller is used
for the load and for the voltage.
Figure 3: Decoupled control system with a fuzzy
controller for the load and for the voltage
3.4 The adaptive fuzzy rules
To adjust the employed fuzzy controller an adaptive
fuzzy law is implemented, the membership functions
are showed in figure 4.
Then to adjust the parameter Kp of the fuzzy
controller the following relations are used:
Kp=FKp.Kp
ZN
Figure 4: Universe of discourse and membership function
for the adaptive law
The rules used are:
If
|e| is L then FKp is 1.7
If
|e| is S then FKp is 1.7
If
|e| is ZE then FKp is 1
NL
NS PS PL
Load Fuzzy Controller
Voltage Fuzzy Controller
Ni
C
e u
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
212

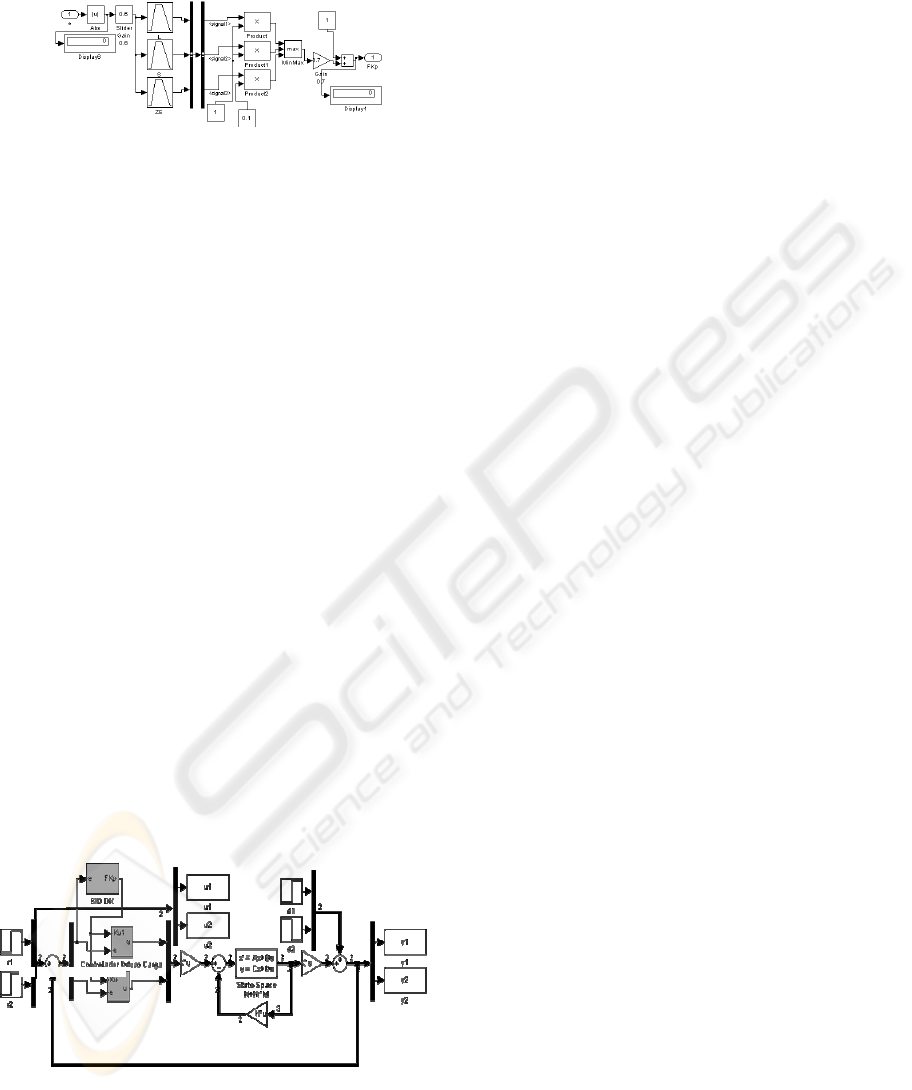
Figure 5 shows the inference system that allows
generating the variations of FKp.
Figure 5: System to generate variations of FKp
3.5 Adaptive Fuzzy Sliding Control
The methodology used here is proposed in (Li and
Gatland, 1997)
to improve the fuzzy controller. The
switching line is formed by a hierarchical method
given by:
221
112
1
−−−
+=
+=
+=
nnn
ee
σλσσ
σλσσ
λσ

#


(7)
In this case the output of the sliding surface
variable is used as the input of the adaptive
controller.
3.6 Implanting the adaptive
controller to the synchronous
machine system
When all the necessary subsystems, such as the
fuzzy controller, the PID controller are designed and
the outlined scheme of control is defined, the
following step is to integrate all these in the control
system to solve the problem.
Figure 6 shows the block diagram of the system
of final control system. It can be noticed that the
action of fuzzy controller will work together to
control the load.
Figure 6: Adaptive Fuzzy Controller
4 RESULTS AND DISCUSSION
In this section simulations are presented and the
analysis of the results obtained from the control
scheme proposed in this work. With this system
simulations were carried out having a step input
signal of 0.8 p.u. of magnitude at 100 s after the start
point. The responses of the system with and without
the fuzzy variable structure controller and other
control strategies are presented.
4.1 Comparison of the adaptive
fuzzy controller with other
controllers
The results of the tests carried out with the Adaptive
PD Like Fuzzy Controller are shown in different
detail in figures 7, 8 and 9. It can be observed in
figure 7 that the PID controllers have a larger
settling time than the PD controllers. The PID
controllers reach a stationary state between 100 s
and 450 s after the input reference is introduced. On
the other hand, the PD Like Fuzzy controllers
achieves smaller rise time to about 50 s after the
input. Among the PID controllers, the fuzzy
controller shows the best effectiveness. This
controller is able to follow the reference with a delay
of about 100 s without overshoot. The classic PID
controllers present overshoot.
In figure 8 a more detail the comparison among
the controllers is shown. In this detail, it can be
observed that the PD like fuzzy controller has a
better response-time and settling time than all the
PID controllers. Inclusive, they show zero steady
state error. Also, the PD like fuzzy controllers
stabilize in about 20 s, while the quickest for the PID
controllers is 100 s. The fast behavior in the PD on
top of the PID is due to the predominant action of
the proportional and derivative factors of the
controllers; they react to the changes in the error.
Making another comparison between these
controllers, in figure 9 the PD like fuzzy controller
and adaptive PD like fuzzy controller can be
compared. In this figure an even faster settling time
is reached: less than 20 s, without overshoot. In
general, the adaptive controller is better than the PD
like fuzzy controller. In the transitory response the
adaptive fuzzy controller is able to overcome in 5 s
the fuzzy controller. This figure also shows that the
adaptive fuzzy controller responds even quicker that
all the controllers previously mentioned
With these results obtained, the theory of
variable structure control was applied to compare it
with the best controllers obtained.
Ni
C
Voltage Fuzzy Controller
FIS DK
Load Fuzzy Controller
FUZZY ADAPTIVE CONTROLLER FOR A SYNCHRONOUS MACHINE
213

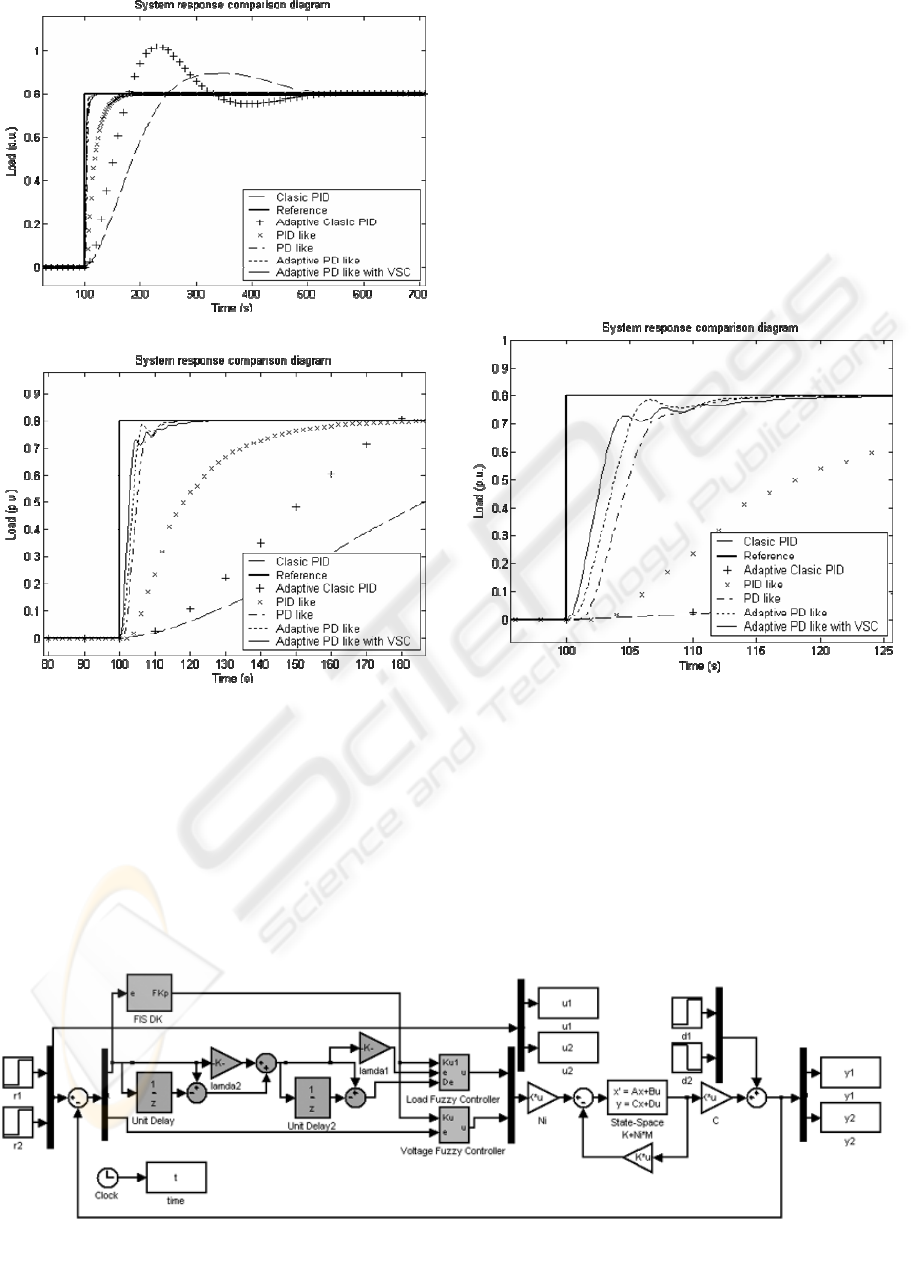
Figure 10: Fuzzy VSC Scheme
Figure 7: System response comparison
Figure 8: Detail of the transitory system responses
4.2 The adaptive PD like fuzzy
controller with and without the
VSC and their comparison with
the PD like fuzzy controller
The results obtained in this section are essential in
this work. In figure 10 the application of the theory
of variable structure control (VSC) to an adaptive
fuzzy controller is showed. In this figure, the PD
like fuzzy controller responses also presented to
establish comparison points illustrate the
effectiveness of the system with VSC.
In can be noticed in figure 11 that the settling
time of the controller with VSC is about 25 s while
the other controllers is less than 20 s. From this point
of view, the PD controllers without VSC are
superior. Looking at the controllers’ response, that
with the VSC reacts more quickly than the others,
achieving an advantage of a little more than 1 s.
Then, according to the results, by applying these
controllers in particular to this system, it can be
appreciated a compromise between the speed
response and the settling times of these controllers.
Figure 9: Adaptive Controller and others
The action of the fuzzy controller is remarkable.
The behavior of the system corresponds to the
requirements of the designer, allowing interesting
results for the transient. It can be observed that the
action of system with any of the fuzzy controller
suppresses any overshoot produced by using a
classical PID controller, overcoming its
effectiveness during the transient response.
In Figure 12 the response of the system with
load change is showed and Figure 13 presents a
detail
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
214

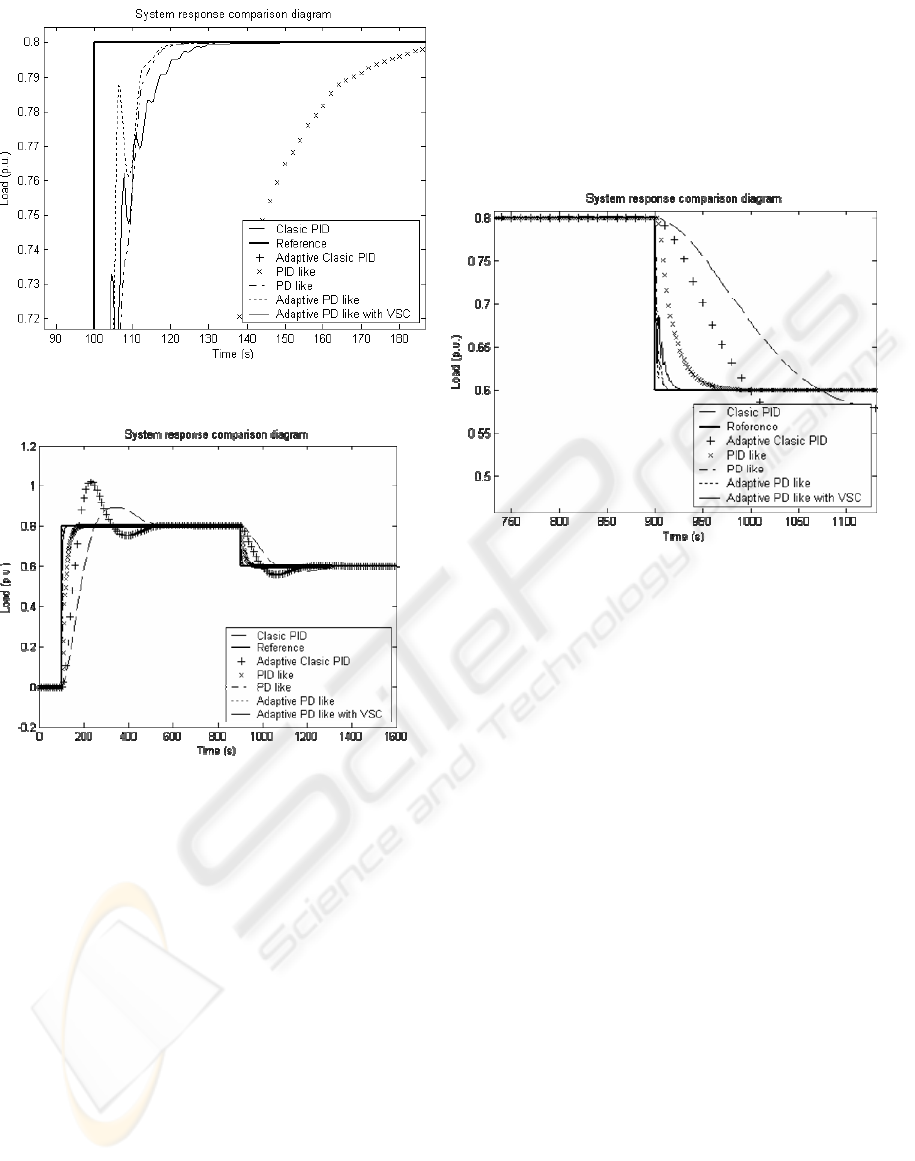
Figure 11: Adaptive and VSC Fuzzy Controller
comparison
Figure 12: Response of the system to load change for
different control schemes
5 CONCLUSIONS
The model used for the synchronous machine can be
decoupled allowing the separate study for each one
of its controlled variables. The response of the
system with the outlined fuzzy adaptive controller is
superior to any other scheme used to control the
synchronous machine. The combination of both
techniques also allows a spectrum of possibilities to
perform control actions on the controlled variable of
the system. The number of rules and the universe of
discourse used to define the fuzzy inference system
is very simple and small which allow an easy
implementation. The use of oriented object
programming helps to make the controller design a
more simple process. The design of these control
schemes with or without the VSC for the system
enhances the capacities and potentials of achieving
physical realizations that show a high level of
autonomy and flexibility. The use of a fuzzy
technique to control synchronous machine is
recommended due the satisfactory results obtained
in these experiences.
Figure 13: Detail of the load change response of the
system for different schemes
REFERENCES
Anderson, P., 1993. Power System Control and Stability.
IEEE Power Systems Engineering Series.
Huang, S-J and Lin, W-Ch., 2003. Adaptive Fuzzy
Controller with Sliding Surface for Vehicle
Suspension Control. IEEE Transaction on Fuzzy Syste,
Vol. 11, No. 4 August.
Jang J-S., C-T. Sun and Mizutani, E.,1997. “Neuro-Fuzzy
and Soft Computing”, Prentice Hall.
Li, H.X. and Gatland, H.B., 1997. Fuzzy Variable
Structure Control. IEEE Transactions on system, man,
and cybernetics Part B. Vol. 27, No. 2, April.
Li, Y.F. and Lau, C.C., 1988. Development of Fuzzy
Algorithms for Servo Systems. IEEE International
Conference on Robotics and Automation,
Philadelphia, Pennsylvania, April, 24- 29, 1988.
Takagi T. and Sugeno M., 1985. Fuzzy Identificacion
of Systems and its applications to Modelling Control.
IEEE Trans. on System, man and Cybernetics, V.
SMC-15, pp. 116-132.
Vidyasagar M., 1993. “Nonlinear System Analysis”.
Prentice Hall Inc.
Yager R.R. and Filev D.P., 1994. “Essentials of Fuzzy
Modeling and Control”. Wiley & Son, Inc.
FUZZY ADAPTIVE CONTROLLER FOR A SYNCHRONOUS MACHINE
215