ACOUSTIC NOISE SUPPRESSION: COMPROMISES IN

IDENTIFICATION AND CONTROL

Ricardo S. S

anchez Pe

na, Miquel A. Cuguer

o, Albert Masip, Joseba Quevedo, Vicenc¸ Puig

Sistemas Avanzados de Control, ESAII, Universidad Polit

ecnica de Catalunya,

Rambla Sant Nebridi 10, Terrassa, Barcelona, Espa

Keywords:

Active acoustic noise suppression, robust identiﬁcation, H

∞

control, µ–analysis.

Abstract:

The objective of this work is to explicitly point out the compromises in the identiﬁcation and control stages

in an acoustic noise suppression experiment, in terms of performance vs. controller order. The identiﬁcation

is a control–oriented robust procedure which takes into account both, parametric and non–parametric models,

and is applied to the primary and secondary circuits of an acoustic tube. The control is designed via the H

∞

optimal control theory, and the analysis of the closed loop system is performed via the structured singular

value (µ).

1 INTRODUCTION

Uncertainty in models which describe physical sys-

tems has deserved a great deal of attention. Robust

Control and Identiﬁcation techniques have worked

with this hypothesis in the ’80s and ’90s respectively.

Uncertainty has been considered both as unstructured

(or global dynamic) and structured (either parametric

or dynamic). Control design techniques are quite dif-

ferent in both cases. Parametric analysis and design is

known to be an NP-hard problem (Braatz. et al., 1994;

Puig et al., 2003). Instead for global or structured

dynamic uncertainty optimal control methods can be

used as the well known H

∞

control and µ–synthesis,

respectively.

The area of Control oriented Identiﬁcation seeks

either a frequency domain or time domain unstruc-

tured uncertainty family of models from a determinis-

tic worst case viewpoint (Chen and Gu, 2000), Chap

9 of (S

anchez Pe

na and Sznaier, 1998). Further re-

search led to combinations of time and frequency do-

main measurements (Parrilo et al., 1998) as well as

parametric and non–parametric models (Parrilo et al.,

1999).

Here we will use some results from the Robust

Identiﬁcation area which combines parametric and

dynamic models (Parrilo et al., 1999; Baldelli et al.,

2001; Mazzaro et al., 2004) to obtain a global dy-

namic uncertain set describing the physical plant. In

particular, interpolation results based on the general

interpolation theory in (Ball et al., 1990) are applied,

which potentially can combine both type of exper-

imental data: frequency and time domain measure-

ments (Parrilo et al., 1998).

The main objective of this work is to explicitly

point out the compromises which arise in the iden-

tiﬁcation and controller design stages of a particu-

lar problem. The application example is an acoustic

noise suppression problem, which combines several

characteristics of many other general problems: well

deﬁned parametric components, dynamic uncertainty,

measurement noise, right half plane zeros feedfor-

ward and feedback control (Fang et al., 2004). This

can be found in many other applications in the areas

of civil, mechanical, aeronautics and aerospace engi-

neering, e.g. active vibration suppression, robotics,

large ﬂexible structures, ﬂuid instabilities in rocket

motors, etc. Hence the results obtained in this case

can be used elsewhere.

The main compromises which arise in this applica-

tion are due to two well deﬁned problems:

1. Right half plane zeros in the nominal model which

limits the achievable performance see (Freuden-

berg and Looze, 1985) and an excellent survey in

(Ser

on, 2005).

2. High relative modeling errors (multiplicative un-

certainty) in frequencies where the experimental

data is very small. This limits robust stability and

as as a consequence, the achievable robust perfor-

mance at these frequencies.

251

S. Sánchez Peña R., A. Cugueró M., Masip A., Quevedo J. and Puig V. (2005).

ACOUSTIC NOISE SUPPRESSION: COMPROMISES IN IDENTIFICATION AND CONTROL.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 251-257

DOI: 10.5220/0001172802510257

 SciTePress

Figure 1: Acoustic tube connected to the anechoic room.

2 ACOUSTIC NOISE

SUPPRESSION APPLICATION

The application is illustrated in ﬁgure 1. It consists

of a 4 meter long square tube connected, in one side

to an anechoic room and by the other to a noise gen-

erator through a primary speaker. It also contains a

reference microphone near the noise generator and

an error microphone near the control actuator (sec-

ondary speaker). The microphones are omnidirec-

tional BEHRINGER ECM8000 with linear frequency

response between 15 Hz and 20 kHz with -60 dB sen-

sitivity. The speakers are BEYMA model 5 MP60/N

of 5”, 50 W and frequency response between 50 Hz

and 12 kHz.

The primary acoustic circuit goes from the refer-

ence to the error microphone. The secondary acoustic

circuit is the one related to the feedback control sec-

tion, that goes from the control speaker to the er-

ror microphone. Primary and secondary circuits are

identiﬁed so that feedforward and/or feedback control

can be applied, respectively. The controller is imple-

mented with a DSpace DSP based on a Texas Instru-

ments TMS320C0 over a DS1003.05 (Floating-Point

Processor board).

The control scheme applies the classical method

of generating a signal as close as possible to the real

noise but with opposite phase. This can be performed

in 2 ways, by feedforward and/or by feedback. In this

work we will concentrate in this last approach, be-

cause the most interesting compromises arise in this

case. Nevertheless a great deal of noise can be elim-

inated by combining both approaches, which will be

explored in future works. Previous results in this ap-

plication area can be found in (Fang et al., 2004) and

its references. The authors have some previous expe-

rience in this area that has been presented in (Morcego

and Cuguer

o, 2001; Masip et al., 2005). The concep-

tual setup is illustrated in ﬁgure 2 and its block dia-

gram in ﬁgure 3.

Figure 2: Conceptual view of acoustic noise suppression.

3 PARAMETRIC/DYNAMIC

IDENTIFICATION

The identiﬁcation procedure is based on (Parrilo et al.,

1999; Baldelli et al., 2001), which combines para-

metric and dynamic models base on time and/or

frequency experimental input data, and solved via

LMI’s (Linear Matrix Inequalities) using the Tool-

box in (Mazzaro et al., 2004). This in turn is based

on a general rational interpolation theory developed

in (Ball et al., 1990), which combines the classical

frequency response (Nevanlinna-Pick) and time re-

sponse (Carath

eodory-Fej

er) interpolation results.

Due to the fact that the model order in classical

interpolatory results duplicates the number of data

points (in the case of frequency data), it drastically

reduces the model order to ﬁt with parametric mod-

els (usually order 2) the most signiﬁcant frequency

peaks in the time and/or frequency response. There-

fore, the remaining part of the plant can be suitably in-

terpolated by a non–parametric dynamic model. This

is valid not only in this application but in any other

−

sec

- d

Secondary

Figure 3: Feedback (FB) design setup, with primary circuit

perturbation (W

) and secondary model with multiplicative

uncertainty.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

252

Figure 4: Kautz bases ﬁtted to the secondary circuit data.

problem where well deﬁned peaks are present in the

experimental data, e.g. ﬂexible structures.

The class of a priori plant and measurement noise

models considered are in the framework presented in

(Parrilo et al., 1998) and correspond to exponentially

stable systems (ﬁnite or inﬁnite dimensional) that sat-

isfy the time domain bound

|h(k)| ≤ Kρ

−k

with K < ∞ and ρ > 1. The experimental data are

) samples of the frequency (time) response of

the system at frequency (time) values ω

). The

parametric information is ﬁtted by means of a ﬁnite

set of Kautz orthonormal basis B

(z) tuned to the ex-

perimental information as shown in (Baldelli et al.,

2001). The resulting identiﬁed model has the form:

(z) = H

(z) +

(z), p

∈ [a

, b

]

The optimization procedure which ﬁts simultane-

ously the dynamic portion H

(z) and the parame-

ters {p

, i = 1, . . . , N} is solved via a set of LMI’s,

hence it is convex. Figure 4 illustrates the ﬁtting of the

Kautz bases to the experimental information. Note

that only the ﬁrst 3 peaks have been approximated

by means of 2nd. order Kautz models, but not other

peaks that raise at frequencies above 350 Hz. The rea-

son will be explained in section 5 and has to do with

the frequencies bands where performance is critical.

In ﬁgures 5 and 12, the parametric and dynamic com-

ponents and model error of primary and secondary

acoustic circuits are presented, and in ﬁgures 6 and

7 the identiﬁed models.

From ﬁgures 5 and 12 it seems that the model error

could be sufﬁciently small to provide a representative

nominal model to design a controller. Nevertheless,

the signiﬁcance of this error varies according to the

use we will make of it, as follows:

Figure 5: Parametric and dynamic models and model iden-

tiﬁcation error of the primary circuit.

Figure 6: Identiﬁed model of the primary circuit.

Figure 7: Identiﬁed model of the secondary circuit.

ACOUSTIC NOISE SUPPRESSION: COMPROMISES IN IDENTIFICATION AND CONTROL

253

Figure 8: Uncertainty weight and multiplicative identiﬁca-

tion error.

Primary : The primary model can be used in 2 dif-

ferent ways.

• As a perturbation weight at the output for the

controller feedback (FB) design. In this case

only an approximation is enough, due to the fact

that the objective of this weight is to emphasize

the frequency bands where performance is re-

quired. In any case, the efﬁciency of the weight

in recovering the important frequency bands will

be veriﬁed at the robust performance analysis

stage.

• As a model to be used in a feedforward (FF) or

feedback/feedforward (FB/FF) scheme. Here the

model is feeded with a signal that resembles the

noise input to the actual primary circuit (as mea-

sured by the primary microfone) so that subtract-

ing both output signals at the control speaker, the

resulting acoustic noise will decrease. The efﬁ-

ciency of this procedure depends on the additive

error of this model. Hence, the error depicted in

ﬁgure 5 is the one to be considered, i.e. subtrac-

tion between model and experimental data.

Secondary : This model is used in the FB loop, and

if the plant is represented by a multiplicative uncer-

tainty set of models, the relative or multiplicative

error is important, due to the fact that both, robust

stability and performance depend on the value this

error takes. Therefore, the error illustrated in ﬁg-

ure 7 should be divided by the value of the experi-

mental data (represented in ﬁgure 7), frequency by

frequency. This can take very high values where

the experimental data is near zero magnitude, as in

ω ≈ 100 Hz in the same ﬁgure, for example

. The

multiplicative error is represented in ﬁgure 8.

It does not help to consider additive uncertainty, be-

cause the inverse of the nominal model still appears in

the robust stability test, i.e. kW

add

(z)G

−1

sec

(z)T (z)k

∞

(z)T (z)k

∞

< 1.

Figure 9: Sensitivity function and performance weight.

Figure 10: Open vs. closed loop comparison (ﬁrst design).

4 ROBUST CONTROL

The control design procedure is the standard H

∞

optimal control technique applied to solve a mixed

sensitivity problem. The objective is to mini-

mize the effect in the output of the perturbation

(acoustic noise) coming from the primary circuit

(represented by W

(z)) for all models described

by the global dynamic (multiplicative) set G

△

{[1 + W

(z)δ] G

sec

(z)}. This can be seen from ﬁg-

ure 3 and is a standard problem (Doyle et al., 1992)

that can be solved suboptimally as follows:

min

K(z)





T (z)W

(z)

S(z)W

(z)





∞

In general, the optimal solution can be provided by µ–

synthesis at the expense of a higher order controller.

Nevertheless, in this case both solutions are coinci-

dent (S

anchez Pe

na and Sznaier, 1998; Zhou et al.,

1996), due to the fact that the system is SISO.

It is clear from the above that the performance ob-

jective is to decrease the sensitivity to the signal pro-

vided by the primary circuit. In particular it is im-

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

254

Figure 11: Less interpolation points concentrated in perfor-

mance region, for secondary circuit to reduce order model.

portant to achieve this at the peaks of the primary cir-

cuit’s response. Therefore, W

(z) has been selected

such that it increases the performance in frequencies

where the primary acoustic circuit has a larger gain.

As a consequence, the sensitivity attenuation will be

greater at those peaks (see ﬁgure 9). On the other

hand, W

(z) has been obtained from the multiplica-

tive error as pointed out previously (see ﬁgure 8).

Special care has been taken to reduce this error at fre-

quencies where high performance is needed, as will

be explained in the next section.

5 IDENTIFICATION AND

DESIGN COMPROMISES

Besides maximizing performance and robustness, it

is important to consider several practical constraints

which should be taken into account. These, will there-

fore generate necessary compromises in the controller

design and in possible identiﬁcation iterations.

1. The nominal model of the (secondary) system is

stable, but has right half plane zeros.

2. The multiplicative identiﬁcation error is very difﬁ-

cult to decrease in frequency bands where the (sec-

ondary) system has a very small gain, e.g. ω ≈ 100

Hz.

3. The controller order should be kept as low as possi-

ble, due to the fact that it will be implemented with

a DSP that has limited resources.

The solutions adopted for each of these issues are ex-

posed next.

1. Non minimal phase models restrict performance

in a well known way. In fact they suffer from

the waterbed effect pointed out in (Freudenberg

and Looze, 1985; Ser

on, 2005), which determines

Figure 12: Parametric, dynamic and model error for sec-

ondary circuit (2nd design).

lower bounds in the size of the peaks of the sensi-

tivity function kS(z)k

∞

. It is clear from here that

the lower the sensitivity will be in certain bands,

the higher it will increase in others. Hence, the per-

formance weight W

should reﬂect a decrease in

the sensitivity only on those frequency bands with

the higher peaks of the primary circuit, i.e. ∆ω

in [100, 150] and [275, 350] Hz. These frequency

bands will be called “performance” bands. In this

way, nominal performance should be achieved as

follows: kW

∞

< 1.

2. The multiplicative identiﬁcation error restricts not

only robust stability, but also performance robust-

ness. Therefore it should be decreased only in the

regions where higher performance is needed, i.e.

at the “performance” bands pointed out previously.

This has been solved by adding more interpolation

points in these frequency bands, while keeping the

total number of points as low as possible not to in-

crease the order, as will be seen next.

3. The controller order is equal to the order of the

nominal model plus that of the weights W

and W

Therefore, the order of both weights have been kept

as low as possible, while taking into account the

performance and robustness features pointed out

before:

(s) =

i=1

+ sω

+ ω

(1)

(s) = 6

(s/200 + 1)

(s/10 + 1)(s/1500 + 1)

(2)

with (k

, ω

, ξ

) = (4, 125, 0.03) and

, ω

, ξ

) = (2.6, 300, 0.03). These con-

tinuous time weights have been transformed to

discrete time by means of the classical bilinear

transform with parameter 2/T

where T

is the

sampling time. On the other hand, the order of the

ACOUSTIC NOISE SUPPRESSION: COMPROMISES IN IDENTIFICATION AND CONTROL

255

nominal model has been decreased by eliminating

interpolation points and concentrating them in

the important “performance” bands. In addition,

higher frequency peaks that appear above 350 Hz

in ﬁgure 4, have not been ﬁtted with Kautz bases

for the same reason. Furthermore, a balanced

model order reduction step has been applied to the

complete model. Here, the Hankel singular values

of the discarded modes have a magnitude similar

to measurement noise, so that the identiﬁcation

error is not increased.

Figure 13: Uncertainty weight and multiplicative identiﬁca-

tion error (2nd design).

This requires a new identiﬁcation iteration for the

total design. Previously, 21 interpolating points and

a 45th. order nominal model had been obtained (see

ﬁgure 7). This in turn produced a 51st order controller

which achieved a reduction in noise, at the two impor-

tant frequency peaks of the primary circuit: 12.9dB

for the ﬁrst peak at ω = 125 Hz and 6.8dB for the

second peak at ω = 310 Hz, as illustrated in ﬁgure 10.

Next, only 12 interpolation points are considered

(ﬁgures 11 and 12) and a 25th order model is pro-

duced, which leads to a 31th. order robust controller.

Note that in ﬁgure 12, the error is lower than in the

previous case at the frequency bands [100, 150] and

[275, 350] Hz. As a consequence, the multiplicative

error is better in these “performance” regions, as il-

lustrated in ﬁgure 13.

The controller produces a slightly worst noise re-

duction performance, but still near to the previous de-

sign, 12.5dB for the ﬁrst peak and 6.17dB for the sec-

ond one, as illustrated in ﬁgure 14. This reduction

is at the expense of an ampliﬁcation at other frequen-

cies due to the waterbed effect, although at these other

frequency bands the primary gain is negligible, as we

have deliberately designed for. Compared with other

works in this area (Fang et al., 2004), this is a reason-

able result.

Figure 14: Open vs. closed loop comparison (second de-

sign).

Figure 15: Structured singular value robust performance

analysis.

The design analysis is presented in ﬁgures 15 and

16. In the ﬁrst one, nominal performance, robust sta-

bility and the robust performance test

|T (z)W

(z)| + |S(z)W

(z)| < 1, (3)

∀z = e

ΩT

are compared with the optimal measure provided by

the structured singular value µ. As indicated previ-

ously, due to the fact that the system is SISO, the lat-

ter coincides with the analysis measure provided by

(3).

Nevertheless, as observed in ﬁgure 13, the weight

does not cover completely the multiplicative error be-

low 100Hz, nor the structured singular value µ is be-

low one in ﬁgure 15. The uncertainty weight W

is used for the design stage, but the practical robust

performance measure should be provided by the ac-

tual multiplicative error in ﬁgure 13 replaced in equa-

tion (3). This can be seen in ﬁgure 16, where al-

though µ is above unity, the practical robust perfor-

mance measure remains below 1, the reason being

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

256

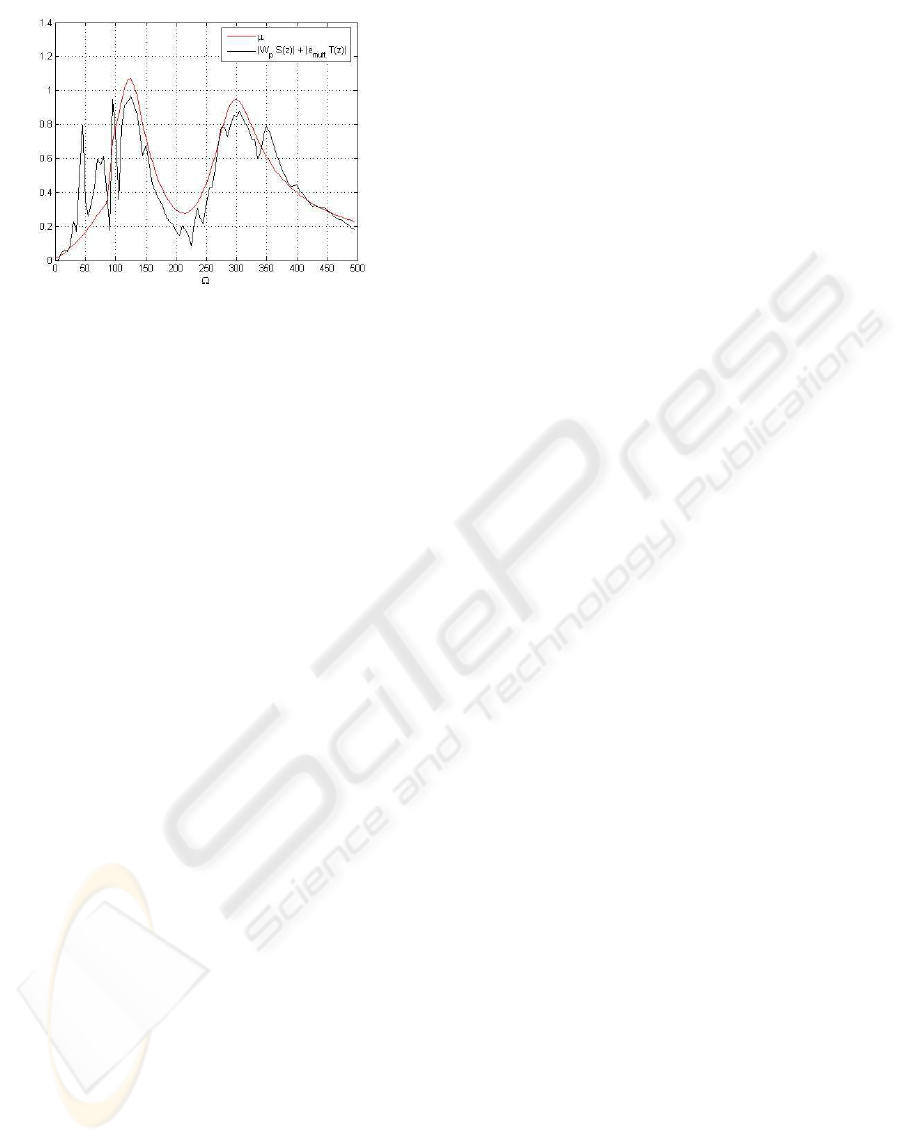
Figure 16: Practical robust performance analysis.

that in the frequency band where uncertainty is very

high, a very low performance is required.

6 CONCLUSION

Here we have presented an example of a

parametric/non–parametric identiﬁcation and ro-

bust control technique applied to acoustic noise

suppression in a tube. The main compromises,

driven by practical issues, that limit the achievable

performance have been discussed. The limitations

imposed by non minimum phase zeros, controller

model order and achievable identiﬁcation relative

error have been pointed out, and explicitly related

to performance, robustness and frequency weighted

interpolation.

The problem has been approached by general inter-

polation theory, H

∞

optimal control and µ–analysis,

as identiﬁcation, design and evaluation tools, respec-

tively. These impose well known quantitative limita-

tions on the achievable performance due to the min-

imum multiplicative uncertainty that can be practi-

cally reached by the identiﬁcation procedure, at the

expense of increasing the model order. Future work in

this area should explore parametric worst case identi-

ﬁcation and robust design methods that could bypass

this limitation to achieve a better performance and/or

obtain a lower order controller. In addition, general

feed-forward/feedback control structures will be ex-

plored as well as adaptive and/or time varying proce-

dures.

ACKNOWLEDGMENTS

The authors wish to thank the support received by the

Research Commission of the Generalitat of Catalunya

(ref. 2001SGR00236) and by Spanish CICYT (ref.

DPI2002-02147).

REFERENCES

Baldelli, D., Mazzaro, M. C., and S

anchez Pe

na, R. S.

(2001). Robust identiﬁcation of lightly damped ﬂex-

ible structures by means of orthonormal bases. IEEE

Transactions on Control Systems Technology, 9(5).

Ball, J., Gohberg, I., and Rodman, L. (1990). Interpola-

tion of Rational Matrix Functions,Operator Theory:

Advances and Applications, volume 45. Birkh

auser.

Braatz., R. D., Young, P. M., Doyle, J. C., and Morari, M.

(1994). Computational complexity of µ calculation.

IEEE Transactions on Automatic Control, 39(5).

Chen, J. and Gu, G. (2000). Control-Oriented System Iden-

tiﬁcation - An H

∞

Approach. Willey Inter-Science.

Doyle, J. C., Francis, B., and Tannembaum, A. (1992).

Feedback Control Theory. Maxwell/Macmillan.

Fang, B., Kelkar, A., Joshi, S., and Pota, H. (2004). Mod-

elling, system identiﬁcation, and contrl of acoustic-

structure dynamcs in 3D enclosures. Control Engi-

neering Practice, 12:989–1004.

Freudenberg, J. and Looze, D. (1985). Right half plane

poles and zeros and design tradeoffs in feedback

systems. IEEE Transactions on Automatic Control,

30(6):555–565.

Masip, A., Puig, V., and Quevedo, J. (2005). An optimiza-

tion based approach to interval model identiﬁcation in

the frequency domain. In Proceedings IFAC, Prague.

Mazzaro, M. C., Parrilo, P. A., and S

anchez Pe

na, R. S.

(2004). Robust identiﬁcation toolbox. Latin American

Applied Research, 34(2):91–100.

Morcego, B. and Cuguer

o, M. (2001). Comparaci

on de im-

plementaciones en C y Matlab de ﬁltros adaptativos

para DSP. In XXII Jornadas de Autom

atica (UAB),

Barcelona, Spain.

Parrilo, P. A., S

anchez Pe

na, R. S., and Sznaier, M. (1999).

A parametric extension of mixed time/frequency ro-

bust identiﬁcation. IEEE Transactions on Automatic

Control, 44(2):364–369.

Parrilo, P. A., Sznaier, M., S

anchez Pe

na, R. S., and Inanc,

T. (1998). Mixed time/frequency-domain based robust

identiﬁcation. Automatica, 34(11):1375–1389.

Puig, V., Saludes, J., and Quevedo, J. (2003). Worst-

Case simulation of discrete linear Time-Invariant in-

terval dynamic systems. Reliable Computing Journal,

9:251–290.

anchez Pe

na, R. S. and Sznaier, M. (1998). Robust Systems

Theory and Applications. John Wiley & Sons, Inc.

Ser

on, M. M. (2005). L

ımites de desempe

no y compro-

misos en sistemas de control. Revista Iberoamericana

de Autom

atica e Inform

atica Industrial, 2(1):4–18.

Zhou, K., Doyle, J. C., and Glover, K. (1996). Feedback

Control Theory. Prentice–Hall.

ACOUSTIC NOISE SUPPRESSION: COMPROMISES IN IDENTIFICATION AND CONTROL

257