
CONTRIBUTORS TO A SIGNAL FROM AN ARTIFICIAL
CONTRAST
Jing Hu and George Runger
Arizona State University
Tempe, AZ
Eugene Tuv
Intel Corporation
Chandler, AZ
Keywords:
Patterns, statistical process control, supervised learning, multivariate analysis.
Abstract:
Data from a process or system is often monitored in order to detect unusual events and this task is required in
many disciplines. A decision rule can be learned to detect anomalies from the normal operating environment
when neither the normal operations nor the anomalies to be detected are pre-specified. This is accomplished
through artificial data that transforms the problem to one of supervised learning. However, when a large
collection of variables are monitored, not all react to the anomaly detected by the decision rule. It is important
to interrogate a signal to determine the variables that are most relevant to or most contribute to the signal
in order to improve and facilitate the actions to signal. Metrics are presented that can be used determine
contributors to a signal developed through an artificial contrast that are conceptually simple. The metrics are
shown to be related to traditional tools for normally distributed data and their efficacy is shown on simulated
and actual data.
1 INTRODUCTION
Statistical process control (SPC) is used to detect
changes from standard operating conditions. In multi-
variate SPC a p×1 observation vector x is obtained at
each sample time. Some statistics, such as Hotelling’s
statistic (Hotelling, 1947), have been developed to
detect whether the observation falls in or out of the
control region representing standard operating condi-
tions. This leads to two important comments. First,
the control region is defined through an analytical ex-
pression which is based on the assumption of normal
distribution of the data. Second, after a signal further
analysis is needed to determine the variables that con-
tribute to the signal.
Our research is an extension of the classical meth-
ods in terms of the above two points. The results in
(Hwang et al., 2004) described the design of a control
region based only on training data without a distrib-
utional assumption. An artificial contrast was devel-
oped to allow the control region to be learned through
supervised learning techniques. This also allowed for
control of the decision errors through appropriate pa-
rameter values. The second question is to identify
variables that are most relevant to or most contribute
to a particular signal. We refer to these variables as
contributors to the signal. These are the variables that
receive priority for corrective action. Many industries
use an out-of-control action plan (OCAP) to react to
a signal from a control chart. This research enhances
and extends OCAP to incorporate learned control re-
gions and large numbers of variables.
A physical event, such as a broken pump or a
clogged pipe, might generate a signal from a con-
trol policy. However, not all variables might react
to this physical event. Instead, when a large collec-
tion of variables are monitored, often only a few con-
tribute tothe signal from the control policy. For exam-
ple, although a large collection of variables might be
monitored, potentially only the pressure drop across a
pump might be sensitive to a clogged pipe. The ob-
jective of this work is to identify these contributors in
order to improve and facilitate corrective actions.
It has been a challenge for even normal-theory
based methods to completely solve this problem. The
key issue is the interrelationships between the vari-
ables. It is not sufficient to simply explore the mar-
ginal distribution of each variable. This is made clear
3
Hu J., Runger G. and Tuv E. (2005).
CONTRIBUTORS TO A SIGNAL FROM AN ARTIFICIAL CONTRAST.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 3-10
DOI: 10.5220/0001172900030010
Copyright
c
SciTePress

in our illustrations that follow. Consequently, early
work (Alt, 1985; Doganaksay et al., 1991) required
improvement. Subsequent work under normal theory
considered joint distributions of all subsets of vari-
ables (Mason et al., 1995; Chua and Montgomery,
1992; Murphy, 1987). However, this results in a
combinatorial explosion of possible subsets for even
a moderate number of variables. In (Rencher, 1993)
and (Runger et al., 1996) an approach based on con-
ditional distributions was used that resulted in feasi-
ble computations, again for normally distributed data.
Only one metric was calculated for each variable.
Furthermore, in (Runger et al., 1996) a number of rea-
sonable geometric approaches were defined and these
were shown to result in equivalent metrics. Still, one
metric was computed for each variable. This idea is
summarized briefly in a following section. Although
there are cases where the feasible approaches used in
(Rencher, 1993) and (Runger et al., 1996) are not suf-
ficient, they are effective in many instances, and the
results indicate when further analysis is needed. This
is illustrated in a following section.
The method proposed here is a simple, computa-
tionally feasible approach that can be shown to gen-
eralize the normal-theory methods in (Rencher, 1993)
and (Runger et al., 1996). Consequently, it has the ad-
vantage of equivalence of a traditional solution under
traditional assumptions, yet provides a computation-
ally and conceptually simple extension. In Section 2
a summary is provided of the use of an artificial con-
trast with supervised learning is to generate a control
region. In Section 3 the metric used for contributions
is presented. The following section present illustra-
tive examples.
2 CONTROL REGION DESIGN
Modern data collection techniques facilitate the col-
lection of in-control data. In practice, the joint distri-
bution of the variables for the in-control data is un-
known and rarely as well-behaved as a multivariate
normal distribution. If specific deviations from stan-
dard operating conditions are not a priori specified,
leaning the control region is a type of unsupervised
learning problem. An elegant technique can be used
to transform the unsupervised learning problem to a
supervised one by using an artificial reference distrib-
ution proposed by (Hwang et al., 2004). This is sum-
marized briefly as follows.
Suppose f(x) is an unknown probability density
function of in-control data, and f
0
(x) is a specified
reference density function. Combine the original data
set x
1
, x
2
, ..., x
N
sampled from f
0
(x) and a random
sample of equal size N drawn from f
0
(x).If we as-
sign y = −1 to each sample point drawn from f(x)
and y = 1 for those drawn from f
0
(x), then learning
control region can be considered to define a solution
to a two-class classification problem. Points whose
predicted y are −1 are assigned to the control region,
and classified into the “standard” or “on-target” class.
Points with predicted y equal to 1 are are classified
into the“off-target” class.
For a given point x, the expected value of y is
µ(x) = E(y|x) = p(y = 1|x) − p(y = −1|x)
= 2p(y = 1|x) − 1
Then, according to Bayes’ Theorem,
p(y = −1|x) =
p(y = −1|x)
p(x)
=
p(x| − 1)p(y = −1)
p(x| − 1)p(y = −1) + p(x|1)p(y = 1)
=
f(x)
f(x) + f
0
(x)
(1)
where we assume p(y = 1) = p(y = −1) for train-
ing data, which means in estimating E(y|x) we use
the same sample size for each class. Therefore, an
estimate of the unknown density f(x) is obtained as
ˆ
f(x) =
1 − bµ(x)
1 + bµ(x)
× f
0
(x), (2)
where f
0
(x) is the known reference probability den-
sity function of the random data and ˆµ(x)is learned
from the supervised algorithm. Also, the odds are
p(y = −1|x)
p(y = 1|x)
=
f(x)
f
0
(x)
(3)
The assignment is determined by the value of ˆµ(x).
A data x is assigned to the class with density f (x)
when
bµ(x) < v,
and the class with density f
0
(x) when
bµ(x) > v.
where v is a parameter that can used to adjust the error
rates of the procedure.
Any supervised learner is a potential candidate to
build the model. In our research, a Regularized Least
Square Classifier (RLSC) (Cucker and Smale, 2001)
is employed as the specific classifier. Squared error
loss is used with a quadratic penalty term on the co-
efficients (from the standardization the intercept is
zero). Radial basis functions are used at each ob-
served point with common standard deviation. That
is the mean of y is estimated from
µ(x) = β
0
+
n
X
j=1
β
j
exp
−
1
2
kx − x
j
k
2
/σ
2
= β
0
+
n
X
j=1
β
j
K
σ
(x, x
j
) (4)
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
4

Also, let β = (β
1
, . . . , β
n
). The β
j
are estimated
from the penalized least squares criterion
min
β
0
,β
n
i=1
y
i
− β
0
−
n
j=1
β
j
exp
−
1
2
kx − x
j
k
2
/σ
2
2
+ γkβk
2
(5)
where n is the total number of observations in the
training data set. If the x’s and y are standardized
to mean zero then it can be shown that
b
β
0
= 0. Also,
let the matrix K denote the n ×n matrix with (i, j)th
element equal to K
σ
(x
i
, x
j
). Then for a fixed σ the
solution for β is
b
β = (K + nγI)
−1
y (6)
and this is used to estimate µ(x).
3 CONTRIBUTORS TO A SIGNAL
In this section, a metric is developed to identify vari-
ables that contribute to a signal from SPC based upon
artificial contrasts. Suppose there are p correlated
variables (x
1
, x
2
, . . . , x
p
). Let x
∗
be an observed data
point that results in a signal from the control scheme.
Define the set
L
k
= {x|x
i
= x
∗
i
, i 6= k}
There are several reasonable metrics for the contri-
bution of variable x
k
to the out-of-control signal. We
use
η
k
(x
∗
) = max
x∈L
k
b
f(x)
b
f(x
∗
)
(7)
This measures the change from
b
f(x)/
b
f(x
∗
) that can
be obtained from only a change to x
k
. If η
k
(x
∗
) is
small then x
∗
k
is not unusual. If η
k
(x
∗
) is large, then a
substantial change can result from a change to x
k
and
x
k
is considered to be an important contributor to the
signal.
From (2) it can be shown that bµ(x) is a monotone
function of the estimated density ratio
b
f(x)/
b
f
0
(x).
Therefore, the value x
k
∈ L
k
that maximizes the es-
timated density ratio also maximizes bµ(x) over this
same set. In the special case that f
0
(x) is a uniform
density the value of x
k
∈ L
k
that maximizes bµ(x)
also maximizes
b
f(x) over this set. Consequently,
η
k
(x
∗
) considers the change in estimated density that
can be obtained from a change to x
k
.
From (3) we have that η
k
is the maximum odds ra-
tio obtained over L
k
η
k
(x
∗
) = max
x∈L
k
ˆp(y = −1|x)/ˆp(y = 1|x)
ˆp(y = −1|x
∗
)/ˆp (y = 1|x
∗
)
(8)
To compare values of η
k
(x
∗
) over k the denominator
in (8) can be ignored and the numerator is a monotone
function of ˆp(y = −1|x). Consequently, the value in
L
k
that maximizes η
k
(x
∗
) is the one that maximizes
ˆp(y = −1|x). Therefore, the η
k
(x
∗
) metric is similar
to one that scores the change in estimated probability
of an in-control point.
A point that is unusual simultaneously in more than
one variable, but not in either variable individually, is
not well identified by this metric. That is, if x
∗
is
unusual in the joint distribution of (x
1
, . . . , x
k
) for
k ≤ p, but not in the conditional marginal distribu-
tion of f(x
i
|x
j
= x
∗
j
, i 6= j) then the metric is not
sensitive. This implies that the point is unusual in a
marginal distribution of more than one variable. Con-
sequently, one can consider a two-dimensional set
L
jk
= {x|x
i
= x
∗
i
, i 6= j, k}
and a new metric
η
jk
(x
∗
) = max
x∈L
jk
b
f(x)
b
f(x
∗
)
(9)
to investigate such points. This two-dimensional met-
ric would be applied if none of the one-dimensional
metrics η
k
(x
∗
) are unusual. Similarly, higher-
dimensional metrics can be defined and applied as
needed. The two-dimensional metric η
jk
(x
∗
) would
maximize the the estimated density over x
j
and x
k
. It
might use a gradient-based method or others heuris-
tics to conduct the search. The objective is only to
determine the pair of variables that generate large
changes in the estimated density. The exact value
of the maximum density is not needed. This per-
mits large step sizes to be used in the search space.
However, the focus of the work here is to use the
one-dimensional metrics η
k
(x
∗
)’s. Because the con-
tribution analysis is only applied to a point which
generates a signal, no information for the set of one-
dimensional η
k
’s implies that a two-dimensional (or
higher) metric needs to be explored. However, the
one-dimensional η
k
’s are effective in many cases, and
they provide a starting point for all cases.
3.1 Comparison with a Multivariate
Normal Distribution
In this section, we assume the variables follow a mul-
tidimensional normal distribution. Under these as-
sumptions, we can determine the theoretical form of
the metric η
k
(x
∗
). Given the estimate of the unknown
density
b
f(x), define x
0
as
x
0
= argmax
x∈L
k
b
f(x)
For a multivariate normal density with mean vector µ
and covariance matrix Σ
x
0
= argmin
x∈L
k
(x − µ)
′
Σ
−1
(x − µ)
Therefore, x
0
is the point in L
k
at which Hotelling’s
statistic is minimized. Consequently, x
0
is the same
CONTRIBUTORS TO A SIGNAL FROM AN ARTIFICIAL CONTRAST
5

point used in (Runger et al., 1996) to define the contri-
bution of variable x
k
in the multivariate normal case.
The use of the metric in (7) generalizes this previous
result from a normal distribution to an arbitrary distri-
bution.
4 ILLUSTRATIVE EXAMPLE
4.1 Learning the In-Control
Boundary
To demonstrate that our method is an extension of the
traditional method, first we assume that the in-control
data follow a multivariate normal distribution. In the
case of two variables, we capture a smooth, closed
elliptical boundary. Figure (1) shows the boundary
learned through an artificial contrast and a supervised
learning method along with the boundary specified
by Hotelling’s statistic (Hotelling, 1947) for the in-
control data.
The size of in-control training data is 400 and the
size of uniform data is also 400. The in-control train-
ing data are generated from the two-dimensional nor-
mal distribution X = C ∗ Z with covariance
Cov(X) = CC
′
=
1 0.5
0.5 1
and Z following two-dimensional joint standardized
normal distribution with ρ = 0. The smoothing para-
meter for the classifier is γ = 4/800. The parameter
for the kernel function is σ =
√
8. The out-of-control
training data are generated from the reference distri-
bution. There are four unusual points: A (3, 0), B
(3, 1), C (3, 2), and D (3, 3).
−4 −3 −2 −1 0 1 2 3 4
−4
−3
−2
−1
0
1
2
3
4
x
1
x
2
Boundaries
A
B
C
D
Tsquare: α=0.005
Constrast: cutoff=0
Constrast: cutoff=0.2
Constrast: cutoff=0.4
in−control data
out−of−control data
Figure 1: Learned Boundaries and Hotelling’s Boundary
Table 1: Type I error for In-control Data
cut-off value 0 0.2 0.4
the training data 0.085 0.0325 0.015
the testing data 0.1 0.0525 0.025
Table 2: Type II error for Out-of-control Data with Different
Shifted Means
cut-off value 0 0.2 0.4
(1,0) 0.785 0.895 0.96
(1,1) 0.7275 0.8325 0.8975
(2,0) 0.4875 0.6125 0.7325
(2,2) 0.3225 0.45 0.565
(3,0) 0.1025 0.215 0.325
(3,3) 0.055 0.1025 0.185
Testing data sets are used to evaluate performance,
that is, Type I error and Type II error of the classifier.
They are generated from similar multivariate normal
distributions with or without shifted means. Each test-
ing data set has a sample size of 400.
Table 1 gives the Type I error for the training data
and for the testing data whose mean is not shifted. It
shows that the Type I error decreases when the cut-
off value of the boundary increases. Table 2 gives the
Type II error for the testing data with shifted mean. It
shows that for a given shift, the Type II error increases
when the cut-off value of the boundary increases. It
also illustrates that, for a given cut-off value, the fur-
ther the mean shifts from the in-control mean, the
lower the Type II error.
4.2 Contribution Evaluation
The probability density function of the in-control data
f(x) is estimated by (2). For the normal distribution
in Section 3.1 examples are provided in the cases of
two-dimensions (Figure 2)and 30-dimensions (Figure
3).
For the case of two dimensions, Figure (1) shows 4
points at (3, 0), (3, 1), (3, 2), (3, 3). The correspond-
ing curves for
b
f(x) for each point are shown in Fig-
ure (4) through Figure (7). These figures show that
the variable that would be considered to contribute
to the signal for points (3, 0) and (3, 1) is identified
by the corresponding curve. For point (3, 2) the vari-
able is not as clear and the curves are also ambiguous.
For the point (3, 3) both variables can be considered
to the signal and this is indicated by the special case
where all curve are similar. That is, no proper subset
of variables is identified and this is an example where
a higher-dimensional analysis (such as with η
jk
(x
∗
))
is useful.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
6

−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
Based on Means
f(x
1
,mu
2
)
f(mu
1
,x
2
)
Figure 2: Density estimate for two dimensions
−4 −3 −2 −1 0 1 2 3 4
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
x 10
−26
Based on Means
Figure 3: Density estimate for thirty dimensions
4.3 Example in 30 Dimensions
For a higher dimensional example, consider p = 30
dimensions. Out-of-control points are generated and
density curves are produced for each variable. These
curves are proportional to the conditional density with
all the other variables at the observed values. For p =
30 the size of in-control training data is 200 and the
size of the uniform data is also 200. Curves for out-
of-control points
A = (3, 0, . . . , 0)
B = (3, −3, 0, . . . , 0)
C = (3, 3, . . . , 3)
are generated. For p = 30 dimensions the density
curves are shown in Figure (8) through Figure (10).
−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Based on Values
k=1
k=2
(3 0)
Figure 4: f(x
1
, 0) and f (3, x
2
)
−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Based on Values
k=1
k=2
(3 1)
Figure 5: f(x
1
, 1) and f (3, x
2
)
Note that the changes in density match the contrib-
utors to an unusual point. Note that for point C the
density metric does not indicate any subset of vari-
ables as contributors. This is a special case and such a
graph implies that all variables contribute to the signal
from the chart because these graphs are only gener-
ated after a signal from a control has been generated.
Such a special case is also distinguished from cases
where only a proper subset of variables contribute to
the signal.
For the particular case of p = 30 dimensions,
values of η
k
(x
i
) are calculated for these points and
k = 1, . . . , 30 in Figure (11) through Figure (13).
The results indicate the this metric can identify vari-
ables that contribute to the signal. For point C simi-
lar comments made for the density curves apply here.
The metric does not indicate any subset of variables as
contributors. This is a special case and such a graph
CONTRIBUTORS TO A SIGNAL FROM AN ARTIFICIAL CONTRAST
7

−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Based on Values
k=1
k=2
(3 2)
Figure 6: f(x
1
, 2) and f (3, x
2
)
−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Based on Values
k=1
k=2
(3 3)
Figure 7: f(x
1
, 3) and f (3, x
2
)
implies that all variables contribute to the signal from
the chart.
5 MANUFACTURING EXAMPLE
The data set was from a real industrial process. There
are 228 samples in total. To illustrate our problem,
we use two variables. Here, Hotelling T
2
is employed
to find out in-control data. The mean vector and co-
variance matrix are estimated from the whole data set
and T
2
follows a χ
2
distribution with two degrees of
freedom. The false alarm, α, is set as 0.05 in order
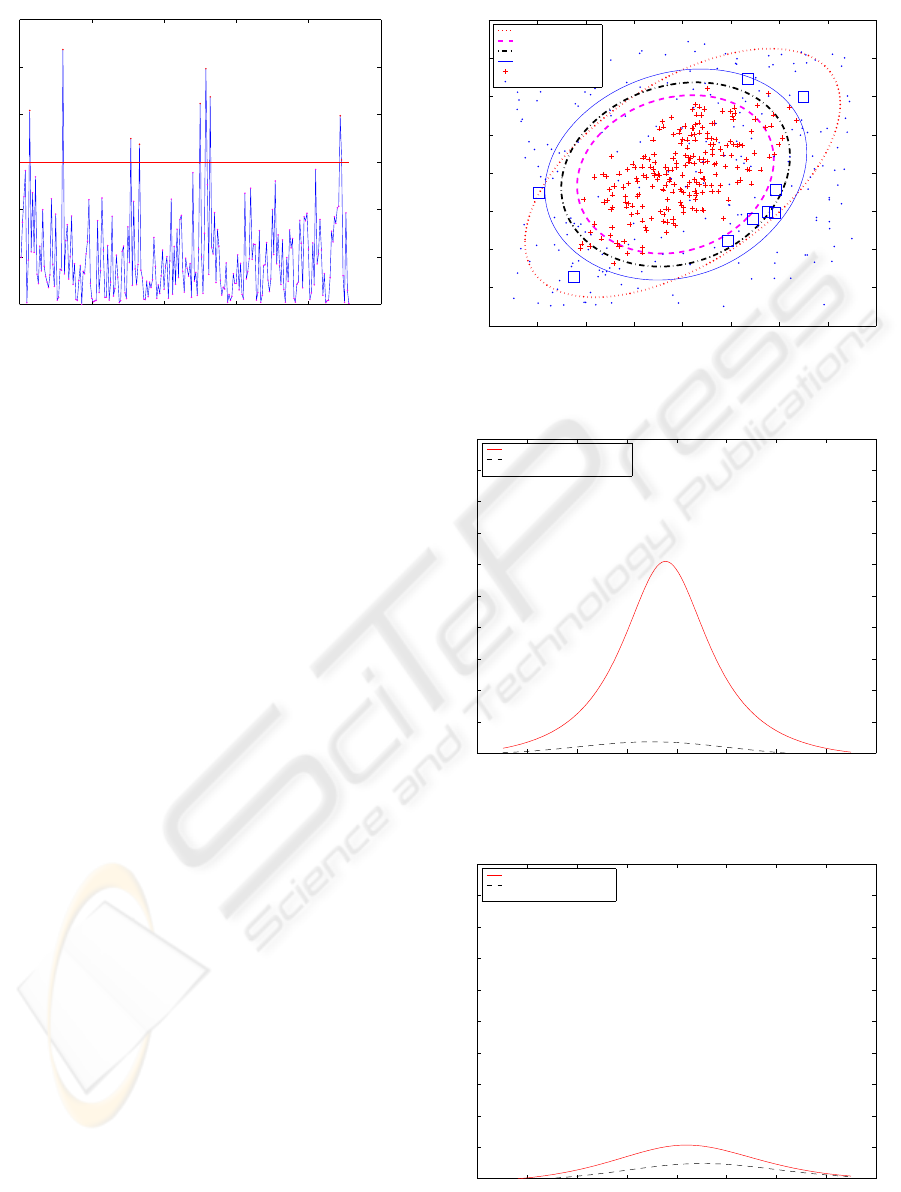
to screen out unusual data. Figure (14) displays the
Hotelling T
2
for each observation. From the results,
we obtain 219 in-control data points that are used as
the training data.
−4 −3 −2 −1 0 1 2 3 4
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
x 10
−26
Based on ValuesPoint 1
k=1
Figure 8: Density f(x) as a function of x
k
for k =
1, 2, . . . , 30 for Point A
−4 −3 −2 −1 0 1 2 3 4
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
x 10
−26
Based on ValuesPoint 2
k=1
k=2
Figure 9: Density f(x) as a function of x
k
for k =
1, 2, . . . , 30 for Point B
Figure (15) shows the learned boundaries with dif-
ferent cut-off values and the Hotelling T
2
boundary
with α being 0.005. The learned boundary well cap-
tures the characteristic of the distribution of the in-
control data. We select the learned boundary with
cut-off v = 0.4 as the decision boundary and obtain
three unusual points: Point 1, 2, and 4. The metric is
applied to Point 2 and 4 and Table (3) and it demon-
strates η values for each dimension for each point.
Figure (16) and Figure (17) demonstrate f(x
1
, x
2
)
when as functions of x
1
and x
2
for Point 2 and 4,
respectively. For Point 2, η
1
is significantly larger
than η
2
so the first variable contributes to the out-of-
control signal. For Point 4, η
1
and η
2
are close so both
variables contributes to the out-of-control signal.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
8

−4 −3 −2 −1 0 1 2 3 4
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
x 10
−26
Based on ValuesPoint 3
Figure 10: Density f (x) as a function of x
k
for k =
1, 2, . . . , 30 for Point C
0 5 10 15 20 25 30
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Dimension
η
Based on Values: Point 3
Figure 11: Contributor metric η
k
for variables k =
1, 2, . . . , 30 for Point A
6 CONCLUSION
A supervised method to learn normal operating con-
ditions provides a general solution to monitor systems
of many types in many disciplines. In addition to
the decision rule it is important to be able to inter-
rogate a signal to determine the variables that con-
tribute to it. This facilitates an actionable response
to a signal from decision rule used to monitor the
process. In this paper, contributors to a multivari-
ate SPC signal are identified from the same func-
tion that is learned to define the decision rule. The
approach is computationally and conceptually sim-
ple. It was shown that the method generalizes a tra-
ditional approach for traditional multivariate normal
theory. Examples show that the method effectively re-
0 5 10 15 20 25 30
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Dimension
η
Based on Values: Point 3
Figure 12: Contributor metric η
k
for variables k =
1, 2, . . . , 30 for Point B
0 5 10 15 20 25 30
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Dimension
η
Based on Values: Point 3
Figure 13: Contributor metric η
k
for variables k =
1, 2, . . . , 30 for Point C
produces solutions for known cases, yet it generalizes
to a broader class of problems. The one-dimensional
metric used here would always be a starting point for
such a contribution analysis. Future work is planned
to extend the metric to two- and higher-dimensions
to better diagnose contributors for cases in which the
one-dimensional solution is not adequate.
Table 3: η for Point 2 and 4
η
1
η
2
Point 2 16.791 1.0001
Point 4 3.6737 1.6549
CONTRIBUTORS TO A SIGNAL FROM AN ARTIFICIAL CONTRAST
9
0 50 100 150 200 250
0
2
4
6
8
10
12
Hotelling Tsquare Chart, UCL=5.9915
1
2
3
4
5
6
7
8
9
Figure 14: Hotelling T
2
REFERENCES
Alt, F. B. (1985). Multivariate quality control. In Kotz, S.,
Johnson, N. L., and Read, C. R., editors, Encyclope-
dia of Statistical Sciences, pages 110–122. John Wiley
and Sons, New York.
Chua, M. and Montgomery, D. C. (1992). Investigation and
characterization of a control scheme for multivariate
quality control. Quality and Reliability Engineering
International, 8:37–44.
Cucker, F. and Smale, S. (2001). On the mathematical foun-
dations of learning. Bulletin of AMS, 39:1–49.
Doganaksay, N., Faltin, F. W., and Tucker, W. T. (1991).
Identification of out-of-control quality characteris-
tics in a multivariate manufacturing environment.
Communications in Statistics-Theory and Methods,
20:2775–2790.
Hotelling, H. (1947). Multivariate quality control-
illustrated by the air testing of sample bombsights.
In Eisenhart, C., Hastay, M., and Wallis, W., edi-
tors, Techniques of Statistical Analysis, pages 111–
184. McGraw-Hill, New York.
Hwang, W., Runger, G., and Tuv, E. (2004). Multivariate
statistical process control with artificial contrasts. un-
der review.
Mason, R. L., Tracy, N. D., and Young, J. C. (1995). De-
composition of T
2
for multivariate control chart inter-
pretation. Journal of Quality Technology, 27:99–108.
Murphy, B. J. (1987). Selecting out-of-control variables
with T
2
multivariate quality control procedures. The
Statistician, 36:571–583.
Rencher (1993). The contribution of individual variables to
hotelling’s T
2
, wilks’ Λ, and R
2
. Biometrics, 49:479–
489.
Runger, G. C., Alt, F. B., and Montgomery, D. C. (1996).
Contributors to a multivariate control chart signal.
Communications in Statistics - Theory and Methods,
25:2203–2213.
−4 −3 −2 −1 0 1 2 3 4
−4
−3
−2
−1
0
1
2
3
4
x
1
x
2
Boundaries
1
2
3
4
5
6
7
8
9
Tsquare: α=0.005
Constrast: cutoff=0
Constrast: cutoff=0.2
Constrast: cutoff=0.4
in−control data
out−of−control data
Figure 15: Learned Boundaries and Hotelling T
2
−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Based on Values
k=1
k=2
Point 2 : (−2.9758 −0.51562)
Figure 16: Density f(x) as a function of x
1
and x
2
for Point
2
−4 −3 −2 −1 0 1 2 3 4
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Based on Values
k=1
k=2
Point 4 : (2.492 1.9968)
Figure 17: Density f(x) as a function of x
1
and x
2
for Point
4
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
10
