A SWITCHING ALGORITHM FOR TRACKING EXTENDED

TARGETS

Andreas Kr

außling, Frank E. Schneider and Dennis Wildermuth

FGAN – Research Institute for Communications, Information Processing and Ergonomics

Neuenahrer Straße 20, 53343 Wachtberg–Werthhoven, Germany

Keywords:

Tracking, Kalman ﬁlter, Viterbi algorithm, crossing targets.

Abstract:

Tracking extended objects like humans in crowded environments is one of the challenges in mobile robotics.

Several characteristics must be taken into consideration when evaluating the performance of such a tracking

algorithm — e.g. accuracy, the need for computation time and the ability to deal with complex situations

like crossing targets. In this paper two different algorithms for tracking extended targets are examined and

compared by means of these criterions. One result is that none of the algorithms alone is a sufﬁcient solution

to the criterias. Therefore, a switching approach using both algorithms is introduced and tested on real data.

1 INTRODUCTION AND

RELATED WORK

One aspect in mobile robotics is the assistance of hu-

mans in order to accomplish a task (e.g. support el-

derly people). A precondition for this usage is that the

robot is able to follow the human partner. Therefore,

it is necessary that the robot has the ability to estimate

the current position of the human. This problem can

be analysed under the superordinate concept of track-

ing. Tracking denotes the estimation of the position

of an object based on consecutive sensor measure-

ments. It is well studied in the ﬁeld of aerial surveil-

lance with radar devices (Bar-Shalom and Fortmann,

1988). In the area of mobile robots tracking is also a

well established research topic (Prassler et al., 1999),

(Schulz et al., 2001), (Fod et al., 2002) and (Fuer-

stenberg et al., 2002). In mobile robotics laser range

scanners are one of the preferred sensor devices. A

Sick laser range scanner for example can measure the

distance to the next reﬂecting obstacle with a high

angle resolution of e.g. 0.25 degree. Lasers have

rapidly gained popularity for mobile robotic applica-

tions such as collision avoidance, navigation, local-

ization and map building in the recent years (Thrun,

1998), (Thrun et al., 1999).

The problem of tracking people and other objects in

densely populated environments with a robot–borne

laser scanner can be characterized in the following

way: most of the readings are from obstacles like

walls or other objects and only a few measurements

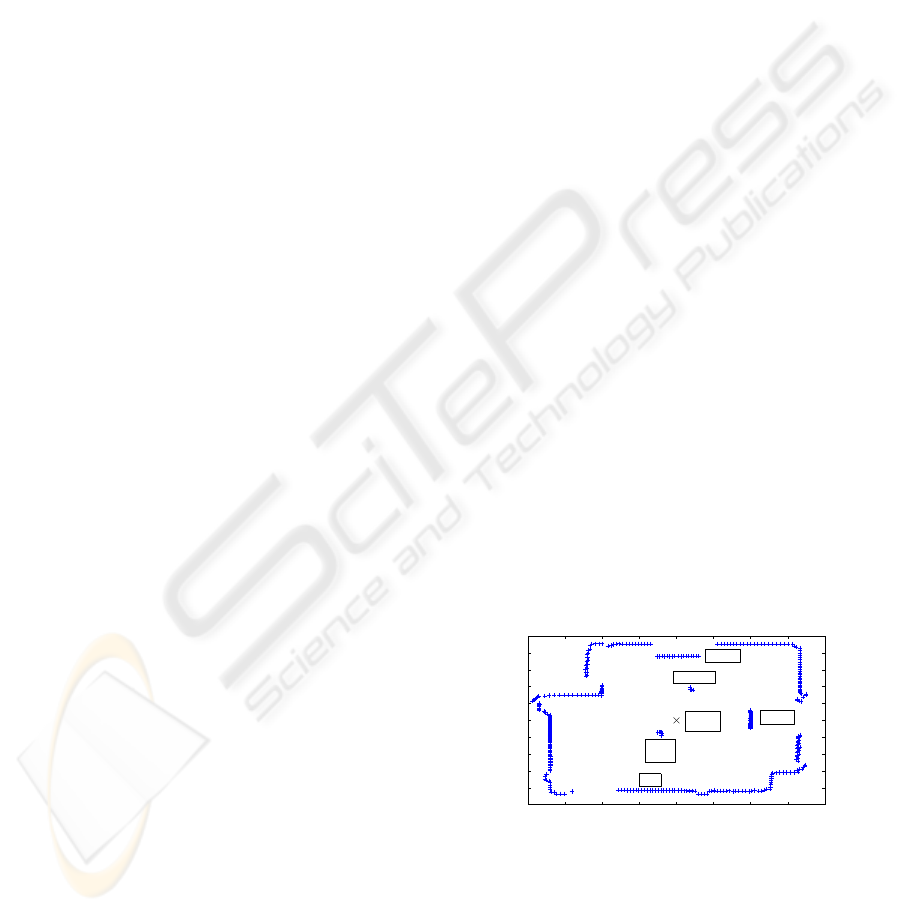
come from the tracked object itself. This fact is illus-

trated in ﬁgure 1. It shows the measurements of one

scan in a real system in our laboratory. In the scenario

the observing robot, at which two Sick lasers with a

180 degree ﬁeld of view each are mounted back to

back, is located in the centre with coordinates (0, 0).

There are two humans in the ﬁeld of view of the ro-

bot. Furthermore, there are two wall–like obstacles.

Most of the measurements originate from the walls

of the laboratory. The problem of allocation of data

−800 −600 −400 −200 0 200 400 600 800

−1000

−800

−600

−400

−200

200

400

600

800

1000

second

person

first person

observing

robot

obstacle

wall

Figure 1: Measurements of one scan.

obtained from the presently accounted target is called

the data association problem (Bar-Shalom and Fort-

mann, 1988). As a solution to this problem, a tracking

algorithm might use a validation gate which separates

the signals belonging to the current target from other

signals. A second characteristic of tracking people

126

Kräußling A., E. Schneider F. and Wildermuth D. (2005).

A SWITCHING ALGORITHM FOR TRACKING EXTENDED TARGETS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 126-133

DOI: 10.5220/0001173601260133

 SciTePress

with laser range scanners is the occurrence of several

measurements from the same object. In contrast to

common radar based tracking sensors the Sick laser

scanner has a much higher resolution and refresh rate.

This leads to the fact that the tracked object gener-

ates several measurements. Therefore, we have to

deal with what we call extended objects instead of

punctiform objects like in the common radar track-

ing literature. Thereby, punctiform targets are those

ones, which are just origin of one measurement. A

third characteristic of tracking in the ﬁeld of mobile

robotics is the occurrence of crossing targets. This

means that two targets get very close to each other,

so that they cannot be separated by common tracking

algorithms (Fortmann et al., 1983), (Kr

außling et al.,

2004b). This situation can appear e.g. when two hu-

mans meet, talk to each other and split again and is

a well known problem in mobile robotics (Prassler

et al., 1999).

In section 2 we introduce two algorithms which

can deal with tracking extended objects as long as

they are not crossing. The ﬁrst algorithm just makes

use of the Kalman ﬁlter (Kalman, 1960), whereas

the second one also is based on the Viterbi algorithm

(Viterbi, 1967). The application of the Kalman ﬁl-

ter has a long tradition in mobile robotics (Crowley,

1989), (Leonard and Durrant-Whyte, 1992) and (Dis-

sanayake et al., 2001). Additionally, the underlying

models for the dynamics and the observation process

of the object are proposed and the details of the val-

idation gate are given. In section 3 the results of the

comparison of the accuracy and the computation com-

plexity of the algorithms are summarized. The com-

parison of different algorithms is a well introduced

issue in mobile robotics (Gutmann et al., 1998) and

(Gutmann and Fox, 2002). In section 4 the perfor-

mance of the algorithms under the condition of cross-

ing targets is studied and it is shown, that none of

the algorithms can handle this situation sufﬁciently.

Therefore an improved algorithm based on the Viterbi

algorithm is introduced. In section 5 a new hybrid

or switching algorithm, which is the main contribu-

tion of this work, is proposed as a possible solution of

the tracking problem in mobile robotics. It uses the

improved algorithm only when a crossing occurs and

otherwise it just uses a simple Kalman ﬁlter. The per-

formance of the switching algorithm is tested on real

data in detail. Finally, in section 6 the summary and

an outlook on future work are given.

2 THE MATHEMATICAL

BACKGROUD OF THE

ALGORITHMS

2.1 The model

The dynamics of the object to be observed and the

observation process itself are modeled by a hidden

Gauß–Markov chain with the equations

= Ax

k−1

+ w

k−1

(1)

and

= Bx

+ v

. (2)

Thereby x

is the object state vector at time k, A is the

state transition matrix, z

is the observation vector at

time k and B is the observation matrix. Furthermore,

and v

are supposed to be uncorrelated zero mean

white Gaussian noises with covariances Q and R.

Since the motion of a target in the plane has to be

described a two dimensional kinematic model is used.

Therefore, it is

= (

˙x

)

⊤

(3)

with x

and x

the Cartesian coordinates of the tar-

get and ˙x

and ˙x

the corresponding velocities. z

gives just the Cartesian coordinates of the target. For

the coordinates the equation of a movement with con-

stant velocity is holding, i.e. it is

k+1,j

= x

+ ∆T ˙x

. (4)

Thereby ∆T is the time interval between two consec-

utive measurements. For the progression of the veloc-

ities we the equation

˙x

k+1,j

= e

−∆T/Θ

˙x

+ Σ

1 − e

−2∆T/Θ

u(k) (5)

from (van Keuk, 1971) with the zero mean white

Gaussian noise u(k) with E[u(m)u(n)

⊤

] = δ

Thus the velocity is supposed to decline exponen-

tially. The term

1 − e

−2∆T/Θ

u(k) (6)

models the process noise and the accelerations. For

the details of the resulting matrices A, B, Q and R

we refer to (Kr

außling et al., 2005).

2.2 The validation gate

The validation gate is realised using the Kalman ﬁlter.

The Kalman ﬁlter calculates a prediction y(k + 1|k)

for the measurements z

k+1,l

from the actually han-

dled target at time step k + 1 via the formula

y(k + 1|k) = B · A · x(k|k). (7)

A SWITCHING ALGORITHM FOR TRACKING EXTENDED TARGETS

127

Thereby x(k|k) is the estimate for the position of the

target at time step k. For every sensor reading z

k+1,l

of the time step k+1 (l = 1, . . . 360) the Mahalanobis

distance λ (Mahalanobis, 1936) with

λ = (z

k+1,l

− y(k + 1|k))

⊤

· [S(k + 1)]

−1

·(z

k+1,l

− y(k + 1|k)) (8)

is computed. Then all measurements with λ >

max

with a given treshold λ

max

are excluded. See

(Bar-Shalom and Fortmann, 1988) for further details.

Thereby the matrix S(k+1) is the innovations covari-

ance from the Kalman ﬁlter. In common ﬁlter appli-

cations this matrix is calculated from the predictions

covariance P (k + 1|k) with the equation

S(k + 1) = BP (k + 1|k)B

⊤

+ R (9)

with the given covariance matrix R of the measure-

ment noise. The predictions covariance is derived

from the equation

P (k + 1|k) = AP (k|k)A

⊤

+ Q. (10)

But for tracking extended objects this approach is not

sufﬁcient, since there is an additional inﬂuence of the

extendedness of the object to the deviation of the mea-

surements from the prediction y(k+1|k). To take care

of this feature an accessory positive deﬁnite matrix E

should be added in equation 9. Because the lateral di-

mension of people usually shows a radius in the range

of 30 cm, the entries of E should be in the range of

900. Thus, after some optimization process we used

E =



780 0

0 780



(11)

and

S(k + 1) = BP (k + 1|k)B

⊤

+ R + E. (12)

Thereby the values of the entries of the matrix E

vastly exceed the values of the entries of the matrix

R, so that the main contribution in equation 12 comes

from the matrix E. Of course, a more elaborated

model of the target shape like in (Guivant and Nebot,

2001), (Taylor and Kleeman, 2004) or in (Zhao and

Shibasaki, 2005) could be used. These authors have

developed models for walking, modeling the move-

ment of the two legs of a person explicitly. Thereby

they make use of the fact that the laser scanners are

usually mounted at the height of the legs. We have

rejected such an approach because of the computa-

tional burden aligned with these approaches. More-

over looking at the actual data we get from the laser

scanners we found that its hard to separate the legs

of the persons in most of the scans. Finally, as one

of the references has already mentioned, the situation

can get very complex when there are crossing targets

(Taylor and Kleeman, 2004). This can result in a dra-

matic increase of the number of hypothesis used for

the modeling of the walking persons.

One characteristic of the model proposed in this pa-

per consists of the fact, that the sequence {K

}

∞

k=1

the Kalman gains (please note equation 15 for a de-

ﬁnition) converges very rapidly to a limit. Thus the

calculations of the matrices K

can be omitted and

instead it is sufﬁcient to calculate and use the limit

K = lim

k→∞

. This limit can be calculated quite

easily, similar to the case of the α–β–ﬁlter described

in (Ekstrand, 1983) or (Kalata, 1984). These facts can

be exploited for the development of a tracking algo-

rithm for real time applications.

2.3 The Kalman ﬁlter algorithm

with equal weights

This algorithm ﬁrst calculates an unweighted mean

k+1

of the m

k+1

measurements {z

k+1,l

}

k+1

l=1

, that

have been selected by the gate, i.e. it is

k+1

l=1

k+1,l

. (13)

This mean is used as the input for the updating equa-

tion of the Kalman ﬁlter, i.e. it is

x(k+1|k+1) = x(k+1|k)+K

k+1

−y(k+1|k))

(14)

with the predictions x(k + 1|k) = Ax(k|k) and

y(k + 1|k) and the Kalman gain K

k+1

derived from

the Kalman ﬁlter via the formula

k+1

= P (k + 1|k)B

⊤

[S(k + 1)]

−1

(15)

or as supposed above by using the limit K of the se-

quence {K

}

∞

k=1

. The covariances are then updated

with the equation

P (k+1|k+1) = P (k+1|k)−K

k+1

S(k+1)[K

k+1

]

⊤

(16)

Finally, the estimates x(k + 1|k + 1) are further im-

proved by the use of the Kalman smoother (Shumway

and Stoffer, 2000).

2.4 The Viterbi based algorithm

The Viterbi algorithm has been introduced in (Viterbi,

1967). A good description is also given in (Forney Jr.,

1973). It has been recommended for tracking puncti-

form targets in clutter in (Quach and Farooq, 1994)

and for tracking extended targets in (Kr

außling et al.,

2004a).

Whereas the Kalman ﬁlter algorithm (KFA) uses all

measurements in the validation gate as an unweighted

mean, the Viterbi based algorithm (VBA) calculates a

separate estimate x(k + 1|k + 1)

for every selected

measurement z

k+1,i

with i = 1, . . . , m

k+1

. There-

fore it uses a directed graph. The nodes of this graph

are the measurements in the validation gates or the

ICINCO 2005 - ROBOTICS AND AUTOMATION

128

selected measurements. Given the selected measure-

ments

= {z

k,j

}

j=1

at time step k the selected

measurements for the time step k + 1 are determined

as follows: for every selected measurement z

k,j

the

prediction y(k + 1|k)

is calculated based on the esti-

mate x(k|k)

. Then the corresponding validation gate

is applied to the measurements of time k + 1. This

results in a set

k+1,j

of measurements which have

passed the particular validation gate for the measure-

ment z

k,j

successfully. The set

k+1

of selected mea-

surements at time k + 1 is then just the union of these

sets, i.e.

k+1

= ∪

k+1,j

. (17)

k+1,j,i

, the distance between the nodes z

k,j

and

k+1,i

, is calculated using the formula

k+1,j,i

⊤

k+1,j,i

k+1

]

−1

k+1,j,i

+ ln



|2πS

k+1



. (18)

Thereby ν

k+1,j,i

is the innovation deﬁned as

k+1,j,i

= z

k+1,i

− y(k + 1|k)

. (19)

k+1

and y(k + 1|k)

are the innovation covariance

respectively the previously deﬁned prediction evalu-

ated by the Kalman ﬁlter, based on the nodes Z

k,j

l,i(l,j)

}

l=1

belonging to the path ending in z

k,j

Thereby, the set Z

k,j

is called the tracking history be-

longing to the node z

k,j

(see below). The predecessor

of the node z

k+1,i

is that node z

k,j

which minimises

the length d

k,j

+ a

k+1,j,i

of the corresponding path in

the graph. For this purpose only those measurements

k,j

whose gates have been passed by z

k+1,i

success-

fully are considered (Pulford and Scala, 1995). The

corresponding index is referred to as j(k, i). The

length d

k+1,i

of the path ending in z

k+1,i

is then

received as d

k,j(k,i)

+ a

k,j(k,i),i

. Thus by a recur-

sive algorithm for every selected measurement at time

k + 1 the tracking history Z

k+1,i

is determined. Next,

a Kalman ﬁlter is applied to calculate an estimate

x(k + 1|k + 1)

for the measurement z

k+1,i

using the

prediction y(k + 1|k)

j(k,i)

as the input in formula 14.

For further details of the algorithm please see refer-

ences (Kr

außling et al., 2004a) and (Kr

außling et al.,

2004b). Finally, when the last scan is reached, the

tracking history with the shortest length of the path

is chosen and the corresponding estimates are used

as the estimates for the state and the position respec-

tively of the object. As in the case of the KFA, these

estimates are further improved by use of the Kalman

smoother.

3 EVALUATION OF THE

ALGORITHMS

Unfortunately, a detailed evaluation of the algorithms

with respect to accuracy and need for computation

time is beyond the scope of a conference paper. So

we would like to point out just the main results gained

from simulated data: the KFA outmatches the VBA

in terms of both criterions. For the comparison of

the algorithms we used simulated data of an exem-

plary problem. Thereby, a circular object with radius

27 cm moves on a circle with radius d around the ob-

serving robot. The radius d has been varied from 1 m

to 8 m and the standard deviation of the laser mea-

surements has been varied from 1 cm to 10 cm. Simu-

lated data have been used, because we needed to know

the true position of the target very accurately, a goal

which is hard to achieve using data from a real ex-

periment. This case has already been mentioned by

other authors (Zhao and Shibasaki, 2005). The val-

ues used for the distance and the standard deviation of

the measurement noise are typical for real objects ob-

served with a Sick laser. The values for the distance

between the estimated position and the true position

of the object are in the range of 1 cm for the KFA,

whereas they are in the range of 20 cm for the VBA.

The computing time needed for one computation step

of the KFA is approximately 20 ms, whereas it is in

the range from 70 ms to 1.5 s for the VBA depending

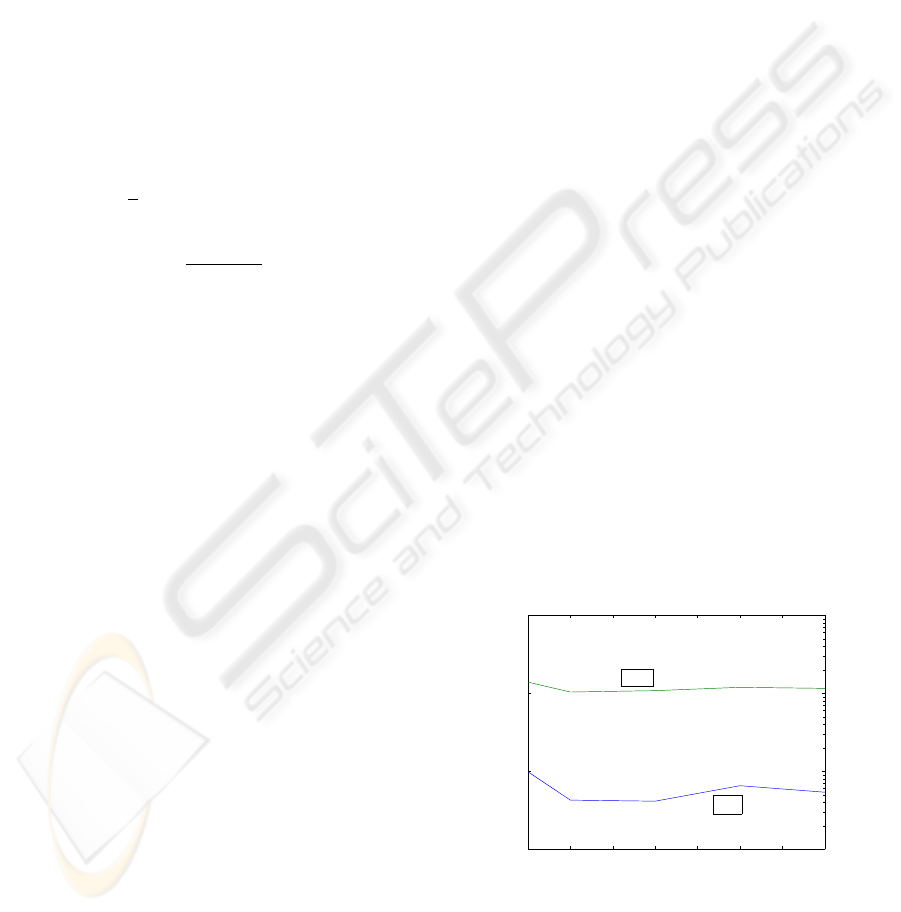
on the distance of the observed object. Figures 2 and

3 show the results for the standard deviation of 5 cm

of the laser measurements. The results for the other

standard deviations are similar. Please note the loga-

rithmic scaling of the ordinates. Further details are

100 200 300 400 500 600 700 800

−1

radius d in cm

distance in cm

distance from the true position

VBA

KFA

Figure 2: Comparison of the distances from the true posi-

tion.

given in a technical report published by the authors

(Kr

außling et al., 2005).

A SWITCHING ALGORITHM FOR TRACKING EXTENDED TARGETS

129

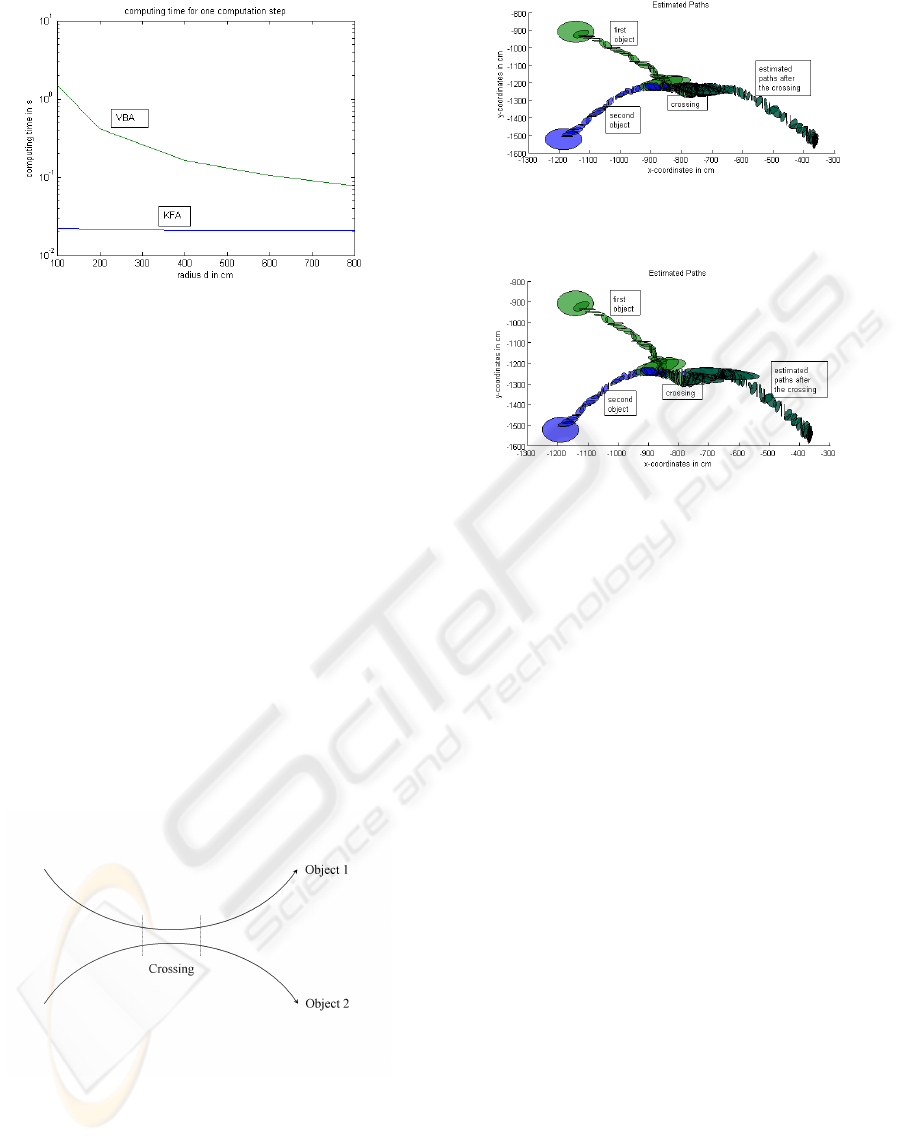
Figure 3: Comparison of the computing time.

4 THE PROBLEM OF CROSSING

TARGETS

The crossing of two targets means that the validation

gates of two targets intersect, i.e. some measurements

are lying in the validation gates of both of the two

targets. Figure 4 shows a typical situation.

Figures 5 and 6 show the behaviour of the two in-

troduced algorithms when being applied to the prob-

lem of crossing targets using real data originating

from an experiment with two walking persons in our

laboratory. They show the estimates for the position

of the objects calculated by the two algorithms by use

of ellipses. Thereby the estimated position is the cen-

tre of the ellipse, whereas the shape of the ellipse rep-

resents the actual geometry of the tracked object. The

objects start in the left and move to the right as indi-

cated in ﬁgure 4.

Figure 4: Two crossing objects.

Obviously none of the algorithms can deal with the

problem of crossing targets. They all locate both ob-

jects at the same position after the crossing. This

behaviour is common to other algorithms for track-

ing extended targets developed so far by our research

Figure 5: Application of the KFA to crossing targets, real

data.

Figure 6: Application of the VBA to crossing targets, real

data.

group, for instance an EM (Expectation Maximisa-

tion) based algorithm (Stannus et al., 2004). Thus,

we have developed an improved algorithm based on

the VBA that can deal with the problem of crossing

targets (Kr

außling et al., 2004a). It uses the fact, that

the VBA is able to cope with multimodal densities to

some degree. This feature is due to the fact, that the

VBA calculates separate validation gates and state re-

spectively position estimates for every selected mea-

surement. The handling of multimodal densities is a

characteristic that the VBA algorithm has in common

with the SJPDAF algorithm (Schulz et al., 2001). But

while this algorithm uses particle ﬁltering (Gordon

et al., 1993), (Pitt and Shephard, 1997) and thus has to

deal with several hundreds of particles, the Viterbi al-

gorithm only handles a few points or state estimates.

Additionally, these points contain some information

about the geometry of the tracked object as proposed

in (Kr

außling et al., 2004a). When a crossing between

two targets occurs the VBA shows the following be-

haviour: as soon as the crossing takes place the al-

gorithm tracks all points originated from both objects

simultanously. When the crossing is over, these points

are again separated into two distinct clusters of points

and these clusters are still tracked simultaneously for

both objects. Only the assignment of the clusters to

the objects is wrong, since in most cases one cluster

is associated to both objects by the VBA algorithm at

the end of the tracking process like in ﬁgure 6. Our

new approach is based on these observations. It uses

the results of the VBA and furthermore performs the

ICINCO 2005 - ROBOTICS AND AUTOMATION

130

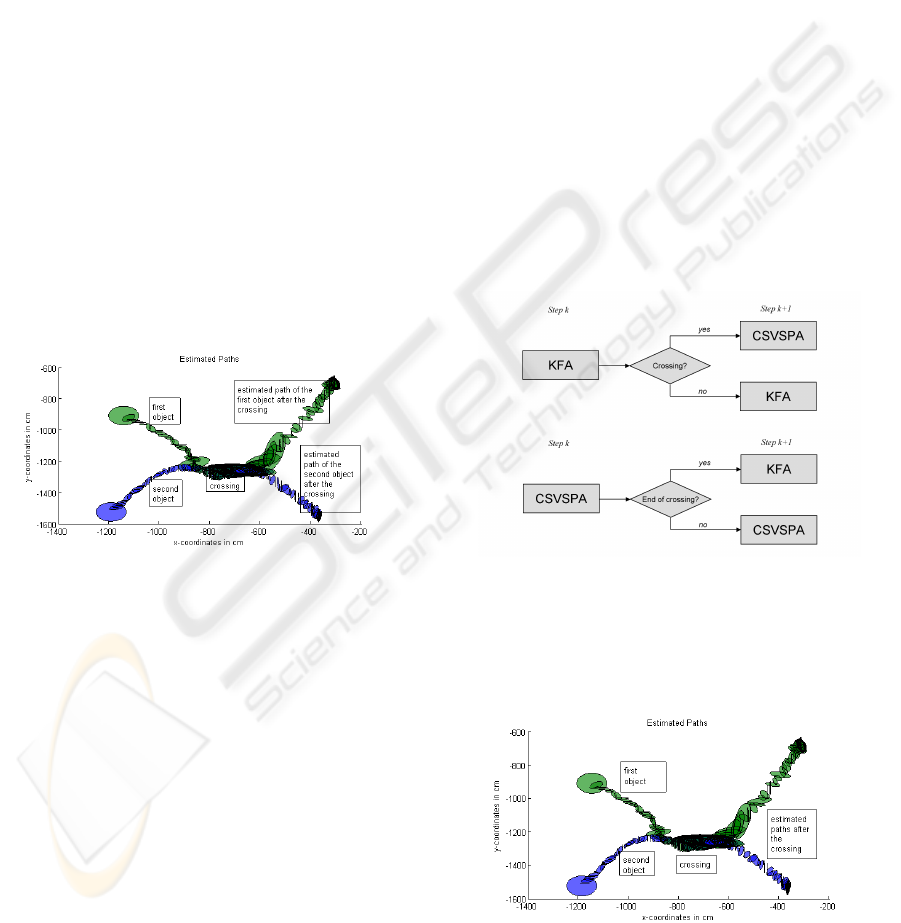
following three distinct steps:

1. At every time step k for every pair of targets it is

tested, if a crossing has started to take place. This

is supposed to be the case when at least one mea-

surement lies in the validation gates of both of the

two objects.

2. Once a crossing between two objects has been de-

tected, at each following time step it is examined

wether the crossing has ﬁnished, which means that

there are two separated clusters.

3. As soon as the end of the crossing has been ob-

served the two associated clusters are assigned to

the two corresponding targets.

The three steps are carried out based on geometrical

considerations and can be viewed under the super-

ordinate concept of data mining (Han and Kamber,

2001). Finally, like for the VBA at the end of the

tracking process for each object the path with the min-

imum length is determined and a Kalman smoother is

applied. This improved algorithm is called Cluster

Sorting Viterbi Shortest Path Algorithm (CSVSPA).

For further details see (Kr

außling et al., 2004b). Fig-

ure 7 shows the application of the CSVSPA to the pre-

viously used data.

Figure 7: Crossing targets, handled by the CSVSPA, real

data.

Of course it could be argued that there are already

well established algorithms for tracking crossing tar-

gets like the JPDAF (Fortmann et al., 1983) or the

Multiple Hypothesis Filter (Reid, 1979). But these

algorithms have been developed for tracking puncti-

form targets in clutter and probably will fail when

tracking extended targets. There might be several

measurements from the same extended target. Thus

two different measurements from the same target can

be associated with the two targets. But the exclusion

of the association of measurements from the same tar-

get to both objects is the essential core of these two

algorithms. Thus they will fail to separate the two tar-

gets after the crossing in most of the cases, especially

when an additional occlusion takes place. In most of

the cases the two tracks will coincide after the cross-

ing like for the VBA in ﬁgure 6. Moreover the compu-

tational burden for applying these algorithms is very

high when applied to extended targets, since these ob-

jects can be the origin of up to ten measurements.

5 A NEW SWITCHING

ALGORITHM

Since the CSVSPA is able to deal with crossing tar-

gets it could, of course, be used for the whole track-

ing process. But since this algorithm is based on the

VBA algorithm it is not as accurate as the KFA as

long as no crossing takes place and needs much more

computation time. Therefore, we developed a new

switching or hybrid algorithm (SA), which uses the

CSVSPA only when a crossing takes place. For the

rest of the time it uses the very accurate and fast KFA.

This choice is also motivated by the fact, that the KFA

is faster and more accurate than other algorithms de-

veloped by our research group for tracking extended

objects (Kr

außling et al., 2005). Thereby, crossings

are detected as in the case of the CSVSPA. Figure 8

shows the ﬂowchart of the SA.

Figure 8: Flowchart of the new switching algorithm.

Figure 10 shows that the SA can deal with crossing

targets as well as the CSVSPA using the data from

the last section. To illustrate the power of the SA fur-

Figure 9: Crossing targets, handled by the new switching

algorithm, real data.

ther experiments with real data have been carried out.

A SWITCHING ALGORITHM FOR TRACKING EXTENDED TARGETS

131

Thereby two humans were walking around in our lab-

oratory. The measurements were recorded with two

SICK lasers each of them with a 180 degree ﬁeld of

view mounted on a mobile robot. The evaluation of

the algorithms was performed by means of ﬁve sim-

ilar scenarios. In each scenario two persons walked

separately for some time interval t

at the beginning

of the experiment. Then the persons met each other

and walked together for some time interval t

, so that

a crossing took place. Finally, the persons split again

and walked alone for the time interval t

. Thereby,

the time interval t

was arranged to be approximately

30 seconds for each scenario. Furthermore, the time

intervals t

and t

were of same length for each run

varying from 30 seconds to 150 seconds. Figure 11

shows an example of the results for the estimated

paths using the SA. Like in section 4 KFA and VBA

Figure 10: Crossing targets, real data of scenario 1, handled

by the new SA.

always failed, whereas CSVSPA and SA behaved well

for all ﬁve scenarios.

Table 1 describes the results for the needed com-

puting time. It contains the average time t

needed

for the calculations of one time step in milliseconds.

Table 1: Average Computing Time

scenario 1 2 3 4 5

KFA 54.1 53.8 54.6 53.9 54.4

VBA 379.0 355.7 478.6 366.3 469.3

CSVSPA 294.3 258.6 329.5 260.7 320.3

HA 171.3 123.7 119.2 110.8 91.5

The table shows the improvement that can be

achieved using the SA in comparison to the CSVSPA.

Moreover, with growing intervals t

and t

the gain

increases rapidly.

6 CONCLUSIONS

In this paper we have addressed the problem of track-

ing extended targets. Two basic algorithms for the

tracking process have been introduced: they are either

just using the Kalman ﬁlter (KFA) or additionally the

Viterbi algorithm (VBA). The comparison of the al-

gorithms has shown that the KFA is much faster and

much more accurate than the VBA. Thereafter, the

problem of two crossing targets has been introduced.

It has been shown that both algorithms produce in-

sufﬁcient results under the constraints of crossing tar-

gets. Thus an enhancement of the VBA in form of

the CSVSPA has been proposed, which can deal with

crossing targets. But since the CSVSPA is based on

the VBA and thus is imprecise and slow, we ﬁnally

developed the SA, which makes use of the CSVSPA

only when a crossing has been detected and otherwise

uses the KFA. The power of the SA has been demon-

strated on real data. Thereby, it has been shown,

that the SA can handle crossing targets as well as the

CSVSPA but needs much less computing time.

In the future we will try to generalise our method

for tracking crossing objects from the case of two ob-

jects to n objects (multi target tracking). Furthermore,

the SA should be compared to the well established al-

gorithms like the SJPDAF (Schulz et al., 2001). Fi-

nally, the calculation of the Kalman gains should be

substituted by the calculation of the limit as men-

tioned above to make the algorithm useable in real

time applications.

REFERENCES

Bar-Shalom, Y. and Fortmann, T. (1988). Tracking and

Data Association. Academic Press.

Crowley, J. L. (1989). Control of translation and rotation in

a robot vehicle. IEEE Iros–II, Tsukuba, Japan.

Dissanayake, G. M. W. M., Newman, P., Clark, S., Durrant-

Whyte, H., and Csorba, M. (2001). A solution to

the simultaneous localization and map building (slam)

problem. IEEE Transactions on Robotics and Au-

tomation, 17:229–241.

Ekstrand, B. (1983). Analytical steady state solution for

a kalman tracking ﬁlter. IEEE Trans. Aerospace and

Electronic Systems, AES–19:815–819.

Fod, A., Howard, A., and Mataric, M. J. (2002). Laser–

based people tracking. In Proceedings of the IEEE

Intl. Conf. on Robotics and Automation, pages 3024–

3029.

Forney Jr., G.-D. (1973). The viterbi algorithm. Proceed-

ings of the IEEE, 61(3):268–278.

Fortmann, T. E., Bar-Shalom, Y., and Scheffe, M. (1983).

Sonar tracking of multiple targets using joint prob-

abilistic data association. IEEE Journal of Oceanic

Engineering, OE–8(3).

Fuerstenberg, K. C., Linzmeier, D. T., and Dietmayer, K.

C. J. (2002). Pedestrian recognition and tracking of

vehicles using a vehicle based multilayer laserscan-

ner. In Proceedings of IV 2002, Intelligent Vehicles

Symposium, volume 1, pages 31–35.

Gordon, N., Salmond, D., and Smith, A. (1993). A novel

approach to nonlinear/non–gaussian bayesian state es-

timation. IEE Proceedings F, 140:107–113.

ICINCO 2005 - ROBOTICS AND AUTOMATION

132

Guivant, J. and Nebot, E. (2001). Navigation in large out-

door unstructured environments. International Sym-

posium of Robotics Research.

Gutmann, J.-S., Burgard, W., Fox, D., and Konolige, K.

(1998). An experimental comparison of localization

methods. In International Conference on Intelligent

Robots and Systems (IROS 1998), Victoria, Canada.

Gutmann, J.-S. and Fox, D. (2002). An experimental com-

parison of localisation methods continued. In Pro-

ceedings of the IEEE/RSJ International Conference

on Intelligent Robots and Systems (IROS 2002), Lau-

sanne, Switzerland.

Han, J. and Kamber, M. (2001). Data Mining. Academic

Press, London.

Kalata, P. R. (1984). The tracking index: A general-

ized parameter for alpha–beta–gamma target trackers.

IEEE Trans. Aerospace and Electronic Systems, AES–

20:174–182.

Kalman, R. E. (1960). A new approach to linear ﬁltering

and prediction problems. Trans. ASME, J. Basic En-

gineering, 82:34–45.

außling, A., Schneider, F. E., and Wildermuth, D.

(2004a). Tracking expanded objects using the viterbi

algorithm. In Proceedings of the IEEE Conference on

Intelligent systems, Varna, Bulgaria.

außling, A., Schneider, F. E., and Wildermuth, D.

(2004b). Tracking of extended crossing objects us-

ing the viterbi algorithm. In Proceedings of the 1st

International Conference on Informatics in Control,

Automation and Robotics (ICINCO).

außling, A., Schneider, F. E., and Wildermuth, D. (2005).

Zur verfolgung ausgedehnter ziele — eine

ubersicht

uber ausgew

ahlte algorithmen und ein vergleich deren

ute. Technical report, FKIE/FGAN, Wachtberg, Ger-

many.

Leonard, J. J. and Durrant-Whyte, H. F. (1992). Directed

Sonar Sensing for Mobile Robot Navigation. Kluwer

Academic Publishers.

Mahalanobis, P. C. (1936). On the generalized distance in

statistics. Proceedings of the National Institute of Sci-

ence, 12:49–55.

Pitt, M. and Shephard, N. (1997). Filtering via simulation:

auxiliary particle ﬁlters. Journal of the American Sta-

tistical Association.

Prassler, E., Scholz, J., and Elfes, E. (1999). Tracking peo-

ple in a railway station during rush–hour. In Chris-

tensen, H. I., editor, Computer Vision Systems, vol-

ume 1542, pages 162–179. Springer, lecture notes in

computer science edition.

Pulford, G. W. and Scala, B. L. (1995). Over–the–horizon

radar tracking algorithm using the viterbi algorithm

— third report to high frequency radar division. Tech-

nical Report 27/95, Cooperative Research Centre for

Sensor Signal and Information Processing, University

of Melbourne.

Quach, T. and Farooq, M. (1994). Maximum likelihhod

track formation with the viterbi algorithm. In Pro-

ceedings of the 33rd Conference on Decision and

Control, Lake Buena Vista, Florida.

Reid, D. B. (1979). An algorithm for tracking multiple tar-

gets. IEEE Trans. Automatic Control, AC–24:843–

854.

Schulz, D., Burgard, W., Fox, D., and Cremers, A. B.

(2001). Tracking multiple moving objects with a mo-

bile robot. In Proceedings of the 2001 IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition (CVPR 2001).

Shumway, R. H. and Stoffer, D. S. (2000). Time Series

Analysis and Its Applications. Springer.

Stannus, W., Koch, W., and Kr

außling, A. (2004). On

robot–borne extended object tracking using the em al-

gorithm. In Proceedings of the 5th Symposium on In-

telligent Autonomous Vehicles, Lisbon, Portugal.

Taylor, G. and Kleeman, L. (2004). A multiple hypothesis

walking person tracker with switched dynamic model.

In Proceedings of the Australasian Conference on Ro-

botics and Automation, Canberra, Australia.

Thrun, S. (1998). Learning metric-topological maps for in-

door mobile robot navigation. Artiﬁcial Intelligence,

99(1):21–71.

Thrun, S., Fox, D., and Burgard, W. (1999). Markov lo-

calization for mobile robots in dynamic environments.

Journal of Artiﬁcial Intelligence Research, 11:391–

427.

van Keuk, G. (1971). Zielverfolgung nach kalman–

anwendung auf elektronisches radar. Technical Report

173, Forschungsinstitut f

ur Funk und Mathematik,

Wachtberg–Werthhoven, Germany.

Viterbi, A. J. (1967). Error bounds for convolutional codes

and an asymptotically optimum decoding algorithm.

IEEE Transactions On Information Theory, IT–13(2).

Zhao, H. and Shibasaki, R. (2005). A novel system

for tracking pedestrians using multiple single–row

laser–range scanners. IEEE Transactions on Systems,

Man and Cybernetics—Part A: Systems and Humans,

35(2):283–291.

A SWITCHING ALGORITHM FOR TRACKING EXTENDED TARGETS

133