A NEW ART GALLERY ALGORITHM FOR SENSOR

LOCATION

Andrea Bottino, Aldo Laurentini

Dipartimento di Automatica e Informatica, Politecnico di Torino, Corso Duca degli Abruzzi 24, Torino, Italy

Keywords: Art gallery, sensor positioning, planning, surveillance.

Abstract: Locating sensors in2D can be often modeled as an Art Gallery problem. Unfortunately, this problem is NP-

hard, and no finite algorithm, even exponential, is known for its solution. Algorithms able to closely

approximate the optimal solution and computationally feasible in the worst case are unlikely to exist.

However this is an important problem and algorithms with “good” performance in practical cases are sorely

needed. After reviewing the available algorithms, we propose a new sensors location incremental technique.

The technique converges toward the optimal solution. It locally refines a starting approximation provided by

an integer covering algorithm, where each edge is observed entirely by at least one sensor. A lower bound

for the number of sensor, specific of the polygon considered, is used for halting the algorithm, and a set of

rules are provided to simplify the problem.

1 INTRODUCTION

A number of computer vision tasks, as inspection,

surveillance, image based rendering, constructing

environment models, require multiple sensor

locations, or the displacement of a sensor in multiple

positions.

Sensor placement is an active area of research. A

recent survey (Scott and Roth, 1992) refers in

particular to tasks as reconstruction and inspection.

Several other tasks and techniques were considered

in the more seasoned surveys (Tarabanis et al., 1995,

Newman and Jain, 1995). Practical sensor planning

problems require considering a number of

constraints, such as image resolution, field of view

of the sensors, feature visibility, lighting, etc.

Visibility is clearly the fundamental constraint for

any kind of task and optical sensor. The sensor is

usually modeled as a point and referred to as a

“viewpoint”. A feature of an object is said to be

visible, or not occluded, from the viewpoint if any

segment joining a point of the feature and the

viewpoint does not intersects the environment or the

object itself.

Although in general the problem is three-

dimensional, in some cases it can be restricted to 2D.

This is for instance the case of buildings, which can

be modeled as objects obtained by extrusion.

For omni directional or rotating sensors, the 2D

visibility can be modeled as an Art Gallery problem,

which asks to position a minimum set of “guards” in

a polygon. Unfortunately, the problem, as well as

several of its variations, is NP-hard, and no finite

algorithm, not even exponential, for locating a

minimum set of guards is known. In addition,

algorithms computationally feasible in the worst

case and able to closely approximate the optimal

solution are unlikely to exist (Eidenbenz et al.,

2001). However, this is an important practical

problem and approximate algorithms

computationally feasible and supplying satisfactory

solutions in practical cases are sorely needed.

In this paper, after discussing the available

algorithms, we present a new approximate sensor

positioning techniques. The algorithm is incremental

and converges toward the optimal solution. It makes

use a lower bound, specific of the polygon

considered, for the number of sensors, and of rules

for locally refining a starting approximate solution.

This solution is provided by an integer covering

algorithm, where each edge must be observed

entirely by one sensor at least. The proposed

technique can also take into account constraints as

range and incidence.

242

Bottino A. and Laurentini A. (2005).

A NEW ART GALLERY ALGORITHM FOR SENSOR LOCATION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 242-249

DOI: 10.5220/0001174002420249

 SciTePress

2 ART GALLERY PROBLEMS

AND EDGE COVERING

The original problem, stated in 1975, refers to the

surveillance, or “cover” of polygonal areas. The

famous Art Gallery Theorem stated the upper tight

bound ⎣n/3⎦ for the minimum number of “guards”

(omni directional sensors) for covering any polygon

with n edges, metaphorically the interior of an art

gallery. The upper tight bound ⎣(n+h)/3⎦ holds for

polygons with n edges and h holes. Many variations

of the problem have been considered, and much

work has been done for finding bounds in these

cases. The decision problems related to the original

problem (are k guards sufficient for covering a given

polygon?), as well as those related to several similar

problems, has been found to be NP-hard (Danner

and Kavraki, 2002). No exact finite algorithm for

locating a minimum set of sensors is known. For

further details, the reader is referred to the

monograph of O’Rourke (1987), and to the surveys

of Shermer (1992) and Urrutia (2000).

Sensors positioning problems usually deals with

observing, or covering, the boundary of objects and

environment. Then in 2D we are content with

observing the edges of a polygonal environment. We

call this the Edge Covering (EC) problem, and the

classic problem the Interior Covering (IC) problem.

The EC problem and its relation with IC have been

analyzed in Laurentini, 1999. For both EC and IC,

the worst-case number of guards for polygons with

and without holes is the same, but an optimum set of

IC guards is not in general an optimum set of EC

guards and vice-versa, and no simple rule, as adding

or deleting guards, seems to exists for transforming

an optimal solution of one problem in an optimal

solution of the other. Also the decision problem

associated to EC is NP-hard, since the classic proofs

for polygons with and without holes also hold for

edge covering (Laurentini, 1999). As for IC, at

present no finite exact algorithm is known for

locating a minimum set of EC guards in a given

polygon.

In addition, recent result (Eidenbenz et al., 2001)

shows that no worst-case computationally feasible

approximate algorithm able to find solution close to

the optimum is likely to exist. These results apply to

both EC and IC, as well as to others problems in the

area.

Finally, let us observe that the apparently continuous

nature of EC (and IC) prevents putting the problems

in the class NP. On this point, see also O’Rourke

and Supowitz, 1983.

In the following section we will discuss the

approximate algorithms existing for EC.

3 EXISTING APPROXIMATED

EDGE COVERING

ALGORITHMS

Some approximate seasoned algorithms for IC are

reported in Shermer, 1992. All these algorithms are

polynomial. It can be easily seen that their

performance in relation with the optimal solution

can be as bad as possible (O(n) guards, where n is

the number of edges, when O(1) are sufficient).

These algorithms have not been implemented, and

no experimental results comparing the average

performances of these algorithms with the optimal

solution have been presented. Anyway, we have

seen that in general the optimal EC and IC covers

are different.

More recently, some attempt has been made for

constructing practical sensor positioning algorithms.

Kazakakis and Argyros (2002) have proposed a

heuristic that divides the polygon into a number of

convex polygons, each of which can be inspected by

a guard with visibility range restriction. The

algorithm has been implemented and some

experimental results have been reported. Time

performances are good, but the authors do not

discuss how far are the solutions from optimum.

The randomized approach (Danner and Kavraki,

2002, Gonzales-Banos and Latombe, 1998 and

2001), appears the main practical technique

available. We discuss here the most recent (not

implemented) randomized algorithm of Gonzales-

Banos and Latombe (2001), which also takes into

account range and incidence constraints. The

algorithm is as follows. First, the authors observe

that, given an optimal solution for locating the

guards, perturbing the positions of the guards into

sufficiently small areas does not affect optimality.

This leads to a randomized approach, where a

number of viewpoints are located at random in the

polygon, hoping of locating some points sufficiently

near the points of an optimal solution. The next step

consists in dividing the polygon boundaries into

cells such that each viewpoint sees exactly a set of

these cells. Selecting a minimal set of points among

the random points is equivalent to solve an NP-

complete set-covering problem. It is known that a

greedy solution is polynomial, but has an

approximation ratio bounded by (1+lgp), where p is

the cardinality of the largest subset. It is clear that

A NEW ART GALLERY ALGORITHM FOR SENSOR LOCATION

243

this factor is not a strong guarantee of good

approximation for polygons with many edges and

holes, since p is O(m(n+h)), where m is the number

of random point, which is assumed to be rather large

and in any case much larger than n. However, a

clever exploitation of the particular set structure

makes it possible to reduce the problem within an

approximation ratio of (1+ q), where q is

O(lg(n+h)

·lg(clg(n+h)) and c is the optimal size.

The advantage is that q does not depend on the

presumably large number of random points.

Concluding, the authors obtain an algorithm

polynomial in the worst-case, at the expense of the

closeness to the optimal solution. In fact, also the

improved approximation factor can be large for

polygons with hundreds of edges and some tens of

holes. In addition, it is clear that a main problem

with this algorithm is the density of the sampling, “a

choice that is perhaps more a craft than a science”

according to the authors themselves. An incremental

algorithm could be developed adding new random

points, but we have no idea of the closeness to

optimum of the solution, and we do not know where

is more convenient to add new samples.

4 WHAT AN APPROXIMATE

PRACTICAL ALGORITHM

SHOULD DO

The performance of a “good” or “practical” Art

Gallery algorithm should be analyzed in terms of

both running times and closeness to the optimal

solution of the approximation obtained. Since we

deal with a problem that we are not even able to put

in NP, we cannot be too exigent regarding the worst

case behavior, being satisfied with algorithms

capable of running in practical cases, in reasonable

times. Clearly, running time depends on the number

of edges and on the shape of the polygon. We can

assume that a reasonable choice to model many

practical environments or 2D objects is to consider

polygons with several tens, or some hundreds, of

edges. As for shape, the algorithm should be tested

with examples of real environments.

Another desirable feature of a practical algorithm is

the possibility of approaching the optimal solution

by refining an initial approximation, at the expense

of computation time. For obtaining a balanced

trade-off between precision and time, we should

have:

• some information about the quality of the

approximation obtained at each step, which

can be used to decide whether to stop the

algorithm

• an incremental algorithm, able to refine

locally the solution of the previous step.

The purpose of this paper is to present an algorithm

that, to some degree, fulfills the previous

requirements of a “good” or “practical” algorithm.

Even if we are not able to discretize an apparently

continuous problem, we propose an incremental

algorithm, able to refine locally the solution, and we

also provide a lower bound, specific of the case

considered, that can be used to decide when to stop

the incremental process. The algorithm starts with an

initial approximation supplied by an integer edge

covering algorithm.

5 INTEGER EDGE COVERING

The Integer Edge Covering (IEC) problem is a

useful restriction of EC, requiring each edge to be

entirely covered by at least one guard. For some

practical task, observing entirely a feature of an

object, usually modeled as an edge in 2D, could be

preferable. In addition, for several not particularly

tricky polygons the optimal unrestricted solution

appears not too far from an optimal integer cover.

For these reasons, integer covering is the starting

approximation of our unrestricted edge-covering

algorithm. A simple example showing the difference

between EC and IEC is shown in Fig.1

Figure 1: Two EC sensors cover the interior boundary of

the polygon, but three IEC sensors are required

Bounds for IEC have been discussed in Laurentini,

1999. Regarding complexity, it is easy to see that the

reductions of 3-SAT (O’Rourke, 1987) for polygons

with and without holes also hold for IEC, since both

reductions construct polygons where the edges are

observed entirely by at least one guard. Thus, also

the decision problem associated to IEC is NP-hard.

The difference is that the restriction allows putting

the problem in NP, so that it becomes NP-complete

and finite algorithms are possible. In fact, the

polygon can be divided into a set of non-overlapping

zones, such that each point in each zone covers

entirely the same set of edges. Then an hypothesis of

solution consists in a finite string of characters that

specifies a particular subset of these zones.

ICINCO 2005 - ROBOTICS AND AUTOMATION

244

An algorithm for finding a set of zones where

locating a minimum set of guards is reported in

Laurentini, 1999. A modified version of this

algorithm has been implemented in Bottino and

Laurentini, 2004. The algorithm works for any

polygonal environment (external coverage of

multiple polygons, internal coverage of polygons

with or without holes). Referring the readers to the

original paper for details, the main steps of the

algorithm are as follows:

IEC Algorithm

Step 1. Compute a partition Π of the viewing space

into regions Z

such that:

1. The same set E

of edges is entirely visible

from each point of Z

, ∀i. Actually, each

region is also labeled with the partially

visible edges and the number of occlusions.

2. The regions Z

are maximum regions, that is

⊄ E

where Z

is any region contiguous

to Z

Step 2. Select the dominant regions and the essential

regions. A region Z

is dominant if there is no other

region Z

such that E

⊂ E

. An essential zone is a

dominant zone that covers an edge not covered by

any other dominant zone.

Step 3. Find an optimum set of zones covering all

the edges. This is a set covering problem restricted

to the set of edges not covered by the essential

zones, and to the subsets corresponding to the

dominant zones that: a) are not essential; b) cover

some edge not already covered by the essential

zones.

Steps 1 and 2 are polynomial (Laurentini, 1999);

Step 3 is exponential in the worst case. However, in

many cases the simplifications introduced by

dominant and essential zones strongly reduce the

complexity of the algorithm. Observe that the

algorithm does not provide in general all the

possible minimal sets of zones, since there could be

solutions including non-dominant zones. However,

this does not seems a serious drawback, since each

non-dominant zone can be replaced by a dominant

zone that covers some more edges, and multiple

coverage in several practical cases is preferable, for

instance in case of sensor failure.

6 THE SENSOR POSITIONING

ALGORITHM

Integer edge covering provides a starting

approximation, which can be incrementally refined

for approaching the optimal unrestricted solution.

For deciding if a solution is acceptable, we compute

a lower bound LB(P) for the optimum number of

sensors, specific of the polygon P considered. If the

starting solution is far from the lower bound, we can

improve this solution by splitting some of the edges

and re-applying the IEC algorithm. It is clear that

this procedure converges toward the optimal

solution, if computationally feasible. For reducing

the computational burden, we also supply rules that

tell us which edges must not be divided in order to

reach the optimal solution. Summarizing, our sensor

positioning algorithm works as follows.

Given a polygon P, compute the lower bound LB(P)

with the LBA algorithm described in section 6.2

Apply the IEC algorithm and find an approximate

covering. Compare the cardinality CA of the

approximate covering with the lower bound. If they

are equal, the solution is optimal also for the

unrestricted problem. If (CA/LB(P))<1+ε, where ε is

some predefined threshold, stop; otherwise:

Apply the algorithm INDIVA, described in section

6.3 for finding the edges that must not be divided,

split the others and return to 2

Actually, it could be necessary to stop the

algorithm before reaching a satisfactory cover due to

the computation time. In the rest of this section we

describe the algorithms INDIVA and LBA.

6.1 Integer and weak visibility

polygons

Both algorithms LBA and INDIVA make use of the

concept of weak and integer visibility polygons of

the edges (J. O'Rourke, 2002). Let us briefly recall

their definitions:

the Weak visibility polygon W(e

) of an edge e

is the

polygon whose points see some points of e

the Integer visibility polygon I(e

) is the polygon

whose points see entirely e

An example is shown in

Fig.2

Figure 2: The integer and weak visibility polygons of the

edge e

Polynomial algorithms for computing weak and

integer visibility polygons of an edge are described

in the literature (Sack and Suri, 1990). In our case

however, both polygons can be computed as a

byproduct of the IEC algorithm. If there are p zones

A NEW ART GALLERY ALGORITHM FOR SENSOR LOCATION

245

in the partition Π, computing the visibility polygons

for all edges is O(pn).

6.2 LBA, the Algorithm for Finding

a Lower Bound

LBA Algorithm finds a maximum subset of disjoint

(not intersecting) weak visibility polygons W(e

The cardinality of this set is LB(P).

Since each weak visibility polygon must contain at

least one sensor, no arrangement of EC sensors can

have fewer sensors than LB(P). A simple example is

shown in Fig.3, where the lower bound is 2.

Figure 3: A maximum set of non-intersecting weak

visibility polygons

Computing the lower bound requires solving the

maximum independent set problem for a graph G

where each node represents the weak visibility

polygon of an edge of P, and each edge of G

connects nodes corresponding to intersecting weak

visibility polygons. The problem is equivalent to the

maximum clique problem for the complement graph

G’ (the graph obtained by joining those pairs of

vertices that are not adjacent in G). It is well known

that these are NP-complete problems.

However, we stress that exact branch-and-bound

algorithms for these problems have been presented

and extensively tested (Woods, 1997, Oestergard,

2002), showing more than acceptable performance

for graphs with hundreds of nodes. Then, we assume

that computing LB(P) is computationally feasible for

the practical cases considered.

6.3 INDIVA, the Algorithm for

Finding Indivisible Edges

In this section we describe a set of rules for finding

the indivisible edges of P. An edge is called

indivisible if optimal sets of sensors exist such that

edge is entirely observed by at least one sensor.

Clearly, for approaching these optimal solutions we

do not need to split these edges. The first two rules

are as follows:

Rule1. If W(e

) = I(e

), e

is indivisible.

Rule2. If W(e

) ⊆ I(e

), e

is indivisible.

Both rules follows from the fact that at least one

sensor of any minimum set must be located in each

weak visibility polygon, and then also in the integer

visibility polygon satisfying one of the above rules.

A simple example will show how to apply these

rules, and that they can be powerful tools for

simplifying the problem. Let us consider the

polygon in fig. 2(a).

Figure 4: In this case, the optimum EC and IEC covers are

equal

The weak visibility polygon of e

is shown in (b). It

is coincident (c) with the integer visibility polygon

I(e

), and then for Rule 1 e

is indivisible, and

marked with a thicker line. In (d) it shown that I(e

W(e

), and then for Rule 2 also e

is indivisible, as

well as, for similar reasons, e

and e

. As for e

, it is

indivisible, since W(e

)= I(e

) (Fig.1 (e). Finally, in

(f) it is shown I(e

). Since I(e

)⊃W(e

), also e

indivisible.

Concluding, in this example the unrestricted

minimal set of guards is that provided by the integer-

covering algorithm. The same result could have been

obtained by computing the IEC solution, whose

cardinality is equal to the lower bound LB(P). This

also happens for any polygon of the family shown in

(g), which is used for showing that the bound

supplied by the Art Gallery theorem is tight.

We stress that if one of previous rules can be applied

to an edge, this edge is entirely observed by a sensor

for any optimal solution.

We have found three other rules for determining

other edges indivisible for some optimal solution.

They are based on the idea that for some edge e we

can discard some parts of W(e), having lesser

visibility of the boundary of P than other parts.

Let us recall that the algorithm IEC divides P into a

set of regions whose points share the same visibility

condition of the boundary of P. In particular, each

zone is labeled with: a) the edges seen entirely by

each point of the region; b) the edges seen partially

ICINCO 2005 - ROBOTICS AND AUTOMATION

246

with the number of occlusions. Let E(p) denote the

points of the boundary of P seen by a point p,

excluding points belonging to indivisible edges,

which are fully observed by some other viewpoint.

We say that a region R of W(e

) is the best region of

W(e

) if for any point p∈R and any point q∈(

W(e

)- R) it is E(p)⊇ E(q). It is clear that, if such

region exists, any optimal solution with one

viewpoint in W(e

)-R can be substituted by an

optimal solution with a viewpoint in R. It follows

that all the edges fully observed by R are indivisible.

Then we get the following rule:

Rule3: edges which are completely seen by any

point belonging to the best region of W(e) (if it

exists) are indivisible.

Figure 5: Z

is the best region of W(e

)

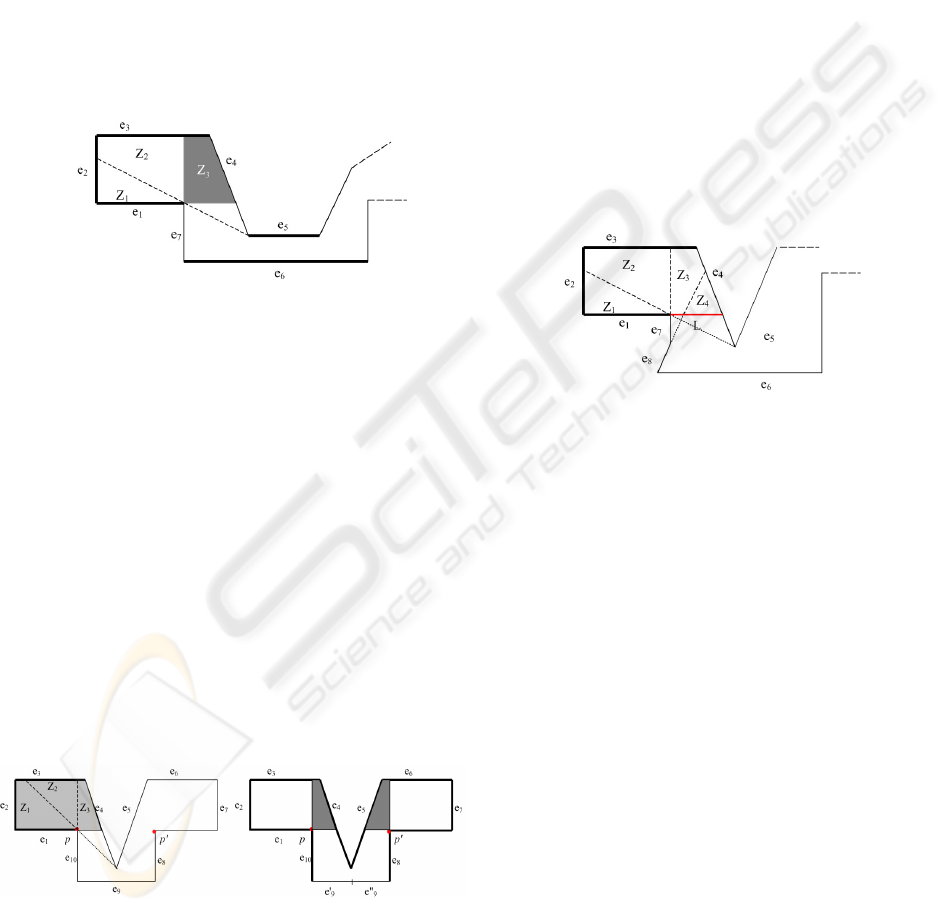
As an example, consider the polygon of Fig. 5. By

applying Rules 1) and 2) we find that edges e

, e

are indivisible. Consider W(e

). Region Z

sees

fully edges e

, e

and partially e

. Region Z

sees

fully edges e

, e

and partially e

, which must

not be considered since it has been already found to

be indivisible. Then Z

is the best region, since any

point in it sees fully edges e

, e

and e

Concluding, we have found that also e

and e

are

indivisible.

The best point of W(e) is defined (if it exist) as the

point p

of W(e) such that E(p

)⊇E(q) (excluding

indivisible edges) for any other point q∈W(e

). If

such a point exists, in any optimal solution a

viewpoint belonging to W(e

) can be substituted by

. Then we get the following rule:

Rule 4: An edge is indivisible if it is observed by the

best point of W(e)

Consider the example of Fig.6.

(a) (b)

Figure 6: Point p is the best point of W(e

) (a). The zones

where two optimal viewpoints can be located (b)

We assume that a viewpoint lying on a vertex of P is

able to see the edges converging at the vertex. This

is justified by the fact that, excluding exceptional

alignment conditions, p can be displaced in a region

nearby without affecting the optimality. Using rules

1 and 2 e

, e

are easily found to be indivisible. It

is clear that p, which sees entirely e

, e

and a part of e

largest or equal to that seen by any

other point is the best point of W(e

). Then also e

and e

are indivisible.

The full algorithm for this polygon works as follows.

LB(P) is 2, as shown in Fig.3. Applying the IC

algorithm we obtain 3 viewpoints. Since this is

different from the lower bound, we apply rules 1, 2

and 4 and find that only e

could be divided. After

splitting in two e

we apply again the IC algorithm,

and find two areas, containing the two best points p

and p’ where the viewpoints can be independently

located (Fig. 6(b)). The cardinality of the solution is

equal to LB(P), and then the solution is optimal.

Figure 7: The line L contains the best boundary points

Let us observe that the definition of best point of a

region W(e

) can be extended, excluding from E(p)

not only other indivisible edges, but also edges or

parts of edges covered by other best points. This is

an effective extension, as it will be shown by the

second example in section 7.

Finally, consider W(e

) in the case shown in Fig.7.

Applying rules (1) and (2) we find that e

, e

are

indivisible. However, we are not able to apply rules

(3) or (4), since in W(e

) there is no best point or

region according to the definition given. This

depends on the fact that there is no point or region

that sees a part of e

larger then any other point.

However, we observe that, for each point p∈W(e

there is a point of the boundary line L that sees the

same set of integer edges, and a larger part of e

This means that any minimal solution with a

viewpoint point inside W(e

) can be transformed in a

minimal solution with a viewpoint lying on L. In

these minimal solution the set of edges entirely

observed is the set entirely observed by any point of

L, in this case e

, e

. Then also e

and e

are

indivisible. We will call a line L the best boundary

lines of W(e) if, for any point q∈W(e) there is a

point p∈L such that E(p)⊇ E(q). We obtain:

A NEW ART GALLERY ALGORITHM FOR SENSOR LOCATION

247

Rule 5: An edge is indivisible if it is entirely

observed by any point of the best boundary line (if it

exists)

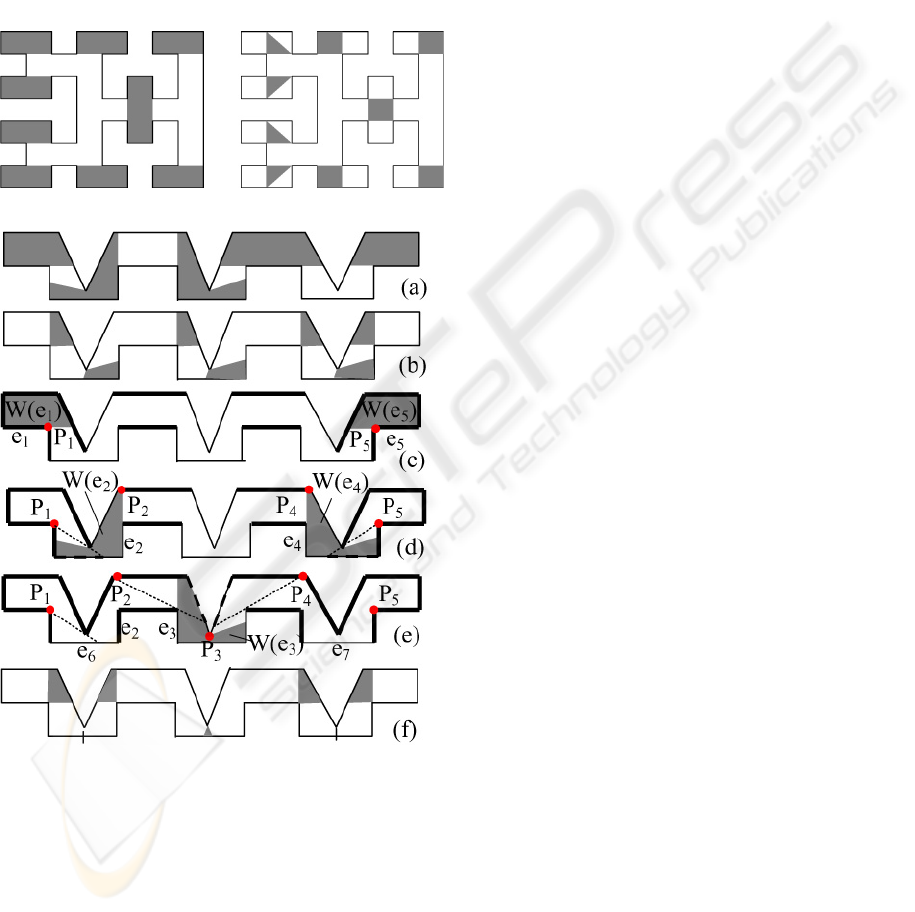
7 TWO EXAMPLES

First, let us apply our algorithm to a polygon taken

from the paper (Gonzales-Banos and Latombe,

2001) of Danner and Kavraki.

Figure 8: LB(P) (left) and an optimal solution (right)

Figure 9: In this case, the algorithm reaches in a few steps

the optimal solution

The cardinality of the maximum set of non-

intersecting weak visibility regions (shown on the

left in Fig.8) is 9. Then LB(P) = 9.

One of the minimum solutions provided by the IC

algorithm is shown in Fig 8 on the right. Since the

number of zones where to independently locate a

minimum set of integer edge guards is 9, this is also

an optimal solution of the unrestricted problem.

In the second example (Fig.9), LB(P) is 5 (Fig.9(a)

and the cardinality of the IC approximation is 7(in

Fig.7(b) one optimal integer cover is shown). Rules

(1), (2) and (4) determine the indivisible edges

shown in Fig.9(c), and two best points of W(e

) and

W(e

). Applying again rule (4) taking into account

the edges and parts of edges (hatched in the figure)

observed by the two best points, two other best

points of W(e

) and W(e

) are found(Fig. 9(d)).

Another application of rule (4) supplies the best

point of W(e

) (Fig.9(e)). Concluding, all edges are

indivisible, excluding e

and e

. Splitting in two

these edges and applying again the IEC algorithm,

the solution shown in Fig.9(f) is found. Five sensors

can be located anywhere in the five regions shown,

and therefore solution is optimal.

8 CONCLUSIONS AND FUTURE

WORK

We have presented a new art gallery sensor location

algorithms. The algorithm starts with an

approximate solution provided by an integer edge

covering algorithm, since in many practical cases

this appears not too far from the optimal solution. A

lower bound for the optimal number of sensor is

computed. If the cardinality of the solution is equal

to the lower bound, the solution is optimal; if not, an

optimal solution can be approached by a local

refinement of the integer edge covering solution. A

set of rules is provided for determining which edges

could be split to approach the optimal solution.

Some examples show how the algorithm works.

Is the algorithm a “good” algorithm for practical

cases, or, in other words, does it supplies in

reasonable time’s solutions close to the optimum?

For assessing its performance, we are currently

implementing the full algorithm and looking for

further rules for finding indivisible edges, as well as

rules for splitting divisible edges. Then we will

apply the algorithm to a number of 2D maps taken

from real environments.

A final remark. Our algorithm can easily take into

account range and incidence constraints. For each

edge e the constraints define a region C(e) of P

where the viewpoint can be located. Applying the

IEC algorithm, we must consider as candidates to

cover an edge e only the regions, or their parts,

belonging to C(e).

ICINCO 2005 - ROBOTICS AND AUTOMATION

248

REFERENCES

A. Bottino, A. Laurentini "Optimal positioning of sensors

in 2D". Proc. 9th Iberoamerican Congress on Pattern

Recognition, Puebla (Mexico), October 26-29, 2004

J.C. Culberson and R.A. Reckhow,” Covering polygons is

hard,” J Algorithms , Vol.17, pp. 2–44,1994

T. Danner and L.E. Kavraki,” Randomized planning for

short inspections paths,” IEEE Int. Conf. On Robotics

and Automation,April 2002, pp. 971-976

S.Eidenbenz, C. Stamm and P. Widmayer,“

Inapproximability results for guarding polygons and

terrains,” Algorithmica, Vol.31, pp.79-113, 2001

H. Gonzales-Banos and J-C. Latombe,” A randomised art

gallery algorithm for sensor placement,” ACM

SCG’01, June3-5,2001

H. Gonzales-Banos and J-C. Latombe.”Planning robot

motion for range-image acquisition and automatic 3D

model construction,” Proc. AAAI Fall Symposyum

Series, 1998

G. D. Kazakakis, and A.A. Argyros, “Fast positioning of

limited visibility guards for inspection of 2D

workspaces,” Proc. 2002 IEEE/RSJ Intl. Conf. On

Intelligent Robots and Systems, pp.2843-2848,

October 2002

A.Laurentini,”Guarding the walls of an art gallery,” The

Visual Computer, vol.15, pp.265-278, 1999

T.S. Newman and A.K. Jain, “A survay of automated

visual inspection,” Comput. Vis. Image Understand. ,

vol.61, no.2, pp.231-262, 1995

J. O’Rourke and K.J. Supowit, “Some NP-hard polygon

decomposition problems,”IEEE Trans IT, Vol.29,

no.2, pp.181-190, March 1983

J. O'Rourke , Art gallery theorems and algorithms, Oxford

University Press, New York,1987

P. Oestergard, “A fast algorithm for the maximum clique

problem,”Discrete Applied Mathematics,Vol.120,

pp.197-207, 2002

J.R.Sack and S.Suri,”An optimal algorithm for detecting

weak visibility of a polygon,” IEEE Trans. on

Computers,Vol.39, pp.1213-1219, 1990

T. Shermer, “Recent results in art galleries,” IEEE Proc.

Vol. 80, pp.1384-1399, 1992

W.R.Scott and G.Roth,”View planning for Automated

Three-Dimensional Object Reconstruction and

Inspection,” ACM Comput. Surveys,Vol.35, No.1,

March 2003, pp.64-96

K.A. Tarabanis, P.K. Allen, and R. Y. Tsai, “ A survey of

sensor planning in computer vision,” ,” IEEE Trans.

Robot. and Automat., vol. 11, no. 1 , pp. 86 –104,

1995

J. Urrutia, "Art Gallery and Illumination Problems"

Handbook on Computational Geometry, Elsevier

Science Publishers, J.R. Sack and J. Urrutia eds. pp.

973-1026, 2000.

D.R. Woods,” An algorithm for finding a maximum clique

in a graph,” Operations Research Letters,

Vol.21, pp.

211-217,1997

A NEW ART GALLERY ALGORITHM FOR SENSOR LOCATION

249