FEASIBLE CONTROL OF COMPLEX SYSTEMS USING

AUTOMATIC LEARNING

Alejandro Agostini and Enric Celaya

Institut de Robòtica i Informática Industrial, C. Llorens i Artigas 4-6, 2

floor, Barcelona, Spain

Keywords: Robot Control, Reinforcement Learning, Categorization.

Abstract: Robotic applications often involve dealing with complex dynamic systems. In these cases coping with

control requirements with conventional techniques is hard to achieve and a big effort has to be done in the

design and tuning of the control system. An alternative to conventional control techniques is the use of

automatic learning systems that could learn control policies automatically, by means of the experience. But

the amount of experience required in complex problems is intractable unless some generalization is

performed. Many learning techniques have been proposed to deal with this challenge but the applicability of

them in a complex control task is still difficult because of their bad learning convergence or insufficient

generalization. In this work a new learning technique, that exploits a kind of generalization called

categorization, is used in a complex control task. The results obtained show that it is possible to learn, in

short time and with good convergence, a control policy that outperforms a classical PID control tuned for

the specific task of controlling a manipulator with high inertia and variable load.

1 INTRODUCTION

Some robotic applications, like the locomotion of a

multi-legged robot, involve dealing with systems

with complex dynamics (Martins-Filho, 2003). In

these cases, the design of the control system and the

tuning of its parameters become a hard task.

A promising alternative is the use of

Reinforcement Learning (RL) systems (Sutton,

1998) able to improve the control policy learning

from experience. But the application of RL in

complex control tasks is often affected by what is

known as the problem of the “curse of

dimensionality” (Sutton, 1998). As a result of this,

learning a satisfactory control policy would require

an unworkable number of experiences and

intolerably long convergence times. Thus, in order to

make the application of RL feasible, generalization

among similar situations is necessary. Function

approximation techniques are usually applied

(Sutton, 1998), (Smart, 2002) but they have bad

convergence properties (Tsitsikilis, 1997), (Thrun,

1993), or are liable to overestimate the utility of the

visited examples (Thrun, 1993).

In (Porta, 2000) a new kind of generalization

called categorization was proposed. We call

categorization the process of finding subsets of

relevant state variables able to characterize certain

situations that require the same control action,

irrespective of the value of those variables that

become irrelevant in such situations.

In (Porta, 2000), a technique to exploit the

categorizability of the environments in a learning

system was proposed with the Categorization and

Learning algorithm (CL algorithm). Some good

preliminary results were obtained in simple

problems with an improved version of the algorithm

(Agostini, 2004a), (Agostini, 2004b). Those

preliminary versions didn’t succeed when applied to

more complex problems. In this work we present a

statistics-based theoretic reformulation of the CL

algorithm that improves several aspects concerning

the categorization process. With this version we

have been able to learn, in short time, a control

policy that outperforms a classical PID control tuned

for the specific task of controlling a manipulator

with high inertia and variable load.

In section 2 the details of the new algorithm are

presented. Section 3 describes the control problem

and the details for the application of the algorithm to

the selected problem. Section 5 gives the results

obtained. Finally, conclusions are in Section 6.

284

Agostini A. and Celaya E. (2005).

FEASIBLE CONTROL OF COMPLEX SYSTEMS USING AUTOMATIC LEARNING.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 284-287

 SciTePress

2 CL ALGORITHM

The CL algorithm attempts to find the relevant

features for every situation to predict the result of

executing an action. We present the fundamental

aspects of the CL algorithm current formulation.

It is assumed that the world is perceived through

n detectors d

i=1...n. Each detector has a set of

different possible values called features d

j=1,..,|d

We say that a feature d

is active when the detector

takes value d

in its perception.

A partial view of order m, m∈{1..n}, is a

subset of m features denoted by v(d

,...,d

) and is a

virtual feature that becomes active when its m

component features are simultaneously active. A

partial rule is a pair formed by a v and an action a,

r(v,a). We say that a partial rule r(v, a) is active each

time that its partial view v is active. We say that

r(v,a) is used each time that it is active and its action

a is executed. In every situation a set of partial rules

is active, and a subset of it, R

, is used. For each

partial rule r three statistic values are stored: q

, an

estimation of the average discounted reward; e

, an

estimation of the variance of q; and n

, the number

of times r has been used.

As in the usual Q-Learning (Watkins, 1992), the

action with highest expected q value must be

determined in every situation the system comes

across. In the case of the CL algorithm, given a

situation there is in general more than one partial

rule active and the problem is to choose the best

prediction of the q value for every possible action.

For each action a, we select the partial rule of R

with lowest dispersion in its observed q values,

which we call the winner partial rule. The dispersion

of a partial rule is determined randomly from the

probability distribution of its unknown standard

deviation σ

(Blom, 1989),

()

≈

(1)

where

1−=

. The value χ

( f ) is randomly

obtained in accordance to a χ

distribution with f

degrees of freedom. This probabilistic dispersion

estimation gives the opportunity to predict the q

value to little tested partial rules with low number of

samples n

, even if they have large e

Note that q

is the estimation of the unknown

mean µ

of the distribution of q. The final estimation

of µ

is determined by random selection using its

probability distribution (Blom, 1989),

eft

)(

+≈

(2)

where t(f) is a random value obtained from the t

distribution with f degrees of freedom.

Finally, the action selected is the one with

highest estimation of µ

. This form of action

selection provides an adaptive form of exploration

that increases the probability of executing

exploratory actions when predictions are less certain,

and favours the testing of those rules that have been

less experienced.

After the execution of the selected action a, a

reward r

is obtained and a new situation R

’ is

reached. The actual q value obtained is computed

using the Bellman’s equation:

{

}

)','(|max.

aRwinnerrqq

∀

(3)

where γ is the discount factor. The obtained q value

is used to update the statistic values in every partial

rule in R

. The q

is updated using the same rule as

Q-Learning for stochastic systems. The e

value is

updated with identical schema. In both cases the

learning coefficient is:

)(

(4)

Some of the situations are observed more

frequently than others. These may cause some

statistic bias in the estimations (Blom, 1989). In

order to prevent these biases we use the

psychological concept of habituation (Grossberg,

1982). Basically, the habituation process consists in

that repetitive stimuli gradually decrease their

influence in the individual behavior. In our case we

consider a partial rule as a stimulus. More habitual

partial rules are updated at a lower rate.

The learning process starts considering partial

rules involving partial views of order 1. To achieve a

good categorization, new partial rules need to be

created. New partial rules are generated by

combining two used ones. Generation is considered

whenever all the partial rules used in the current

situation have been experienced a minimum number

of times in order to have an acceptable confidence in

the estimations. In order to control the proliferation

of partial rules an elimination criterion involving

redundancy is applied. Two partial rules are

redundant if one of them is included in the other and

their q estimations are similar. If two rules are

redundant, the rule with the highest order is

eliminated and the generation of new rules using a

combination of its corresponding detectors is given

less probability to occur.

FEASIBLE CONTROL OF COMPLEX SYSTEMS USING AUTOMATIC LEARNING

285

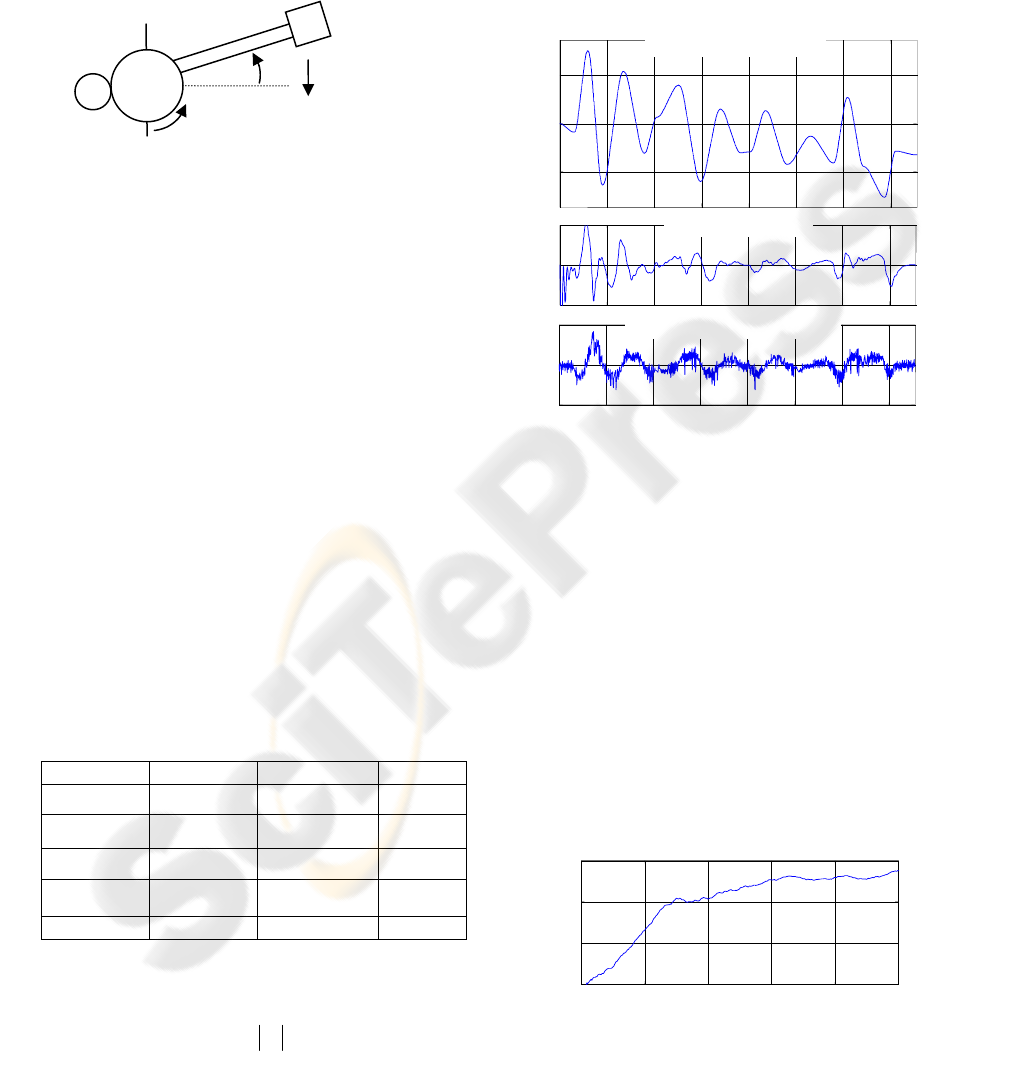
3 APPLICATION EXAMPLE

The algorithm is tested in a control problem

consisting in following randomly generated

trajectories for a rotational manipulator with high

inertia and variable load (figure 1). The actuator (M)

is modeled as a DC motor Maxon 118800 (Maxon).

Figure 1: Manipulator

Model equations are (Craig, 1989):

iKmlGsignnMmlJn

MRR

=+++ )cos()()(

θθθ



(5)



nKVoltRi −=

(6)

where Volt is the input voltage and θ is the angular

position. The simulation is made considering a dt of

1 (ms). The sample frequency is 50 (ms).

In order to evaluate the CL algorithm we

compare the results obtained with a control

performed by a PID system tuned using the second

method of the Ziegler-Nichols rule (Ogata, 2002).

3.1 CL Algorithm Formulation

To make a fair comparison, we use the same input

information as in the PID system: the angular

position error, the angular velocity error, and the

integral of the angular position error

As in Q-learning a discretized representation of

the world is needed (Sutton, 1998) (Table 1).

Position error e

near the 0 value is discretized more

finely and is denoted by e

θ0

Table 1: Features and actions

Detector Range min Range max Features

-π/8 π/8 22

-π/2 π/2 22



-5 5 22

∫

-100π

100π

Volt -48 48 17

Our goal is to follow the reference trajectory as

close as possible. A natural reward function is:

etr

−=)(

(7)

4 RESULTS

To evaluate the control performance of the CL

algorithm 10 different runs of 50000 iterations using

random trajectories were done. The performance

reached after each run is evaluated using a reference

trajectory composed of 20 sigma-shaped randomly

generated subtrajectories of different duration and

angular variation (figure 2).

Figure 2: Instantaneous errors, in larger scale, of the

controls performed by the CL algorithm with minimum

MSE and the PID

The mean squared error (MSE) of the control

performed by the PID system over the reference

trajectory is 3.226E-3 (rad

). The average MSE of

the experiments is 2.704E-3 (rad

). This is a

remarkable result considering that the CL algorithm

uses discretized variables with a reduced number of

segments against the continuous variables used by

the PID system. This fact causes the low amplitude

ripple present in the CL algorithm control.

As shown in figure 3, the CL algorithm presents

a fast learning convergence, obtaining an acceptable

control performance at early stages of the learning

process (in about 15000 iterations, 12 minutes of

real simulation time).

Figure 3: Average reward in the 10 experiments performed

with the CL algorithm

-0.2

0.2

MSE = 3.226E-3 (rad

)

PID Control Erro

(rad)

0 10 20 30 40 50 60 70

-0.2

0.2

time (s)

(rad)

MSE = 1.488E-3 (rad

)

CL Algorithm Control Error

-1

Reference Trajectory

θ (rad)

l=0.5 (m)

m=10 (Kg)

M n=100

0 1 2 3 4 5x10

-1.5

-1

-0.5

Experiments average reward

ewar

iterations

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

286

In order to illustrate how the algorithm

generates relevant partial rules we show in Table 2

the mean number of partial rules generated. To

simplify, we only consider their component

detectors.

Table 2: Mean number of partial rules

Detectors Number of rules

Order 1 1469

},{



2085

},{



388

},{

∫

θθ

269

},{

∫

θθ

444

},{

∫



},,{

∫

eee



2485

},,{

∫

eee



232

Total 7457

The number of rules generated is very low

compared with the total number of possible

situations, about 362E3, showing the high

generalization reached. The CL algorithm is capable

to learn that the position error is very relevant for the

control task generating rules contain this feature.

The CL algorithm was capable to generate partial

rules containing the velocity error in regions of the

state space near the reference trajectory in which this

detector becomes relevant.

5 CONCLUSIONS

In this work we presented a learning approach that

uses a new kind of generalization, which we called

categorization. The application of this learning

system compares well with traditional control

techniques, and even outperforms them. The CL

algorithm can reach a high generalization with fast

learning convergence. This illustrates the viability of

its application for complex control.

The next step will be the application of

continuous domain methods in the CL algorithm

expecting to overcome the existing problems of

automatic learning in complex control tasks.

ACKNOWLEDGEMENTS

This work has been partially supported by the

Ministerio de Ciencia y Tecnología and FEDER,

under the project DPI2003-05193-C02-01 of the

Plan Nacional de I+D+I.

REFERENCES

Agostini, A., Celaya, E., 2004a. Learning in Complex

Environments with Feature-Based Categorization. In

Proc. of 8th Conference on Intelligent Autonomous

Systems. Amsterdam, The Netherland, pp. 446-455.

Agostini, A., Celaya, E., 2004b. Trajectory Tracking

Control of a Rotational Joint using Feature Based

Categorization Learning. In Proc. of IEEE/RSJ

International Conference on Intelligent Robots and

Systems. Sendai, Japan, pp. 3489-3494.

Blom, G., 1989. Probability and Statistics: Theory and

Applications. The book. Springer-Verlag.

Craig, J., 1989. Introduction to Robotics. The book, 2nd

Ed. Addison-Wesley Publishing Company.

Grossberg, S., 1982. A Psychophysiological Theory of

Reinforcement, Drive, Motivation and Attention.

Journal of Theoretical Neurobiology, 1, 286 369.

Martins-Filho, L., Silvino, j., Presende, P., Assunçao, T.,

2003. Control of robotic leg joints – comparing PD

and sliding mode approaches. In Proc. of the Sixth

International Conference on Climbing and Walking

Robots (CLAWAR2003). Catania, Italy, pp.147-153.

Maxon Motor (n. d.). High Precision Drives and Systems.

Maxon Interelectric AG, Switzerland. From Maxon

Motor Web site http://www.maxonmotor.com.

Ogata, K., 2002. Modern Control Engineering. The book.

ed., Prentice Hall, New Jersey, United State.

Porta, J. M. and Celaya, E., 2000. Learning in

Categorizable Environments. In Proc. of the Sixth

International Conference on the Simulation of

Adaptive Behavior (SAB2000). Paris, pp.343-352.

Smart, W. and Kaelbling, L., 2000. Practical

reinforcement learning in continuous spaces. In Proc.

of the Seventeenth International Conference on

Machine Learning (ICML).

Sutton, R. and Barto, 1998. Reinforcement Learning. An

Introduction. The book. MIT Press.

Thrun, S. and Schwartz, A., 1993. Issues in Using

Function Approximation for Reinforcement Learning.

In Proc. of the Connectionist Models Summer School.

Hillsdale, NJ, pp. 255-263.

Tsitsikilis, J. and Van Roy, B., 1997. An Analysis of

Temporal Difference Learning with Function

Approximation. IEEE Transactions on Automatic

Control, 42(5):674--690.

Watkins, C., Dayan, P., 1992. Q-Learning. Machine

Learning, 8:279-292.

FEASIBLE CONTROL OF COMPLEX SYSTEMS USING AUTOMATIC LEARNING

287