VISUALLY SERVOING A GOUGH-STEWART PARALLEL ROBOT

ALLOWS FOR REDUCED AND LINEAR KINEMATIC

CALIBRATION

Nicolas Andreff and Philippe Martinet

LAboratoire des Sciences et Mat

eriaux pour l’Electronique et d’Automatique (LASMEA)

UMR 6602 CNRS-Universit

e Blaise Pascal

24 avenue des Landais, 63177 Aubire Cedex, France

Keywords:

parallel robot, visual servoing, redundant metrology, kinematic calibration.

Abstract:

This paper focuses on the beneﬁts of using computer vision to control a Gough-Stewart parallel robot. Namely,

it is recalled that observing the legs of such a mechanism with a calibrated camera, thus following the redun-

dant metrology paradigm, simpliﬁes the control law. Then, we prove in this paper that such a control law

depends on a reduced set of kinematic parameters (only those attached to the geometry of the robot base) and

that these parameters can be obtained by solving a linear system. Moreover, we show that the camera can

be calibrated without much experimental effort, simply using images of the robot itself. All this means that

setting up the control system consists only in placing the camera in front of the robot.

1 INTRODUCTION

Parallel mechanism are such that there exist several

kinematic chains (or legs) between their base and their

end-effector. Therefore, they may exhibit a better re-

peatability (Merlet, 2000) than serial mechanisms but

not a better accuracy (Wang and Masory, 1993), be-

cause of the large number of links and passive joints.

There can be two ways to compensate for the low ac-

curacy. The ﬁrst way is to perform a kinematic cali-

bration of the mechanism and the second one is to use

a control law which is robust to calibration errors.

There exists a large amount of work on the control

of parallel mechanisms

. In the focus of attention,

Cartesian control is naturally achieved through the

use of the inverse Jacobian which transforms Carte-

sian velocities into joint velocities. It is noticeable

that the inverse Jacobian of parallel mechanisms does

not only depend on the joint conﬁguration (as for ser-

ial mechanisms) but also on the end-effector pose.

Consequently, one needs to be able to estimate or

measure the latter. As far as we know, all the effort

has been put on the estimation of the end-effector

pose through the forward kinematic model and the

joint measurements. However, this yields much trou-

ble, related to the fact that in general, there is no

See http://www-sop.inria.fr/coprin/equipe/merlet for a

long list of references.

closed-form solution to the forward kinematic prob-

lem. Hence, one numerically inverts the inverse kine-

matic model, which is analytically deﬁned for most of

the parallel mechanisms. However, it is known (Mer-

let, 1990; Husty, 1996) that this numerical inver-

sion requires high order polynomial root determina-

tion, with several possible solutions (up to 40 real

solutions for a Gough-Stewart platform (Dietmaier,

1998)). Much of the work is thus devoted to solv-

ing this problem accurately and in real-time (see for

instance (Zhao and Peng, 2000)), or to designing par-

allel mechanisms with analytical forward kinematic

model (Kim and Tsai, 2002; Gogu, 2004). One of

the promising paths lies in the use of the so-called

metrological redundancy (Baron and Angeles, 1998),

which simpliﬁes the kinematic models by introducing

additional sensors into the mechanism and thus yields

easier control (Marquet, 2002).

Visual servoing (Espiau et al., 1992; Christensen

and Corke, 2003) is known to robustify the Carte-

sian control of serial and mobile robots, with tech-

niques ranging from position-based visual servoing

(PBVS) (Martinet et al., 1996) (when the pose mea-

surement is explicit) to image-based visual servoing

(IBVS) (Espiau et al., 1992) (when it is made implicit

by using only image measurements). Visual servo-

ing techniques are very effective since they close the

control loop on the vision sensor, which gives a di-

rect view of the Cartesian space. This yields a high

119

Andreff N. and Martinet P. (2005).

VISUALLY SERVOING A GOUGH-STEWART PARALLEL ROBOT ALLOWS FOR REDUCED AND LINEAR KINEMATIC CALIBRATION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 119-124

DOI: 10.5220/0001174301190124

 SciTePress

robustness to robot calibration errors. Indeed, these

errors only appear in a Jacobian matrix but not in the

regulated error.

Essentially, visual servoing techniques generate a

Cartesian desired velocity which is converted into

joint velocities by the robot inverse Jacobian. Hence,

one can translate such techniques to parallel mecha-

nisms as in (Koreichi et al., 1998; Kallio et al., 2000)

by observation of the robot end-effector and the use of

standard kinematic models. It is rather easier than in

the serial case, since the inverse Jacobian of a parallel

mechanism has a straightforward expression. More-

over, for parallel mechanisms, since the joint veloc-

ities are ﬁltered through the inverse Jacobian, they

are admissible, in the sense that they do not gener-

ate internal forces. More precisely, this is only true

in the theoretical case. However, if the estimated in-

verse Jacobian used for control is close enough to the

actual one, the joint velocities will be closely admis-

sible, in the sense that they do not generate high in-

ternal forces.The only difﬁculty would come from the

dependency of the inverse Jacobian to the Cartesian

pose, which would need be estimated, but, as stated

above, vision can also do that (DeMenthon and Davis,

1992; Lavest et al., 1998) ! Notice that this point

pleads for PBVS rather than IBVS of parallel mecha-

nisms.

Nevertheless, the direct application of visual ser-

voing techniques assumes implicitly that the robot in-

verse Jacobian is given and that it is calibrated. There-

fore, modeling, identiﬁcation and control have small

interaction with each other. Indeed, the model is usu-

ally deﬁned for control using proprioceptive sensing

only and does not foresee the use of vision for con-

trol, then identiﬁcation and control are deﬁned with

the constraints imposed by the model. This is useful

for modularity but this might not be efﬁcient in terms

of accuracy as well as of experimental set-up time.

On the opposite, instead of having identiﬁcation

and control being driven by the initial modeling stage,

one could have a model taking into account the use of

vision for control and hence for identiﬁcation. To do

so, a new way to use vision, which gathers the ad-

vantages of redundant metrology and of visual servo-

ing and avoids most of their drawbacks was presented

in (Andreff et al., 2005).

Indeed, adding redundant sensors is not always

technically feasible (think of a spherical joint) and al-

ways requires either that the sensors are foreseen at

design stage or that the mechanism is physically mod-

iﬁed to install them after its building. Anyhow, there

are then additional calibration parameters in the kine-

matic model and one needs to estimate them in order

to convert redundant joint readings into a unit vector

expressed in the appropriate reference frame. More-

over, observing the end-effector of a parallel mecha-

nism by vision may be incompatible with its applica-

Figure 1: A Gough-Stewart platform observed by a camera

with short focal length.

tion. For instance, it is not wise to imagine observing

the end-effector of a machining tool. On the opposite,

it should not be a problem to observe the legs of the

mechanism, even in such extreme cases. Thereby one

would turn vision from an exteroceptive sensor to a

somewhat more proprioceptive sensor. This brings us

back to the redundant metrology paradigm.

With such an approach, the control is made easier

by measuring a major part of the robot inverse Jaco-

bian, reducing the number of kinematic parameters to

be identiﬁed. We will show in this paper that these

remaining parameters can be estimated by solving a

linear system.

The remainder of the paper is the following. Sec-

tion 2 recalls the vision-based control of the Gough-

Stewart robot. Section 3 discusses the actual choice of

vision for such a control. Section 4 presents the cali-

bration procedure for the whole system. Finally, sim-

ulation results and conclusion are given respectively

in section 5 and section 6.

2 VISION-BASED KINEMATICS

Consider the hexapod in Figure 1. It has 6 legs of

varying length q

, i ∈ 1..6, attached to the base by

spherical joints located in points A

and to the mov-

ing platform (end-effector) by spherical joints located

in points B

. The inverse kinematic model of such an

hexapod is given by

∀i ∈ 1..6, q

−−−→

(1)

expressing that q

is the length of vector

−−−→

. This

model can be expressed in any Euclidean reference

frame. Hence, it can be expressed in the base frame

, in the end-effector frame R

or in the camera

frame R

. Hereafter, the camera reference frame will

be used and denoted by a left upper-script.

ICINCO 2005 - ROBOTICS AND AUTOMATION

120

According to (Andreff et al., 2005) and assuming

a calibrated camera, one can express the vision-based

kinematics of the hexapod expressed in the camera

frame:

−

(2)

q =

inv

(3)

with

inv

= −





(

)

(

)





(4)

where

is the Cartesian velocity of the camera

frame, considered as attached to the base frame and

moving with respect to a ﬁxed end-effector, expressed

in itself and

, i = 1..6 are the unit vectors giving

the pointing direction of each leg in the camera frame.

Then, one can derive a control law of the form:

(5)

E = (e

, ..., e

)

(6)

) =



−



(7)

= P(

) [

−[

+ q

]

] (8)

[

]

(9)

= (N

, ..., N

)

(10)

q = −λ

inv

diag(q)E (11)

where the hat means that only an estimate can be used

and []

denotes the antisymmetric matrix associated

to the cross-product.

3 DISCUSSION

Here, the above control is discussed, with explicit re-

gard to the sensing problem. Indeed, it does not ab-

solutely imply that computer vision should be used

for that.

3.1 Why vision should be used

rather than joint sensors

There are three manners to measure or estimate the

’s. The ﬁrst one, which we discard of course im-

mediately, is to estimate the end-effector pose with

respect to the base by numerical inversion of the in-

verse kinematic model and then use (2) to obtain u

The second manner is to place joint sensors in the

’s, so that they would deliver the pointing direc-

tion of the leg. This manner is valid since the u

’s

would be measured and not estimated through a del-

icate numerical procedure as above. Nevertheless, it

is, in our opinion, still not the correct manner. Indeed,

Figure 2: Projection of a cylinder in the image.

a joint sensor delivers a value expressed in its own ref-

erence frame. To convert this value in the base frame

would require either an extremely accurate assembly

procedure or the identiﬁcation of the relative orien-

tation of each joint sensor frame with respect to the

base frame. Moreover, additional joint offsets would

need be identiﬁed.

Since the leading vector of a leg is essentially a

Cartesian feature, we chose to estimate it by vision.

Indeed, vision is an adequate tool for Cartesian sens-

ing, and, following (Renaud et al., 2004), if vision is

also chosen for calibration, this does not add extra cal-

ibration parameter. It will even be shown in Section 4

that using vision reduces the parameter set needed for

control.

3.2 Cylindrical leg observation

Now the problem is to recover

from the leg ob-

servation. It may be somehow tedious, although

certainly feasible, in the case of an arbitrary shape.

Hopefully, for mechanical reasons such as rigidity,

most of the parallel mechanisms are not only designed

with slim and rectilinear legs, but, even better, with

cylindrical shapes.

Except in the degenerated case where the projec-

tion center lies on the cylinder axis, the visual edge of

a cylinder is a straight line (Figure 2). Consequently,

it can be represented by its Binormalized Pl

ucker co-

ordinates (Andreff et al., 2002) in the camera frame.

Let us note

and

the image projections of

the two edges of a cylinder, that can be tracked us-

ing the results in (Marchand and Chaumette, 2005).

These two vectors are oriented so that they point from

the cylinder revolution axis outwards. Then, their ex-

pression is related to the Binormalized Pl

ucker Coor-

dinates (

h) of the cylinder axis (see Figure 3)

VISUALLY SERVOING A GOUGH-STEWART PARALLEL ROBOT ALLOWS FOR REDUCED AND LINEAR

KINEMATIC CALIBRATION

121

image plane

Figure 3: Construction of the visual edges of a cylinder: the

cylinder is viewed from the top.

= −cos θ

− sin θ

u ×

h (12)

= + cos θ

− sin θ

u ×

h (13)

where cos θ =

√

− R

h and sin θ = R/

h = k

A ×

h = (

A ×

u)/

h and R is the

cylinder radius.

Then, it is easy to show that the leading vector

of the cylinder axis, expressed in the camera frame,

writes

(14)

Notice that the geometric interpretation of this result

is that

is, up to a scale factor, the vanishing point

of the two image edges, i.e. their intersection point in

the image.

4 VISION-BASED CALIBRATION

As stated earlier in this paper, the vision-based con-

trol (2)-(11) relies on the use of a calibrated camera

and on some kinematic parameters.

The classical approach for calibrating a camera is

to use a calibration grid made of points (Brown, 1971;

Tsai, 1986; Faugeras and Toscani, 1987; Lavest et al.,

1998). However, in the present case, it is more per-

tinent to use the method proposed in (Devernay and

Faugeras, 2001). Indeed, this method is based on the

observation of a set of lines, without any assumption

on their 3D structure. As can be seen in Figure 1,

there are plenty of lines in the images observed by

a camera placed in front of a Gough-Stewart parallel

robot. Hence, the camera can be calibrated on-line

without any experimental burden.

Now, the only kinematic parameters the control law

depends on are the attachment points of the legs onto

the base expressed in the camera frame (

) and on

the joint offsets. The latter appear in two places : un-

der the form

+ q

in (8) and as a gain in (9).

Considering the order of magnitude of

and q

one can neglect small errors on the joint offsets in (8).

Moreover, since the joints are prismatic it is easy to

measure their offsets manually with a millimetric ac-

curacy. This is also highly sufﬁcient to ensure that the

gain in (9) is accurate enough. This means that, as far

as control is concerned, one only needs to identify the

attachment points onto the base, but there is no need

for identifying the other usual kinematic parameters:

attachment points onto the mobile platform and joint

offsets.

In (Renaud et al., 2004), a calibration procedure

was proposed, using legs observation, where, in a

ﬁrst step, the points A

were estimated in the cam-

era frame, then in a second step were expressed in the

base frame, and ﬁnally the others kinematic parame-

ters where deduced. Essentially, only the ﬁrst step of

this procedure is needed.

This step is reformulated here in a more elegant

way, using the Binormalized Pl

ucker Coordinates of

the cylinder edges (12), and minimizing an image-

based criterion.

Assuming that the attachment point A

is lying on

the revolution axis of the leg and referring again to

Figure 3, one obtains, for any leg i and robot conﬁgu-

ration j,

i,j

= −R (15)

i,j

= −R (16)

Stacking such relations for n

robot conﬁgurations

yields the following linear system







i,1

i,n













−R







(17)

which has a unique least-square solution if there are

at least two conﬁgurations with different leg orienta-

tions.

The calibration procedure is hence reduced to a

strict minimum. To improve its numerical efﬁciency,

one should only take care to use robot conﬁgurations

with the larger angles between each leg orientation.

However, since the

only appear in the interaction

matrix, they do not require a very accurate estimation.

5 RESULTS

A commercial DeltaLab hexapod was simulated,

such that

= R



cos(k

+α)

sin(k

+α)



2k+1

ICINCO 2005 - ROBOTICS AND AUTOMATION

122

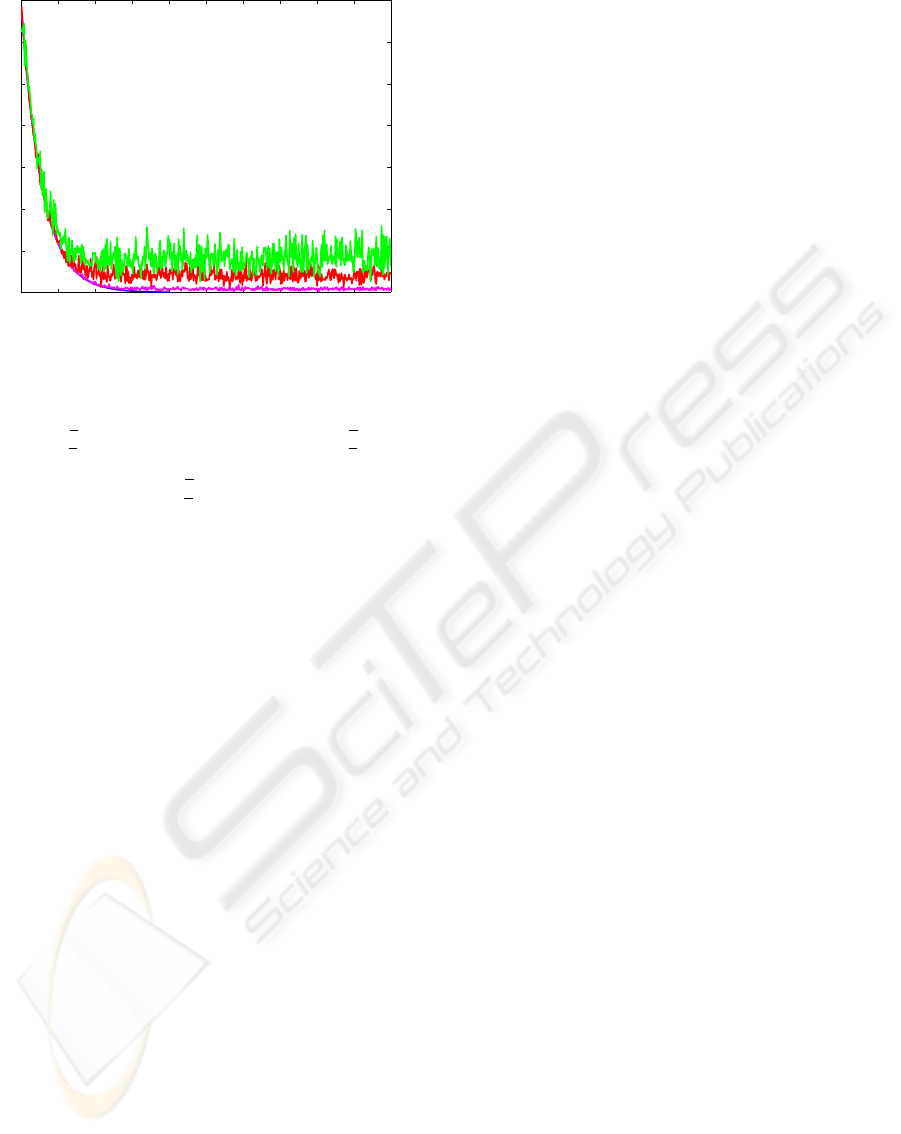
0 50 100 150 200 250 300 350 400 450 500

0.05

0.1

0.15

0.2

0.25

0.3

0.35

Figure 4: Robustness to noise : sum of squares of the errors

E with a noise amplitude of 0 deg, 0.01 deg, 0.05 deg

and 0.1 deg.



cos(k

−α)

sin(k

−α)



= R



cos(k

+β)

sin(k

+β)



2k+1

= R



cos(k

−β)

sin(k

−β)



, k ∈ {0, 1, 2} with

= 270mm, α = 4.25

◦

, R

= 195mm, β =

5.885

◦

and the legs range are [345mm, 485mm].

5.1 Image noise

It is not immediate to model realistically the effect of

image noise on detecting the visual edges of a cylin-

der. One can imagine to use the (ρ, θ) representation

of an image line and to add noise to these two compo-

nents. However, it is not certain that the two noise

components are uncorrelated. Alternately, one can

also determine the virtual intersections of the visual

edge with the image border and to add noise to these

intersections (Bartoli and Sturm, 2004).

An alternative model is presented here, which takes

advantage of the fact that an image line is essentially

a unit vector. Thus, image noise will necessary result

into a rotation of this unit vector. Consequently, one

needs to deﬁne a random rotation matrix, that is to

say a rotation axis and a positive rotation angle. Pre-

liminary tests showed that simply taking this axis as

a uniformly distributed unit vector and this angle as a

uniformly distributed positive scalar gives a realistic

behavior.

This noise model has for advantages that it is easy

to implement, it does not depend on the simulated im-

age size, and is parametered by a single scalar (i.e. the

maximal amplitude of the rotation angle).

To give an idea of how to choose this maximal am-

plitude, an error of about ± 1 pixel on the extremities

of a 300 pixel-long line segment yields a rotation an-

gle of approximately 0.05 degree.

5.2 Calibration validation

In order to quantify the calibration procedure, the sim-

ulated robot was calibrated by moving it into its 64 ex-

tremal conﬁgurations (i.e. each leg joint is extended

to its lower limit then to its upper limit). In each con-

ﬁguration, the visual edges of each leg were generated

from the inverse kinematic model and added noise as

described above, with a maximal amplitude of 0.05

degree. This calibration procedure was repeated 100

times. As a result, the median error on each attach-

ment point is less than 1 mm.

5.3 Realistic simulation

Now, a more realistic simulation is presented where

the calibration is ﬁrst performed using the 64 extremal

conﬁgurations, then control is launched using the cal-

ibrated values. Noise is added as above during image

detection, with amplitudes of 0.01, 0.05 and 0.1 de-

gree.

It is noticeable that the calibration errors (in terms

of maximal error on each of the component of each

attachment point) is respectively of 0.5, 1.4 and 10

mm.

Graphically (Figure 4), the sum of the errors on

each leg E

E still decreases. Additionally, the me-

dian positioning error of the convergence tails in Fig-

ure 4 are respectively 0.1, 0.6 and 1.1 mm while the

maximal error are 0.6, 1.9 and 3 mm.

Hence, the overall calibration-control process

seems rather robust to image measurement errors.

6 CONCLUSION

A fundamentally novel approach was proposed

in (Andreff et al., 2005) for controlling a parallel

mechanism using vision as a redundant sensor, adding

a proprioceptive nature to the usual exteroceptive na-

ture of vision. The present paper shows that such a

method not only simpliﬁes the control law, but also

reduces the experimental effort.

Indeed, on the opposite to standard Cartesian con-

trol, no numerical inversion of the inverse kinematic

model is required. Moreover, the kinematic parameter

set which is effectively used during vision-based con-

trol is smaller than the one used for Cartesian control.

Additionally, the kinematic calibration is turned lin-

ear with the vision-based approach.

From a practical point of view, setting-up such a

control is made easier than any other ones. Indeed,

on the opposite to most of the visual servoing ap-

proaches, there is no need to mount a visual target

onto the robot end-effector, since the visual targets are

the very robot legs. As far as calibration is concerned

VISUALLY SERVOING A GOUGH-STEWART PARALLEL ROBOT ALLOWS FOR REDUCED AND LINEAR

KINEMATIC CALIBRATION

123

again, the calibration of the camera can be done with

the same observation, as well as the kinematic cali-

bration, which does not require any more any speciﬁc

set-up.

Of course, all these beneﬁts can only be obtained

to a higher cost in software integration and devel-

opment, which is not completely terminated at the

present time, preventing us from showing experimen-

tal results.

ACKNOWLEDGMENT

This study was jointly funded by CPER Auvergne

2003-2005 program and by the CNRS-ROBEA pro-

gram through the MP2 project.

REFERENCES

Andreff, N., Espiau, B., and Horaud, R. (2002). Visual ser-

voing from lines. Int. Journal of Robotics Research,

21(8):679–700.

Andreff, N., Marchadier, A., and Martinet, P. (2005).

Vision-based control of a Gough-Stewart parallel

mechanism using legs observation. In Proc. Int. Conf.

Robotics and Automation (ICRA’05), pages 2546–

2551, Barcelona, Spain.

Baron, L. and Angeles, J. (1998). The on-line direct kine-

matics of parallel manipulators under joint-sensor re-

dundancy. In Advances in Robot Kinematics, pages

126–137.

Bartoli, A. and Sturm, P. (2004). The 3d line motion matrix

and alignement of line reconstructions. Int. Journal of

Computer Vision, 57(3):159–178.

Brown, D. (1971). Close-range camera calibration. Pho-

togrammetric Engineering, 8(37):855–866.

Christensen, H. and Corke, P., editors (2003). Int. Journal of

Robotics Research – Special Issue on Visual Servoing,

volume 22.

DeMenthon, D. and Davis, L. (1992). Model-based object

pose in 25 lines of code. Lecture Notes in Computer

Science, pages 335–343.

Devernay, F. and Faugeras, O. (2001). Straight lines have to

be straight. Machine Vision and Applications, 13:14–

24.

Dietmaier, P. (1998). The Stewart-Gough platform of gen-

eral geometry can have 40 real postures. In Lenar

J. and Husty, M. L., editors, Advances in Robot Kine-

matics: Analysis and Control, pages 1–10. Kluwer.

Espiau, B., Chaumette, F., and Rives, P. (1992). A New Ap-

proach To Visual Servoing in Robotics. IEEE Trans.

on Robotics and Automation, 8(3).

Faugeras, O. and Toscani, G. (Tokyo, japan, 1987). Camera

calibration for 3d computer vision. In International

Conference on Computer Vision and Pattern Recogni-

tion (CVPR).

Gogu, G. (2004). Fully-isotropic T3R1-type parallel ma-

nipulator. In Lenar

c, J. and Galletti, C., editors, On

Advances in Robot Kinematics, volume Kluwer Aca-

demic Publishers, pages 265–272.

Husty, M. (1996). An algorithm for solving the direct kine-

matics of general Gough-Stewart platforms. Mech.

Mach. Theory, 31(4):365–380.

Kallio, P., Zhou, Q., and Koivo, H. N. (2000). Three-

dimensional position control of a parallel microma-

nipulator using visual servoing. In Nelson, B. J.

and Breguet, J.-M., editors, Microrobotics and Mi-

croassembly II, Proceedings of SPIE, volume 4194,

pages 103–111.

Kim, H. and Tsai, L.-W. (2002). Evaluation of a Cartesian

parallel manipulator. In Lenar

c, J. and Thomas, F.,

editors, Advances in Robot Kinematics: Theory and

Applications. Kluwer Academic Publishers.

Koreichi, M., Babaci, S., Chaumette, F., Fried, G., and

Pontnau, J. (1998). Visual servo control of a paral-

lel manipulator for assembly tasks. In 6th Int. Sympo-

sium on Intelligent Robotic Systems, SIRS’98, pages

109–116, Edimburg, Scotland.

Lavest, J., Viala, M., and Dhome, M. (1998). Do we really

need an accurate calibration pattern to achieve a reli-

able camera calibration. In Proceedings of ECCV98,

pages 158–174, Freiburg, Germany.

Marchand, E. and Chaumette, F. (2005). Feature track-

ing for visual servoing purposes. Robotics and Au-

tonomous Systems.

Marquet, F. (2002). Contribution

a l’

etude de l’apport de

la redondance en robotique parall

ele. PhD thesis,

LIRMM - Univ. Montpellier II.

Martinet, P., Gallice, J., and Khadraoui, D. (1996). Vision

based control law using 3d visual features. In Proc.

World Automation Congress, WAC’96, Robotics and

Manufacturing Systems, volume 3, pages 497–502,

Montpellier, France.

Merlet, J.-P. (1990). An algorithm for the forward kinemat-

ics of general 6 d.o.f. parallel manipulators. Technical

Report 1331, INRIA.

Merlet, J.-P. (2000). Parallel robots. Kluwer Academic

Publishers.

Renaud, P., Andreff, N., Gogu, G., and Martinet, P. (2004).

On vision-based kinematic calibration of a Stewart-

Gough platform. In 11th World Congress in Mech-

anism and Machine Science (IFToMM2003), pages

1906–1911, Tianjin, China.

Tsai, R. (Miami, UsA, 1986). An efﬁcient and accurate

calibration technique for 3d machine vision. In Inter-

national Conference on Computer Vision and Pattern

Recognition (CVPR), pages pp 364–374.

Wang, J. and Masory, O. (1993). On the accuracy of a Stew-

art platform - Part I : The effect of manufacturing tol-

erances. In Proc. ICRA93, pages 114–120.

Zhao, X. and Peng, S. (2000). Direct displacement analysis

of parallel manipulators. Journal of Robotics Systems,

17(6):341–345.

ICINCO 2005 - ROBOTICS AND AUTOMATION

124