SUS A NEW GENERATION THINKING ROBOTS
The Visual Intelligence Tests
Zbigniew Les and Magdalena Les
The Queen Jadwiga Research Institute of Understanding
P.O. Box 654, Toorak, Victoria 3142, Australia
Keywords: Shape understanding, intelligence test, visual concept, visual reasoning.
Abstract: In this paper understanding abilities of the shape understanding system (SUS) are tested based on the
methods used in the intelligence tests. These tests are formulated as tasks given to the system and
performance is compared with the human performance of these tasks. The tests were based on the
progressive matrices test which requires the good visual problem solving abilities of the human subject.
SUS solves these tests by transforming the visual form into the string form. The proposed string form makes
it possible to perform complex visual reasoning. The experiment proved that the proposed method, which is
part of the SUS visual understanding abilities, can solve the test that is very difficult for human subject
.
1 INTRODUCTION
Understanding is based on abilities called
intelligence such as a verbal communication, spatial
orientation, memorizing, and reasoning. Intelligence
tests are series of tasks designed to measure the
capacity to make abstractions, to learn and to deal
with novel situations. Intelligence tests that include
tasks that deal with visual forms (shapes) are called
the visual tests. They are divided into several
groups: the visual discrimination tests, the visual
memory tests, the visual-spatial relationship tests,
the visual form constancy tests, the visual sequential
memory tests, the visual figure ground tests or the
visual closure tests (Colaruso 2003), (Gardener
1996).
The system that has abilities to understand the visual
information needs to be able to solve tasks that are
presented in the form of visual intelligence tests.
Intelligence tests include tasks that deal with visual
forms (shapes). In the present research, that is part of
the shape understanding method, the shape is
considered as a meaningful unit called the phantom.
Existing methods of shape analysis are mostly
concerned with shape recognition (Bhanu 1984), (Lu
1993), (He 1991), (Kartikeayan 1989), (Pal 1993).
Visual systems applying shape as their knowledge
are called the model-based object recognition
systems and have been used extensively by vision
researchers (Pope 1994).
2 UNDERSTANDING OF THE
VISUAL OBJECT
Shape understanding method (Les 2002), (Les 2003)
is a multidisciplinary research area that is focused on
understanding of the visual objects. This method is
based on the concept of possible classes of shape.
For example, the convex polygon class consists of
the elements that are called convex polygons and is
denoted as
n
L , where n refers to the number of
sides. The symbol
n
L denotes the symbolic name of
the class. The detailed description of the classes such
as the thin class, the convex polygon class, the curve
polygon class, the cyclic class and the complex class
are given in references (Les 2002), (Les 2003), (Les
2005), and (Les 2005). In this paper the short
description of the notation of the symbolic names is
given. The description is limited to the class from
which exemplars are part of the visual intelligence
test. In Fig.1 are presented exemplars from the
convex polygon class: the triangle class
3
L , the
quadrilateral class
4
L , the convex curve polygon
class
M
, the convex curve class
K
, the concave
polygon classes
)(
3
5
LQ
L
and )2(
32
5
LQ
L
(Fig. e,f),
the concave curve class
)(
11
1
MQ
M
, the thin class
415
Les Z. and Les M. (2005).
SUS A NEW GENERATION THINKING ROBOTS - The Visual Intelligence Tests.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 415-424
DOI: 10.5220/0001174404150424
Copyright
c
 SciTePress

]),,([
3
3
mml
E
L
Θ
, the acyclic class )3(
33
4
LA
L
, the
drawing class
)}3({
33
4
LAG
L
, and the complex thin
class
),,,,(,(
1
ssbssKC Θ ,
)))(),(,),(),((,(
1
hclsblshcKC Θ
.
Figure 1: Exemplars from the convex polygon class
3 THE STRING FORM - THE
TYPE OF THE CLASS
Archetypes of the shape class are described in the
form of the symbolic names. For the purpose of the
visual reasoning the symbolic name is transformed
into the string form. The string consists of
combination of the selected letters, numbers and the
symbol “|”. The string has a following form:
B1|…|Bi|...|Bn|, where Bi denotes the symbolic
names of the class.
There is a conversion from the notation of the
symbolic name into the string notation. For example,
the convex class
3
L is expressed as L3 in the string
form.
The string notation is used to introduce the type of
the class. The string without symbol “|” denotes the
type P of the class. It represents exemplars of the
convex classes. For example, exemplars of convex
classes given in Fig.2 (L3A, L4R, M1L3A, M1L4R,
M2L4R) are all of type P.
Figure 2: Exemplars of the class of type P
Type S represents cyclic and concave classes. The
type S is given in the form
Sn|A|1X|…|iX|…|nX|. The type Sq (the concave
type) is given in the form Qn|G|1R|…|iR|…|nR|,
whereas the type Sa (the cyclic type) is given as
An|C|1W|…|iW|…|nW|. Examples of the exemplars
type Sn|A|1X|…|iX|…|nX| are given in Fig.13, 14,
and 15. The type S1|A|1_S1|1_A|1_X| and the type
S1|A|1_S1|1_A|2_S1|2_A|2_X| represent the
exemplars o of the convex or cyclic classes on the
first and the second level of iteration. The concave
class
)4(
34
4
LQ
L
is expressed as Q4|L4|L3|L3|L3| in
the string form.
4 VISUAL TESTS IN SUS
In SUS visual test is given as a series of eight
objects
8,..1, =iv
i
. These objects are denoted using
matrix notation
3,..1,,
,
=jiv
ji
to represent the
pattern in the test. The five objects that are given as
an answer are denoted as
5,..1, =ko
k
(see Fig 3).
Figure 3: Examples of tests and answers
The task is formulated as ‘find the object
5,..1, =ko
k
that fills the missing entry in the matrix
3,..1,,
,
=jiv
ji
:
σ >
k
ji
kk
okjiforvoo ⇒==⊗∃ ]5,...,13,..1,,:[
,
. The
symbol ‘
⊗
’ denotes the matching between the
possible solution
ji
v
,
and the answer object
.
k
o
The visual test is given as a pattern that consists of
eight figures (shapes) for testing and five figures as a
possible answer. In SUS the matrix pattern is
transformed into the series of the eight test figures
8,..1, =iv
i
and for each figure the symbolic name
8,..1, =i
i
η
is obtained during the visual reasoning.
The symbolic name
i
η
is transformed into the string
form
S
i
℘ . As it was described in the previous
chapter, the string form consists of the combination
of the selected letters, numbers and the symbol “|”.
The string has a following form: B1|…|Bi|...|Bn|,
where Bi denotes the symbolic names of the class.
The test string form is given as follows:
1. A11|A21|….|An11|
2. A12|A22|….|An22|
3. A13|A23|….|An33|
4. A14|A24|….|An44|
5. A15|A25|….|An55|
6. A16|A26|….|An66|
7. A17|A27|….|An77|
8. A18|A28|….|An88|
The answer string form is given as follows:
1. B11|B21|….|Bn11|
2. B12|B22|….|Bn22|
3. B13|B23|….|Bn33|
4. B14|B24|….|Bn44|
ICINCO 2005 - ROBOTICS AND AUTOMATION
416

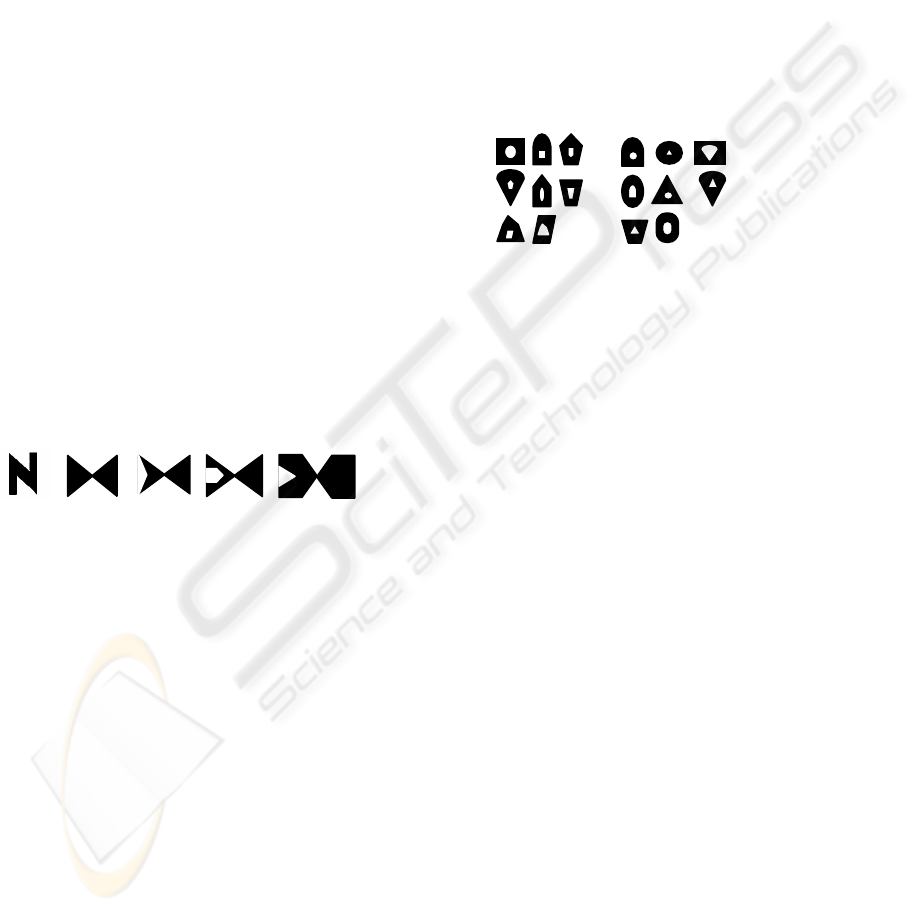
5. B15|B25|….|Bn55|.
4.1 Representation and
Generalization
The symbolic name
8,..1, =i
i
η
that is obtained
during visual reasoning refers to one of the symbolic
representations. SUS gives the symbolic
representation in the SUS notation that includes all
possible symbolic representations (on all levels of
descriptions).
This notation is transformed into the basic form by
the ClassDescriptionExpert. The basic form includes
symbols that refer to the symbolic names (general
level of description). In this example, the string is
transformed into the form
Q<L4>[R]|<L3>[A]<L3>[A]| that refers to the
symbolic notation
)2(
32
4
A
L
LQ
R
. There are classes such
as the complex class that have two synonymous
symbolic names. For example, the symbolic names
for the archetypes shown in Fig.4 b,c,d,e are as
follows: Fig b
),()2(
3332
4
AAO
L
LLDLQ
R
≡
, Fig.c
))(,()3(
31333
34
O
L
AO
L
LQLDLQ
AR
≡
, Fig.d
))(,()2(
513533
34
M
L
AMO
L
LQLDLLQ
AR
≡
, Fig.e
))(,()3(
31533
54
A
L
MA
L
LQLDLQ
MR
≡
,.
a b c d e
Figure 4: Exemplars from the concave class a. and from
the complex classes b,c,d,e
In the case of the complex class the SUS selects at
first the complex representation that is transformed
into string form and if the solution is not found, the
concave class representation is used. The Q
representation (does not give the solution) and the
representation D (gives the solution) is as follows:
1.Q3|L4R|L3A|L3O|L3O| 1.D2|Q1|L3A|L3A|L3A|
2.Q3|L6U|L3O|L3O|L4R| 2.D2|Q1|L4R|L4R|L4R|
3.Q3|L4R|L3A|L3A|L5M| 3.D2|Q1|L5M|L5M|L5M|
4.Q3|L6U|L3O|L3O|L5M| 4.D2|Q1|L4R|L5M|L4R|
5.Q3|L4R|L3A|L3A|L3A| 5.D2|Q1|L5M|L3A|L5M|
6.Q3|L4R|L3O|L3O|L4R| 6.D2|Q1|L3A|L4R|L3A|
7.Q3|L4R|L3A|L3A|L4R| 7.D2|Q1|L5M|L4R|L5M|
8.Q3|L4R|L3O|L3O|L5M| 8.D2|Q1|L3A|L5M|L3A|
Solution consists of three possible configurations:
1.D2|Q1|L4R|L3A|*|,
2.D2|Q1|*|L3A|L4R| and
3.D2|Q1|L4R|L3A|L4R|.
4.2 Generalization
Translation of the symbolic name into a string form
requires including all details of the symbolic name.
The level of details is marked by introducing the
symbol ”_”. The symbolic name is translated into
the form L0_L1_...Ln, where the level Ln denotes
the level of the detailed description of the archetype
of the class. The test that is converted into the string
form needs to preserve the level of details. The n-th
level of details can be written in the string form as
follows:
|_...|...|_...|...|_...
0
1
0
1
0
1
H
n
H
ii
H
jAjAjAjAjAjA Exa
mples of the test for one and two levels of details are
given in Fig. 5.
Figure 5: The first level of generalization and the second
level of generalization
A_1|L4_R|L5_T| A_1_*|M_1_L4R|K_1_C|
A_1|L3_O|L4_R| A_1_*|K_1_C |L_3_A|
A_1|L5_Y|L3_O| A_1_*|L_4_R |M_1_L3A|
A_1|L3_A|L3_A| A_1_*|K_1_E |M_1_L4R|
A_1|L5_M|L5_M| A_1_*|L_3_A |K_1_C|
A_1|L4_R|L4_Y| A_1_*|M_1_L3A|L_3_A|
A_1|L5_O|L4_T| A_1_*|L_4_T |L_3_A|
A_1|L4_T|L3_A A_1_*|M_2_L4R|M_2_L4R|
Solution test 1. A_1|L3_*|L5_*|, and
test 2. A1|
K_*_*|K_*_*|
During generalization the symbol is dropped from
the left to the right. For example, for the test in Fig
5a the first level of generalization (the first raw) is
A|L4|L5|. For the test in Fig. 5b the first level of
generalization (the first raw) is A_1|M_1|K_1| and
the second level of generalization is A|M|K|. The
generalization is performed by the
TestGeneralizationExpert.
5 SHAPE UNDERSTANDING
SYSTEM
The shape understanding system consists of the main
reasoning module and the peripheral modules for
performing the special tasks such as solving the
visual intelligence test. The test is solved by part of
the peripheral module called the test solver that
consists of the SymbolicNamesTestConverterExpert,
the StringFormConverterExpert,
the TestIdentificationExpert,
the CompatibilityFormExpert,
SUS A NEW GENERATION THINKING ROBOTS - The Visual Intelligence Tests
417

the TestGeneralizationExpert and the specialized test
solver experts. The schema of the test solver that is
part of the peripheral module of SUS is shown in
Fig. 6. In this paper only the solver expert for
progressive matrices test is presented. The test is
solved by following algorithm.
Algorithm: General test solving algorithm
1. Make the visual reasoning and find the symbolic name
for each figure in the test during the visual reasoning
2. Invoke the SymbolicNamesTestConverterExpert to
find the basic symbolic name representation
3. Invoke the StringFormConverterExpert to find the test
string form
4. Invoke the TestIdentificationExpert to find the type of
the test
5. Invoke the specialized test solver experts to find the
solution
6. if solution not found invoke the
TestGeneralizationExpert and goto 4.
7. END.
Figure 6: Schema of the SUS peripherals modules for
performing the task solving the visual intelligence test
The TestIdentificationExpert and the specialized test
solver expert implements algorithms for solving the
test. In the next chapter an algorithms that are
implemented in the TestIdentificationExpert and two
test solver experts (TestAOExpert and
TestFRExpert) are described.
5.1 TestAOExpert
The TestAOExpert implements solution for the test
type AO. The test AO is given in the form of the
eight figures that are transformed into the symbolic
names and next into the string forms. In this paper
the string forms of the tests is restricted to the type S
given in the form Sn|A|1X|…|iX|…|nX|. The test AO
is given in the form:
1.Sn1|A|1X|…|iX|…|n1X
2.Sk1|A|1X|…|iX|…|k1X
3.Sm1|A|1X|…|iX|…|k1X
4.Sn2|A|1X|…|iX|…|n2X
5.Sk2|A|1X|…|iX|…|k2X
6.Sm2|A|1X|…|iX|…|k2X
7.Sn3|A|1X|…|iX|…|n3X
8.Sk3|A|1X|…|iX|…|k3X
Fig. 7 shows two tests that consist of exemplars
from cyclic classes. Example of the test given in Fig
7 is as follows:
1.A3|K1C|K1C|K1C| 1.A2|K1C|K1C|* |* |
2.A2|L4R|L4R |* | 2.A2|L4R|L4R |* |* |
3.A1|K1C|* |* | 3.A4|L4R|L4R |K1C|K1C|
4.A1|K1C|* |* | 4.A1|K1C|* |* |* |
5.A3|L4R|L4R |L4R | 5.A1|L4R|* |* |* |
6.A2|L4R|L4R |* | 6.A2|L4R|K1C|* |* |
7.A2|K1C|K1C|* | 7.A2|K1C|K1C|* |* |
8.A1|L4R|* |* | 8.A1|L4R |* |* |* |
The possible solution found by SUS for test 1:
A1|K1C|* |* | and for test 2:
A3|L4R|K1C|K1C|* |.
Figure 7: Example of tests type AO
The two rows are used to find the relationships
between numbers of figures F1 and F2 and the third
raw is used to find the solution. The relationships:
(m1-n1)+(m2-n2)=(m3-n3) and (m4-n4)+(m5-
n5)=(m6-n6) are used to find if the test is type AO.
At first the type of string is checked and if the type
of test is S the relationships are checked. If both
conditions are fulfilled the test is type AO. The
TestIdentificationExpert implements part of
algorithms that check if the algorithm is type AO. If
so, the TestAOExpert is invoked to find the solution.
In the first stage of the algorithm the test is checked
if it is of type AO, next the possible solution is
found and finally the possible solution of the test is
matched with the given answers.
The TestIdentificationExpert implements an
algorithm to check if the test type is
AB
ℑ . In the
first stage the type of the test symbols
)(
T
ij
℘Θ is
computed. The test AB is given as the set of strings
||...||...|||
1
j
n
j
i
jj
j
n
XXXAS , where
},{
21
ηη ∈
i
X
denotes the symbolic names of parts
of the figures of the tests. The type of the test
symbols )(
T
ij
℘Θ is the number of the different
symbolic names
mi
η
η
η
,......,
1
in the test
T
ij
℘ . The
type of the test symbols
)(
T
ij
℘Θ
is computed by
SUS MMod
VisT
hi n
Nat
lL
a
nD
ClassDes
Strin
g
For
S
y
mbolicName
ConceptDesc
TestIdentifica
TestAOE
TestFREx
TestBCEx
TestBCEx
DiscrTest
An
swe
rEx
TestGenerExp CompFormEx
ICINCO 2005 - ROBOTICS AND AUTOMATION
418

counting the number of the different symbolic
names.
Compute type of the test symbols )(
T
ij
℘Θ
begin
For i=2 to n
begin
Xthanif
T
ij
T
ij
=℘≠℘ '*'
For j=0 to 7
begin
thanXif
T
ij
=℘
begin
T
ij
L ℘=
Θ
, 1+Θ=Θ , '*'=
℘
T
ij
,
end
end
end.
An algorithm ‘Check_if _test_ type_is_ type
AB
ℑ ’
is implemented as a part of the
TestIdentificationExpert.
Check_if _test_ type_is_ type
AB
ℑ
begin
1. For each object in the test pattern
T
i
Oo ∈
the
visual name
T
i
η is obtained and transformed
into a string
T
ij
℘ (Sn|A|1X|…|iX|…|nX| )
2. The type of the test symbols
)(
T
ij
℘Θ is
computed
3. 2)( >℘Θ
T
ij
if than goto END.
For i=2 to n
Begin
For j=0 to 7
Begin
11
0
−===℘
ijij
T
ij
nelsenthanLif
end
end
For j=0 to 7
begin
∑
=
=
n
i
ij
j
nS
2
end
if
210
SSS =+ and
5
43
SSS =+ then
1=ℑ
AB
END
end.
TestAOExpert implements an algorithm to
compute the solution
‘Compute_solution_test_
AB
ℑ ’.
Algorithm: Compute_solution_test_
AB
ℑ
begin
1. For j=0 to 7
begin
∑
=
=
n
i
ij
j
nS
2
end
7
6
SSS +=
2. Decompose S into the type of the class, next into
symbolic names X1..Xh and next into form of
possible solution S|A|1X|…|iX|…|hX
3. For each object from a set of given answers A,
Au
i
∈
obtain the visual name
A
i
η and transform it
into form Sn|A|1X|…|iX|…|nX|
4. Find the final solution by string matching between
the string of the given answers and the possible
solution
end.
5.2 Test FR Expert
The TestFRExpert implements algorithms that give
solution to the test FR. In order to have solution the
test needs to have at least two features in common
for each three figures. The figures are arranged in
such a way that six figures are used to find the
general rules of prediction and two figures are used
to find the possible solution. The following pattern
(letters F1…F8) shows the figure in the test
F1 F2 F3
F4 F5 F6
F7 F8 F?.
There are two configurations used in the test. The
simple configuration CS is given as three sets of the
three figures {F1, F2, F3}, {F4,F5,F6}, {F7,F8, F?}.
The most common configuration CMC is given as
{F1,F6,F8}, {F3,F5,F7}, {F2, F4, F?}. Each test
given in the form of the CMC configuration can be
transformed into CS configuration. Example of the
transformation is given in Fig. 8.
Figure 8: Transformation of the test given in the CMC
form into the CS form
SUS A NEW GENERATION THINKING ROBOTS - The Visual Intelligence Tests
419

5.3 Features
Test is solved by selecting features for both
configurations {F1,F6,F8} and {F3,F5,F7}. The
feature is any symbol in the string representation
…|X1|…|Y1|.... The relationships can be formulated
in the form of one, two or more than two features.
Fig. 9 shows a test that has relationships expressed
in the form of the one feature (Fig. 9a) and two
features (Fig. 9b).
A1|M2L4R|M1L4R | Q1|M1L4R|Q1|L4R|M1 |
A1|M1L4R|M2L4R | Q1|L4R |Q1|L4R|L4R|
A1|M1L3A|M1L3A | Q1|L5M |Q1|L4T|L3A|
A1|M1L4R|M1L3A | Q1|L4R |Q1|L4T|L3A|
A1|M1L3A|M1L4R | Q1|L5M |Q1|L4R|M1 |
A1|M2L4R|M2L4R | Q1|M1L4R|Q1|L4R|L4R|
A1|M1L3A|M2L4R | Q1|L5M |Q1|L4R|L4R|
A1|M2L4R|M1L3A Q1|M1L4R|Q1|L4T|L3A|
Solution for the first test is A1|M1L4R|M1L4R| and
for the second test is
1.Q1|L4R|Q1|*|M1|
2.Q1|L4R|Q1|L4R|M1|.
Figure 9: Tests that have relationships expressed in the
form of the one feature (a) and two features (b)
In this paper algorithm is presented in the context of
the most common configurations. This form is used
to design the algorithm for finding the solution to the
test. The test which has solution can be written as
follows:
1. …|X1|…|Y1|... 1. X1|Y1
2. …|X2|…|Y2|... 2. X2|Y2
3. …|X3|…|Y3|... 3. X3|Y3
4. …|X2|…|Y3|... 4. X2|Y3
5. …|X3|…|Y1|... or in short 5. X3|Y1
6. …|X1|…|Y2|... 6. X1|Y2
7. …|X3|…|Y2|... 7. X3|Y2
8. …|X2|…|Y3|... 8. X2|Y3
The test can be given in the compatible form that
means each eight rows have the columns that are
representative of the same type of classes. The test
given in the compatible form can be represented as
follows:
1A1|1A2|…|1Ai|…|1An|
2A1|2A2|…|2Ai|…|2An|
3A1|3A2|…|3Ai|…|3An|
4A1|4A2|…|4Ai|…|4An|
5A1|5A2|…|5Ai|…|5An|
6A1|6A2|…|6Ai|…|6An|
7A1|7A2|…|7Ai|…|7An|
8A1|8A2|…|8Ai|…|8An|
The test is formulated as the pattern of the eight
strings. For simplicity the type of compatible test
can be written in the form of the one string.
Examples of the different one string representation
of the different tests are as follows:
Sn|A|1X|…|iX|…|nX|, S1|A|1_S1|1_A|1_X|,
Sn|A|1X|2X|…|hX|1_1Q1|1_1G|1_R|…|1_hQ1|1_hG
|1_hR|.
The incompatible test can be represented as follows:
1A1|1A2|…|1Ai|…|1An1|
2A1|2A2|…|2Ai|…|2An2|
3A1|3A2|…|3Ai|…|3An3|
4A1|4A2|…|4Ai|…|4An4|
5A1|5A2|…|5Ai|…|5An5|
6A1|6A2|…|6Ai|…|6An6|
7A1|7A2|…|7Ai|…|7An7|
8A1|8A2|…|8Ai|…|8An8|
The transformation from the incompatible form into
the compatible form is performed by the
CompatibilityFormExpert. The transformation from
the incompatible form into the compatible form
involves both type of the classes and the symbolic
names. At first the type of the class for each row is
compared to find if it can be transformed into the
compatible form. If the incompatible form can be
transformed into the compatible form at first the
types of class for each row are matched with the test
general type of the class. The test general type of
class is the type that makes it possible to fit structure
of all strings. The general type can be generated or
stored as a template. For example, the test Sn can
contain string type Qn|G|1R|…|iR|…|nR|,
An|C|1W|…|iW|…|nW| or both type of strings. For
the type Snj|A|1X|…|iX|…|nX| the algorithm is as
follows:
For j=1 to 8
begin
if nj<n2 than
begin
for nj+1 to n2
begin
jX=’*’
end.
Example of the test type Sn is as follows:
|Q2|L4R|L3A|L4R|* |
|Q1|L3A|L4R|* |* |
|Q2|L5M|L3A|L4T|* |
|Q3|L3A|L3A|L4T|L5M|
|Q1|L5M|* |* |* |
|Q2|L4R|L3A|L4R|* |
|Q3|L5M|L3A|L4R|L5M|
|Q2|L4R|L3A|L3A|* |
Similarly the procedure can be applied for the test
type S11_S given as:
|_1|...|_1|_1|_1|....|_1|...|_1|_1|_1||
1
1
1
1
1
1
11
1 mn
nnn
mnmmn
XXASXXASAS
In
the test we assume that n, m1 and mn are <5. In the
test where the different types are included the
numbers of features are limited by the perceptual
abilities of SUS. The TestIdentificationExpert
implements an algorithm to check if the test is of
ICINCO 2005 - ROBOTICS AND AUTOMATION
420

type
FR
ℑ . Procedure combi_n_m(n,k) computes the
k combinations from the set of n numbers.
Procedures ComputeSUM3() and
ComputeSUMP1_P2() compute the number of the
relationships between the characteristic features of
the test.
ComputeSUM3()
Begin
S=0;
1
10
+=℘=℘ SSthanif
SS
1
20
+=℘=℘ SSthanif
SS
1
21
+=℘=℘ SSthanif
SS
SA
Z
ik
=
End.
ComputeSUMP1_P2()
Begin
S=0
1
50
+=℘=℘ SSthanif
SS
1
70
+=℘=℘ SSthanif
SS
1
31
+=℘=℘ SSthanif
SS
1
42
+=℘=℘ SSthanif
SS
1
62
+=℘=℘ SSthanif
SS
SA
S
ik
=
1
S=0
1
40
+=℘=℘ SSthanif
SS
1
51
+=℘=℘ SSthanif
SS
1
61
+=℘=℘ SSthanif
SS
1
32
+=℘=℘ SSthanif
SS
1
72
+=℘=℘ SSthanif
SS
SA
S
ik
=
2
End.
The Checkif Test _is _type FR () algorithm checks if
the test type is type
FR
ℑ .
Checkif Test _is _type FR ()
begin
0=
i
s
For i=0 to n
begin
For j=1 to 7
begin
1
0
+=℘=℘
ii
T
ij
T
i
ssthanif
For i=0 to n
begin
columnthiremovethansif
i
−= 8
end
for k=1 to 2
begin
m_N=combi_n_m(n,k)
for i=0 to n
begin
for j=0 to 2
begin
0i
Ca
=
,
1i
Cb
=
,
R
bj
R
aj
S
j
℘⊕℘=℘
end
ComputeSUM3()
for i=0 to n
begin
thanAif
Z
i
0=
begin
S=0
for j=0 to 7
begin
0i
Ca
=
,
1i
Cb
=
R
bj
R
aj
S
j
℘⊕℘=℘
end
ComputeSUMP1_P2()
end
end
for i=0 to n
begin
thanAandAif
S
ik
S
ik
)55(
21
== 1=ℑ
Fr
end
end
The expert SolveTestAA implements an algorithm
SolveTestAA(). An algorithm finds the solution and
transforms it into the string form.
SolveTestAA()
begin
s1=0, s2=0
for i=0 to n
begin
thanAif
S
i
5
1
0
=
begin
SUS A NEW GENERATION THINKING ROBOTS - The Visual Intelligence Tests
421

R
i
SA
s
℘=℘
1
, s1=s1+1
end
thanAif
S
i
5
2
0
=
begin
R
i
SB
s
℘=℘
2
, s2=s2+1
end
for i=0 to m_N
begin
0i
Ca = ,
1i
Cb =
thanAif
S
i
5
1
1
=
begin
11
1
R
b
R
a
SA
s
℘⊕℘=℘ , s1=s1+1
end
thanAif
S
i
5
2
1
=
begin
11
2
R
b
R
a
SB
s
℘⊕℘=℘
, s2=s2+1
end
end.
6 EXPERIMENT AND
DISCUSSION OF THE
RESULTS
The method of shape understanding was
implemented as a shape understanding system
(SUS). The shape understanding system (SUS) (Les
2004) is implemented in C++ under Windows 2000
on 3.06 GHz Pentium computer. In this paper
understanding abilities of the shape understanding
system are tested based on the intelligence tests. The
SUS intelligence tests are formulated as the tasks
given to the system.
In the experiment the progressive matrices test was
used. In this experiment the task was formulated as:
‘find the object
5,..1, =ko
k
that fills the missing
entry in the matrix
3,..1,,
,
=jiv
ji
:
σ >
k
ji
kk
okjiforvoo ⇒==⊗∃ ]5,...,13,..1,,:[
,
The
progressive matrices test consist of the eights matrix
objects and five objects from which one was to be
selected. The digital objects were obtained by
generating exemplars from selected classes or by
digitizing 2-D visual objects on a 256 x 256 pixel
picture plane. The selection criterion is that the
selected object fills the missing entry in the matrix.
The test is presented to SUS as the sequence of the
eight figures (the test) and the five figures as the
answer. At first the symbolic names are obtained for
each figure and next the test was performed by
module called the test solver. During the testing
stage the following tasks were tested: testing the
general abilities of the SUS, testing the
generalization abilities of SUS and testing the
different levels of difficulties.
For testing general abilities of SUS the tests AO and
FR were used. In this experiment SUS needed to
identify the type of test and next to find the solution.
Solving these two different types of tests required
the proper identification of the type of the test. In
this experiment the algorithms that were used to
identify the type of the test were implemented as the
part of the TestIdentificationExpert. In this
experiment ten tests of the type AO and ten tests of
the type FR were used. Examples of tests of the type
AO are shown in Fig 10 and examples of tests of the
type FR are shown in Fig 8 and 9. The solution in
the form of the symbolic name that was found by
SUS was compared with the solution that was
obtained during the analysis of the test. The result
obtained by SUS was in agreement with results
obtained during the analysis of the test.
Figure 10: Examples of the tests of type AO
Testing ability to solve the test of the different levels
of difficulties was performed on the test of the type
FR. In this experiment the tests were grouped into
three groups: the easy, the medium and the difficult.
The level of difficulty of the test was found by
analyzing of the perceptually relevant features and
tested for small sample of human subjects. Tests
with the different levels of difficulty were presented
to SUS as a sequence of the eight figures. In this
experiment 30 tests of the type FR were used.
Examples of the tests used in the experiment are
shown in Fig. 9-10. During the performance, time
that was needed to solve the test was used as a
measure of the level of difficulty.
An ability to make generalization was performed on
two groups of tests. In the first group the first level
of generalization was tested, whereas in the second
group the second level of generalization was tested.
The tests were given as a series of figures and
solution was determined based on the properties of
ICINCO 2005 - ROBOTICS AND AUTOMATION
422

the test. Each group of tests consisted of five tests.
Examples of the test are shown in Fig. 11. Results
obtained by SUS were in agreement with results
obtained during the analysis of the test.
Figure 11: I level of generalization and (a,b) [f1] and II
level of generalization (c) [f1]
Progressive matrices test requires good abilities of
visual understanding. SUS needs to find the
representation that shows only relevant features of
the test. At first each figure is converted into
symbolic names and next into strings. Strings, after
refinements, are used to find the final solution.
Testing general abilities of the SUS required
identifying the type of the test and next finding the
solution. In the experiment two different types of
tests were used: the test of the type AO and the test
of the type FR. Solving these two different types of
tests required the proper identification of the type of
the test. Although a number of types of tests could
be large the method that was proposed would
incorporate identification of the different types of
tests. It would require implementing the proper
algorithm in the TestIdentificationExpert. The
algorithms for identification of the type ECW and
the type GA were elaborated and partially tested.
The result shows that proposed algorithm that was
implemented as the part of the
TestIdentificationExpert gives a very good results in
identifying and solving visual tests. The results
indicated that the visual tests can be performed in
two steps: the test identification and finding the
solution. The human subject also seems to perform
the test solving in two steps. However, finding the
type of the test does not guarantee that the human
subject will be able to solve the test.
Testing ability to solve the test of the different levels
of difficulty was performed on the tests of the type
FR. The time performance depended both on the
reasoning process that led to obtaining the symbolic
names and the time in which the test solver solved
the test given in the string forms. The reasoning
process is part of all tasks that are performed by
SUS and the time that is needed to obtain the
symbolic names is characteristic for the perceptual
abilities of SUS. The main indicator of the level of
difficulty is the time in which problem solver solves
the test. In the SUS for all tests presented there is
indication that time performance depends on the
level of difficulty. The time performance of the task
seems to be indicator of the test difficulty, however
the differences between the levels of difficulty are
not very significant. Human subject solves these
tasks in the different way. The levels of difficulty
are an indicator of the human ability to solve the
visual task. The tests that were ranked difficult were
not solved by all human subjects. Although in the
testing of the human subject a small sample was
used the result indicates that there is a big difference
in solving these tasks by human and by SUS. The
main reasons seem to be that SUS has a very good
string representation of the task. Even the test which
was classified as difficult was solved by SUS. It
indicates that for each tests that can be represented
by the string representation shown in this paper the
level of difficulties can be measured by time of
performance of the test. In comparison to the human
subject who after training process has its
performance very depending on the level of the test
difficulty, the SUS performance vary only in the
time that is needed to process the bigger number of
calculations.
An ability to make generalization was performed on
two groups of tests. All tests were solved by SUS
assuming that the generalization was performed in
ordered manner that means it takes into account the
known structural features of the exemplar.
Generalization requires knowledge of the class
description as well as knowledge of the geometrical
properties of the visual figures. In the case of SUS
the symbolic name that is the result of the visual
reasoning includes description of the class that refers
to the geometrical properties of figures. The
hierarchical structure of the shape classes make it
possible to perform generalization based on the
string representation. The combinatorial manners
that do not distinguished between the types of the
class descriptions require interpretation of the string
which was selected. The proposed method makes it
possible to perform complex generalization based on
the hierarchical structure of the shape classes.
7 CONCLUSION
In this paper understanding abilities of the shape
understanding system (SUS) are tested based on the
adoption of the intelligence tests. The intelligence
tests are formulated as the tasks given to the system.
Performance of the SUS was compared with the
human performance of these tasks. The results show
that the SUS is able to perform visual tasks that are
performed by the human observer during
intelligence tests. The tests were based on the
SUS A NEW GENERATION THINKING ROBOTS - The Visual Intelligence Tests
423

progressive matrices test which requires the good
visual problem solving abilities of the human
subject. SUS solves these tests by transforming the
visual form into the string form. The proposed string
form makes it possible to perform complex visual
reasoning.
The experiment proved that the proposed method,
which is part of the SUS visual understanding
abilities, can solve the test that is very difficult for
human subject.
The main novelty of the proposed method is that all
tasks performed by SUS applied their internal
representations called the visual concepts. The visual
concept in the case of the visual test refers to the
string representation of the test pattern.
REFERENCES
Bhanu, B., and Faugeras, O.D. (1984). "Shape Matching
of Two-Dimensional Objects." IEEE Transactions on
Pattern Analysis and Machine Intelligence 6(2): 137-
156.
Colaruso, R., and Hammil, D. (2003). Motor Free Visual
Perception Test. New York, Academic Therapy
Publications.
Gardener, M. F. (1996). Test of Visual-Perceptual Skills,
Psychological and Educational Publicatios.
He, Y., and Kundu, A. (1991). "2-D Shape Classification
Using Hidden Markov Model." IEEE Transactions on
Pattern Analysis and Machine Intelligence 13(11):
1172-1184.
Kartikeayan, B., and Sarkar, A. (1989). "Shape
Description by Time Series." IEEE Transactions on
Pattern Analysis and Machine Intelligence 11(9): 977-
984.
Les, Z. (2002). "Shape Understanding System:
Understanding the thin object." An
International
Journal Computers and Graphics 26(6): 951-970.
Les, Z., and Les, M. (2003). "Shape Understanding
system: Understanding of the Convex Objects." The
Journal of Electronic Imaging 12(2): 327-341.
Les, Z., and Les, M. (2004). "Shape Understanding
System-the System of Experts." International Journal
of Intelligent Systems 19(10): 949-978.
Les, Z., and Les, M. (2005). "Shape Understanding
System: Understanding of the Complex Object." The
Journal of Electronic Imaging (in print) 14(2).
Les, Z., and Les, M. (2005). "Understanding of a Concave
Polygon Object in Shape Understanding System."
Journal of Computer and Graphics 29(3): 365-378.
Lu, C. H., and Dunham, J.G. (1993). "Shape Matching
Using Polygon Approximation and Dynamic
Alignment." Pattern Recognition Letters 14: 945-949.
Pal, N. R., Pal, P., and Basu, A.K. (1993). "A New Shape
Representation Scheme and Its Application to Shape
Discrimination Using a Neural Network." Pattern
Recognition 26(4): 543-551.
Pope, A. R. (1994). Model-based Object Recognition, a
Survey of Recent Research, Department of Computer
Science, The University of British Columbia.
ICINCO 2005 - ROBOTICS AND AUTOMATION
424