
A NEW FAMILY OF CONTROLLERS FOR POSITION CONTROL
OF
ROBOT MANIPULATORS
∗
Fernando Reyes, Jaime Cid, Marco Mendoza, Isela Bonilla
Benem
´
erita Universidad Aut
´
onoma de Puebla
Grupo de Rob
´
otica, Facultad de Ciencias de la Electr
´
onica
Apartado Postal 542, Puebla 72001, M
´
exico
Keywords:
Lyapunov function, Global asymptotic stability, PD and PID controllers, Direct-drive robots, position control.
Abstract:
This paper addresses the problem of position control for robot manipulators. A new family of position con-
trollers with gravity compensation for the global position of robots manipulators is presented. The previous
results on the linear PD controller are extended to the new proposed family. The main contribution of this
paper is to prove that the closed–loop system composed by full nonlinear robot dynamics and the family of
controllers is globally asymptotically stable in agreement with Lyapunov’s direct method and LaSalle’s in-
variance principle. Besides the theoretical results, a real-time experimental comparison is also presented on
visual servoing applications to illustrate the performance of the proposed family on a direct–drive robot of two
degrees of freedom.
1 INTRODUCTION
The position control of robot manipulators, or also the
so-called regulation problem is the simplest aim in ro-
bot control and at the same time one of the most rele-
vant issue in practice of manipulators. This is a partic-
ular case of the motion control or trajectory control.
The primary goal of motion control in joint space is to
make the robot joints track a given time-varying de-
sired joint position. On the other hand, the goal of
position control is to move the robot end-effector to
a fixed desired target, which is assumed to be con-
stant, regardless of its initial joint position (Craig,
1989)(F. L. Lewis, 1993)(O. Khatib, 1989).
The PD control is the most widely used strategy
for robot manipulators, because of its simplicity, it
counts with theoretical support to justify the use of the
PD in global positioning (M. Takegaki, 1981)(S. Ari-
moto, 1986)(C. Canudas, 1996). On the other hand,
the PID control is another popular strategy, until now
we do not have the required theoretical support back-
ing to guarantee position control in a global sense
(Kelly, 1995)(R. Kelly, 1996)(Kelly, 1999)(Y. Xu,
1995)(V. Santiba
˜
nez, 1998).
However, the PD control with gravity compen-
sation has serious practical drawback, for example:
∗
Work partially supported by VIEP-BUAP III-66-04
ING/G MEXICO
it requires the exact knowledge of the gravitational
torque vector from robot dynamics. Although the
structure of the gravitational torque vector can be eas-
ily obtained as the gradient of the robot potential en-
ergy due to gravity, some parameters can be uncertain
such as masses and mass centers. Other draws is that
the choice of the PD gains relies on the desired posi-
tion (J. Alvarez, 2003)(A. Loria, 2002)(L. Sciavicco,
1996).
In recent years, various PD-Type control schemes
have been developed for position control of robot ma-
nipulators. Among them the following can be cited: A
PD controller with proportional and derivative gains
as nonlinear functions of the robot states developed
in (Y. Xu, 1995). In the reference (V. Santiba
˜
nez,
1998) was proposed a Saturated PD controller to de-
liver torques within prescribed limits according to the
actuator capability. A new class of nonlinear PID
controllers with robotic applications was presented in
(Seraji, 1998). (Kelly, 1999) presented a PD con-
troller in generic task space. This controller was
based on energy shaping methodology. Most recently,
(J. Alvarez, 2003) proposed a saturated linear PID
controller with semiglobal stability.
In view of the simplicity and applicability of the
simple PD controller in industrial applications, the
main motivation of this paper is in the theoretical and
practical interest of obtaining controllers that lead to
361
Reyes F., Cid J., Mendoza M. and Bonilla I. (2005).
A NEW FAMILY OF CONTROLLERS FOR POSITION CONTROL OF ROBOT MANIPULATORS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 361-366
DOI: 10.5220/0001174803610366
Copyright
c
SciTePress

global asymptotic stability of the closed-loop system.
The objective of this paper is to extend the previous
results on the linear PD controller to a new family of
position controllers. In addition to the theoretical is-
sues of the proposed family, this paper also presents
real-time experiments for position control on a direct-
drive robot of two degrees of freedom.
This paper is organized as follows. Section 2 re-
calls the robot dynamics and useful property for sta-
bility proof. In the Section 3, the new family of posi-
tion controllers and its analysis of global asymptotic
stability is presented. Section 4 summarizes the main
components of the experimental set-up. Section 5
contains the experimental results. Finally, some con-
clusions are offered in Section 6.
2 ROBOT DYNAMICS
The dynamics of a serial n-link rigid robot can be
written as (L. Sciavicco, 1996)(Vidyasagar, 1989):
M(q)
¨
q + C(q,
˙
q)
˙
q + g(q) + f (
˙
q, τ ) = τ (1)
where q is the n × 1 vector of joint displacements;
˙
q
is the n × 1 vector of joint velocities; τ is the n × 1
vector of input torques; M(q) is the n × n symmetric
positive definite inertia matrix, C(q,
˙
q) is the n × n
matrix of centripetal and Coriolis torques; g(q) is the
n × 1 vector of gravitational torques and f (
˙
q, τ ) is
the n × 1 vector for the friction torques. The vector
f(
˙
q, τ ) is decentralized in the sense that f (
˙
q, τ )
depends only on ˙q
i
and τ
i
; that is,
f (
˙
q, τ ) =
f
1
( ˙q
1
, τ
1
)
f
2
( ˙q
2
, τ
2
)
.
.
.
f
n
( ˙q
n
, τ
n
)
.
The friction torques f(
˙
q, τ ) are assumed to
be dissipate energy at all non-zero velocities, and
therefore, their entries are bounded within the first
and third quadrants. This feature allows to consider
the Coulomb and viscous friction common models.
At zero velocities, only static friction is present
satisfying:
f
i
(0, τ
i
) = τ
i
− g
i
(q)
for -
¯
f
i
≤ τ
i
− g
i
(q) ≤
¯
f
i
, with
¯
f
i
being the limit on
the static friction torques for joint i (B. Armstrong-
Ho
´
elouvry, 1999)(Armstrong-Ho
´
elouvry, 1991).
It is assumed that the robot links are joined
together with revolute joints. Although the equation
of motion (1) is complex, it has several fundamental
properties which can be exploited to facilitate control
system design. For the new controller, the following
important property is used:
Property 1. The matrix C(q,
˙
q) and the time deriv-
ative
˙
M(q) of the inertia matrix satisfy (Vidyasagar,
1989)(Koditschek, 1984):
˙
q
T
1
2
˙
M(q) − C(q,
˙
q)
˙
q = 0 ∀ q,
˙
q ∈ IR
n
. (2)
3 A NEW FAMILY POSITION
CONTROLLERS
This section presents the new family of controllers and its
stability analysis. Consider the following control scheme
with gravity compensation given by
τ = ∇U(K
p
,
˜
q) − f
v
(K
v
,
˙
q) + g(q) (3)
where
˜
q = q
d
− q ∈ IR
n
is the position error vec-
tor, q
d
∈ IR
n
is the desired joint position vector,
K
p
∈ IR
n×n
is the proportional gain which is diag-
onal matrix, K
v
∈ IR
n×n
is a positive definite matrix,
also called derivative gain, U(K
p
,
˜
q) represents the ar-
tificial potential energy, positive de- finite function,
and f
v
(K
v
,
˙
q) denotes the damping function, which
is dissipative function, that is,
˙
q
T
f
v
(K
v
,
˙
q) > 0.
The control problem can be stated by selecting the
design functions U(K
p
,
˜
q) and f
v
(K
v
,
˙
q) such that the
position error
˜
q and the joint velocity
˙
q vanish asymp-
totically, i.e.,
lim
t→∞
[
˜
q(t),
˙
q(t)]
T
= 0 ∈ IR
2n
.
Proposition. Consider the robot dynamic model (1)
together with the control law (3), then the closed-loop
system is globally asymptotically stable and the posi-
tioning aim lim
t→∞
q(t) = q
d
∧ lim
t→∞
˙
q(t) = 0 is
achieved.
Proof: The closed-loop system equation obtained by
combining the robot dynamic model (1) and control
scheme (3) can be written as
d
dt
˜
q
˙
q
=
−
˙
q
M
−1
(q) [∇U(K
p
,
˜
q) − f
v
(K
v
,
˙
q)
−C(q,
˙
q)
˙
q]
(4)
which is an autonomous differential equation, and
the origin of the state space is its unique equilibrium
point.
ICINCO 2005 - ROBOTICS AND AUTOMATION
362
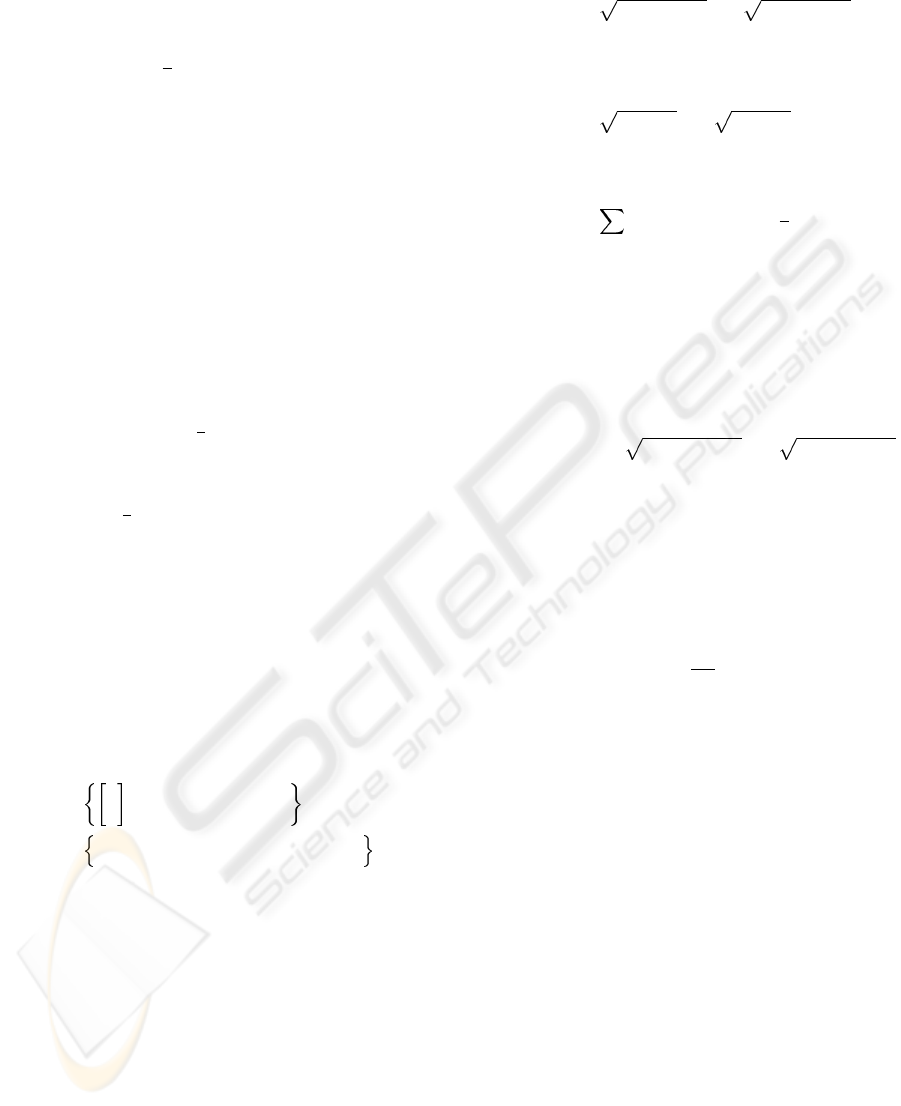
To carry out the stability analysis of equation (4),
the following Lyapunov function candidate is pro-
posed:
V (
˜
q,
˙
q) =
1
2
˙
q
T
M(q)
˙
q + U(K
p
,
˜
q). (5)
The first term of V (
˜
q,
˙
q) is a positive definite func-
tion with respect to
˙
q because M (q) is a positive def-
inite matrix. The second one of Lyapunov function
candidate (5), which can be interpreted as a potential
energy induced by the control law, also is a positive
definite function with respect to position error
˜
q, be-
cause terms K
p
and K
v
are positive define matrixes.
Therefore, V (
˜
q,
˙
q) is a globally positive definite and
radially unbounded function.
The time derivative of Lyapunov function candi-
date (5) along the trajectories of the closed-loop equa-
tion (4) and after some algebra and considering prop-
erty 1, can be written as:
˙
V (
˜
q,
˙
q) =
˙
q
T
M(q)
¨
q +
1
2
˙
q
T
˙
M(q)
˙
q − ∇U (K
p
,
˜
q)
T
˙
q
=
˙
q
T
∇U(K
p
,
˜
q) −
˙
q
T
f
v
(K
v
,
˙
q) − C(
˙
q, q)
˙
q
+
1
2
˙
q
T
˙
M(q)
˙
q − ∇U (K
p
,
˜
q)
T
˙
q
= −
˙
q
T
f
v
(K
v
,
˙
q) ≤ 0, (6)
which is a globally negative semidefinite func-
tion and therefore, it is possible to conclude sta-
bility of the equilibrium point. In order to prove
global asymptotic stability, the autonomous nature of
the closed-loop equation (4) is exploited to apply
the LaSalle’s invariance principle (Khalil, 2002) in
the region Ω:
Ω =
˜
q
˙
q
∈ IR
2n
:
˙
V (
˜
q,
˙
q) = 0
=
˜
q ∈ IR
n
,
˙
q = 0 ∈ IR
n
:
˙
V (
˜
q,
˙
q) = 0
,
since
˙
V (
˜
q,
˙
q) ≤ 0 ∈ Ω, V (
˜
q(t),
˙
q(t)) is a decreasing
function of t. V (
˜
q,
˙
q) is continuous on the compact
set Ω, it is bounded from below on Ω. For example,
it satisfies 0 ≤ V (
˜
q(t),
˙
q(t)) ≤ V (
˜
q(0),
˙
q(0)). There-
fore, the trivial solution is the unique solution of the
closed-loop system (4) restricted to Ω, then it is con-
cluded that the origin of the state space is globally
asymptotically stable.
Remark I. A simple Case of Study: Suppose that
the U(K
p
,
˜
q) =
˜
q
T
K
p
˜
q, and f
v
(K
v
,
˙
q) = K
v
˙
q then
the popular controller PD is generated:
τ = K
p
˜
q − K
v
˙
q + g(q). (7)
Remark II: Next, are presented several controllers,
generated all them of the following artificial potential
functions:
if U(K
p
,
˜
q) =
ln(cosh(
˜
q))
T
K
p
ln(cosh(
˜
q)) and
f
v
(K
v
,
˙
q) = K
v
tanh(
˙
q) then
τ = K
p
tanh(
˜
q) − K
v
tanh(
˙
q) + g(q)
if U(K
p
,
˜
q) = cosh(
˜
q)
T
K
p
cosh(
˜
q) and
f
v
(K
v
,
˙
q) = K
v
sinh(
˙
q) then
τ = K
p
sinh(
˜
q) − K
v
sinh(
˙
q) + g(q)
if U(K
p
,
˜
q) =
n
i=1
k
pi
[˜q
i
arctan(q
i
) −
1
2
ln (1 + q
2
i
)] and
f
v
(K
v
,
˙
q) = K
v
arctan(
˙
q) then
τ = K
p
arctan(
˜
q) − K
v
arctan(
˙
q) + g(q).
Remark III Jacobian Transpose Controller Ap-
proach: The position control in the space of Task-
Oriented coordinate proposed by (M. Takegaki, 1981)
can be address. A minor modification of the Lya-
punov function leads to:
if U(K
p
,
˜
x
r
) =
ln(cosh(
˜
x
r
))
T
K
p
ln(cosh(
˜
x
r
))
and f
v
(K
v
,
˙
q) = K
v
tanh(
˙
q) then
τ = J
A
(q)
T
R(θ)K
p
tanh(
˜
x
r
)
−K
v
tanh(
˙
q) + g(q)
where x
r
is the position of the robot in Cartesian
coordinates, given by the direct kinematics f and
J
A
(q) ∈ IR
n×n
is a Jacobian matrix, defined from di-
rect kinematics as:
J
A
(q) =
∂f
∂q
.
4 EXPERIMENTAL SET-UP
An experimental system for research of robot control
algorithms has been designed and built at The Uni-
versidad Aut
´
onoma de Puebla, M
´
exico; it is a direct-
drive robot of two degrees of freedom (see Figure 1).
The experimental robot consists of two links made
of 6061 aluminium actuated by brushless direct-drive
servo actuators from Parker Compumotor to drive the
joints without gear reduction. Advantages of this type
of direct-drive actuator includes freedom from back-
slash and significantly lower joint friction compared
with actuators composed by gear drives. The mo-
tors used in the robot are listed in Table 1. The ser-
vos are operated in torque mode, so the motors act
as a torque source and they accept an analog volt-
age as a reference of torque signal. Position infor-
mation is obtained from incremental encoders located
on the motors. The standard backwards difference al-
gorithm applied to the joint positions measurements
was used to generate the velocity signals. The manip-
ulator workspace is a circle with a radius of 0.7 m.
A NEW FAMILY OF CONTROLLERS FOR POSITION CONTROL OF ROBOT MANIPULATORS
363

Besides position sensors and motor drivers, the robot
also includes a motion control board manufactured by
Precision MicroDynamics Inc., which is used to ob-
tain the joint positions. The control algorithm runs on
a Pentium-II (333 Mhz) host computer.
Figure 1: Experimental robot.
Table 1: Servo actuators of the experimental robot.
Link Model Torque [Nm] p/rev
1. Shoulder DM1050A 50 1,024,000
2. Elbow DM1004C 4 1,024,000
With reference to our direct-drive robot, only the
gravitational torque is required to implement the new
family of controllers (3), which is available in (Kelly,
1997):
g(q) =
38.46 sin (q
1
) + 1.82 sin (q
1
+ q
2
)
1.82 sin (q
1
+ q
2
)
[Nm].
The vision system consists of a camera with a focal
length λ = 0.0048 [m] and a FPG-44 frame proces-
sor board. A black disc was mounted on end-effector,
the centroid of disc was selected as the object feature
point.
The CCD camera was placed in front of the robot
and its position with respect to the robot frame Σ
R
was o
C
= [0.15, −0.55, 0.55]
T
[m].
5 EXPERIMENTAL RESULTS
To support our theoretical developments, this Section
presents an experimental comparison of three position
controllers on a planar robot.
We select in all controllers the desired position in
the image plane as [u
d
v
d
]
T
= [500 355]
T
[pix-
els] and the following initial position [u(0) v(0)]
T
=
[360 400]
T
[pixels] and ˙q(0) = 0 [degrees/sec]. The
friction phenomena were not modeled for compensa-
tion purposes. The evaluated controllers have been
written in C language. The sampling rate was exe-
cuted at 2.5 msec. while the visual feedback loop was
at 33 msec.
Figure 2 shows the experimental results of the con-
troller
τ = J
T
A
(q)R(θ)K
p
tanh
Λ
˜u
˜v
− K
v
tanh (Λ
˙
q)
+g(q). (8)
The parameters of this controller were selected
as K
p
= diag{23.6, 3.95} [Nm/pixels
2
],
K
v
= diag{2.0, 0.2} [Nm-sec/degrees] and
Λ = diag{0.1, 0.1}. Figure 2 depicts the time
evolution of feature error vector [˜u ˜v]
T
. The transient
response is fast and it was around 0.6 sec. After
transient, both components of the feature position
error tend asymptotically to a small neighborhood of
zero( 3 and -1 pixels, respectively).
Figure 2: Feature position error trajectory in the image
plane for controller (8).
The experimental results for the controller
τ = J
T
A
(q)R(θ)K
p
arctan
Λ
˜u
˜v
− K
v
arctan (Λ
˙
q)
+g(q)
(9)
are shown in Figure 3. The proportional and deriv-
ative gains were selected as K
p
= diag{15.0, 2.8}
[Nm/pixels
2
], K
v
= diag{2.0, 0.1} [Nm-
sec/degrees] respectively and Λ = diag{0.1, 0.1}.
The transient response is fast and it was around 0.5
sec. The components of the feature position error tend
asymptotically to a small neighborhood of zero ( 2
and -3 pixels, respectively).
ICINCO 2005 - ROBOTICS AND AUTOMATION
364

Figure 3: Feature position error trajectory in the image
plane for controller (9).
Figure 4: Feature position error trajectory in the image
plane for controller (10).
Finally the experimental results for the controller
τ = f (K
p
, ˜u, ˜v) − K
v
˙
q + g(q) (10)
where
f (K
p
, ˜u, ˜v) =
f
1
(K
p
, ˜u, ˜v)
.
.
.
f
n
(K
p
, ˜u, ˜v)
f
i
(K
p
, ˜u, ˜v) =
f
p
(tanh)
i
if |f
p
(sinh)
i
| ≥ σ
+
i
f
p
(sinh)
i
if |f
p
(sinh)
i
| < σ
+
i
for all i = 1, 2, ..., n and
f
p
(tanh)
1
.
.
.
f
p
(tanh)
n
= J
T
(q)K
p
R(θ) tanh Λ
˜u
˜v
f
p
(sinh)
1
.
.
.
f
p
(sinh)
n
= J
T
(q)K
p
R(θ) sinh Λ
˜u
˜v
are shown in Figure 4. The gains were se-
lected as K
p
= diag{25.85, 3.93} [Nm/pixels
2
],
K
v
= diag{0.17, 0.018} [Nm-sec/degrees] respec-
tively and Λ = diag{0.1, 0.1}. The transient re-
sponse was around 0.75 sec. The components of the
feature position error tend asymptotically to -1 and -2
pixels, respectively.
To compare the experimental results obtained for
the three controllers we use the L
2
norm (Khalil,
2002) of the feature position error. For the controller
(8) L
2
[˜u ˜v]
T
= 3.50 [pixels], then for the controller
(9) L
2
[˜u ˜v]
T
= 3.99 [pixels], finally for the controller
(10) L
2
[˜u ˜v]
T
= 2.47 [pixels]. Therefore the smallest
L
2
norm corresponds to the controller (10), then this
controller presents the best steady state performance.
6 CONCLUSIONS
This paper has introduced a new family of position
control algorithms for robot manipulators. It is sup-
ported by a rigorous stability analysis, the theoretical
results establish conditions for ensuring global reg-
ulation. The simple PD controller can be a particu-
lar member of this new scheme when its proportional
gain is a diagonal matrix. Applications for Visual Ser-
voing have been shown.
For stability purposes, the tuning procedure for the
new scheme is sufficient to select a proportional gain
as diagonal matrix and derivative gain as symmetric
positive definite matrix in order to ensure global as-
ymptotic stability.
REFERENCES
A. Loria, E. Lefeber, . H. N. (2002). Global asymptotic
stability of robot manipulators with linear pid and pi
2
d
control. In SACTA.
Armstrong-Ho
´
elouvry, B. (1991). Control of Machines with
Friction. Kluwer Academic Publishers, Boston, 1st
edition.
B. Armstrong-Ho
´
elouvry, D. Neevel, . T. K. (1999). New
results in npid control: Tracking, integral control, fric-
tion compensation and experimental results. In Pro-
ceedings of the 1999 IEEE International Conference
on Robotics and Automation.
C. Canudas, B. Siciliano, . G. B. (1996). Theory of Robot
Control. Springer, Great Britain, 1st edition.
Craig, J. J. (1989). Introduction to Robotics: Mechanics and
Control. Addison–Wesley, Massachusetts, 1st edition.
F. L. Lewis, C. T. Abdallah, . D. M. D. (1993). Control
of Robot Manipulators. MacMillan Publishing Com-
pany, N.Y., 1st edition.
A NEW FAMILY OF CONTROLLERS FOR POSITION CONTROL OF ROBOT MANIPULATORS
365

J. Alvarez, R. Kelly, . I. C. (2003). Semiglobal stability of
saturated linear pid control for robot manipulators. In
Automatica.
Kelly, F. R. . R. (1997). Experimental evaluation of identi-
fication schemes on a direct drive robot. In Robotica.
Cambridge University Press.
Kelly, R. (1995). A tuning procedure for stable pid control
of robot manipulators. In Robotica. Cambridge Uni-
versity Press.
Kelly, R. (1999). Regulation of manipulators in generic task
space: An energy shaping plus damping injection ap-
proach. In IEEE Trans. on Robotics and Automation.
IEEE.
Khalil, H. K. (2002). Nonlinear Systems. Prentice–Hall,
N.J., 3rd edition.
Koditschek, D. (1984). Natural motion for robot arms. In
Proceedings of the 1984 IEEE Conf. on Decision and
Control.
L. Sciavicco, . B. S. (1996). Modeling and Control of Robot
Manipulators. The McGraw–Hill Companies, Inc.,
London, 2nd edition.
M. Takegaki, . S. A. (1981). A new feedback method for dy-
namic control of manipulators. In J. Dyn. Syst. Meas.
Control Trans. ASME.
O. Khatib, J. J. Craig, . T. L.-P. (1989). The Robotics Review
1. M.I.T. Press, Massachusetts, 1st edition.
R. Kelly, . R. C. (1996). A class of nonlinear pd–type con-
trollers for robot manipulators. In Journal of Robotic
Systems.
S. Arimoto, . F. M. (1986). Stability and robustness of pd
feedback control with gravity compensation for ro-
bot manipulator. In Robotics: Theory and Practice.
ASME winter annual meeting.
Seraji, H. (1998). A new class of nonlinear pid controllers
with robotic applications. In Journal of Robotic Sys-
tems.
V. Santiba
˜
nez, R. Kelly, . F. R. (1998). A new set–point
controller with bounded torques for robot manipula-
tors. In IEEE Transactions on Industrial Electronics.
IEEE.
Vidyasagar, M. W. S. . M. (1989). Robot Dynamics and
Control. John Wiley & Sons, N.Y., 1st edition.
Y. Xu, J. M. Hollerbach, . D. M. (1995). A nonlinear pd
controller for force and contact transient control. In
IEEE Control Systems. IEEE.
ICINCO 2005 - ROBOTICS AND AUTOMATION
366
