MULTI-BAND GPS SIGNAL TRACKING IN A HIGH DYNAMIC
MANEUVERING SITUATION
Stanislas Boutoille, Serge Reboul, Mohammed Benjelloun
Laboratoire d’Analyse des Syst
`
emes du Littoral (EA 2600)
50 Rue Ferdinand Buisson, B.P 699, 62228, Calais Cedex, France
Keywords:
GPS, detection, information fusion.
Abstract:
In a GPS receiver, the goal of the signal tracking is to synchronize local generated code and carrier with the
received signal. After a step of acquisition, the receiver tracks the shifting of the local code provoked by
the movements of the receiver and satellites. In the future evolution of the GPS, the system will have several
carrier frequencies, then it will be possible to have several tracking systems working simultaneously for a same
satellite. We present in this article a detection method for the tracking of the future multi-band GPS signal.
This method is applied to the localization of a vehicle which makes high dynamic maneuver. We define
a MAP detection criterion to fuse the shifts discriminator detection achieved on multi carrier frequencies.
This criterion is defined in the case when shifts are not necessary simultaneous and when there is a lack of
information on one frequency provoked by the unlocking of the code tracking on one of the carrier. Indeed,
there is a difference between the instants of shifts on the different carrier frequencies. This difference is due
to the effect of ionospheric propagation. The experimentations achieved on synthetic GPS signals show the
advantages of the method compared to the classical algorithm.
1 INTRODUCTION
In the future GPS system, the civil code will be avail-
able on several carrier frequencies. This is the case
for NAVSTAR with the three frequencies L1, L2 and
L5 and for Galileo. The CDMA codes on these car-
riers will have different frequencies and shapes (BOC
modulation). In this context it is interesting to per-
form the tracking of the codes simultaneously in the
receiver on the different carriers. Indeed, we can
combine the tracking information and then increase
the accuracy and robustness of the tracking process.
The synchronisation between the received code and
the generated code is realized by the measurement of
the maximum of the correlation. It is the step of ac-
quisition. Each satellite has a different ranging code
and so we can deduce the visible satellites and the
distance between the satellite and the receiver. After
this phase, the receiver tracks the shifting of the local
code provoked by the movements of the receiver and
satellites. In the GPS future evolution, the system will
have several carrier frequencies, then it will be possi-
ble to have several tracking systems working simulta-
neously for a single satellite. We present in this article
a detection method for tracking fusion applied to the
future multi carrier frequencies signal GPS . The gen-
eralized likelihood ratio (GLR) (Willsky and Jones,
1976) is a statistical test based on the likelihood ratio.
It was first applied to the detection of abrupt changes
on a signal coming from a linear system. We found
in the literature two different approaches of the detec-
tion fusion: the centralized detection and the distrib-
uted one. The distributed detection, very largely stud-
ied by (Rao, 2001) and (Varshney, 1996), considers
the detection at the level of each sensor and then car-
ries out a global decision by combination of the local
decisions. The difficulties in this case lie in the def-
inition of the thresholds at the level of each local de-
tector. Most of the works on this subject are based on
criterion to be optimized such as Bayes or Neyman-
Pearson. Actually a great number of papers deals with
the problem of correlated decisions in the fusion case
(Chen and Ansari, 1998). The centralized detection
system considers all the measurements to perform the
decision. This system offers the best performances
but the quantity of information to be processed by the
fusion system can quickly become significant. One of
the drawbacks of this approach is its sensitivity to the
synchronisation of the data. Various works concern
the weighting of the distributions in order to favour
258
Boutoille S., Reboul S. and Benjelloun M. (2005).
MULTI-BAND GPS SIGNAL TRACKING IN A HIGH DYNAMIC MANEUVERING SITUATION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 258-263
DOI: 10.5220/0001174902580263
Copyright
c
 SciTePress

some measurements compared to others during fu-
sion. The logarithm opinion pool (Benediktsson and
Sveinsson, 1997) is derived from the joint probabil-
ities using the Bayes’ rule. The best difficulty asso-
ciated to the use of this kind of method is the weight
selection. Different interferences can disturb the GPS
signal measurements and then improve the detection
during the tracking process. Indeed, the received sig-
nal can be unlocked and then the tracking process can
not perform any more. This happens more frequently
with codes of high frequency. The goal of this work
is to realize the detection in the tracking system on
different frequencies in order to overcome these per-
turbations and then to increase accuracy and robust-
ness. We propose a weighted hybrid fusion method
inspired of the logarithmic opinion pool method. The
introduction of weight in the hybrid fusion system,
proposed in (Boutoille et al., 2004), increases the ro-
bustness in presence of unlocking. Hybridizing cen-
tralized and distributed fusion system permits to deal
with unsynchronized signal on the carriers. Indeed,
the ionosphere crossing causes a group velocity de-
lay of the waves according to frequencies (M. Grewal
and Andrews, 2001). The paper is organized as fol-
lowing. Section 2 describes the GPS signal model.
The system of weigthed fusion is described in section
3 and the fusion method in section 4. In section 5 we
present numerical experimentations on synthetic GPS
signals.
2 MODEL OF GPS SIGNAL
2.1 Statistical model
The incoming GPS signal is demodulated and cor-
related with respectively a carrier and a code gener-
ated by the receiver. Let consider the expression of
the in-phase and quadrature components after corre-
lation and demodulation for each time of samples t
k
(Dierendonck et al., 1992):
I
k
=
p
2C/N
0
T R
f
(τ
k
) cos(φ
k
) + n
ik
(1)
Q
k
=
p
2C/N
0
T R
f
(τ
k
) sin(φ
k
) + n
q k
(2)
With :
T = predetection bandwith where the correla-
tion is done,
φ
k
= residual phase tracking error at time t
k
,
τ
k
= is the shift between the local and the re-
ceived code CDMA ,
n
k
= the in-phase and quadraphase noise sam-
ples,
R
f
= correlation between filtered signal and the
non-filtered code generated,
C/N
0
= signal-to-noise ratio normalized to a 1
Hz bandwith.
In the non-coherent case, the mean of the early-
minus-late discriminator is given by :
E [D
τ
k
] =
¯
I
2
E
+
¯
Q
2
E
−
¯
I
2
L
−
¯
Q
2
L
(3)
Where I
E
and Q
E
are the in-phase and quadrature
component, correlated with a code which is generated
slightly early. I
L
and Q
L
are the same components
correlated with a code slightly late. We can calculate
the discriminator’s statistical parameters. So for the
mean :
E [D
τ
k
] = 2C/N
0
T

R
2
f
(τ
k
−
T
c
2
) − R
2
f
(τ
k
+
T
c
2
)

(4)
And the variance :
σ
2
D
τ
k
= 8+8 C/N
0
T

R
2
f
(τ
k
−
T
c
2
) + R
2
f
(τ
k
+
T
c
2
)

(5)
The code’s properties make that the delay is carac-
terized by changes of stationnarities on the dicrimi-
nator measurements. Indeed, when the delay exceeds
the value of the sampling period, there is a change
in the mean and the variance. It is from the detec-
tion of this change that the code locally generated is
readjusted with the received code. After a step of ac-
quisition,the value of the delay τ
k
in the expression
of the correlation is zero. This step of acquisition is
followed by a step of tracking where the local code
is shifted to stay locked with the receiving code. In
this step we try to keep the discriminator value close
to zero.
2.2 Problem position
The statistical parameters and the detection quality,
are function of the correlation measurement R
f
. The
expression of the correlation R
f
changes with the fre-
quency of the code CDMA. Therefore, for a fixed τ
k
,
the correlation’s value is different. A higher code fre-
quency will have a narrower peak of correlation and
will allow a better detection of the shifts caused by
the delay. Indeed, the correlation’s evolution for fixed
value of τ increases with the code frequency. Unfor-
tunately, the sensitiveness of the code to unlock in-
creases also with the code frequency. In the case of
higher frequency, the tracking is more accurated but
less robust especially when the relatives speeds be-
tween the receiver and the satellites are high. The
goal of this work is to fuse the information coming
from the frequencies of a multi carrier GPS receiver.
In this context, we want to improve accuracy and ro-
bustness of the tracking for codes with different fre-
quencies.
MULTI-BAND GPS SIGNAL TRACKING IN A HIGH DYNAMIC MANEUVERING SITUATION
259

3 LOGARITHM OPINION POOL
The posterior probability to have a sequence of rup-
tures r
in a signal y is written (Reboul and Benjelloun,
2004):
sup
{r
, θ}
P
r
(R
= r/Y = y; θ) (6)
We consider two hypothesis, H
1
and H
0
respec-
tively for the presence and the absence of change on
a signal. We can then write the following rule of de-
cision:
sup
{r
1
}
P
r
(R
1
= r
1
/Y
= y; θ
1
) (7)
<
H
0
>
H
1
sup
{r
0
}
P
r
(R
0
= r
0
/Y
= y; θ
0
)
with r
1
and r
0
, the changes sequences respectively
associated to the hypothesis H
1
and H
0
. The para-
meters θ
1
and θ
0
corresponding respectively to the
sequences r
1
and r
0
are assumed to be known c.f.
equations(6,7).
In the case of J signals, the information combina-
tion with the logarithm opinion pool method, gives
the following test of hypothesis:
sup
{r
1
}
(
Q
J
j=1
P
r
(R
1
= r
1
/Y
j
= y
j
; θ
j
1
)
β
j
) (8)
<
H
0
>
H
1
sup
{r
0
}
(
Q
J
j=1
P
r
(R
0
= r
0
/Y
j
= y
j
; θ
j
0
)
β
j
),
where β
j
is the weighted coefficient and y
j
the signal
j. With this formulation we can define different tests
for different values of β
j
. For example if one signal
is unlocked his associated value β
j
is set to zero.
4 SYSTEM OF WEIGHTED
FUSION
4.1 Centralized fusion
Let define with the expression 8, the centralised fu-
sion test. The Bayes’ theorem gives us:
sup
{r
1
}
{
Q
J
j=1
(h (y
j
/r
1
; θ
1
j
) f(θ
1
j
) π
j
(r
1
))
β
j
}
<
H
0
>
H
1
(9)
sup
{r
0
}
{
Q
J
j=1
(h (y
j
/r
0
; θ
0
j
) f(θ
0
j
) π
j
(r
0
))
β
j
}
where:
π
j
(r
i
) = is the prior law of the change config-
uration r
i
is the change configuration associated
to the hypothesis H
i
for the signal j, i ǫ {0, 1},
f(θ
j
) = is the prior law for the statistical para-
meters. It is supposed to be an uniform law on
all the values of θ
j
.
By taking the logarithm of the preceding expres-
sion and let λ
j
=
π
j
(r
0
)
π
j
(r
1
)
, we can then write the deci-
sion criterion:
sup
{r
1
,r
0
}
{
P
J
j=1
β
j
. (ln (h
j
(y
j
/r
1
; θ
1
j
))−
ln (h
j
(y
j
/r
0
; θ
0
j
)))}
<
H
0
>
H
1
P
J
j=1
β
j
. ln(λ
j
) (10)
where r
i
the change point’s configuration associ-
ated to the hypothesis H
i
is the same for the two sig-
nals.
4.2 Decentralized fusion
In the decentralized case, we consider different con-
figurations of change for each signal. The estimate
of these configurations is done independently on each
signal. We have:
P
J
j=1
{sup
{r
1
j
,r
0
j
}
(β
j
. (ln (h
j
(y
j
/r
1
j
; θ
1
j
))−
ln (h
j
(y
j
/r
0
j
; θ
0
j
))))}
<
H
0
>
H
1
P
J
j=1
β
j
. ln(λ
j
)(11)
This fusion’s system is adapted in the case where
the changes are not synchronized.
4.3 Hybrid fusion
In the hybrid fusion method we proposed, we com-
bine the decisions of the centralized fusion and de-
centralized fusion systems (Boutoille et al., 2004).
The thresholds of the centralized and distributed fu-
sion methods and the rule of combination are chosen
to maximize the Neyman Pearson criterion. To de-
fine the decision rule of each fusion method, we use
an optimization element by element. Then we search
the decision rules that maximize the Lagrangian L
(Varshney, 1996), define in this case as :
L = P
D
− (
J
Y
j=1
λ
β
j
j
)(P
F
− α) (12)
Let consider here the case of N local detector and
a global fusion detector that combines the local deci-
sions. u
i
= j is the decision of the hypothesis H
j
by
the detector i. u
0
= j is the global decision of the
fusion system. We have :
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
260

P
f
= P (u
0
= 1/H
0
) =
X
u
P (u
0
= 1/u)P (u/H
0
)
(13)
where u is all the possible combinations of detec-
tions. Then we have :
L = P
D
− (
Q
J
j=1
λ
β
j
j
)(P
F
− α) = (14)
P
D
− (
Q
J
j=1
λ
β
j
j
)P
F
+ α(
Q
J
j=1
λ
β
j
j
)
with :
L =
P
N
u=1
P (u
0
= 1/u)P (u/H
1
)− (15)
(
Q
J
j=1
λ
β
j
j
)((
P
u
P (u
0
= 1/u)P (u/H
0
)) − α)
and :
L = (
Q
J
j=1
λ
β
j
j
)α +
P
u
P (u
0
= 1/u)[P (u/H
1
)
−(
Q
J
j=1
λ
β
j
j
)P (u/H
0
)] (16)
We use an optimization elements by elements, and
we have:
L = (
J
j=1
λ
β
j
j
)α +
u
k
P (u
0
= 1/u
k
= 0, u
k
).
[P (u
k
= 0, u
k
/H
1
) − (
J
j=1
λ
β
j
j
)P (u
k
= 0, u
k
/H
0
)]
+
u
k
P (u
0
= 1/u
k
= 1, u
k
).[P (u
k
= 1, u
k
/H
1
)
−(
J
j=1
λ
β
j
j
)P (u
k
= 1, u
k
/H
0
)] (17)
where, u
k
= (u
1
, · · · , u
k−1
, u
k+1
, · · · u
N
)
T
. In
our case the measurements are correlated then we
have :
P (u
1
, u
2
, · · · , u
N
/H
1
) (18)
= P (u
1
/H
1
)
Q
N
j=2
P (u
j
/u
1
, u
2
, · · · , u
j−1
, H
1
)
with N the number of sensors.
Therefore :
P (u
k
= 0, u
k
/H
1
)
= P (u
1
/H
1
)
Q
N
j=2,
j6=k
[P (u
j
/u
1
, · · · , u
j−1
, H
1
)
.P (u
k
= 0/u
1
, · · · , u
k−1
H
1
)] (19)
Let :
P
′
(u
k
/H
1
)
= P (u
1
/H
1
)
Q
N
j=2,
j6=k
P (u
j
/u
1
, · · · , u
j−1
, H
1
)
6= P (u
k
/H
1
) (20)
Since u
k
does not depend on H
i
, we can write :
P (u
k
= 1/u
1
, · · · , u
k−1
, H
i
) (21)
=
R
y
k
P (u
k
= 1/u
1
, · · · , u
k−1
, y
k
)P (y
k
/H
i
)dy
k
We can write :
L = C
k
+
R
y
k
P (u
k
= 1/u
1
, · · · , u
k−1
, y
k
)[C
k
1
P (y
k
/H
1
)
−(
Q
J
j=1
λ
β
j
j
)C
k
0
P (y
k
/H
0
)]dy
k
(22)
with :
C
k
= (
Q
J
j=1
λ
β
j
j
)α
+
P
u
k
P (u
0
= 1/u
k
= 0, u
k
)[P
′
(u
k
/H
1
)
−(
Q
J
j=1
λ
β
j
j
)P
′
(u
k
/H
0
)] (23)
and :
C
k
i
=
P
u
k
[P (u
0
= 1/u
k
= 1, u
k
)
−P (u
0
= 1/u
k
= 0, u
k
)]P
′
(u
k
/H
1
) (24)
C
k
is independent of the decision rule associated to
the detector k, then L is maximum when the integral
of the expression 22 is maximum. We have :
P (u
k
= 1/u
1
, · · · , u
k−1
, y
k
) = 0,if (25)
C
k
1
P (y
k
/H
1
) − (
Q
J
j=1
λ
β
j
j
)C
k
0
P (y
k
/H
0
) < 0
and :
P (u
k
= 1/u
1
, · · · , u
k−1
, y
k
) = 1,if (26)
C
k
1
P (y
k
/H
1
) − (
Q
J
j=1
λ
β
j
j
)C
k
0
P (y
k
/H
0
) > 0
The decision rule of the detector k is given by:
P (y
k
/H
1
)
P (y
k
/H
0
)
<
H
0
>
H
1
λ
′
k
(27)
With :
λ
′
k
= (
J
Y
j=1
λ
β
j
j
)
C
k
0
C
k
1
(28)
We consider here the case of our application, two
detectors (the decisions are coming from the two fu-
sion methods) and the fusion rules AND and OR. Let
λ
′
1
be the threshold value for the centralized fusion
and λ
′
2
the threshold value for the distributed fusion
criterion :
λ
′
1
= (
J
Y
j=1
λ
β
j
j
)
P f
2
P d
2
(29)
MULTI-BAND GPS SIGNAL TRACKING IN A HIGH DYNAMIC MANEUVERING SITUATION
261

and :
λ
′
2
= (
J
Y
j=1
λ
β
j
j
)
P f
1
1
P d
1
1
(30)
Where P d
1
1
is the probability to detect with the cen-
tralized fusion method when we have detected with
the decentralized fusion method. For hybrid fusion
AND we have:
λ
′
1
P f
1
1
P d
1
1
= λ
′
2
P f
2
P d
2
(31)
For the OR hybrid fusion:
λ
′
1
1 − P f
1
1
1 − P d
1
1
= λ
′
2
1 − P f
2
1 − P d
2
(32)
We observe in our experimentations that we have
better performances for the AND fusion rule than for
the OR fusion rule. We will use the AND fusion rule
for the experimentations.
5 APPLICATION TO GPS SIGNAL
TRACKING
We present experimentations in order to measure the
performances of the method in the presence of un-
locks on the signals. The code on L5 has a higher
frequency than on L1. This frequency will then be
brought to unlock more easily
5.1 Experimentations
In these simulations, we realize a code tracking in
a realistic dynamic context. We consider positions
of a dynamic receiver, an 8 satellites constellation,
and a mean HDOP (Horizontal Dilution Of Precision)
of 1 during the experimentation. The receiver has a
100 m/s speed with a trajectory that changes during
2 s. We provide measurement every ms. The sam-
pling rate is fixed at 20.46 MHz and the frequency of
the L1 code is 1.023 MHz against 10.23MHz for L5.
The power of the signals is fixed for simulation at 40
dB.Hz for each satellite. When an unlocking occurs
during the tracking process, the value of correlation is
close to 0 and we have E [D
τ
k
] = 0 and σ
2
d
τ
k
= 8 for
the statisticals parameters of the discriminator. In or-
der to define the weighted coefficients, we realize first
a test which indicates the presence of unlocking. This
test is carried out independently on the singles fre-
quencies measurements and the thresholds are fixed
to detect the unlocking with probability one. In this
case, we can define the values of the weighting coef-
ficients β
j
. We affect the value β
1
= 1 and β
2
= 0
when we detect an unlocking for L5 and the tracking
is only performed on L1. In the same way, we affect
−20 −15 −10 −5 0 5 10 15 20
−20
−15
−10
−5
0
5
10
15
20
north error (m)
east error (m)
L5
L1
Figure 1: L1 and L5 error measurements.
−40 −20 0 20 40 60 80
−10
−5
0
5
10
15
20
25
30
Y trajectory (m)
X trajectory (m)
L5
True trajectory
L1
Figure 2: L1 and L5 trajectory measurements.
the value β
1
= 0 and β
2
= 1 when L1 is unlocked.
For all the other cases, we fused the tracking of the
two carriers by affecting β1 = 0.5 and β2 = 0.5.
5.2 Results
We show figures 1 and 3 the position errors on X and
Y for the receiver trajectory defined on figures 2 and
4. On figure 1, we display in blue the results obtained
for the L5 code tracking and in red the results obtained
for the L1 code tracking. The estimate trajectories
displayed on figures 2 and 4 are obtained after filter-
ing the GPS data with a navigation Kalman filter. We
can see in this experimentation that the measurements
on L5 give better performances than L1. But during
the experimentation three satellites get unlocks on L5
and all the satellites stay locked on L1.
On figure 3, we display in blue the results obtained
for the classical hybrid fusion tracking code and in
red the results obtained for the weighted hybrid fu-
sion. This experimentation shows that the tracking
fusion method gives better performances than the sin-
gle tracking process. The weighted hybrid fusion of-
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
262

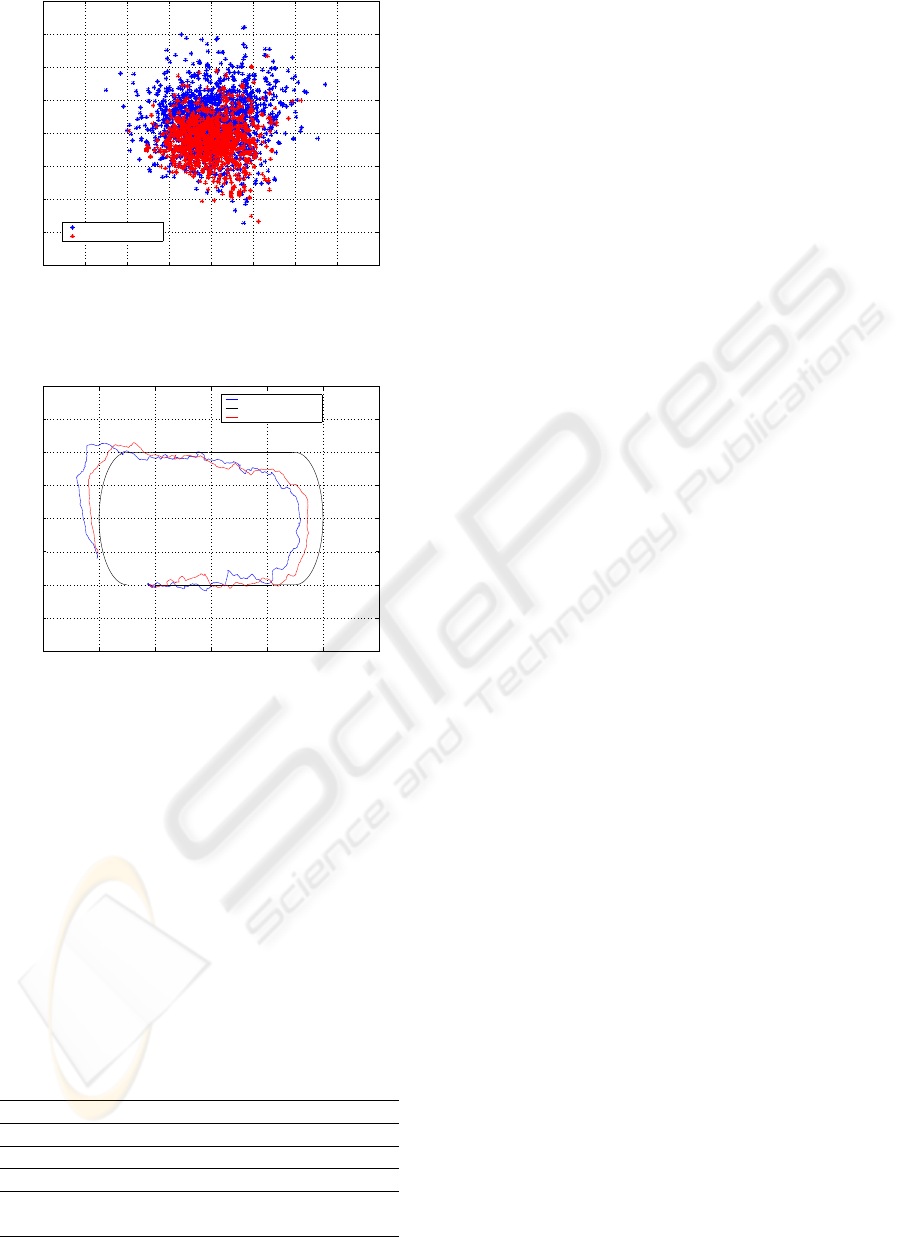
−20 −15 −10 −5 0 5 10 15 20
−20
−15
−10
−5
0
5
10
15
20
north error (m)
east error (m)
Hybrid fusion
Weighted hybrid fusion
Figure 3: Hybrid fusion error measurements.
−40 −20 0 20 40 60 80
−10
−5
0
5
10
15
20
25
30
Y trajectory (m)
X trajectory (m)
Hybrid fusion
True trajectory
Weighted hybrid fusion
Figure 4: Hybrid fusion trajectory measurements.
fers best results than classical hybrid fusion and there
is one satellite unlocked for the classical hybrid fu-
sion while all the satellites are locked for weighted
hybrid fusion. We report TABLE 1 measurements of
the root mean squared error in meters on X and Y
for each case as well as a measurement of the eccen-
tricity. The eccentricity is the distances between the
mean position and the real position. We can notice
that the proposed method has better performances for
this criterion.
Table 1: Root mean squared error in meters.
X Y Eccentricity
L1 6.80 4.53 5.08
L5 4.43 4.55 1.36
Hybrid fusion 3.67 4.25 1.72
Weighted Hybrid
fusion 2.88 3.15 1.04
6 CONCLUSION
The goal of this work is to track different GPS car-
rier frequencies in a high dynamic situation. We pro-
pose a weighted hybrid fusion method inspired of
the logarithmic opinion pool method. The introduc-
tion of weight in the hybrid fusion system increases
the robustness in presence of unlocks. Furthermore,
hybridizing centralized and distributed fusion system
will permit to deal with unsynchronized signal on the
carriers. We show in the experimentations on syn-
thetic GPS L1 and L5 signals, that our method of fu-
sion increases tracking robustness and accuracy and
avoided the unlocking for the higher frequency code.
The perspectives of this work are about the general-
ization of the method for more than two carrier fre-
quencies and its application to the future signals of
GALILEO.
REFERENCES
Benediktsson, J. A. and Sveinsson, J. R. (1997). Hybrid
consensus theoric classification. IEEE Transactions
on Geoscience and Remote sensing, 35(4):833–843.
Boutoille, S., Reboul, S., and Benjelloun, M.(2004). Fusion
of detections in a multi-carrier gps receiver. In Pro-
ceedings of the Seventh International Conference on
Information Fusion, pages 85–90, Stockholm, Swe-
den.
Chen, J. and Ansari, N. (1998). Adaptative fusion of cor-
related loacal decisions. IEEE Transactions On Sys-
tems, Man., And Cybernetics - Part C : Applications
And Reviews, 28(2):276–281.
Dierendonck, A. V., Fenton, P., and Ford, T. (1992). Theory
and performance of narrow correlator spacing in a gps
receiver. journal of the Institute of Navigation, USA,
39(3):265–283.
M. Grewal, L. W. and Andrews, A. (2001). Global Posi-
tioning System, Inertial Navigation and Integration.
Wiley Interscience, New Jersey.
Rao, N. (2001). On fusers that perfor better than best sensor.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 23(8):904–909.
Reboul, S. and Benjelloun, M. (2004). Joint segmentation
of a set of piecewise stationary processes. In IEEE
International Conference on Computal Cybernetics,
pages 191–195, Austria.
Varshney, P. K. (1996). Distributed detection and data fu-
sion. Springer.
Willsky, A. and Jones, H. (1976). A generalized likeli-
hood ratio approach to the detection and estimation
of jumps in linear systems. IEEE Transactions on Au-
tomatic Control, 21:108–112.
MULTI-BAND GPS SIGNAL TRACKING IN A HIGH DYNAMIC MANEUVERING SITUATION
263