MUSICAL INSTRUMENT ESTIMATION FOR POLYPHONY
USING AUTOCORRELATION FUNCTIONS
Yoshiaki Tadokoro
Dept. of Information and Computer Sciences, Toyohashi University of Technology,Toyoahashi,441-8580 Japan
Koji Tanishita
Dept. of Information and Computer Sciences, Toyohashi University of Technology,Toyoahashi,441-8580 Japan
Keywords: musical instrument estimation, polyphony, autocorrelation function.
Abstract: This paper proposes a new musical instrument estimation of polyphony using autocorrelation
functions. We notice that each musical instrument has each autocorrelation function. Polyphony
can be separated into each monophony using comb filters ( ). We can obtain the
autocorrelation functions for the outputs of comb filters from the autocorrelation functions of the
monophony. By the pattern patching between the autocorrelation functions for the output signals
of the comb filters and ones calculated from monophony of each instrument, we can estimate the
musical instruments for polyphony.
N
zzH
−
−= 1)(
1 INTRODUCTION
Musical transcription is necessary in the musicology
field, musical retrieval and also a significant
problem in machine perception (Roads, 1985),
(Sterian and Wakefield, 2000), (Pollasri, 2002). In
the transcription, the pitch estimation is most
important and many studies have been done (Roads,
1996), (Tadokoro el al, 2001, 2002, 2003),. We also
proposed a unique method of the pitch estimation
that is based on the elimination of the pitch and its
harmonic components using the cascade or parallel
connections of the comb filters (Tadokoro el al,
2001, 2002, 2003). On the other hand, there are not
many studies for the instrument estimation(Brown
and cooke, 1994), (Abe and Ando, 1996), (Zhang,
2001), (Lee and Chun, 2002), (Krishan and
Steenivas, 2004), (Jincahita, 2004), although the
instrument estimation is also necessary in the
transcription. Most of old studies are for
monophony and based on the spectrum analysis of a
musical sound. In the recent studies, the new
technologies such as neural network, fuzzy logic
(Zhang, 2001), hidden morkov model (Lee and Chun,
2002) and independent subspace analysis (Jincahita,
2004).
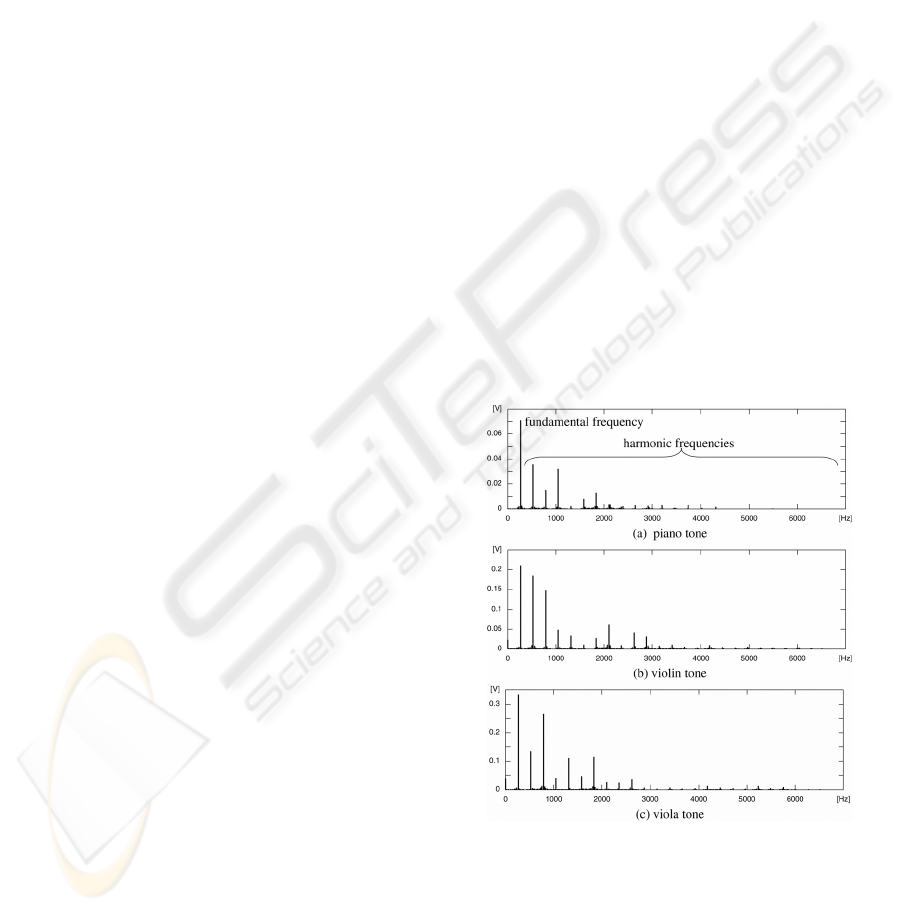
Figure 1: Spectra of tones, (a)piano, (b)violin and
(c)viola
4
C
143
Tadokoro Y. and Tanishita K. (2005).
MUSICAL INSTRUMENT ESTIMATION FOR POLYPHONY USING AUTOCORRELATION FUNCTIONS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 143-148
DOI: 10.5220/0001175001430148
Copyright
c
SciTePress

Figure 2: STFT result of piano tone
4
C
The spectrum of each musical instrument has
different frequency components as shown in Fig.1.
Therefore the instrument estimation based on the
spectrum analysis is reasonable. But there are some
problems in the instrument estimation based on the
spectrum analysis. One of them is that the spectrum
for the signal just after the instrument is played is
unstable. Figure 2 shows the result of the short-time
Fourier transform (STFT) of piano tone
4
C ( of
octave 4). In the range from 0.0 to 0.4 s, the each
harmonic component is changing irregularly. But,
we must estimate the instrument in a short duration
signal like about 100ms, because a sixteenth note is
125 ms at the tempo of a quarter note =120.
Another is that tones in lower octaves have lower
fundamental frequencies and to separate polyphony
into each monophony and obtain these spectra by the
FFT method, we must use a longer signal duration
necessarily. For an example, to distinguish two tones
of
2
and
#2#2 C
,
we must use at least a signal duration of 257 ms,
because the frequency difference between these two
tones is 3.89 Hz. That is, the method based on the
DFT must use the longer signal duration to obtain a
higher frequency resolution. On the other hand, the
method based on the parametric model such as the
linear prediction method (LPM) can calculate the
spectrum from a smaller data. Then we considered
the instrument estimation for monophony musical
sound using the LPM that could be applied to the
sounds of the shorter duration like about 50 ms
(Tadokoro et al, 2004). But, the LPM method has
the problem that it has many computations and the
prediction coefficients are sensitive to the change of
a signal waveform.
C
C )41.65(
2
Hzf
c
= )30.69
0244872
–1
0
1
clarinet
horn
alt–sax
viola
violin
auto–correlation R(k)
k
unstable
Figure 3: Autocorrelation functions of tones for
five instruments
)(kR
4
C
Table 1: Accumulated differences between the
autocorrelation functions (
) of two
instruments
)(),( kRkR
qp
0violin
16.170viola
19.7417.190alt-sax
7.8222.7123.200horn
19.5612.5019.2524.910clarinet
violinviolaalt-saxhornclarinet
C
4
0violin
16.170viola
19.7417.190alt-sax
7.8222.7123.200horn
19.5612.5019.2524.910clarinet
violinviolaalt-saxhornclarinet
C
4
In this paper, we consider the instrument
estimation using each autocorrelation function for
each instrument. The proposed method has a smaller
computation than the LPM, because the p-order
LPM must use
pp
×
autocorrelation functions and
solve the Yule-Walker equation. Furthermore, we
consider the instrument estimation for polyphony
musical sound that may be suitable to the pitch
( HzfC =
estimation method using comb filters that we
proposed.
We assume that the polyphony is composed of
two different tones of which pitches have already
estimated by the pitch estimation method. And the
input sounds are real sounds of five instruments
(clarinet, horn, alto-sax, viola and violin) and are in
octave 3 to 5. These database (RWC music database)
are made by the Real World Computing Partnership
in Japan. The sampling frequency is
.
The playing method is moderate but not piano or
forte.
kHzf
s
1.44=
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
144

Figure 4: Autocorrelation functions of some instrument
makers
Table 2: Accumulated differences between auto-
correlations functions of some instrument makers
Table 3: Instrument estimation results for tone
4
C
982
3
3
000violin
09700viola
0010000alt-sax
0001000horn
00097clarinet
violinviolaalt-saxhornclarinet
98000violin
09700viola
0010000alt-sax
0001000horn
00097clarinet
violinviolaalt-saxhornclarinet
2
3
3
2 INSTRUMENT ESTIMATION
FOR MONOPHONY USING
AUTOCORRELATIO
FUNCTIONS
2.1 Autocorrelation Function of
Monophony
We calculate the autocorrelation function of a signal
by )(nx
∑
−
=
+=
1
0
)()(
1
)(
M
n
knxnx
M
kR (1)
Figure 3 shows the autocorrelation functions
of
tones for five instruments calculated by using
)(kR
4
the signals of 50 ms duration in the beginning part of
the sounds. Table 1 represents the accumulated
differences of
between two instruments
showing in Eq.(2)
C
)(kR
∑
=
−=−
r
k
qp
kRkRqpAD
0
)()()( (2)
From these results, we can realize that we can
estimate the instruments by the autocorrelation
functions
. )(kR
0 244872
–1
0
1
k
auto–correlation Rxx(k)
SELMER
YAMAHA
GEMEINHA
4
C
clarinet( )
0 244872
–1
0
1
k
auto–correlation Rxx(k)
SELMER
YAMAHA
GEMEINHA
4
C
clarinet( )
4
C
clarinet( )
0 244872
–1
0
1
k
auto–correlation Rxx(k)
J.F.PRESSENDA
CARCASSI
FIUMEBIANCA
violin( )
4
C
0 244872
–1
0
1
k
auto–correlation Rxx(k)
J.F.PRESSENDA
CARCASSI
FIUMEBIANCA
violin( )
4
C
violin( )
4
C
0 244872
–1
0
1
k
auto–correlation Rxx(k)
ALEXANDER
KNOPF
YAMAHA
4
C
horn( )
0 244872
–1
0
1
k
auto–correlation Rxx(k)
ALEXANDER
KNOPF
YAMAHA
4
C
horn( )
4
C
horn( )
sound
est.
sound
est.
But we have one problem that the autocorrelation
functions for instruments are different depending on
the instrument makers. Figure 4 shows the
autocorrelation functions for some instruments of
some instrument makers. Table 2 represents the
accumulated differences
between these
autocorrelation functions. From these results, we
must prepare the templates for each instrument
maker.
)( qpAD −
0viol.3
34.80viol.2
23.99.70viol.1
27.212.74.10hor.3
34.111.455.538.20hor.2
13.88.4911.914.5140hor.1
3929.824.323.523.427.40clar.3
38.427.721.521.130.926.511.60clar.2
42.329.119.618.532.328.610.514.80clar.1
viol.3viol.2viol.1hor.3hor.2hor.1clar.3clar.2clar.1
0viol.3
34.80viol.2
23.99.70viol.1
27.212.74.10hor.3
34.111.455.538.20hor.2
13.88.4911.914.5140hor.1
3929.824.323.523.427.40clar.3
38.427.721.521.130.926.511.60clar.2
42.329.119.618.532.328.610.514.80clar.1
viol.3viol.2viol.1hor.3hor.2hor.1clar.3clar.2clar.1
2.2 Instrument Estimation for
Monophony
We made some experiments for the instrument
estimation under the following conditions: The
template of autocorrelation function
of each
)(
kR
q
MUSICAL INSTRUMENT ESTIMATION FOR POLYPHONY USING AUTOCORRELATION FUNCTIONS
145
instrument is made at the point of 20 ms in the
beginning part of a sound, and 100 autocorrelation
functions
are made randomly in the range
from15 ms to 25 ms in the beginning part of the
sound. We made some instrument estimations for
43
and tones. Table 3 shows the estimation
results for
4
C tone. We could obtain the mean
estimation error of 0.8 % for these tones
(
).
)(
kR
p
, CG
5
F
543
,, FCG
3 INSTRUMENT ESTIMATION
FOR POLYPHONY USING
AUTOCORRELATIO
FUNCTIONS
3.1 Separation of Polyphony Using
Comb Filter
The comb filter is written by Eq.(3) and its
block diagram and the frequency characteristic are
shown in Fig.5. We can separate polyphony into each
monophony using the comb filters as shown in Fig.6.
The comb filter
can eliminate one tone
corresponding to the its period
where
one delay
.
)(zH
p
)(
zH
p
spp
fNT /=
/1
1
s
fz =
−
p
N
p
zzH
−
−= 1)( (3)
Because the instrument sound with pitch
is
composed of a fundamental frequency (pitch)
p
f
p
and its harmonic ones
p
. But the
amplitudes of
p
and
q
of each
monophony separated by the comb filters are
changed by the amplitude characteristics of the
comb filters
and , respectively.
f
),3,2( "=nnf
)(' nx )(' nx
)(zH
q
)(zH
p
3.2 Autocorrelation Function of the
Output of a Comb Filter
(a)
(b)
Figure 5: (a) Block diagram of comb filter and (b) its
Frequency characteristic
q
N
q
zzH
−
−= 1)(
p
N
p
zzH
−
−= 1)(
)()()( nxnxnx
qp
+
=
)(' nx
p
)(' nx
q
q
N
q
zzH
−
−= 1)(
p
N
p
zzH
−
−= 1)(
)()()( nxnxnx
qp
+
=
)(' nx
p
)(' nx
q
Figure 6: Separation of polyphony into each monophony
The output of the comb filter is written by )(zH
p
)()()(
pp
Nnxnxny
−
−
=
(4)
The autocorrelation function
of can
be calculated
by using the autocorrelation
functions for the monophony as shown in Eq.(5).
)(kR
po
)(ny
p
By using Eq.(5), we have only the same number of
autocorrelation functions for the templates as the
number of instruments per each tone. We confirmed
that the autocorrelation function of the output of the
comb filter can be calculated by Eq.(5). Figure 7
shows two autocorrelation functions, one of them is
one calculated by using the output of the comb filter
, and the other is calculated by Eq.(5) using
the autocorrelation function
for monophony
)(zH
p
)(kR
1
0
1
0
1
0
1
0
1
0
1
0
1
() () ( )
1
{() ( )}
{( ) ( )}
1
()( )
1
()( )
1
()( )
1
()()
2()( )( ) (5
N
po p p
n
N
p
n
p
N
n
N
pp
n
N
p
n
N
p
n
pp
R k ynynk
N
xn xn N
N
xn k xn k N
xnxn k
N
xn N xn N k
N
xnxn k N
N
xn N xn k
N
Rk RN k RN k
−
=
−
=
−
=
−
=
−
=
−
=
=+
=−−⋅
+− +−
=+
+−−+
−+−
−−+
=−+−−
∑
∑
∑
∑
∑
∑
)
q
when two tones of the polyphony are a clarinet
C
and a horn
E and the comb filter
eliminates the horn E . These
autocorrelation functions are almost same. Figure 8
shows the autocorrelation functions of the output
of the comb filter H for five
instruments in the same condition as Fig.7. Table 4
4
4
)(zH
p
4
)(' nx
p
)(z
+
1−
z
1−
z
1−
z
"
)(nx
p
N
)(ny
p
)(
p
Nnx −
+
++
1−
z
1−
z
1−
z
1−
z
1−
z
1−
z
"
)(nx
p
N
)(ny
p
)(
p
Nnx −
+
p
N
p
zzH
−
−= 1)(
p
f
p
f3
p
f2
p
N
p
zzH
−
−= 1)(
p
f
p
f3
p
f2
shows the values of Eq.(2) when the input sound is
composed of one tone (
) of five instruments and
a horn tone (
), and the tone is eliminated by
4
C
4
E
4
E
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
146

Figure 7: Comparison between autocorrelation function of
output (
) of the comb filter and one
calculated by Eq.5 using autocorrelation function
of
monophony (
:horn, :clarinet)
'
4
C )()(
4
EzH
q
)(kR
4
C
4
E
Figure 8: Autocorrelation functions of output of the comb
filter
for five instruments )()(
4
EzH
q
Table 4 Accumulated differences between the
autocorrelation functions ( )of two
instruments when the input sound is
and the
tone is eliminated by the comb filter
.
)(),( kRkR
qp
44
EC +
4
E
)()(
4
EzH
q
Table 5: Instrument estimation results when the input
sound is composed of one of five instruments (
4
C ) and
horn (
), and the tone is eliminated by the comb
filter
( ).
4
E
4
E
)(zH
q
4
E
monophony
Eq.(5)
comb output
monophony
Eq.(5)
comb output
1000000violin
0100000viola
0010000alt-sax
1500850horn
0000100clarinet
violinviolaalt-saxhornclarinet
1000000violin
0100000viola
0010000alt-sax
1500850horn
0000100clarinet
violinviolaalt-saxhornclarinet
Table 6: Instrument estimation errors.
6.0mean error
4.6
12.7
2.2
4.9
6.0
clarinet
horn
alt-sax
viola
violin
error(%)sound rangeinstrument
6.0mean error
4.6
12.7
2.2
4.9
6.0
clarinet
horn
alt-sax
viola
violin
error(%)sound rangeinstrument
53
BD
−
53
FC
−
53
AD
−
53
BC
−
53
BG
−
0 244872
–1
0
1
clarinet
horn
alt–sax
viola
violin
auto–correlation R(k)
k
the comb filter
(
4
). From these results, we
can realize that each autocorrelation function of the
output of the comb filter for each instrument is
different each other.
)(zH
q
E
3.3 Instrument Estimation for
Polyphony
Using the combination of five instruments, we made
the instrument estimation when two tones are
4
C
and
4
E . Like in the case of monophony, we
made each 100 autocorrelation functions in the
range from 15 ms to 25 ms for two outputs of the
comb filters in Fig.6. Then we
0violin
18.960viola
33.9020.200alt-sax
6.2216.7234.620horn
41.5737.2425.9044.510clarinet
violinviolaalt-saxhornclarinet
C’
4
0violin
18.960viola
33.9020.200alt-sax
6.2216.7234.620horn
41.5737.2425.9044.510clarinet
violinviolaalt-saxhornclarinet
C’
4
calculated Eq.(2) between the autocorrelation
function of the output of the comb filter and the
templates calculated by Eq.(5) for five instruments.
Table 5 shows one example of the instrument
estimation results under the same condition as Table
4. Table 6 shows the each instrument estimation
error for two tones that are made by all the
combinations of five instruments. We could obtain
the mean estimation error of 6% for five
instruments.
MUSICAL INSTRUMENT ESTIMATION FOR POLYPHONY USING AUTOCORRELATION FUNCTIONS
147

4 CONCLUSIONS
We proposed a new musical instrument estimation
of polyphony using autocorrelation functions.
Polyphony can be separated into each monophony
using the comb filters. Using the autocorrelation
functions of the outputs of the comb filters, we can
estimate the instrument by comparing with the
autocorrelation functions of the templates that can be
calculated from the autocorrelation functions of
monophony. We could obtain the mean estimation
error of 6% for five instruments.
As a future work, we’d like to reduce the number
of templates considering the analogous
autocorrelation functions of neighbour tones.
REFERENCES
M.Abe and S.Ando, “Application of loudness/
pitch/timbre decomposition operators to auditory scene
analysis,” Proc. of ICASP.pp.2646-2649, 1996.
G.J.Brown and M.Cooke, “Perceptual grouping of musical
sounds: a computational model,” Journal of New
Music Research, vol.23, no.2 pp.107-132, 1994.
P.Jincahita, “Polyphonic instrument identification suing
independent subspace analysis,” IEEE Int. Conf. on
Multimedia and Xpo (ICME), vol.2, pp.1211-1214,
2004
A.G.Krishna, and T.V.Sreenivas, “Music instrument
recognition: From isolated notes to solo phrases,” Proc.
Of ICASSP, pp.IV265-268, 2004
J.Lee and J.Chun, “Musical instrument recognition using
hidden morkov model,” Conference record of the
Asilomar Conference on Signals, Systems and
Computers, vol.1, pp.196-199, 2002
E.Pollastri, ”A pitch tracking system dedicated to process
singing voice for musical retrieval,” Proc. of IEEE Int.
Conf. on Multimedia and Xpo (ICME) , 2002.
C.Roads, ”Research in music and artificial intelligence,”
ACM computing Survey, vol.17, no.2, pp.163-190,
1985.
C.Roads, ”The Computer Music Tutorial,” MIT Press,
1996.
A.Sterian and G.H.Wakefield, ”Music transcription
systems: from sound to symbol,” Proc. of AAAI-2000
workshop on artificial intelligence and music, July
2000.
Y.Tadokoro and T.Miwa, ”Musical pitch and instrument
estimation of polyphony using comb filters for
transcription,” 4
th
World Multiconference on Circuits,
Systems, Communications and Computers
(CSCC2000), Advance in Physics, Electronics and
Signal Processing Applications, pp.315-319, 2000.
Y.Tadokoro and M.Yamaguchi, “Pitch detection of duet
song using double comb filters,” Proc. of ECCTD’01,
I, pp.57-60, 2001.
Y.Tadokoro, W.Matsumoto and M.Yamaguchi, “Pitch
detection of musical sounds using adaptive comb filters
controlled by time delay,” ICME2002, P03, 2002.
Y.Tadokoro, T.Morita and M.Yamaguchi, “Pitch detection
of musical sounds noticing minimum output of parallel
connected comb filters, “ IEEE TENCON2003, tencon-
072, 2003.
Y.Tadokoro, K.Tanishita and M.Yamaguchi, ”Musical
instrument estimation using linear prediction method,”
Proceedings of the 11
th
International Workshop on
Systems, Signals and Image Processing(IWSSIP’04),
pp.2077-210, September 13-15, 2004.
T.Zhang, ”Instrument classification in polyphonic music
based on timbre analysis,” Proc. of SPIE, vol.4519,
pp.136-147, 2001
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
148
