ROBUST CONTROL OF INDUCTION MOTOR USING FAST

OUTPUT SAMPLING TECHNIQUE

Alemayehu G/E Abera, B. Bandyopadhyay, S. Janardhanan

Systems and Control Engineering

IIT Bombay, Mumbai, INDIA

Vivek Agrawal

Dept. of Electrical Engineering

IIT Bombay, Mumbai, INDIA

Keywords:

Induction motor , fast output sampling, integral action, robust control.

Abstract:

In this paper a design method based on robust fast output sampling technique is presented for the speed control

of induction motor. The nonlinear model of induction motor model is linearized around various operating

points to obtain the linear models. The input of the induction motor is the stator voltages and only the speed is

considered as the output of the systems. A single controller is designed for these linear models. The nonlinear

model of the induction motor is simulated with the proposed controller at these operating points. This method

does not require the state of the system for feedback and is easily implementable.

1 INTRODUCTION

The induction motor is being used in many industrial

applications due to its reliability, ruggedness, and low

cost. Its mechanical reliability is due to the fact that

there is no mechanical commutation(i.e. there are no

brushes nor commutator to wear out as in a DC mo-

tor). Further more it can also be used in volatile envi-

ronments since no sparks are produced as is the case

with the commutator of a DC motor. For these and

other reasons induction motor is widely used in many

electric drive applications. However, the induction

motor presents a challenging control problem. This

is due to the fact that this dynamical system is nonlin-

ear, two of the state variables (rotor ﬂuxes/currents)

are not usually measurable, and due to heating the

rotor resistance varies considerably with a signiﬁ-

cant impact on the system dynamics. High perfor-

mance drives for various applications using induc-

tion motors with vector control have become the pre-

ferred form of motive power in a number of applica-

tions. Vector control transforms the induction motor

into a system that has the characteristics of a sepa-

rately excited DC motor. Success of vector control

techniques depend on the knowledge of instantaneous

magnitude and position of rotating magnetic ﬁeld (or

ﬂux) in the machine. Direct measurement of mag-

netic ﬁeld using search coils, hall effect sensors re-

quire implantation of sensors in the air gap of the ma-

chine and hence result in increased complexity. More-

over, they are prone to errors caused by factors like

temperature variation and noise (Janson and Lorenz,

1992),(Verghese and Sanders).

In order to circumvent direct measurement of the

magnetic ﬂux, a number of ﬂux estimation methods

have been proposed in the last few years (Janson and

Lorenz, 1992),(Sangwongwanich et al.,). All these

methods utilize terminal measurements of voltage and

current along with (or without) rotor speed to arrive

at an accurate estimate of the magnitude and posi-

tion of the ﬂux in the machine. These methods have

been broadly classiﬁed as open loop observers and

closed loop observers to have superior performance

characteristics with respect to robustness and accu-

racy(Janson and Lorenz, 1992). Almost all of the lit-

erature uses more than one of the system states for the

design of the controller.

In this paper a design of robust fast output sampling

controller for induction motor control by measuring

only the speed is proposed. This is done by sampling

the speed signal at a faster rate than the input signal. It

will be shown that using this technique a robous con-

trrol for the multimodel representation of nonlinear

model of the induction motor can be obtained. The

outline of the paper is as follows. Section 2 presents

dynamic model of an induction motor. Section 3 deals

with a brief introduction of fast output sampling con-

trol technique where as the controller design is pre-

sented in Section 4. Section 5 presents simulation re-

sults and discussions followed by the concluding re-

marks.

G/E Abera A., Bandyopadhyay B., Janardhanan S. and Agrawal V. (2005).

ROBUST CONTROL OF INDUCTION MOTOR USING FAST OUTPUT SAMPLING TECHNIQUE.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 25-30

DOI: 10.5220/0001175600250030

 SciTePress

2 DYNAMIC MODEL OF AN

INDUCTION MOTOR

Under the commonly used assumptions, the behavior

of the three phase, four pole, induction motor in the

orthogonal ﬁeld reference frame can be described by

a set of non-linear equations as given below (Kraus,

et al, 2002) ,(Mohan, 2000), (Mohan, 2001)

= σR

+ ω

q s

+ βL

q s

(1)

+βR

+ βL

q r

+ σV

q s

= −ω

− βL

− σR

q s

−σL

+ βR

q r

+ σV

q s

= βR

− γL

q s

− γR

+ω

q r

− σL

q r

− βV

q r

= βL

+ βR

q s

− ω

+σL

− γR

q r

− βV

q s

− T

)

q s

− i

q r

) .

where i

, i

q s

are stator currents, i

, i

q r

are rotor cur-

rents, V

, V qs are stator voltages, ω

is rotor angle

velocity, ω

is synchronous speed, T

, T

are electro-

magnetic and load torques, J

is inertia of the rotor,

p is number of poles, α, β, σ and γ are all positive

constants deﬁned as:

α = L

− L

β = L

/α,

σ = L

/α,

γ = L

/α

where L

and L

are stator and rotor inductances, R

and R

are stator and rotor resistances and L

is the

mutual inductance. The output is the rotor speed.

3 ON FAST OUTPUT SAMPLING

FEEDBACK

3.1 Review on Fast Output

Sampling Feedback

The problem of simultaneous stabilization has re-

ceived considerable attention in the literature. Given

a family of plants in state space representation

(Φ

, Γ

) , i = 1, · · · , M, ﬁnd a linear state feed-

back gain F such that (Φ

+ Γ

F ) is stable for i =

1, · · · , M , or determine that no such F exists. But

the method is of use only in the case where whole

state information is available.

One way of approaching this problem with incom-

plete state information is to use observer based control

laws, i.e. dynamic compensators. The problem here

is that the state feedback and state estimation cannot

be separated in face of the uncertainty represented by

a family of systems. Assuming that a simultaneously

stabilizing F has been found, it is possible to search

for a simultaneously stabilizing full order observer

gain, but this search is dependent on the F previously

obtained. If no stabilizing observer for this state feed-

back exists, nothing can be said because there may ex-

ist stabilizing observers for different feedback gains.

With the Fast output sampling approach proposed

by (Werner and Furuta, 1995) it is generically possi-

ble to simultaneously realize a given state feedback

gain for a family of linear, observable models. For

fast output sampling gain L realize the effect of state

feedback gain F , ﬁnd the L such that (Φ

+ Γ

LC)

is stable for i = 1, · · · , M, If there exist a set of

F ’s, there should exist a common L for given fam-

ily of plants. One of the problems with this approach

is that large feedback gains tend to render the system

very noise -sensitive. To overcome this problem the

design problem can be posed as a multi-objective op-

timization problem in an LMI formulation proposed

by (Werner, 1998).

Consider a plant described by a linear model

= Ax + Bu, (2)

y = Cx, (3)

with (A, B) controllable and (C, A) observable.

Assume the plant is to be controlled by a digital con-

troller, with sampling time τ and zero order hold, and

that a sampled data state feedback design has been

carried out to ﬁnd a state feedback gain F such that

the closed loop system

x (kτ + τ ) = (Φ

+ Γ

F )x (kτ ) , (4)

has desired properties. Hence Φ

= e

Aτ

and

dsB. Instead of using a state observer,

the following sampled data control can be used to re-

alize the effect of the state feedback gain F by output

feedback. Let ∆ = τ /N, and consider

u(t) = [L

· · · , L

N−1

]







y (kτ − τ )

y (kτ − ∆)







= Ly

, (5)

for kτ ≤ t < (k + 1)τ , where the matrix blocks

represent output feedback gains, and the notation

ICINCO 2005 - ROBOTICS AND AUTOMATION

L, y

has been introduced for convenience. Note that

1/τ is the rate at which the loop is closed, whereas

output samples are taken at the N -times faster rate

1/∆.

To show how a fast output sampling controller (5

) can be designed to realize the given sampled-data

state feedback gain, we construct a ﬁctitious, lifted

system for which (5 ) can be interpreted as static out-

put feedback. Let ( Φ, Γ, C ) denote the system (2) at

the rate 1/∆. Consider the discrete-time system hav-

ing at time t = kτ the input u

= u(kτ), state x

x(kτ) and output y

k+1

= Φ

+ Γ

, (6)

k+1

= C

+ D

, (7)

where







CΦ

N−1







, D







CΓ

N−2

j=0







Assume that the state feedback gain F has been de-

signed that (Φ

+ Γ

F ) has no eigenvalues at the ori-

gin. Then, assuming that in intervals kτ ≤ t < kτ +τ

u(t) = F x(kτ), (8)

one can deﬁne the ﬁctitious measurement matrix

C(F, N) = (C

+ D

F )(Φ

+ Γ

F )

−1

, (9)

which satisﬁes the ﬁctitious measurement equation

= Cx

. For L to realize the effect of F , it must

satisfy

LC = F. (10)

Let ν denote the observability index of (Φ, Γ). It

can be shown that for N ≥ ν, generically C has full

column rank, so that any state feedback gain can be

realized by a fast output sampling gain L.

If the initial state is unknown, there will be an error

∆u

= u

- F x

in constructing the control signal

under state feedback. One can verify that the closed

loop dynamics are governed by



k+1

∆u

k+1





+ Γ

F Γ

0 Ψ(L)



∆u



(11)

where Ψ(L) = LD

− F Γ

Thus, one can say that the eigenvalues of the closed

loop system under a fast output sampling control law

(5) are those of Φ

+ Γ

F together with those of

− F Γ

One feature of fast output sampling control that

makes it attractive for robust controller design, is the

fact that a result similar to the above can be shown to

hold when the same state feedback is applied simul-

taneously to a family of models representing different

operating conditions of the plant.

3.2 Integral Action

The fast output controller (5), can be used to realize

the effect of state feedback. If step disturbances are

to be rejected with zero steady state error, then the

controller must integrate the tracking error. A pure

state feedback control law does not include integral

action, but can be made to do so by introducing a

new state ζ that integrates the error (Werner, 1996).

This can be realize in discrete time using:

k+1

= ζ

+ r

− y

where r

stands for the sampled reference input. A

discrete time state space representation for the aug-

mented system is

¯x(k + 1) =

Φ¯x(k) +

Γu(k) +

r(k), (12)

where ¯x(k) = [x(k)

]

and

Φ =



−C I



Γ =









State feedback gain F and the integrator gain F

can

be collected from a new state feedback gain

F = [F

] to yield the control law

u(k) =

F x(k) = F x(k) + F

= Ly

+ F

(13)

with a resulting closed loop matrix:

F =



+ Γ

F Γ

−C I



3.3 Multimodel Synthesis

For multimodel representation of a plant, it is nec-

essary to design controller which will robustly stabi-

lize the multimodel system. Multimodel representa-

tion of plants can arise in several ways. When a non-

linear system has to be stabilized at different operat-

ing points, linear models are sought to be obtained

at those operating points. Even for parametric un-

certain linear systems, different linear models can be

obtained for extreme points of the parameters or for

ROBUST CONTROL OF INDUCTION MOTOR USING FAST OUTPUT SAMPLING TECHNIQUE

family of different models. The models are used for

stabilization of different machine models

Now consider a family of plant S = {A

deﬁned by

˙x = A

x + B

u, (14)

y = C

x, i = 1, · · · , M. (15)

By sampling at the rate of 1/△, we get a family of

discrete-time systems {Φ

, Γ

, C

Consider the family of discrete-time systems given

by Eqns.(14) and (15) having at time t= kτ the input

= u(kτ), state x

= x(kτ) and output y

k+1

= Φ

τ i

+ Γ

τ i

, (16)

k+1

= C

+ D

, (17)

Assume that (Φ

τ i

, Γ

) are controllable. Then we

can ﬁnd a robust state feedback gains F such that

(Φ

τ i

+ Γ

F ) has no eigenvalues at the origin.

Then, assuming that in intervals kτ ≤ t < kτ + τ

u(t) = F x(kτ), (18)

one can deﬁne the ﬁctitious measurement matrix

(F, N) = (C

+ D

F )(Φ

τ i

+ Γ

τ i

F )

−1

, (19)

which satisﬁes the ﬁctitious measurement equation

= C

. For robust fast output sampling gain L to

realize the effect of F , it may satisfy

= F, i = 1, · · · , M. (20)

The Eqn.(20) can be written as

∽

, (21)

where

∽

= [

· · · C

] ,

∽

= [

F F · · · F

] .

The robust state feedback gain F can be obtained

from the augmented matrix (12) by considering a fam-

ily of plants

S =





, deﬁned by.

¯x(k + 1) =

¯x(k) +

u(k) +

r(k), (22)

3.4 An LMI Formulation of the

Design Problem

When this idea is realized in practice i.e. fast out-

put sampling gain L have been obtained by realizing

the state feedback gain F , two problems are required

to be addressed. The ﬁrst one is apparent from(11).

With this type of controller, the unknown states are

estimated implicitly, using the measured output sam-

ples and assuming that initial control is generated by

state feedback. If initial state causes an estimation

error, then decay of this error will be determined by

the eigenvalues of the matrix (LD

− F Γ

τ i

) which

depends on L and whose dimension equals the num-

ber of control input. For stability these eigenvalues

have to be inside the unit disc, and for fast decay they

should be as close to the origin as possible. This prob-

lem must be taken into account while designing L.

The second problem is that the gain matrix L may

have elements with large magnitude. Because these

values are only weights in linear combination of out-

put samples, large magnitudes do not necessarily im-

ply large control signal, and in theory and noise free

simulation they pose no problem. But in practice they

amplify measurement noise, and it is desirable to keep

these values low. This objective can be expressed by

an upper bound ρ on the norm of the gain matrix L.

When trying to deal with these problem, it is bet-

ter not to insist on an exact solution to the design(20):

one can allow a small deviation and use an approx-

imation LC

≈F, which hardly affects the desired

closed-loop dynamics, but may have considerable ef-

fect on the two problems described above. Instead of

looking for an exact solution to the equalities, the fol-

lowing inequalities are solved

kLk < ρ

kLD

− F Γ

τ i

k < ρ

, i = 1, · · · , M,

kLC

−F k < ρ

3i.

(23)

Here three objectives have been expressed by upper

bounds on matrix norms, and each should be as small

as possible. The ρ

small means low noise sensitivity,

small means fast decay of estimation error, most

important - ρ

-small means that fast output sampling

controller with gain L is a good approximation of the

originally designed state feedback controller. If ρ

0 then L is exact solution.

Using the Schur complement, it is straight forward

to bring these conditions in the form of LMI (Linear

Matrix Inequalities) proposed by (Werner, 1996)



−ρ

I L

−I



< 0,



−ρ

I (LD

− F Γ

τ i

)

(LD

− F Γ

τ i

)

−I



< 0,



−ρ

I (LC

−F)

(LC

−F)

−I



< 0. (24)

In this form, the function mincx() of the LMI con-

trol toolbox for MATLAB can be used immediately

ICINCO 2005 - ROBOTICS AND AUTOMATION

to minimize a linear combination of ρ

, ρ

. The

following approach turned out to be useful. If the

actual measurement noise is known, the magnitude

of L is ﬁxed accordingly. Likewise eigenvalues of

(LD

− F Γ

τ i

) less than 0.05 cause no problem. So

we can ﬁx ρ

, ρ

and only ρ

is minimized subject to

these constraints.

In this form the LMI Tool Box of MATLAB can

be used for synthesis as suggested by (Gehenet, et al.,

1995).

The fast output sampling feedback controller ob-

tained by the above method requires only constant

gains and hence is easier to implement. The example

of multi machine system dynamics is used to demon-

strate the method.

4 CONTROLLER DESIGN

The design procedure assumes a linear model. The

linearization was carried out about an operating point

of the non-linear induction motor model (1), with the

data provided in the appendix for three induction ma-

chine models.

Since the nonlinear system is to track a constant

reference speed, the linear system composed of the

error states, obtained at this nominal speed would be

equivalently required to track a reference of zero. The

continuous linear models are discretized and the dis-

crete models are represented by the following equa-

tion

∆x(k + 1) = Φ

τ i

∆x(k) + Γ

τ i

∆u(k), (25)

∆y(k) = C

∆x(k), i = 1, 2, 3 (26)

where

∆x(k) = [

∆i

q s

∆ω

∆i

q s

]

∆u(k) = [

∆V

q s

]

with the speed of the induction machines being the

output. The appropriate control action can now be

computed using Eqn. (13).

However, for tracking of a reference speed, the in-

tegral action F

would require the error in the speed

of the system. This is realized by comparing the ac-

tual speed with the reference speed.

and

∆u(k) = F

ζ (k) + L∆y

(27)

From the incremental control ∆u(k), actual control

u(k) is obtained.

u(k) = u

+ ∆u

5 SIMULATION RESULTS AND

DISCUSSIONS

The system (1) is linearized about three operating

points using MATLABr to get a linear system of

form (14), Discretization of (A

, B

, C

) at an inter-

val of τ = 0.04 sec . and adding an integrator leads

to the augmented system (22) for which a common

state feedback gain must be found. This problem

can be solved by convex programming methods,for

which software tools are available in the LMI toolbox

for Matlab(Gehenet, et al., 1995). This yields a state

feedback gain:

F = [F F

] =



−0.1227 25.8298 37.6501 · · ·

−2.9221 72.7314 42.1827 · · ·

· · · 27.5299 38.8149 7.4603

· · · 74.0091 42.0990 1.2915



Using (21), the fast output sampling gain is calcu-

lated as

L =



−6.128 22.643 −29.69 5.858

−2.075 10.899 −23.982 12.78

22.365 −9.549 −21.152 6.531

19.153 −15.18 −19.264 13.476

18.73 −6.51 −18.668 11.02

21.415 −10.677 −23.443 10.585

21.403 −31.972 12.87

22.504 −33.03 15.132



Now, using Eqn. (27), ∆u(k) is obtained and u(k) for

the nonlinear model which is u

+ ∆u(k) is also ob-

tained. This is used in the simulation of the nonlinear

model with 10% change in load.

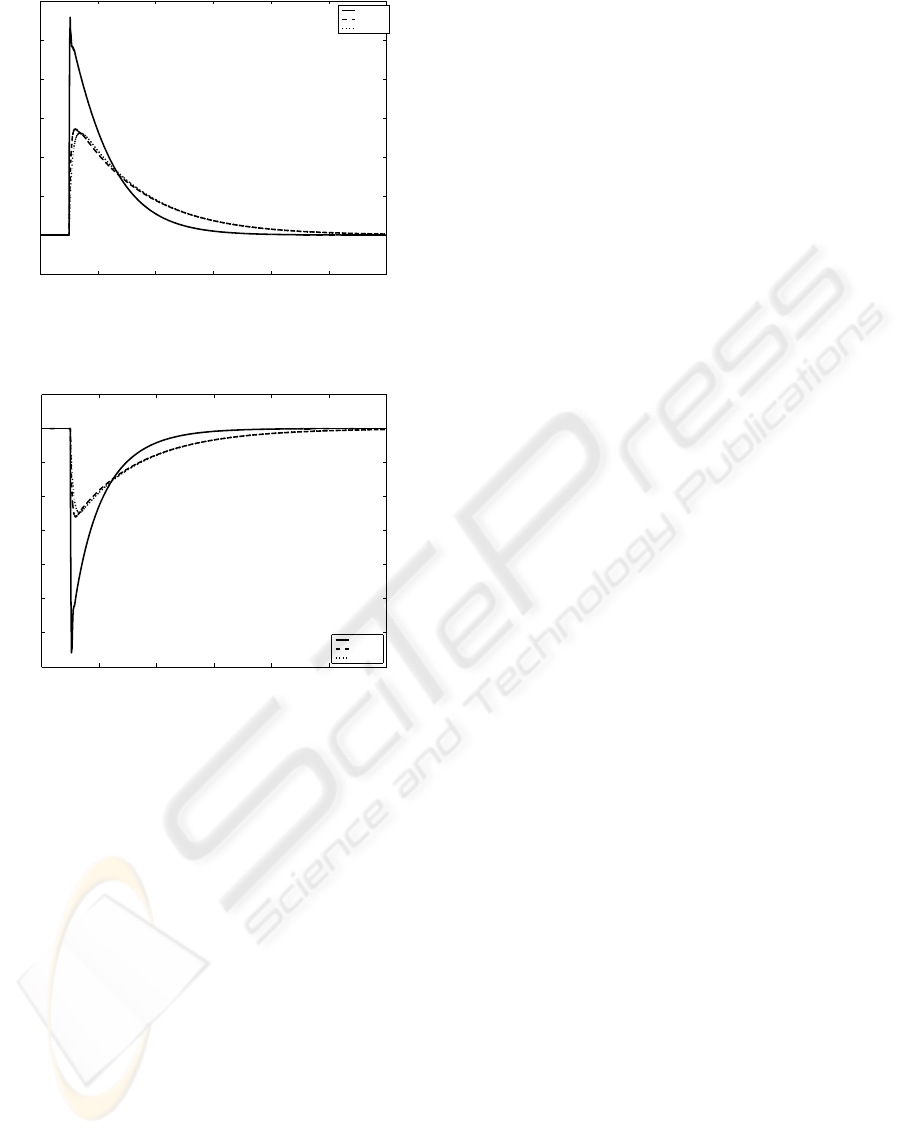
Fig. (1) shows the speed proﬁle of the closed loop

systems of all three models for the load disturbance of

-10%. Fig. (2) shows the speed proﬁle of the closed

loop systems of all models for the load disturbance of

+10%. It can be seen that in all cases the designed

robust controller is able to bring back the rotor speed

to the rated value.

6 CONCLUSION

In this paper, a design scheme of the control of in-

duction motor using fast output sampling control is

developed. The rotor speed is taken as output. The

output feedback control is applied at an appropriate

sampling rate to the nonlinear model of the plant.

As shown in plots, the proposed controller is able

to stabilize the speed around the operating points for

the change in load torque (T

) in spite of change in

plant model.

ROBUST CONTROL OF INDUCTION MOTOR USING FAST OUTPUT SAMPLING TECHNIQUE

0 5 10 15 20 25 30

1615

1620

1625

1630

1635

1640

1645

1650

time in sec.

speed in rpm

plant−1

plant−2

plant−3

Figure 1: Response of various models to -10% load dis-

tubance

0 5 10 15 20 25 30

1585

1590

1595

1600

1605

1610

1615

1620

1625

time in sec.

speed in rpm

plant−1

plant−2

plant−3

Figure 2: Response of various models to +10% load dis-

tubance

REFERENCES

Gahenet, P., Nemirovski, A., Laub, A. J. and Chilali, M.,

(1995), LMI Tool Box with for Matlab The Math

works Inc.: Natick MA.

Janson, P. L. and Lorenz, R. D., (1992), A physically in-

sightful approach to the design and accuracy assess-

ment of ﬂux observers for ﬁeld oriented induction ma-

chine drives EEE-IAS annual meeting record. ,570–

577.

Krause, P. C., Wasynczuk, O. and Sudhoff, S. D., (2002),

Analysis of Electric Machinery and Drive Systems

IEEE Press

Mohan N., (2000), Electric Drives : An Integrative Ap-

proach MNPERE Minneapolis.

Mohan N., (2001), Advanced Electric Drives : Analysis,

Control and modeling using Simulink MNPERE Min-

neapolis.

Sangwongwanich, S., Yonemoto, T., Furuhashi, T. and

Okuma, S., Design of sliding observer for robust es-

timation of rotor ﬂux of induction motors Proceeding

of IPEC,Tokyo, 1235–1242..

Verghese, G. C. and Sanders, S. R., Observers for ﬂux es-

timation in induction machine IEEE Trans. on Indus-

trial Electronics , 35(1):85–94.

Werner, H., (1996), Robust Control of a Laboratory Flight

Simulator by Non-dynamic Multi-rate Output Feed-

back, Proceeding of CDC , Kobe, Japan, 1575–1580.

Werner, H.,(1998), Multimodel robust control by fast output

sampling - LMI approach. Automatica, 34(2), 1625–

1630.

Werner, H., and Furuta, K., (1995), Simultaneous Stabi-

lization based on output measurement Kybernetika,

31, 395–411.

APPENDIX

A INDUCTION MOTOR

PARAMETERS

The following parameters are used for simulation of

the induction motor.

Power : 3 HP/2.4 KW

Voltage: 460 Volts (L-L, RMS)

Frequency: 60 Hz

Phases: 3

Full- Load Current: 4 A

Full- Load Speed: 1710 rpm

Full- Load Efﬁciency: 88.5%

Power Factor: 80.0%

No. of Poles: 4

slip=1.72%

Model Parameters Model-1 Mode-2 Mode-2

Rr 1.4Ω 46.2Ω 74Ω

Rs 1.2Ω 1.43Ω 1.77Ω

Xls 4.5Ω 6.72Ω 5.25Ω

Xlr 4.5Ω 6.72Ω 4.57Ω

Xm 142Ω 158Ω 139Ω

ICINCO 2005 - ROBOTICS AND AUTOMATION