IDENTIFICATION OF STRUCTURE IN NONDETERMINISTIC

CYCLIC SOCIAL CONVENTIONS

Hürevren Kılıç

Department of Computer Engineering, Atılım University,Kızılcaşar Köyü Incek, Gölbaşı, Ankara, Turkey

Keywords: Social conventions, S

ystem modeling and identification, Time series.

Abstract: A polynomial-time algorithm for the identification of interaction and memory structures in discrete valued,

nondeterministic, cyclic social behavior data is developed. The output of the probabilistic search algorithm

is the strategy update function for each individual automaton agent in given population. For our modeling

purpose, we used automata networks model and added “block-extended memory” property to its original

definition. The approach can also be considered as a limit cycle construction technique for discrete

dynamical systems.

1 INTRODUCTION

Understanding the nature of social conventions in

human (or agent) societies may contribute to

obtaining more natural and better design forms in

synthetic (or in virtual) environments. The study on

social conventions is not new (Ullman-Margalit,

1977), but it is relatively new in the context of

artificial intelligence and multiagent systems

(Walker and Wooldridge, 1995); (Shoham and

Tennenholtz 1997); (Coen, 2000); (Delgado, 2002).

“A social law is a restriction on the set of actions

available to agents. If it restricts the agents’ behavior

to a particular action (or strategy) it is called social

convention” (Shoham and Tennenholtz, 1997). From

this definition, one may conclude that the existence

of a social convention generated by an agent

population requires all agents to reach (or converge)

to the same state at time t. On the other hand, some

social interaction forms may contain repetitive

patterns of individual and/or collective action

(strategy) choices while they may never evolve into

a mature social convention form at all. Such time-

distributed, nondeterministic, cyclic regular behavior

converging to a limit cycle of some length k >1 can

still be a solution to recurrent coordination

problems. From the game-theoretic perspective, they

are the collection of interacting meta-strategies

enabling some intended flexible strategy changes.

The identification of interaction topology (or

neighborhood structure) among such agents

producing what we call, cyclic social convention (or

timed social equilibrium) behavior may provide

useful information feedback for possible online

emergent design solutions. And, the mechanisms

producing them are worth to be investigated.

Automata Network (AN) is a useful

athematical model for analyzing such global

dynamics emerging from collective behavior of local

components (Aspray and Burks, 1987).

Identification of an AN that can generate given

arbitrary collective behavior sequence problem is a

typical inverse problem (Wolfram, 1984). In this

paper, we used a modified AN model in which the

automata components (i.e. agents) are not

memoryless. By this way, the model fits better into

our cyclic social convention definition. The inverse

problem has been worked on different research

domains by using different subclasses of the

Automata Networks model like cellular automata,

non-uniform cellular automata and Boolean

networks (Langton, 1986); (Adamatzky, 1994);

(Akutsu et.al., 2000); (Ideker et.al., 2000). In

(Ideker et.al., 2000), it was pointed out that the

inverse problem of finding minimum neighborhood

automata network that can generate given

deterministic sequence can be considered as the NP-

Complete problem of set-covering (but without

giving a formal proof). In (Fitoussi and Tennenholtz,

2000), it has been proven that the “automatic

synthesis of social laws” problem is NP-Hard. In this

paper, our aim is not to find an agent interaction

topology with minimum interaction neighborhoods

but to identify a topology by using apriori

knowledge about the relation between the

neighborhood and memory parameters of the

355

Kılıç H. (2005).

IDENTIFICATION OF STRUCTURE IN NONDETERMINISTIC CYCLIC SOCIAL CONVENTIONS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 355-359

DOI: 10.5220/0001175903550359

 SciTePress

system. Simply, the neighborhood/memory relation

is represented in the form of a binomial distribution

function. For our AN identification purpose, we

proposed a probabilistic search algorithm called

Nearest Neighbors Recent Values (NNRV) that

enables the generation of arbitrarily given discrete-

valued, nondeterministic, cyclic behavior sequence.

Note that the approach does not consider any

optimization criterion and for the same sequence

data one may obtain different topologies. However,

the obtained topologies show the general

characteristics defined by given binomial

distribution function.

Section 2 includes formal definition of our

modified AN model. Section 3 describes the NNRV

identification algorithm. Section 4 is the conclusion.

2 THE MODEL

Let I be a finite set of vertices. An automata network

can be defined on I as a triplet A = (G, Q, (f

: i

∈

I ))

where

• G = (I, V) is a graph showing the interaction

topology between vertices where

×⊂

. A finite neighborhood is

defined as V

= {j

∈

I : (j, i)∈V} for any

∈I. The neighborhood system is defined by

V = {(j, i) : j

∈V

, i

∈

I}.

•

is the finite set of states.

• f

: is the state transition function

for vertex i. Here, the f

→

function determines

the next state of i from the current states of

the neighbors of i. The global transition

function F :

is defined on the set

of configurations Q

QQ →

with synchronous

updates (Goles and Martinez, 1990).

Synchronous update requires all vertex values to

be updated simultaneously. The dynamics of

synchronous update can be given by x(t+1) =

(x(t)) whose component is x

(t+1) = f

(t) :

j∈V

The above definition can be extended to an

automata network with block extended memory. For

this purpose, we need to redefine the strategy update

function f

. For a given j∈V

, let P

= q

…q

be a finite sequence of state values of length l

where l ∈N

and q

∈Q for all 1 ≤ s ≤ l. Then, the

size of the memory pattern for vertex i is

= ∑P

where j takes values from 1 to |V

The state transition function for vertex i using

“block extended memory” is f

: . As a

consequence, the dynamics of the

component in

synchronous update mode becomes:

→

(t+1)=f

(t), x

(t-1), x

(t-2)……x

(t-|P

|+1):j

∈

)

In the context of interacting social agents, the set

Q defines agent strategies; V

is the set of agents in

agent’s interaction neighborhood; and f

is the

deterministic strategy update function for the i

agent which may not necessarily be the same for all

agents. One can recognize the existing redundancy

in the accounting of the memory usage. Each

neighbor of say automaton j has the history j

accounted in its memory usage. It is necessary due

to the private nature of observations made by

independent autonomous automaton agents.

However, it should be clear that the agents are

assumed to cooperate (but not compete) in sharing

their private history information.

Definition 1. A cyclic sequence S with period T

is an ordered list of global configurations, S = x(0),

x(1), …, x(s), … where s

∈

N, x(s)∈Q

and x(s) =

x(s mod T).

Definition 2. A cyclic sequence S with period T

is nondeterministic iff there exists s, t

∈N and 0 ≤

s < t < T such that (x(s) = x(t))

(x(s+1) ≠

x(t+1)) holds, otherwise it is deterministic.

⇒

Lemma 1. There exists a nondeterministic cyclic

sequence S with period T such that one cannot find

any automata network A working in synchronous

update mode and without using block extended

memory (i.e. |P

| = 1 for all j ∈ V

and i∈I ) that

can generate S.

Proof. Let x(s), x(t), x(s-1) and x(t-1) be

configurations in sequence S where s≠ t, x(s)≠x(t)

and x(s-1)=x(t-1). Then, there exist at least one

vertex i of A such that x

(s)≠x

(t) and x

(s-1)=x

(t-1).

However, x

(s)≠x

(t) implies f

(s-1): j∈V

) ≠

(t-1): j

∈

) which contradicts with the existence

of x

(s-1)=x

(t-1) for all i

∈

An implication of Lemma 1 is the existence

cyclic social convention forms that cannot be

generated by reflexive, memoryless society of agents

that are updating their strategies synchronously. A

simple example binary-valued, nondeterministic

cyclic sequence showing this fact is: 00Æ00Æ10

where T=3. If there is no such memory usage

restriction on agents, any such arbitrarily given

cyclic sequence can be generated.

Lemma 2. Given a nondeterministic cyclic

sequence S with period T, one can always find an

automata network A working in synchronous update

mode and with block extended memory size of at

most O(T

|I|

) that can generate S.

Proof. Simply, the cyclicity of the sequence

provides a memory of size T for each individual

automaton agent and this makes the generation of

the given nondeterministic sequence trivial. The

upper bound for memory usage can be reached if the

network A is fully connected. In this case, each state

transition rule of the strategy update function

the i

agent uses the whole pattern information,

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

356

T*|I|, of the sequence S. This implies O(T

*|I|)

amount of memory per agent and O(T

*|I|

) in total.

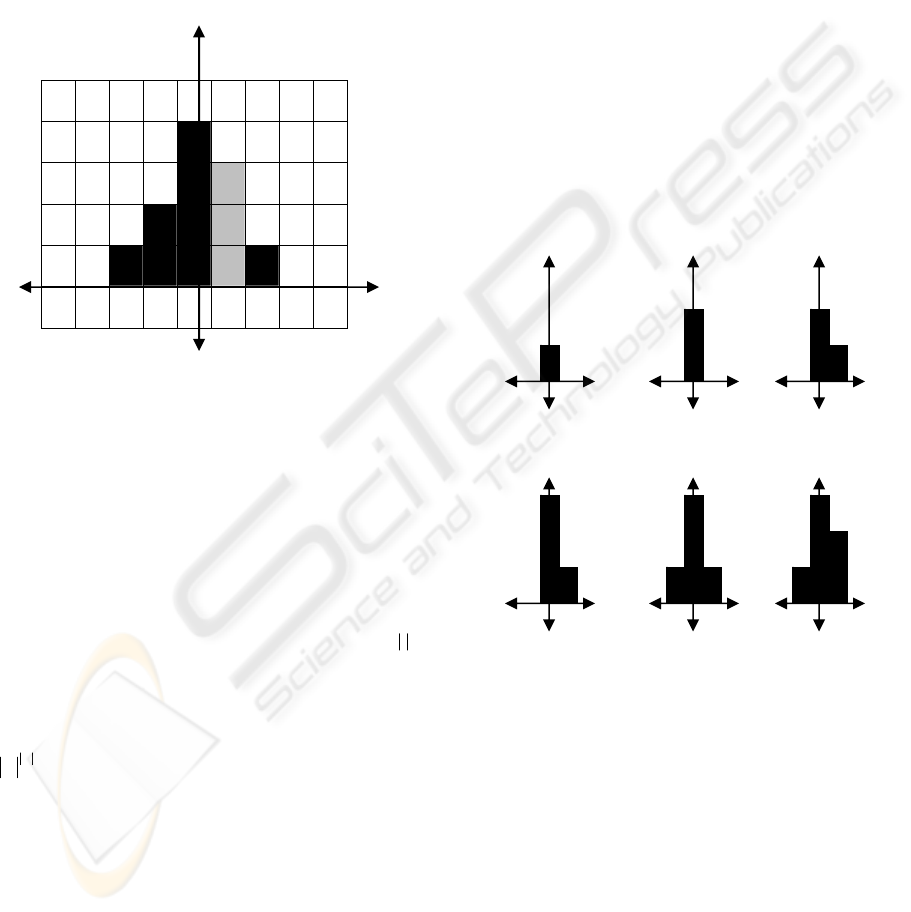
In Figure 1, one can see an example

neighborhood/memory pattern for an individual

automaton i. The horizontal axis defines neighbor

vertices of vertex i (including itself). The vertical

axis, on the other hand, defines the memory patterns

used by vertex i. The gray-colored column P

(i),(i+1)

the memory pattern generated by vertex (i+1) and

used by vertex i. From Figure 1, P

(i),(i+1)

= 3, |V

| = 5

and the total size of memory patterns for i: Z

= 11.

Figure 1: A neighborhood/memory pattern for an

automaton i

3 THE ALGORITHM

Before describing the algorithm, we may need to

figure out the number of possible automata network

neighborhood topologies and potential individual

automata definitions to be searched. Since the

system has |I| number of automata, the number of

possible network neighborhood topologies is:

An automaton i with our block extended memory

definition has |Q| states and decides on its next state

by looking at Z

size memory pattern. Then, the

number of possible fully-defined automaton for i is:

. The search space size is huge and one can

find more than one different automata network

definition that can generate the given

nondeterministic cyclic sequence. Different

solutions are characterized by how individual

conflicts (defined below) are handled by the

algorithm. Note that each resolved conflict requires

some extension on memory pattern of the automaton

which implies an evolution of possibly partially-

defined automaton. The evolution occurs only on

G’s connection topology and on the state transition

rule space (i.e. f

). The states (q∈Q) and the number

of automaton (|I|), on the other hand, are fixed.

Definition 3. Let A(t) be a partially-defined

automata network at time t. Then, the next state

value required to be generated by automaton i of A(t)

is x

(t+1). Let P

be a memory pattern value valid at

time t. If there exist a state transition rule P

Æ q

(where q

∈

Q) defined by f

at time t such that

q≠x

(t+1) then we say that reading x

(t+1) causes an

individual conflict for the automaton i at time t.

In our approach, individual automaton conflicts

can be resolved by neighborhood extension and/or

through memorization. Neighborhood extension can

be thought analogous to increase of cooperation

among ordered automaton units. Then, the

cooperation/memorization structure of an automaton

i can be defined by movements in neighborhood

and/or memory directions of a 2-D memory pattern

space. Figure 2 shows an example time evolution for

memory pattern P

of an automaton i.

“Does automaton agent need to the others for

generating its local sequence data?” As can be

drawn from Lemma 2, the answer is: No, because

given sequence S is cyclic. In other words, when V

= {i} for all i

∈

I heand |P

| = T for all j∈V

, t cyclic

sequence S can be generated without any agent

cooperation. Nevertheless, an automaton with

bounded memorization ability may achieve its

sequence generation task through cooperation. But

this time, generation of S cannot be guaranteed.

Remember the amnesia case when |P

|=1 for all

∈

. As a result, if an automaton agent does not

Memory

Interaction

Neighborhood

Automaton agent i

t=2 t=3

t=1

t=4

t=5 t=6

Figure 2: An example memory pattern evolution

IDENTIFICATION OF STRUCTURE IN NONDETERMINISTIC CYCLIC SOCIAL CONVENTIONS

357

prefer cooperation then it should be able to

memorize the old.

What can be a more realistic representation of

automaton neighborhood/memorization structure?

The answer depends on the characteristics of the

generator of sequence S which is wanted to be

identified. In our approach, we considered basic

space (i.e. physical distance) and time (i.e.

recentness) costs. We assumed that automaton tends

to resolve its conflicts by extending its neighborhood

to its nearest neighbors and recent values can be

remembered more easily. We implement this idea by

our Nearest Neighbors Recent Values (NNRV)

algorithm (see Figure 3). It selects the recent

memory value of the next nearest automaton to the

current one as the candidate for resolving the current

automaton’s conflict. Our implementation of NNRV

based on memory patterns showing binomial

distribution characteristics. As a consequence, the

conflict resolver selection process generated

evolving sand pile like memory patterns (see Figure

2).

The magnitude and spread values of sand piles

are upper-bounded by T and |I|, respectively. The

second input of the algorithm (i.e. p) defines the

neighborhood/memory characterization for each

automaton agent. It is the probability of using the

candidate automaton’s recent value for resolving

current automaton’s individual conflict. The

algorithm executes a probabilistic search in the

space until it resolves all conflict cases. p=1 is the

no-cooperation case where the automaton tries to

resolve its conflicts by itself. In other words,

memory pattern is extended only in memory axis

direction of the current automaton. When p is close

to zero, the automaton mostly prefers cooperation to

memorization. In this case, the spread of the

distribution is dominant over its magnitude. In the

algorithm, we assumed that the p value does not

change by time and it is the same for all automaton

units.

ALGORITHM NNRV

Input:Nondeterministic Sequence (S),

Binomial Dist. Prob. (p)

Output: Automata Network (A)

Initialize: For each column of S,

establish one automaton of A with

initially empty state transition rule

set;

For each automaton i of A {

Our approach can also be considered as a general

purpose limit cycle construction technique for

discrete dynamical systems. However, one may need

to find more realistic memory formation models. For

such purpose, he/she may need to consider

domain/problem specific characteristics of the

sequence data.

(0) = x

(0);

For each config x(j) of S where j > 0

For each config x(k) of S from x(0)

to x(j-1)

if ( x

(j)!=x

(k)) then

while (P

(j)==P

(k)) {

Find i’s next Nearest

Neighbor’s most Recent

“not memorized yet” Value

(r) with probability p;

Extend P

using x

(r);

}

if P

is extended then

extract state transition rules

for automaton A

from S using P

}

Figure 3: Pseudo-code for the NNRV algorithm.

Let m=T (cycle period) and n=|I| (# of automata).

Then, the worst-case time complexity of the above

algorithm can be defined as: [O(m

n) for the For

loops]*[O(mn) for checking the equivalence of

patterns P

(j) and P

(k)]*[O(mn) for conflict

resolution by extending pattern P

] = O(m

) which

is polynomial-time.

4 CONCLUSION

A new discrete-valued, nondetermistic and cyclic

social convention definition is introduced. It is

shown that the structure behind such timed social

equilibrium forms can be investigated by the use of

automata networks model. While doing this, we

added block extended memory property to the

original automata networks definition. It is shown

that for any nondeterministic cyclic sequence data,

one can find an automata network definition that can

generate it while working in synchronous update

mode using block extended memory. For our

structure identification purpose, we developed a

polynomial time probabilistic automata network

search algorithm with time complexity, O(m

)

where m is the cycle length and n is the population

size. The algorithm identifies an automata network

whose neighborhood/memory characteristic is

defined by the parameter (p) of binomial distribution

function. Specifically, we may conclude that the

identification can be achieved even without

cooperation between automaton agent units.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

358

REFERENCES

Adamatzky, A., 1994. Identification of Cellular Automata,

Taylor & Francis, United Kingdom.

Akutsu, T., Miyano, S., Kuhara S., 2000. Inferring

qualitative relations in genetic networks and metabolic

pathways, Bioinformatics, Vol 16(8), pp 727-734.

Aspray, W., Burks, A.W. 1987. Papers of John Von

Neumann on Computing and Computer Theory, MIT

Press, Cambridge Mass.

Coen, M.H., 2000. Non-deterministic social laws,

Proceeding of AAAI-00, AAAI Pres, pp 15-21.

Delgado, J. 2002. Emergence of social conventions in

complex networks, Artificial Intelligence, 141, pp 171-

185

Fitoussi, D., Tennenholtz, M., 2000. Choosing social Laws

for multi-agent systems: Minimality and simplicity,

Artificial Intelligence, 119(1), pp 61-101.

Goles, E., Martinez S., 1990. Neural and Automata

Networks: Dynamical Behaviour and Applications,

Kluwer Academic Publishers, The Netherlands.

Ideker, T.E., Thorsson V., Karp, R.M., 2000. Discovery of

Regulatory Interactions through Perturbation:

Inference and Experimental Design, Proc. of Pacific

Symposium on Biocomputing 5, pp 302-313.

Langton, C., 1986. Studying Artificial Life with Cellular

Automata, Physica D, Vol. 22, pp 120-149.

Shoham, Y., Tennenholtz M., 1997. On the emergence of

social conventions: Modeling, analysis and

simulations, Artificial Intelligence, 94, pp 139-166.

Ullman-Margalit, E., 1977. The emergence of norms,

Oxford Univ. Press, Oxford.

Walker, A., Wooldridge, M., 1995. Understanding the

emergence of conventions in multi-agent systems in

V.Lesser (Ed.), Proc. 1

International Conference on

Multi-Agent Systems, AAAI Press, pp 384-389.

Wolfram, S., 1984. Universality and Complexity in

Cellular Automata, Physica D, Vol. 10, pp 1-35.

IDENTIFICATION OF STRUCTURE IN NONDETERMINISTIC CYCLIC SOCIAL CONVENTIONS

359