WALSH TRANSFORM AS METHOD OF MIMO SYSTEMS
IDENTIFICATION
Andrzej Żak
Department of Hydroacoustic and Radiolocation, Naval University of Gdynia, 81-103 Gdynia, Smidowicza 69, Poland
Keywords: Identification, MIMO Object, Dynamical System, Walsh Transform.
Abstract: The paper presents method of MIMO system identification using Walsh transform. Paper includes
description of mathematical basis of Walsh Transform. At the end of paper the results of research of
identification for example multi input multi output object were presented.
1 INTRODUCTION
Identification is very general notation which has
customary meaning in common speech. This
notation is variously defined dependently on
problem or science field but almost always is related
with creating the mathematical models of objects.
By the object’s model it is understood the
presentation of interested, essential properties in
convenient form. Therefore identification often
means the process in which results, basing on input
and output signals, arise the mathematical model of
object admitted as the best according to the accepted
criterions.
Procedure of identification can be, in the
simplest way, presented as it is done on figure 1.
Models appear in many fields of human
knowledge. They can be meet in physics, biology,
astronomy, technics, economy, sociology,
psychology and many others. For engineers
necessity of possession of models especially in
projection phase has no need to be contended. For
scientist models can be basis for wide research. In
all cases possession of models allow for preliminary
testing of creating systems what permits to
shortening the time necessary for projection phase
and inculcate of system. It also prevents from
accidental damage of real object.
Often modeling starts from apply some physical
laws which take part in investigated process. But it
is only possible when these phenomenons are quite
simple. If the numerical values of all external and
internal conditions of modeled object are known and
physical knowledge about this object is full it is
possible to calculate coefficients of all parameters.
However these cases are rare what become from
knowledge shortage about internal process and
indefinableness carried in by environment. In other
hand very often they are only interesting
dependences between object’s input and output
signals accepted that inputs signals are control
signals and measured output signals give
information about object state. In this case object
can treated as single or multi input and single or
multi output object but of unknown structure. In this
Figure 1: Schematic presentation of identification process
200
˙
Zak A. (2005).
WALSH TRANSFORM AS METHOD OF MIMO SYSTEMS IDENTIFICATION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 200-204
DOI: 10.5220/0001176302000204
Copyright
c
 SciTePress

time arise necessity to use identification or
estimation of process parameters to calculate
coefficients of models parameters. Values of this
parameters must be choose in such way so at
accepted mathematical structure will approximate
the behaviour of object in the best way according to
the accepted criterion. Because it is seldom possible
to calculate the precision values of model’s
parameters, it means the coefficients of
mathematical equations, the created model is only
some simplicity of reality but very often such
approximation is good enough.
2 WALSH TRANSFORM
Dynamical system can be considered as n-th
dimensional linear object which is described by
equation:
)()()(
1 kkk
TBuTAxTx
+
=
+
(1)
where:
)(
k
Tx
– state vector;
)(
k
– state matrix;
Tu
– control vector;
A
B
– control matrix;
k
T
– discreet time;
The main aim of identification is to calculate
matrixes
A
and knowing vector
B
x
and
u
.
Walsh function creates the family of binary,
orthogonal function which belongs to periodical
constant function. These functions are defined using
Rademacher function which can be written as:
⎪
⎩
⎪
⎨
⎧
−<≤
−
−
−<≤
−
+
=
++
++
oddi
i
t
i
for
eveni
i
t
i
for
tR
kk
kk
k
11
11
22
1
1
22
1
1
)(
(2)
where:
…,2,1,0=k
1
2,,2,1
+
=
k
i …
The relationship between Walsh function and
Rademacher function is as follow:
⎪
⎩
⎪
⎨
⎧
<≤=
<≤=
∏
=
10))(()(
101)(
0
0
tfortRtw
tfortw
n
i
n
kn
i
(3)
where:
…,2,1,0=n
i
- value of i-th position after conversion of n
into binary system.
n
The state vector and control vector can be
presented as orthogonal evolvement relative to
Walsh base function:
)()(
)()(
kHwTu
kFwTx
k
k
=
=
(4)
where:
)(kw
– k-th vector of discreet values of Walsh
function;
F
– matrix of coefficients of orthogonal
evolvement of state vector;
H
– matrix of coefficient of orthogonal
evolvement of control vector;
After bilateral summation of equation (1) and
substituted (4) we can receive the following
equation:
∑∑
+=−+
==
+
k
i
k
i
iiki
TBuTAxTxTxTx
00
01
))()(()()()(
The beginning vector
)(
0
Tx
can be written as
orth
(5)
ogonal evolvement relative to Walsh function
as:
)(]0,,0,0),([)(
00
kwTxTx …
=
(6)
Using pro Walsh transform that:
0
i
=
(7)
and
perties of
)()( kSwiw
k
=
∑
)()1( kZwkw
=
+
(8)
whe
g matrix for summarization of
re:
S
– operatin
Walsh functions;
Z
– operating matrix for shift of Walsh
nction;
the
fu
equation (5) can be written as:
)()()( kBHSwkAFSwkTw
+
=
(9)
whe
TxFZFS
re:
)(
0
T
−
+
=
.
On this equation only matrixes
A
and
B
which
are target of identification process are unknown and
matrixes and vectors are known. Getting
)( rn
rest of
+
-th random Walsh f ction is possible to
calculate all coefficients of
un it
A
and
B
matrixes what
ends the identification process.
WALSH TRANSFORM AS METHOD OF MIMO SYSTEMS IDENTIFICATION
201

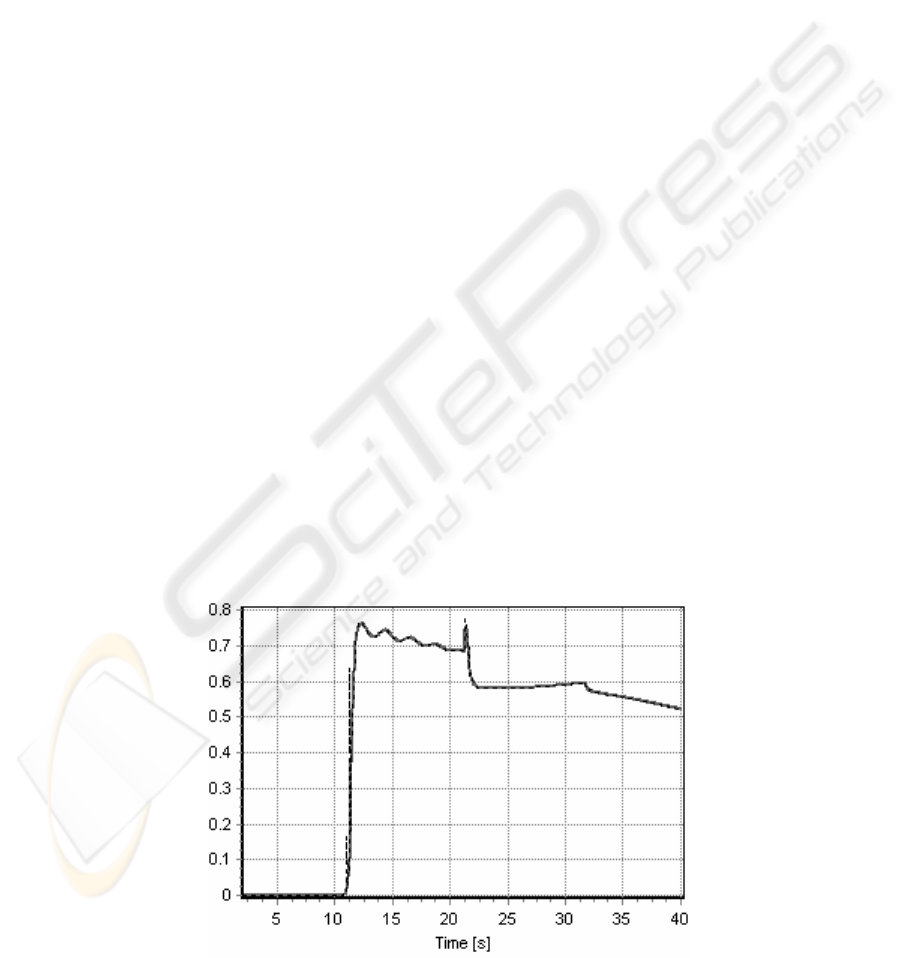
3 RESEARCH
Research was made on multi input multi output
dynamical object. This object was remotely operated
underwater vehicle type Ukwial which is equipment
of research unit of Naval University of Gdynia. The
precision mathematical model described by
nonlinear equations of this object is know and was
created during experimental measurements. The
target of identification process was to present this
object according to the equation (1). It can be done
by calculating the coefficients of state matrix and
control matrix. These matrixes were calculated using
presented above method of Walsh transform.
First step was to collect the measurements of
control vector and state vector. Next step was to
basis on matrix of randomly chosen Walsh function
and measured control vectors and state vectors
calculate the ort nt of all these
rol vector was also
to Walsh function.
Next the matrix:
WT
′
= ))(
⎡
=
WFS
Q
because the matrix
include state matrix
in its first
n
-th rows where
n
is a length of state
vector and include contro
(
hogonal evolveme
vectors. Then the beginning cont
orthogonal evolvement relative
TxFZFS
−+ (
0
was calculated. Now the matrix:
⎥
⎤
′
⎦
⎣
′
WHS
was created. Basis on this matrixes the matrix
1−
= TQR
was calculated. The last step was to separate the
coefficients e matrix nd control matrix. It can
be done
⎢
of stat a
R
l matrix in rows from
)1
+
n
to
)( rn
+
where
r
is the length of control
vector.
The basement for calculation was state vector of
this object whic
respectively;
at log for linear speeds
me
meter.
The control vector for th object can be written
as follow:
h can be written as:
],,,,,[ rqpwvu
where:
],,[ wvu
– surge, sway, heave velocity
],,[ rqp
– roll, pitch, yaw velocity respectively.
These parameters described object movement are
possibilities to measure because this object is by
standards equipped
asurements, electric compass and electrolytic
inclination-
is
],,[
zyx
τ
τ
τ
where:
zyx
τ
τ
τ
,,
– set forces of propeller in
z
y
x
,,
dire
ifference
bet
seconds it takes
become to
]0,220,220[
and on the
end
object
(solid, gray line) and calculated by identification
process (doted, black line) were presented.
ction.
The criterion of opinion was the d
ween state vector generated by object and
calculated b ification procedure.
During research the control vector at start point
has value
]0,0,0[
. After ele
value
]0,0,220[
. Next in twenty first seconds the
has
y ident
ven
control vector
after thirty one seconds it takes values of
]220,220,220[
.
Below on figures 2 to 7 the graphs of change of
every component of state vector generated by
Figure 2: Changes of surge velocity generated by object and identified values
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
202

Figure 3: Changes of sway velocity generated by object and identified values.
Figure 4: Changes of heave velocity generated by object and identified values
Figure 5: Changes of roll velocity generated by object and identified values
WALSH TRANSFORM AS METHOD OF MIMO SYSTEMS IDENTIFICATION
203

Figure 6: Changes of pitch velocity generated by object and identified values
Figure 7: Changes of yaw velocity generated by object and identified values
4 CONCLUSION
As it is shown in research the Walsh transform is
useful to identify dynamics of multi input, multi
output object. Because of some limitation this
method can be used to identify dynamics of objects
which state vector is slow changed. In case of object
with fast changed state vector presented method
can’t calculate actual answer on time. This method is
perceive as promise to practical use because of
simplify of implementation on digital machine and
flexibility of use.
Feature research will concentrated on optimal
selection of Walsh transform length and on using
this method to identify state vector of various
dynamical object in control processes.
REFERENCES
Fossen Thor I., 1994. Guidance and control of ocean
vehicles, John Wiley & Sons, Chichester
Garus J., 1993. Identification of moving objects
parameters in exploational conditions using numerical
methods, AMW, Gdynia
Eykhoff P., 1980. Identification in dynamical systems,
PWN, Warszawa
Mańczak K., 1979. Methods of identification of multi-
dimensional control objects, PWN, Warszawa
Mańczak K., Nahorski Z., 1983. Computer identification
of dynamical objects, PWN, Warszawa
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
204