
COOPERATIVE SELF-ORGANIZATION
TO DESIGN ROBUST AND ADAPTIVE COLLECTIVES
Gauthier Picard and Marie-Pierre Gleizes
IRIT - Université Paul Sabatier
118, route de Narbonne - 31062 Toulouse Cedex FRANCE
Keywords:
Multi-agent systems, Cooperation, Self-organization.
Abstract:
This paper highlights the benefits of using cooperation as the engine of adaptation and robustness for multi-
agent systems. Our work is based on the AMAS (Adaptive Multi-Agent System) approach which considers co-
operation as a self-organization mechanism to obtain adequate emergent global behaviors for systems coupled
with complex and dynamic environments. A multi-robot resource transportation task illustrates the instanti-
ation of a cooperative agent model equipped with both reactive and anticipative cooperation rules. Various
experiments underline the relevance of this approach in difficult static or dynamic environments.
1 INTRODUCTION
To provide a self-organizing collective behavior, the
parts composing a system need a local criterion to
re-organize so as to provide a more adapted function
(Heylighen, 1999). Designers must specify this crite-
rion and equip parts to process and handle this crite-
rion. To the first point, the AMAS approach answers
by using an artificial socially inspired notion, close to
symbiosis (Maturana and Varela, 1994): cooperation
(Capera et al., 2003). The second point is fulfilled by
using an autonomic agent approach, which provides
decision-making capabilities to parts. Cooperative
agents aim at avoiding Non Cooperative Situations
(NCS) as a generic proscriptive re-organizational rule.
The advantage of the AMAS approach is to ensure, by
providing adequate cooperative local behaviors, that
the collective will provide the adequate and adapted
global function. To design such agents, a coopera-
tive agent model is available in the ADELFE method
(Bernon et al., 2003). To highlight the relevance of
using the cooperative agent model, we propose to de-
velop a multi-robot resource transportation task, in
which several similar robots have to transport boxes
from a room to another one, by passing through nar-
row corridors, which produce spatial interferences.
This paper rather focuses on the ability of a system
to react to environmental changes and on the observa-
tion of emergent phenomena, rather than on the nomi-
nal efficiency of the transport task. Section 2 presents
the agents of the system –the robots– by developing
their different modules and nominal behaviors. Sec-
tion 3 explains the different cooperation rules robots
have to respect to achieve their goals in a more effi-
cient way. An experiment platform has been devel-
oped to test the instantiation of the cooperative agent
model. Several results are expounded and discussed
in section 4 before concluding.
2 COOPERATIVE ROBOT
AGENTS
By using the ADELFE method, robots are described
with several modules which represent a partition
of their physical, social and cognitive capabilities
(Bernon et al., 2003).
The Perceptions Module represents inputs for
agents: position of the claim zone, position of the lay-
ing zone, a limited perception cone in which objects
(robot, box or wall) are differentiable, proximity sen-
sors (forward, backward, left and right), a compass
and the absolute spatial position. The environment
is discretized as a grid whose cells represent atomic
parts on which an object can be situated.
The Actions Module represents outputs from the
agents on their environment. Actions for the trans-
porter robots are: rest, pick, drop, forward, backward,
left and right. Robots cannot drop boxes anywhere
in the environment but only in the laying zone. They
cannot directly communicate or drop land marks on
the environment.
The Skills Module contains knowledge about the
task the agent must perform. Skills enable robots to
achieve their transportation goals. Therefore, a robot
is able to calculate which goal it must achieve in terms
of its current state: if it carries a box then it mustreach
236
Picard G. and Gleizes M. (2005).
COOPERATIVE SELF-ORGANIZATION TO DESIGN ROBUST AND ADAPTIVE COLLECTIVES.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 236-241
DOI: 10.5220/0001177902360241
Copyright
c
SciTePress
laying zone else it must reach claim zone. As a func-
tion of its current goal, the Skills Module provides an
action to process to achieve it. Moreover, robots have
intrinsic physical characteristics such as their speed,
the number of transportable boxes or the preference
to move forward rather than backward – as ants have.
Such preferences are called reflex values (see 2.2).
The Representations Module contains knowledge
about the environment (physical or social). The rep-
resentations a robot has on its environment are very
limited. From its perceptions, it cannot distinguish a
robot from another one, but can know if it is carrying
a box or not. It also can memorize its past absolute
position, direction, goal and action.
The Aptitudes Module enables an agent to choose
an action in terms of its perceptions, skills and rep-
resentations. In terms of the current goal, the Skills
Module provides preferences on every action the ro-
bot may do. The Aptitudes Module chooses among
these actions what will be the next action to reach
the goal. Many decision functions can be considered;
e.g. an arbitrary policy (the action having the high-
est preference is chosen) or a Monte Carlo method-
based policy, which is chosen for our example, since
it has already been successfully applied to foraging
tasks (Topin et al., 1999). Therefore, the Aptitudes
Modules can be summed up in a Monte Carlo deci-
sion function on the preference vector (the list of ac-
tion preferences for an agent) provided by the Skills
Module. In the same manner, the Cooperation Mod-
ule provides preference vectors in order to solve the
NCS which are described in section 3.
2.1 Internal Functioning
During the perception phase of the agents’ life cycle,
the Perceptions Module updates the values of the sen-
sors, which directly implies changes in the Skills and
Representations Modules. Once the knowledge is up-
dated, the decision phase results in an action choice.
During this phase, the Aptitudes Module computes
from knowledge and proposes action(s) or not. At
each time t, a robot chooses between different actions
that are proposed by the two decision modules (Skills
and Cooperation). At time t, each action act
j
of the
robot r
i
is evaluated. For each action, this value is cal-
culated in terms of perceptions, representations and
reflexes in the case of a nominal behavior:
V
nomi
r
i
(act
j
, t) =wp
r
i
(act
j
, t) + wm
r
i
(act
j
, t)+
wr
r
i
(act
j
)
with:
• V
nomi
r
i
(act
j
, t) represents the value for the action
act
j
at time t for the robot r
i
,
• w p
r
i
(act
j
, t) represents the calculated value in
terms of perceptions,
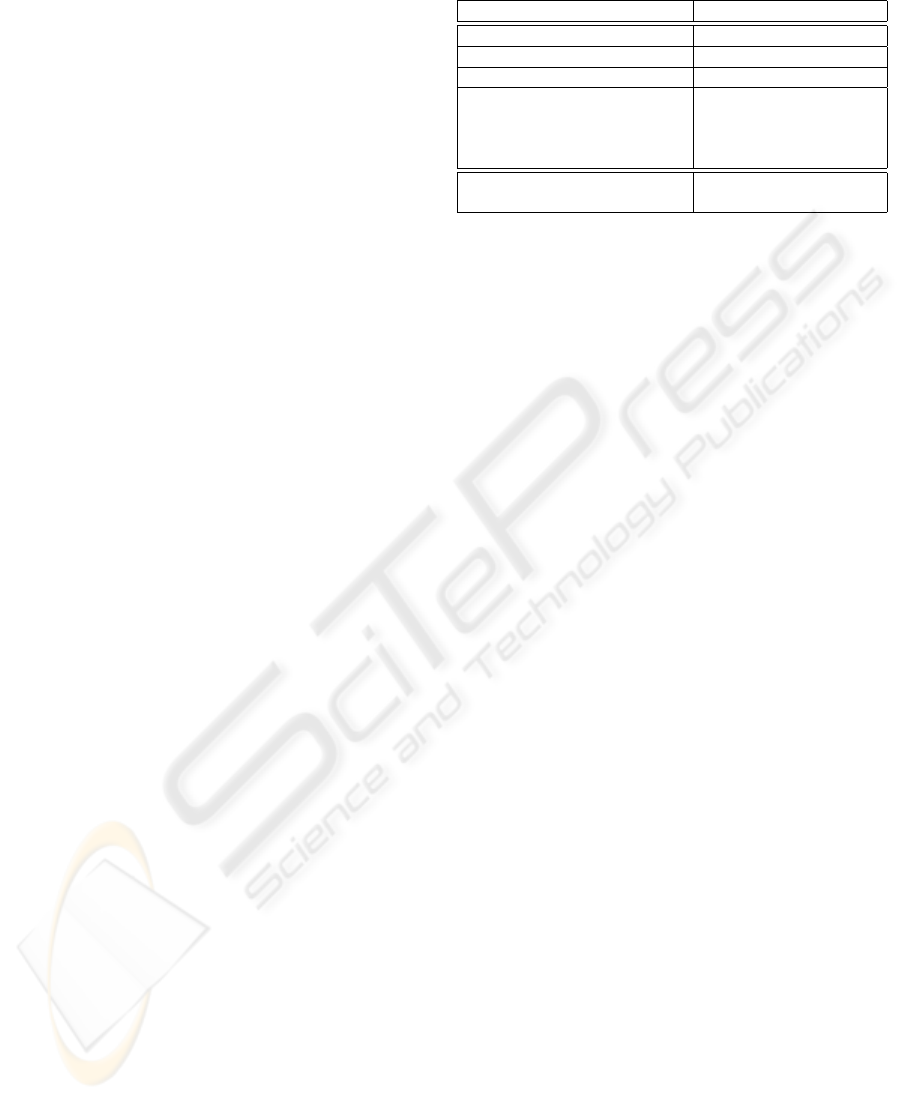
Table 1: Specification of the nominal behavior
Perceptions Effects
¬car ∧ cBox ր wp
r
i
(pick, t)
¬car ∧ ¬cBox ∧ sBox ր wp
r
i
(forward, t)
¬car∧¬cBox∧ ¬ sBox∧¬inCZ ր wp
r
i
(hCZdiri, t)
¬car ∧ ¬cBox ∧ ¬sBox ∧ inCZ ր wp
r
i
(backward, t)
ր wp
r
i
(forward, t)
ր wp
r
i
(lef t, t)
ր wp
r
i
(right, t)
car ∧ cLZ ր wp
r
i
(drop, t)
car ∧ ¬cLZ ր wp
r
i
(hLZdiri, t)
with:
• car: r
i
is carrying a box,
• cBox: r
i
is close to a box,
• sBox: r
i
is seeing a box,
• inCZ: r
i
is in the claim zone,
• cLZ: r
i
is close to the laying zone,
• cLZ: r
i
is close to the laying zone,
• hCZdiri: the move to perform to go to claim zone,
• hLZdiri: the move to perform to go to laying zone,
• ր: increasing.
• w m
r
i
(act
j
, t) represents the calculated value in
terms of memory,
• w r
r
i
(act
j
, t) represents the calculated value in
terms of reflexes.
All the V
nomi
r
i
(act
j
, t) are grouped in a vector,
called action preference vector. In the same manner,
the Cooperation Module detects if the agent is faced
up to a NCS or not. In the former case, the Coop-
eration Module proposes an action that subsumes the
actions proposed by the Aptitudes Module. In the lat-
ter case, the action proposed by the Aptitudes Module
is chosen and, then, the agent acts by activating effec-
tors and/or changing its knowledge. As for aptitudes,
an action preference vector, V
coop
r
i
(act
j
, t), is gener-
ated by the Cooperation Module, by regrouping eval-
uation of the actions. Once these values have been
calculated by the two modules for each action of a ro-
bot, the vector on which the Monte Carlo drawing will
process is a combination of the two vectors in which
the cooperation vector subsumes the nominal vector:
V
r
i
(t) = V
nomi
r
i
(t) ≺ V
coop
r
i
(t)
2.2 Nominal Behavior
The nominal behavior is described with rules that
modify the values in the V
nomi
preference vec-
tor. This vector is obtained by adding values from
perceptions (wp
r
i
(act
j
, t)) and values from reflexes
(wr
r
i
(act
j
, t)). Memory is not necessary to imple-
ment a this behavior. Table 1 shows values to increase
in the wp
r
i
(act
j
, t) to achieve the two disjoint goals:
reach claim zone (¬car) and reach laying zone (car).
Reflex values are static and also depend on percep-
tions and more precisely on the direction of the ro-
bot. As for ants, robots may prefer moving forward
COOPERATIVE SELF-ORGANIZATION TO DESIGN ROBUST AND ADAPTIVE COLLECTIVES
237

then backward (Topin et al., 1999). For example, val-
ues for wr
r
i
(act
j
, t) can be: wr
r
i
(forward, t) =
50; wr
r
i
(lef t, t) = 10; wr
r
i
(right, t) = 10;
wr
r
i
(backward, t) = 0. Thus, even if a goal leads
a robot to a wall, the robot can move by side, as ants
do to forage and to avoid dead ends. But, this mech-
anism is not sufficient to avoid deadlocks in long nar-
row corridors in which robots cannot cross. The goal
is more influential than reflexes. As a consequence,
defining cooperation rules is necessary to enable all
robots to achieve their tasks without deadlock.
2.3 Cooperative Attitude of Agents
The AMAS theory identifies several types of NCS
(Capera et al., 2003), resulting from the analysis of
the cooperation definition which is close to the sym-
biosis notion. An agent is cooperative if: all perceived
signals are understood without ambiguity (c
per
) and
the received information is useful for the agent’s rea-
soning (c
dec
) and reasoning leads to useful actions to-
ward other agents (c
act
). Therefore, a NCS occurs
when ¬c
per
∨ ¬c
dec
∨ ¬c
act
. We identify seven NCS
subtypes that express these conditions:
• incomprehension (¬c
per
): the agent cannot extract
the semantic contents of a received stimulus,
• ambiguity (¬c
per
): the agent extracts several inter-
pretations from a same stimulus,
• incompetence (¬c
dec
): the agent cannot benefit
from the current knowledge state during the deci-
sion,
• unproductiveness (¬c
dec
): the agent cannot pro-
pose an action to do during the decision,
• concurrency (¬c
act
): the agent perceives another
agent which is acting to reach the same world state,
• conflict (¬c
act
): the agent believes the transforma-
tion it is going to operate on the world is incompat-
ible with the activity of another agent,
• uselessness (¬c
act
): the agent believes its action
cannot change the world state or it believes results
for its action are not interesting for the other agents.
Cooperative agents must avoid or repair these NCS,
if they occur. Designing such agents focuses on NCS
specification –a kind of exception-oriented program-
ming in which designers focus on exceptions.
3 COOPERATIVE
SELF-ORGANIZATION
Beyond two robots, acting to transport boxes in a
same environment, the nominal behavior is no more
adequate. Indeed, a robot is equipped with skills to
achieve its tasks, but not to work with other robots. In
a constrained environment, spatial interference zones
appear. If two robots, a first one carrying a box and
moving to the laying zone and a second one moving
to the claim zone to pick up a box, meet in a corridor,
the circulation is blocked.
3.1 Reactive Cooperation
Two main NCS can be reactively solved, without re-
quiring memory:
A robot is blocked. A robot r
1
cannot move for-
ward because it is in front of a wall or another ro-
bot r
2
moving in the opposite direction
1
. In this
case, if it is possible, r
1
must move to its sides (left
or right). This corresponds to increasing values of
the cooperative action vector related to side move-
ments: V
coop
r
1
(t, right) and V
coop
r
1
(t, lef t). If r
1
can-
not laterally move, two other solutions are openned.
If r
2
has an antagonist goal, the robot which is the
most distant from its goal will move backward (in-
creasing V
coop
r
i
(t, backward)) to free the way for
the robot which is the closest to its goal (increasing
V
coop
r
i
(t, forward) even if it may wait). Robots can
evaluate which is the most distant since they know
their goals and the associated zones. If r
2
has the
same goal than r
1
, except if r
1
is followed by an an-
tagonist robot or if r
1
moves away from its goal (vis-
ibly it moves to a risky
2
region), r
1
moves backward;
else r
1
moves forward and r
2
moves backward.
A robot is returning. A robot r
1
is returning
3
as
a consequence of a traffic blockage. If it is possible,
r
1
moves to its sides (and is not returning anymore).
Else, r
1
moves forward until it cannot continue or if it
encounters another robot r
2
which is returning and is
closer to its goal than r
1
. Table 2 sums up the cooper-
ative behavior in this situation. If there is a queue of
robots, the first returning robot is seen by the second
one that will return too. Therefore, the third one will
return too and so on until there are no more obstacles.
These two rules correspond to resource conflicts
(on corridors) or uselessness (when robots move
backward and away from their goal) situations. These
rules, which are simple to express, ensure that robots
cannot block each other in corridors, and robots do
not need to communicate. But, this cooperative atti-
tude only solves problem instantly, creating returning
movements and then implying time loss.
1
If r
2
moves in another direction than the opposite di-
rection of r
1
, it is not considered as blocking because it will
not block the traffic anymore on the next step.
2
It is risky in the sense it may lead to the occurrence of
a lot of non cooperative situations such as conflicts.
3
A robot is considered as returning while it has no
choice of side movements.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
238

Table 2: Specification of "a-robot-is-returning" NCS.
Condition Action
ret ∧ f R ր V
coop
r
i
(t, right)
ret ∧ f L ր V
coop
r
i
(t, left)
ret∧¬(f L∨ f R)∧ant∧toGoal∧
cGoal
ր V
coop
r
i
(t, backward)
ret∧¬(f L∨ f R)∧ant∧toGoal∧
¬cGoal
ր V
coop
r
i
(t, f orward)
ret∧ ¬(fL∨fR)∧ant∧¬toGoal ր V
coop
r
i
(t, backward)
ret ∧ ¬(f L ∨ f R) ∧ ¬ant ր V
coop
r
i
(t, f orward)
with:
• ret: r
i
is returning,
• fR: right cell is free,
• fL: left cell is free,
• ant: in front of an antinomic robot,
• toGoal: r
i
is moving to goal,
• cGoal: r
i
is closer to its goal than its opposite one,
• ր: increasing.
3.2 Anticipative Cooperation
It is possible to specify cooperation rules to antici-
pate blockage situations in order to make the collec-
tive more efficient : these rules are optimization coop-
eration rules. Previous rules enable robots to extract
from blockage. A robot is in such a situation because
it was crossing a zone frequented by antinomic robots.
So as to prevent this situation and to avoid repeating
their past non cooperation failures, robots must mem-
orize locations of risky areas (from which antinomic
robots come) and avoid them. Thus, an anticipation
rule can be specified:
A robot sees an antinomic robot. If a robot r
1
per-
ceives a robot r
2
having an antinomic goal and if r
1
can move to its sides it does else it moves forward.
Nevertheless, this reactive anticipation presents
a major problem: once a robot has avoided the
risky zone, no mechanism ensures that it will not
go in it again, led by its goal. Robots can be
equipped with a limited memory of the risky zones
(in the Representations Module). Each time t a
robot r
i
experiments an anticipation situation fac-
ing a robot r
j
, it memorizes a tuple (or virtual
marker) hposX(r
j
, t), posY (r
j
, t), goal(r
i
, t), wi in
which posX(r
i
, t) and posY (r
i
, t) represent the co-
ordinates of r
j
at the moment t. goal(r
i
, t) repre-
sents the goal r
i
was achieving at time t. w repre-
sents a repulsion value. The higher this value is, the
more the robot will try to avoid the zone described
by the marker when it is achieving another goal than
goal(r
i
, t). Therefore, the robot inspects all its per-
sonal markerswhose distance is less than its percep-
tion limit (to fulfill the locality principle). A marker
with a weight w and situated in the direction dir at
a distance d induces that V
coop
r
i
(t, dir
opp
) will be in-
creased of w (dir
opp
is the opposite direction to dir).
As the memory is limited, tuples that are added
Figure 1: Average number of returned boxes in terms of
simulation time and standard deviation for 15 simulations
for different behaviors: individualist, cooperative unblock-
ing, cooperative anticipative and hardcoded behavior.
must disappear at runtime. The weight w decreases
of a given value δ
w
(called forgetting factor) at each
step. Once w = 0, the tuple is removed from the
memory. This method corresponds to the use of vir-
tual and personal pheromones, and, as ants do, robots
reinforce their markers: a robot moving to a position
corresponding to one of its marker with another goal,
re-initializes the marker. But contrary to the ant ap-
proach, no stigmergy or physical medium are needed.
4 EXPERIMENTS AND
DISCUSSION
The expounded model has been implemented and
simulated in the environments shown in figures 3, 4
and 5, with the different entities : boxes (non bordered
circles), robots without boxes (light grey bordered cir-
cles) and robots carrying boxes (dark grey bordered
circles). This environment is made up of two rooms
(25 × 30 cells) separated by two long and narrow cor-
ridors (30 × 1 cells). 300 robots are randomly placed
in the claim room. These robots can perceive at a dis-
tance of 5 cells, and can make a move of one cell at
each step. If they can anticipate conflicts, their mem-
ory can contain 1500 tuples with an initial repulsion
value w = 400 and a decrease value δ
w
= 1.
Reaction vs. Anticipation. Figure 1 shows a com-
parison between the average numbers of transported
boxes for 15 simulations (300 robots, 2 corridors, 5-
ranged perception), corresponding to the nominal be-
havior (individualist), a hardcoded one and two co-
operative ones: the cooperative unblocking behavior
(see section 3.1) and the cooperative anticipative be-
havior (see section 3.2). By adding blockage antici-
pation, the collective becomes more efficient (at least
30% more boxes are transported). According to the
AMAS paradigm, we can experimentally observe that
the local resorption of NCS leads to the collective
functional adequacy. Nevertheless, equipping agents
COOPERATIVE SELF-ORGANIZATION TO DESIGN ROBUST AND ADAPTIVE COLLECTIVES
239

0
2000
4000
6000
8000
10000
12000
14000
16000
18000
20000
0 20000 40000 60000 80000 100000
Steps
Robots
Moving to claim zone
Moving to laying zone
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
20000
0 20000 40000 60000 80000 100000
Steps
Robots
Moving to claim zone
Moving to laying zone
Figure 2: Incoming robots for the top corridor for two dif-
ferent behaviors: unblocking behavior (left) and anticipa-
tive unblocking behavior (right).
Figure 3: Positioning of all the virtual markers (dark
squares) for all the robots and the two goals.
with cooperative behavior is not as efficient as hard-
coding by giving non adaptive passage points: claim
zone, then corridor 1, then laying zone, then corridor
2, as shown in figure 1. Finally, the global adaptive
behavior is not sensible to initial state as shown by
the standard deviation, which is negligible.
Emergence of Corridor Dedication. Figure 2
shows the corridor-usage for the two cooperative be-
haviors, i.e. the number of incoming robots for a cor-
ridor and for the two cooperative behaviors: unblock-
ing behavior (left) and anticipative unblocking behav-
ior (right). In the case of anticipative behavior, we can
observe the emergence of a sense of traffic. Robots
collectively dedicate corridors to particular goals. In
fact, markers of all the agents are positioned only at
one corridor entry for one direction as shown in figure
3. This view is only for monitoring purpose: robots
do not perceives all the markers, only their owns. We
can assign the emergent property to this phenomenon
because robots do not handle any notion of corridor
– unlike some previous works (Picard and Gleizes,
2002). Thus, just with local data, robots established a
coherent traffic behavior that leads to an optimization
of the number of transported boxes.
Robustness in Difficult Environments. Some sim-
ulations have been done in the environment with dead
ends of figure 4. Robots are able to manage such
difficulties by using directions at a higher abstraction
level. For example, the forward direction is not sim-
ply interpreted as going straight forward. If the robot
has only one free direction, left for example, going
Figure 4: Positioning of all the virtual markers (dark
squares) for the goal reach laying zone in a difficult envi-
ronment (with deadends).
Figure 5: Positioning of the virtual markers (dark squares)
in a dynamic environment with two closed corridors.
forward will become going left. As a consequence,
a dead end problem is easily avoided. But, robots
do not distinguish corridors, since they are too close
and markers are not precise enough. In our exam-
ple, corridors are separated by only 9 cells, which
is less then two times the perception distance of ro-
bots. Therefore, marked areas intersect and robots
cannot precisely detect which corridor to avoid. Thus,
there is no corridor dedication, as shown in figures 4.
However, the collective behavior is robust enough so
that no deadlock appears, even if the collective be-
comes less efficient, because the learning process is
disabled. Solving this problem implies either mod-
ifying parameters such as distance of perception or
repulsing force of markers in function of the envi-
ronment (which is too environment-dependent), or
adding learning capabilities on these parameters by
adding new NCS rules.
Adaptation to Dynamics. Simulations have been
done with an environment with four corridors. At
each 10,000 step period, two corridors are randomly
chosen and closed to add non determinism and dy-
namics. Here again, the collective is less efficient, but
there is no deadlock. Of course, if corridor closing
is too frequent, robots cannot adapt and dedicate di-
rections to corridors. In fact, 300 robots need about
2000 steps to adapt. Figure 5 shows that only entries
of opened corridors are marked and some robots can
be captured in closed corridors, and are then useless.
During each closing period, the two opened corridors
are exploited and a direction is affected. Moreover,
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
240

Figure 6: Compared efficiency (boxes/time) between a sim-
ulation in a static environment with two corridors and an-
other one in an dynamic environment with 4 corridors
which 2 corridors are randomly closed every 10,000 steps.
the effect of the environmental dynamic become neg-
ligible with a great number of steps. Figure 6 shows
the efficiency for two different environment (static or
dynamic). The efficiency of the system in the static
one is more stable but equivalent to the efficiency of
the system which evolves in the dynamic one.
Discussion. The AMAS cooperative agent ap-
proach is relevant for several reasons. Firstly, unlike
ant algorithms (Bonabeau et al., 1997), robots do not
physically mark their environment with pheromones,
but memorize personal markers. Secondly, contrary
to competition-based (Vaughan et al., 2000) or altruis-
tic (Lucidarme et al., 2002) approaches, robots do not
need direct communication to inform close robots or
exchange requests and intentions. Thirdly, coopera-
tive behavior encoding is insensitive to the number of
robots, to the topography and to the dimensions of the
environment. Fourthly, no global feedback is needed
to lead the system to functional adequacy, which pre-
vents the system to reach local extrema. Finally, ob-
tained collectives are robust and adaptive, even if per-
ception capabilities are very limited. Nevertheless,
ADELFE does not provide any guidance to instan-
tiate these values. For instance, the initial weights
for markers and the forgetting factor have been ad-
justed to the time robots spend to cross the entire
environment. This might be completely different in
a more complex environment with more or less cor-
ridors which can dynamically open or close. Some
simulations have been done with such environments,
and the affected values seem correct unless corridors
are too close to each other or frequency of closure is
too fast. These values also may be learnt at runtime,
which is one of our perspectives.
5 CONCLUSION
In this paper, we have shown the relevance of co-
operation as a local criterion for collectives to self-
organize to be more adapted to a specific task. Con-
sidering the ignorance of the global task and the
environment, the self-organizing collective reaches
an emergent coherent behavior, which is then more
robust to environmental risks. Our simulation ap-
plication tackles a simple problem in a simple sta-
tic environment in which the collective achieves its
global task. Simulations in difficult and dynamic en-
vironments confirm the relevance of cooperative self-
organizing collectives. Finally, this application has
been developed to confront the ADELFE cooperative
agent model to a task that requires adaptation and ro-
bustness. However, this application is very specific,
in the sense it only concerns quasi-reactive non com-
municative robots. In the case of agents able of com-
municative acts, other kinds of NCS are possible.
REFERENCES
Bernon, C., Camps, V., Gleizes, M.-P., and Picard, G.
(2003). Designing Agents’ Behaviors and Interac-
tions within the Framework of ADELFE Method-
ology. In 4
th
Engineering Societies in the Agents
World (ESAW’03), volume LNCS 3071, pages 311–
327. Springer-Verlag.
Bonabeau, E., Theraulaz, G., Deneubourg, J.-L., Aron, S.,
and Camazine, S. (1997). Self-organization in social
insects. Trends in Ecology and Evolution, 12:188–
193.
Capera, D., Georgé, J., Gleizes, M.-P., and Glize, P. (2003).
The AMAS theory for complex problem solving based
on self-organizing cooperative agents. In 1
st
Int.
TAPOCS Workshop at 12
th
IEEE WETICE, pages
383–388. IEEE.
Heylighen, F. (1999). The Science of Self-organization and
Adaptivity. EOLSS Publishers.
Lucidarme, P., Simonin, O., and Liégeois, A. (2002). Imple-
mentation and Evaluation of a Satisfaction/Altruism
Based Architecture for Multi-Robot Systems. In IEEE
Int. Conf. on Robotics and Automation (ICRA’02),
pages 1007–1012.
Maturana, H. and Varela, F. (1994). The Tree of Knowledge.
Addison-Wesley.
Picard, G. and Gleizes, M.-P. (2002). An Agent Architec-
ture to Design Self-Organizing Collectives: Principles
and Application. In AISB’02 Symposium on Adaptive
Multi-Agent Systems (AAMASII), volume LNAI 2636,
pages 141–158. Springer-Verlag.
Topin, X., Fourcassié, V., Gleizes, M.-P., Theraulaz, G.,
Régis, C., and Glize, P. (1999). Theories and experi-
ments on emergent behaviour : From natural to artifi-
cial systems and back. In European Conf. on Cogni-
tive Science, Siena, Italy.
Vaughan, R., Støy, K., Sukhatme, G., and Matari
´
c, M.
(2000). Go ahead make my day: Robot conflict reso-
lution by aggressive competition. In 6
th
Int. Conf. on
Simulation of Adaptive Behaviour.
COOPERATIVE SELF-ORGANIZATION TO DESIGN ROBUST AND ADAPTIVE COLLECTIVES
241
