A PARAMETERIZED POLYHEDRA APPROACH FOR THE

EXPLICIT ROBUST MODEL PREDICTIVE CONTROL

Sorin Olaru

Supelec

3 rue Joliot Curie, Gif-sur-Yvette, France

Didier Dumur

Supelec

3 rue Joliot Curie, Gif-sur-Yvette, France

Keywords:

Predictive control, constraints, parameterized polyhedra, multiparametric optimization.

Abstract:

The paper considers the discrete-time linear time-invariant systems affected by input disturbances. The goal is

to construct the robust model predictive control (RMPC) law taking into account the constraints existence from

the design stage. The explicit formulation of the controller is found by exploiting the fact that the optimum of

a min-max multi-parametric program is placed on the parameterized vertices of a parameterized polyhedron.

As these vertices have speciﬁc validity domains, the control law has the form of a piecewise linear function of

the current state. Its evaluation replaces the time-consuming on-line optimization problems.

1 INTRODUCTION

Model Predictive Control (MPC) enjoys a remarkable

reputation among the control design techniques for

process industries. In the beginnings, practitioners

used MPC in the unconstrained closed forms due to

its simplicity and versatility and dealt with the con-

straints violation a posteriori. In the ’90s, theoreti-

cians proved that constraints could be included at the

design stage with excellent results towards the fea-

sibility, stability or robustness. The inconvenience,

which represented also an impasse in applying the

constrained predictive control to high sampling rate

systems, was the relative high complexity of the op-

timization problem to be solved at each sampling pe-

riod. Lately, the constrained MPC paradigm was re-

formulated in terms of LMI (Kothare et al., 1996)

with a reduction of computational time but the class

of system to be controlled was still limited.

An improvement from the on-line computational

point of view can be achieved if the explicit solution

of the MPC optimization problem is formulated. In

this way, at each sampling time, a piecewise linear

function has to be evaluated. In fact the MPC strat-

egy is based on a multi-parametric optimization prob-

lem as both the global optimum and the set of con-

straints are parameter dependent. In the nominal case

corresponding with a quadratic optimization problem

and linear constraints, the explicit solution was inves-

tigated with success using an algebraic approach in

(Bemporad et al., 2002b), geometrical arguments in

(Seron et al., 2002), (Olaru and Dumur, 2004) and

lately dynamic programming (Goodwin et al., 2004).

In the case of robust MPC, the explicit solution is

somehow more difﬁcult to achieve as the optimization

problem is based on a min-max cost function. It was

successfully tackled in (Bemporad et al., 2001) but

the alternative methods do not present similar solu-

tions so far. The current work is trying to compensate

this setback through an explicit solution for the ro-

bust MPC by geometrical base. The method is based

on the concept of parameterized polyhedra (Loechner

and Wilde, 1997) and their correspondent parameter-

ized vertices where the optimal solution is founded.

2 ROBUST MPC FORMULATION

Consider the MPC problem formulated for a discrete-

time linear time-invariant system affected by an input

disturbance:

t+1

= Ax

+ Bu

+ Ev

(1)

and subject to a set of linear constraints:

+ D u

≤ d (2)

The vectors x

∈ R

and u

∈ R

represent the

states and inputs while v

∈ R

is the unknown vector

of disturbances lying inside a polytope containing the

Olaru S. and Dumur D. (2005).

A PARAMETERIZED POLYHEDRA APPROACH FOR THE EXPLICIT ROBUST MODEL PREDICTIVE CONTROL.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 3-10

DOI: 10.5220/0001178400030010

 SciTePress

origin deﬁned by a set of linear constraints:

V = {v |Mv 6 l; l > 0} (3)

In the following, the pair (A, B) is supposed to be sta-

bilizable and it is assumed that the full measurement

of the current state is available at each time t.

MPC is an optimization based technique. In oppo-

sition to the nominal case where quadratic cost func-

tions are used (Maciejowski, 2002), (Rossiter, 2003),

in the case of models affected by disturbance, a min-

max optimization is preferred, resulting a RMPC for-

mulation:

min

,...,u

t+N

−1



max

,...,v

t+N−1



t+N|t

N−1

k=1



t+k|t



∞

−1

k=0

kRu

t+k

∞

))

(4)

s.t.: Cx

t+k|t

+ D u

t+k

6 d, k = 1, . . . , N

t+k

6 l, k = 0, . . . N − 1

t+k+1|t

= Ax

t+k|t

+ Bu

t+k

+ Ev

t+k

k > 0, x

t+N|t

∈ P

(5)

with Q, R weighting matrices,k∗k

∞

max

i=1,...,r



∗



, where ∗

is the i-th element

of the vector ∗ ∈ R

. The state predictions x

t+k|t

are obtained based on the current state vector x

and

by applying the input sequence u

, . . . , u

t+Nu−1

, to

model (1) over a control horizon. Note that, in the

general case, the control (N

) and the prediction (N )

horizons might be different if the control vector has

a ﬁx formulation for N

6 k 6 N. Conversely,

the disturbance sequence v

, . . . , v

t+N−1

affects the

prediction over the whole prediction horizon.

The stability of the MPC scheme depends on the

chosen horizons and on the terminal cost. In order to

guarantee the stability, an inﬁnite prediction horizon

should be used. Such a choice transforms (4)-(5) in an

intractable problem. The solution is then to choose a

ﬁnite prediction horizon and to consider that after this

point the system trajectory is brought inside a posi-

tively invariant set, P , that can be computed off-line

(Kerrigan, 2000). To this terminal region a function

(x) can be associated, appearing in (4) as a termi-

nal cost penalizing the evolution from N to ∞.

Applying a receding horizon strategy the optimiza-

tion (4)-(5) is solved at each sampling time t us-

ing the measured state vector x

(playing the role

of parameter for the optimization). If k

∗

) =



∗

, . . . , u

∗

t+N

−1



is the solution to (4)-(5), the in-

put applied to the system (1) is the ﬁrst value of this

sequence k

∗

) such that u

= u

∗

, the other values

are abandoned and the procedure is restarted.

A special concern must be given to the choice of the

control horizon. Indeed, this parameter is sensitive

as it reﬂects the number of degrees of freedom avail-

able to ensure the constraints fulﬁllment for all possi-

ble combinations of disturbances. On the other hand,

with less control alternatives the computational load

is diminished. In the robust MPC case, the control

horizon is generally equal with the prediction horizon

= N , as the cumulative effect of the worst case

disturbances needs an important control counterpart.

min

max

min

t+1

. . . min

t+N

−1

max

t+N

,..,v

t+N−1

t+N|t

) +

N−1

k=1

t+k|t

∞

−1

k=0

t+k

∞

. . .

(6)

or equivalently in a ”closed loop” formulation:

min

kRu

∞

+ max

t+1|t

∞

+ min

t+1

{. . . + min

t+N

−1

t+N

−1

∞

+ max

t+N

−1

,...,v

t+N

t+N|t

N−1

k=N

t+k|t

∞

· · ·

3 ROBUST MPC AS A MULTI-

PARAMETRIC OPTIMIZATION

The robust model predictive control problem formu-

lated before is based on the on-line solving of the as-

sociated min-max optimization problem:

min

max

J(x

, k

)

subj. to F

+ G

6 h

+ H

(7)

with k



, .., u

t+N

−1



, k

= {v

, .., v

t+N−1

}

and a convex cost function J(x

, k

) based on a

sum of ∞-norm terms. F

, G

, h

, H

translate

in a compact form the set of constraints in (5). Both

the cost function and the set of constraints depend on

the current state vector x

which plays the role of a

parameter. This parameterization of the optimization

problem to be solved at each sampling time trans-

forms the on-line location of the minimum argument

in a computationally prohibitive task. The alternative

solution is to explicitly formulate off-line the optimal

solution k

∗

) in terms of a piecewise linear func-

tion and further evaluate this function on-line.

3.1 The inner optimization

The inﬂuence of the disturbances in the form (7) can

be examined by the reconsideration of the extremal

possible combination of vertices in V for each pre-

diction stage completing the sequence k

∈ V ⊂ R

⇒ k

∈ V

⊂ R

N×p

(8)

Remark: For the inner optimization, the set of con-

straints is constituted only by the inequalities deﬁning

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

the polyhedral domain as in (3) and the constraints

imposed by the system dynamics in (1). This fact

is transparent from the deﬁnition of the predictive

control law, which allows any combination of distur-

bances satisfying (3). If one of these combinations is

not allowed by the set of constraints in (7), it means

in fact that the MPC law is infeasible.

Taking into account the convexity of the objective

function and the previous remark, it can be concluded

that the optimum for the inner optimization in (7) is

on the border of the feasible domain, more precisely

on one of the vertices of V

as long as it is deﬁned

as a polytope. Thus (7) becomes:

min

max

J(x

, k

)

subj. to F

+ G

6 h

+ H

l ∈ L, k

∈ V

(9)

with L = {1, 2, . . . , N

} and N

the number of ver-

tices in V

This means that the inner optimization in (7) will

act only on the set of vertices in V

. Further this

may be written as:

min

,µ

subj. to F

+ G

6 h

+ H

J(x

, k

) 6 µ

l ∈ L, k

∈ V

(10)

3.2 The outer optimization problem

An impediment in ﬁnding the explicit solution for (7)

is the expression of the cost function, given as a col-

lection of ∞-norm terms. In order to avoid the in-

herent difﬁculty of handling it, an equivalent linear

program (LP) (Kerrigan, 2004) formulation must be

achieved based on the idea that each ∞-norm term

can be bounded. The optimization problem is equiva-

lent with the minimization of the sum of these bounds.

This is resumed by the following result where the cost

function is considered as a sum of ∞-norm terms lin-

ear in the vector of unknowns x and parameters p (to

identify them, one can observe that for a ﬁx sequence

= ct and noting x = k

and p = x

in (7), the

cost function is a sum of kS

x + P

p + s

∞

terms,

with S

, P

, s

deﬁned after case).

Proposition 1. The formulations (1) and (2) are

equivalent:

(1)

K(p) = min

J(x, p) = min

i=1

x + P

p + s

∞

subject to A

x 6 b

+ B

(2)

K(p) = min

ρ,

{

}

subject to

- 1σ

6 S

x + P

p + s

6 1σ

, 1 6 i 6 n

i=1

6 ρ

x 6 b

+ B

where σ

, ρ ∈ R and 1 is a vector with unit entries.

3.3 RMPC multi-parametric

optimization problem

With the previous two transformations, the optimiza-

tion (7) can be rewritten as:

∗ (x

) = min

ρ,k

{

}











- 1σ

6 S

+ P

+ W

+ s

6 1σ

1 6 i 6 n, 1 6 l 6 N







i=1







6 1ρ

+ G

6 h

+ H

1 6 l 6 N

(11)

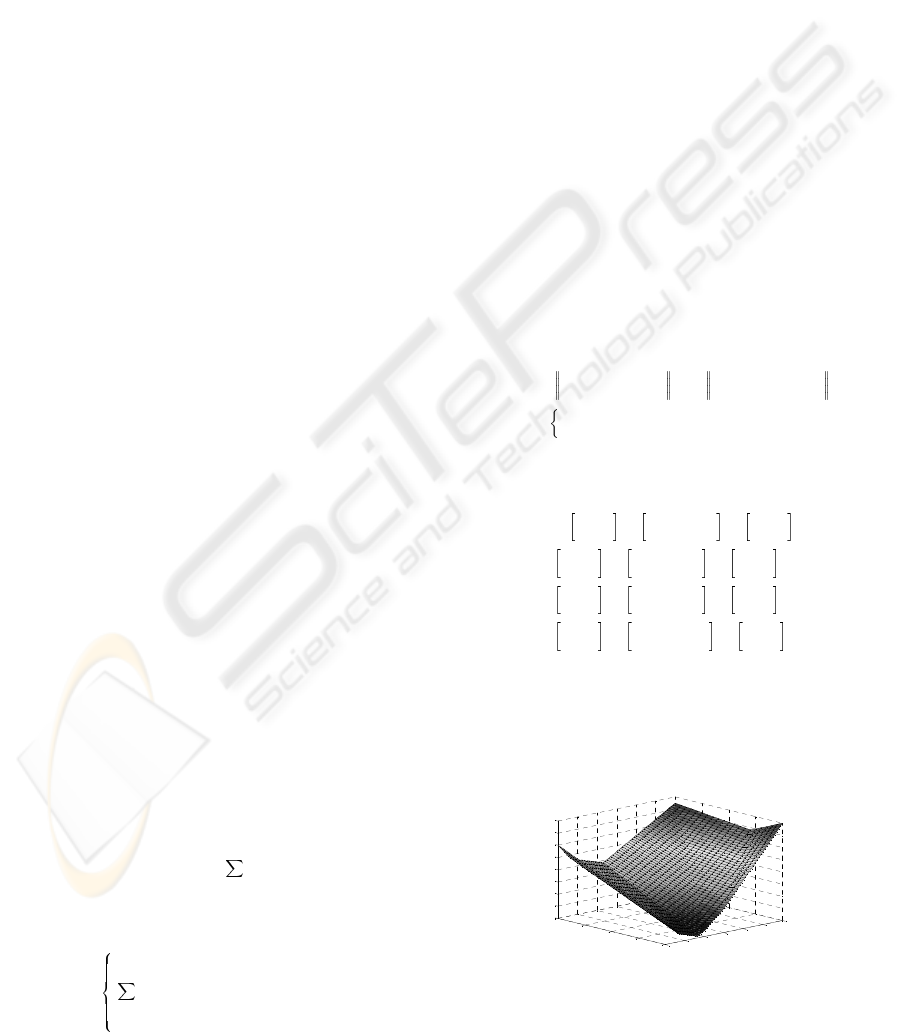
Example 1: To illustrate these transformations, con-

sider the parameter-free optimization (Fig. 1):

min

max

+ x

− 3

− x

+ 1

∞

− 2x

+ 1

+ 3x

− 7

∞

subject to

∈ [ - 1,1]

∈ [0, 6]

equivalent with:

min

,σ

,ρ

s.t. -

− 2

;

− 4

+ 2

;

− 1

− 4

;

+ 3

− 10

;

+ σ

6 ρ; σ

+ σ

6 ρ; x

∈ [0, 6]

which can be tackled by any LP solver with solution:

ρ]

∗

= [2.33 4.33 5.33 1.33 2.66 9.66]

-1

-0.5

0.5

Figure 1: Cost function for example 1.

A PARAMETERIZED POLYHEDRA APPROACH FOR THE EXPLICIT ROBUST MODEL PREDICTIVE CONTROL

4 THE EXPLICIT SOLUTION

In the following, the closed form of the RMPC law

is the main objective. It can be expressed as a func-

tion of parameters if a procedure of describing the

explicit solution of multi-parametric linear programs

(MPLP) is available. The literature on MPLP con-

tains the works of Gal and Nedoma (Gal and Nedoma,

1972) and further developments to linear, quadratic,

non-linear or mixed-integer solvers (Borelli, 2003).

Another procedure will be proposed here focusing on

the set of constraints and its geometrical represen-

tation. The feasible domain will be expressed as a

parametrized polyhedron. Due to the reformulation

of the optimization problem, the use of mixed vari-

ables is avoided. Thus the resulting algorithm dif-

fers from the solutions based on branch and bound

methods or other mixed integer linear solvers, being

mainly focused on the enumeration of the edges of an

augmented dimension polyhedron.

4.1 Parameterized polyhedra

A system of linear constraints deﬁne a polyhedron:

P = {x ∈ R

x = b

; A

x 6 b

} (12)

by dual Minkowski representation of generators

(Schrijver, 1986):

P = conv.hull {x

, . . . , x

} +

+cone {y

, . . . , y

} + lin.spaceZ

(13)

where conv.hullX denotes the set of convex combi-

nations of points in X, coneY denotes nonnegative

combinations of unidirectional rays and lin.spaceZ

represents a linear combination of bidirectional rays.

It can be rewritten as:

P =

(

x| x =

i=1

)

0 6 λ

6 1,

i=1

= 1 , γ

> 0 , ∀µ

(14)

Remark: The generators saturate all the equalities, the

lines saturate all the constraints and only the rays and

the vertices can verify but not saturate a part of the

inequalities.

The geometrical computations might be burdened

by the differences that have to be taken into consid-

eration between rays and lines. These problems are

overcome with an homogenous representation (Wilde,

1993):

D =













ξ x



∈ R

n+1





ξ x



= 0



ξ x



> 0











(15)

= [

−b

]



−b

0 · · · 0 1



(16)

The original polyhedron P is found intersecting D

with the hyper-plane of equation ξ = 1. Following

the same change of dimension, the rays, vertices and

lines have a similar uniﬁed homogenous description:

Y =



0 · · · 0 1 · · · 1



;

Z =



0 · · · 0



(17)

and the generators representation will be:

D =



ξ x







ξ x



Y λ

′

Z µ; λ

′

> 0



(18)

A parameterized polyhedron is deﬁned in the implicit

form by a ﬁnite number of inequalities and equali-

ties but the afﬁne part depends linearly on a parameter

vector p for both equalities and inequalities:

′

(p) =

x ∈ ℜ

x = B

p + b

; A

x 6 B

p + b

= x(p)| x(p) =

i=1

(p)x

(p) +

i=1

0 6 λ

(p) 6 1,

i=1

(p) = 1 , γ

> 0 , ∀µ

(19)

where z

are the lines, y

are the rays, x

are the ver-

tices and µ

, γ

, λ

the corresponding coefﬁcients.

Remark: Only the vertices are concerned by the pa-

rameterization of the polyhedron (parameterized ver-

tices x

(p)), the rays and the lines do not change with

the parameters’ variation.

The parameterized polyhedron P

′

(p) can be writ-

ten as a non-parameterized polyhedron in an aug-

mented space as:

′

(





∈ R

n+m



− B

= b

[ A

| − B

]

= b

)

(20)

with a homogenous representation given by:

D =

ξ x

ξ p

ξ x

ξ p

= 0

ξ x

ξ p

> 0

ξ x

ξ p

ξ x

ξ p

λ +

Y˜µ; ˜µ > 0

(21)

where

Z are as in (17), the matrices:

= [ A

| −B

| − b

] ;



−B

−b

0 · · · 0 0 · · · 0 1



and

λ, ˜µ are free-valued column vectors.

The form (19) faces an important difﬁculty as it

contains unknown parts, i.e. the parameterized ver-

tices x

(p).

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

The parameterized vertices corre-

spond to m-polyhedra in the augmented

(data(R

)+parameter(R

)) space as in (20);

consequently the original vertices are:

(p) = Proj



(

′

) ∩ S(p)



(22)

where Proj

(.) projects the combined space R

n+m

onto the original space R

and S(p) is the afﬁne sub-

space:

S(ˆp) =





∈ R

n+m



p = ˆp



(23)

and F

(

′

) is a m-face of

′

found as the inter-

section between

′

and the supporting hyperplanes

(Loechner and Wilde, 1997).

For each face of the polyhedron

′

, a set of ac-

tive constraints is well deﬁned, resulting in the fact

that each point



(p)



∈ F

(

′

) lies in a

subspace of dimension m and thus x and p are related

by:





x =



′



p +





(24)

where

′

are the subset of the inequal-

ities deﬁned previously, satisﬁed by saturation. If the

matrix





is not invertible, it corre-

sponds to faces F

(

′

)where for one given p more

than one point x ∈ R

is feasible and such combi-

nations do not match a vertex of P

′

(p). In fact this

case corresponds to the zones where P

′

(p) changes

its shape.

In the invertible case, the dependencies could be

rewritten:

(p) =





−1



′







−1





(25)

For the implementation of these theoretical results,

an enumeration of the m-faces must be available to-

gether with the k(> m) generators of each face

(

D) in a homogenous representation. If the pro-

jections:

P r

ξ x

(p)

ξ p



ξ x

(p)



; (26)

P r

ξ x

(p)

ξ p



ξ p



(27)

are deﬁned, then (22) could be rewritten as:



ξ x

(p)



= Pr

) Pr

)

−1





;

ξ x

(p)

ξ p

, j = 1..k

(28)

The case when the right inverse P r

)

−1

does not

exist results in the already mentioned conditions of an

m-face that does not deﬁne a unique vertex of P

′

(p).

Remark: Numerical methods (Leverge, 1994) exist

for implementing the double description of polyhedra.

The polyhedral duality allows both transformations,

from constraints to generators and conversely ((Lev-

erge, 1994), (Loechner and Wilde, 1997), (Motzkin

et al., 1953), (Schrijver, 1986), (Wilde, 1993) ).

4.2 Explicit solution of LP

Recalling the problem to be solved similar to (11):

∗

(p) = min

subject to A

x 6 B

p + b

(29)

with the optimal solution as a piecewise afﬁne func-

tion of the parameter.

Consider now a ﬁxed parameter p

. When ana-

lyzing the optimization problem (29) corresponding

to this value, a geometrical point of view can be used,

as in Chernikova algorithm (Leverge, 1994).

Proposition 2. For a linear problem three cases may

arise:

a) If the associated polyhedron P =

{x|A

x 6 B

+ b

} is empty, the problem is

infeasible;

b) If there exists a bidirectional ray z such that

z 6= 0 or there exists a unidirectional ray y such

that f

y 6 0, then the minimum is unbounded;

c) If all bidirectional rays z are such that

z = 0 and all unidirectional rays y are such

that f

y > 0, then the minimum is deﬁned by:

min



vertex of P



and the solution is:

S = conv.hull {x

′

, . . . , x

′

} +

+cone {y

′

, . . . , y

′

} + lin.spaceP

where x

′

are the vertices attaining the minimum and

′

are such that f

′

= 0.

Now extending this perspective to the multi-

parametric case for each p ∈ R

, a similar result

can be established.

Proposition 3. The solution of a multi-parametric

linear optimization problem is characterized by the

followings:

a) If there exists a bidirectional ray z such that

z 6= 0 or there exists a unidirectional ray y such

that f

y 6 0, then the minimum is unbounded;

b) For the sub domains of the parameter space

ifez

∈ R

with the associated polyhedron P =

{x|A

x 6 B

p + b

} empty while p ∈ D

ifez

the problem is infeasible (this can be restated in

terms of parameterized vertices: ”for the sub domains

where no parameterized vertex is available, the prob-

lem is infeasible”);

A PARAMETERIZED POLYHEDRA APPROACH FOR THE EXPLICIT ROBUST MODEL PREDICTIVE CONTROL

c) If all bidirectional rays z are such that f

z = 0

and all unidirectional rays y are such that f

y > 0,

then the sub domains D

can be deﬁned such that the

minimum:

min



(p)|x

(p) vertex of P (p)



is attained by the same subset of vertices of . The

complete solution for this sub domain is:

(p) = conv.hull {x

′

(p), . . . , x

′

(p)} +

+cone {y

′

, . . . , y

′

} + lin.spaceP (p)

where x

′

are the vertices corresponding to the mini-

mum and y

′

are such that f

′

= 0.

One has to observe that our goal is to ﬁnd the ex-

plicit solution for the LP derived from the optimiza-

tion problem in robust MPC which has some particu-

larities:

• The linearity space is empty since the cost function

is positive convex.

• There is no unidirectional ray such that because this

will imply that the cost function is not convex.

• A single value in S

(p) is to be used on-line in

MPC.

Proposition 4. The solution of a multi-parametric

linear optimization problem within robust MPC satis-

ﬁes:

a) The problem is infeasible for the sub domains

ifez

∈ R

where no parameterized vertex is avail-

able;

b) Sub domains D

are deﬁned as the

zones for which the solution S

(p) =

conv.hull {x

′

, . . . , x

′

} is given by the same

set of parameterized vertices satisfying:

′

= . . . = f

′

= min



(p)|x

(p) vertex of P (p)



Remark: As the parameters in (29) vary inside the

parameter space, the vertices of the optimization do-

main may split, shift or merge. The global optimum

will follow this evolution within the parameter space

as the optimum is a continuous function of parameter.

From a practical point of view the implementation

of this result is direct and follows the steps:

1. Find the expression of the parameterized feasible

domain in the augmented data+parameter space:

x 6 B

p+b

⇔ [

|−B

]





6 b

2. Find the m-vertices where n is the dimension of the

parameter space.

3. Retain only those corresponding to parameterized

vertices by ignoring those with non-invertible pro-

jection on the parameter space

4. Compute validity domain D

for each parameter-

ized vertex

5. Compare each pair of vertices. In the case of a non-

empty intersection of their validity domains, split

them using the linear cost function. The ﬁnal ex-

pression will be a union of regions corresponding

to the parameterized vertices containing the opti-

mum.

A special attention must be given to the step 5 with

the iterative comparison of the vertices and their va-

lidity domains. A possible routine may be based on

the following procedure.

procedure CutDomains (VD: the set of

all validity domains)

n=cardinal (VD)

i=1; j=2

while i<n+1

while j<n+1

if V D

∩ V D

6= ∅

if f

6 f

then V D

= V D

− V D

if f

6 f

then V D

= V D

− V D

j=j+1

endif

end

i=i+1

end

Remark: The procedure is initialized with the set

of validity domains obtained after the edges’ enumer-

ation (step 2).

Remark: The difference of two convex domains is

not a close operation and thus the output of the proce-

dure is a union of convex sub domains of the parame-

ters space which do not necessarily cover the entire

(step 4).

From the RMPC point of view, the difference:

ℵ = R

\ {∪D

; k = 1..n

} (30)

describes the regions of infeasible parameters.

Once the set of parameter space sub domains D

created, it can be used in an on-line optimization ﬁnd-

ing the control sequence for robust MPC.

Algorithm 2 (on-line solver)

1. Find the appurtenance set D

; k = 1..n

for the

current parameter p. Return infeasible if no D

found.

2. Compute k

MP C

= x

(p) using the piecewise for-

mulation of the parameterized vertices as in (25)

and effectively apply the ﬁrst component.

3. Restart from 1 with the new p.

5 EXAMPLE

Consider the model (Scokaert and Mayne, 1998):

t+1

= x

+ u

+ v

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

In order to illustrate the ideas of RMPC presented ear-

lier, a two step prediction is considered and thus the

following optimization problem is to be solved at each

sampling time:

V (x

) = min

t+1

k=0



t+k|t



+ 10 |u

t+k

s.t.











- 1.2 6 x

t+k|t

6 2, k = 0, 1, 2

- 1 6 x

t+2|t

6 1,

- 1 6 v

t+k

6 1, k = 0, 1

(31)

Ignoring the disturbances, the explicit solution of the

problem can be found using the geometrical approach

presented in the previous section by inspecting the 22

parameterized vertices. After the stage of discrimina-

tion of the validity domains, the explicit RMPC law is

found as:

Afﬁne control law Validity domain

= −x

− 1 −1.2 6 x

6 −1

0 −1 6 x

6 0

0 0 6 x

6 1

= −x

+ 1 1 6 x

6 2

It can be observed that there are two domains with

the same control law due to the fact that the cost

function changes its slope and thus the maximum lies

on different parameterized vertices in the augmented

space. In this case, as their union is a convex set, they

can be collated in a single set. In the general case, this

operation can be done using tools of convex recog-

nition of union of polyhedra (see (Bemporad et al.,

2002a) for details).

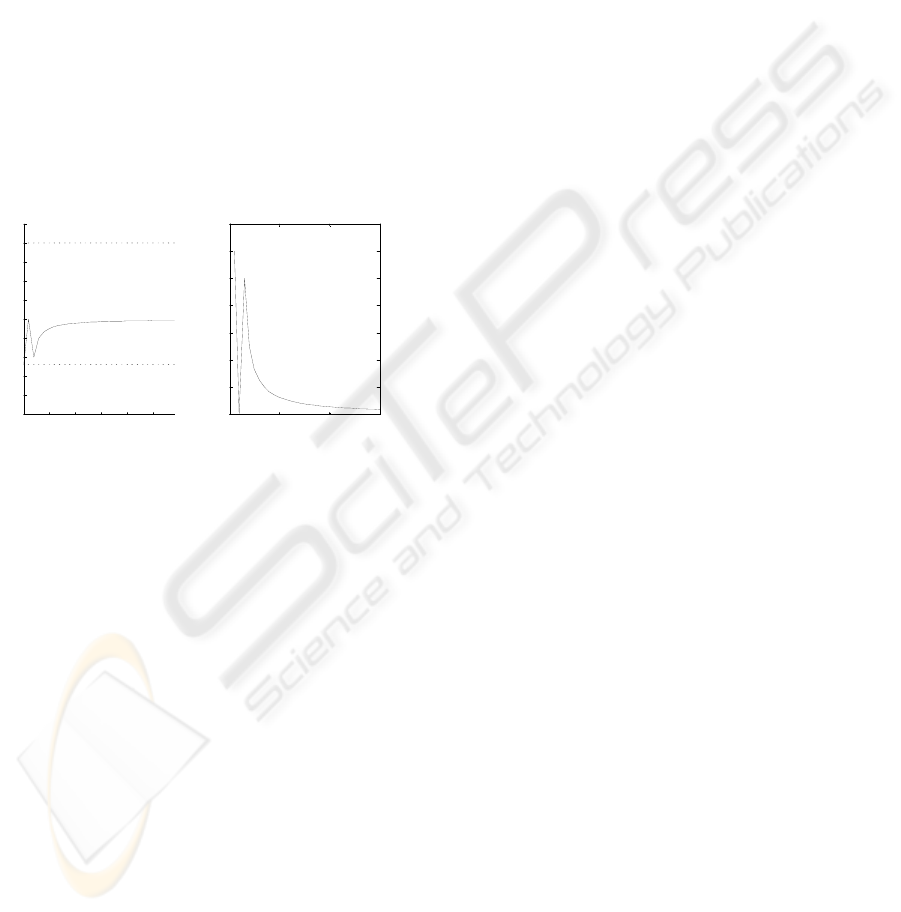
Simulating this control law for an initial condition

= −1.2 proves to keep the system trajectory in-

side the constraints in the disturbance free case (Fig-

ure 2a). If the same controller is used with v

−1/k, k > 1 , the trajectory will violate the con-

straints (Figure 2b).

Further if the robust MPC explicit formulation is to

be achieved then the min-max version of (31) is to be

solved:

V (x

) = min

t+1

max

t+1

k=0



t+k|t



+ 10 |u

t+k

s.t.











- 1.2 6 x

t+k|t

6 2, k = 0, 1, 2

- 1 6 x

t+2|t

6 1,

- 1 6 v

t+k

6 1, k = 0, 1

(32)

In this form, there is no solution as the optimization

is infeasible. In fact there is no control law at ﬁrst

sampling time:

t|t

= a

+ b

t+1|t

= a

+ b

t|t

+ c

which can keep robustly the system trajectory within

the constraints. This fact is obvious as long as an

0 5 10 15 20 25

-2

-1

b) Nominal MPC with disturbance

0 10 20 30

0.2

0.4

0.6

0.8

b) Command - u - MPC w.d.

0 5 10 15 20 25

-2

-1

a) Nominal MPC - disturbance free

0 10 20 30

0.05

0.1

0.15

0.2

a) Command - u - MPC d.f.

Figure 2: a) Left: Nominal MPC - disturbance-free case;

b) Right: Nominal MPC for the system affected by distur-

bances.

”open-loop” type of RMPC is considered, where the

cumulative damage of the disturbances can not be

mitigated. When writing explicitly the end-point con-

straints in (32) for the extremal combinations of dis-

turbances, this becomes evident as:



t+1







⇒

−1 6 x

+ u

t|t

+ u

t+1|t

+ 2 6 1 ⇒

−3 6 x

+ u

t|t

+ u

t+1|t

6 −1;



t+1





−1



⇒

−1 6 x

+ u

t|t

+ u

t+1|t

− 2 6 1 ⇒

1 6 x

+ u

t|t

+ u

t+1|t

6 3

which means that there is no control combination to

maintain the law feasible without a prior knowledge

of disturbances. However the so called ”closed loop”

formulation provides the necessary degrees of free-

dom in this sense. One has to solve:

V (x

) = min

max

min

t+1

max

t+1

k=0



t+k|t



+ 10 |u

t+k

s.t.











- 1.2 6 x

t+k|t

6 2, k = 0, 1, 2

- 1 6 x

t+2|t

6 1,

- 1 6 v

t+k

6 1, k = 0, 1

(33)

Following the theoretical result in section 4, the ex-

plicit solution can be achieved by solving the inner

minimization:

V (x

, u

, v

) = min

t+1

max

t+1

| +

+ |x

+ u

+ ν

| + 10 |u

t+1

s.t.











- 1.2 6 x

t+k|t

6 2, k = 0, 1, 2

- 1 6 x

t+2|t

6 1,

- 1 6 v

t+k

6 1, k = 0, 1

(34)

A PARAMETERIZED POLYHEDRA APPROACH FOR THE EXPLICIT ROBUST MODEL PREDICTIVE CONTROL

The solution using the geometrical approach is imme-

diate as there are exactly 2 parameterized vertices on

which the minimum lies and associated control law is:

t+1|t

= −(x

t|t

+ν

) = −x

t+1

for - 1.2 6 x

6 2

Notice that the control law uses the additional infor-

mation available in comparison with (32). With this

result, for the outer optimization problem:

min

max

| +



11x

t+1|t



+ |10u

s.t.



- 1.2 6 x

t+k|t

6 2, k = 0, 1

- 1 6 v

6 1

(35)

the explicit solution is once more immediate as there

are only two non-degenerate parameterized vertices

describing the geometric locus of the minimum. Ap-

plying this RMPC law:

= −x

for - 1.2 6 x

6 2

the system affected by disturbances is regulated to the

origin (Figure 3). The solutions of the optimization

0 5 10 15 20 25

-2.5

-2

-1.5

-1

-0.5

0.5

1.5

2.5

Robust MPC

0 10 20 30

0.2

0.4

0.6

0.8

1.2

1.4

Command - u

Figure 3: System trajectory with robust MPC law.

problems in (31), (34), (35) were obtained using pa-

rameterized polyhedra routines in 2, 0.39 and 0.91

seconds respectively. However for complex system

the computational time may explode as the number

of parameterized vertices has an exponential depen-

dence on the number of constraints added during the

transformation stages.

6 CONCLUSION

The paper used a uniﬁed approach for the con-

straints handling in the context of RMPC conﬁrming

the formulation of the optimal sequence as a multi-

parametric quadratic problem. The explicit solution

of this problem was synthesized by means of para-

meterized polyhedra. This geometrical approach pro-

poses an alternative to the recent methods presented

in the literature. Its advantages might be the fact that

optimum lies on the parameterized vertices providing

a natural constant linear afﬁne dependence in the con-

text parameters. An aspect which may receive further

attention is the enumeration of faces for the parame-

terized polyhedra which may turn to be a computa-

tionally demanding task.

REFERENCES

Bemporad, A., Borelli, F., and Morari, M. (2001). Robust

model predictive control: Piecewise linear explicit so-

lution. In Proc. European Control Conference.

Bemporad, A., Fukuda, K., and Torrisi, F. (2002a). Convex-

ity recognition of the union of polyhedra. In Compu-

tational Geometry, Vol. 18.

Bemporad, A., Morari, M., Dua, V., and Pistikopoulos, E.

(2002b). The explicit linear quadratic regulator for

constrained systems. In Automatica, vol. 38.

Borelli, F. (2003). Constrained Optimal Control of Linear

and Hybrid Systems. Springer-Verlag, Berlin.

Gal, T. and Nedoma, J. (1972). Multiparametric linear pro-

gramming. In Management Science, 18.

Goodwin, G., Seron, M., and Dona, J. D. (2004). Con-

strained Control and Estimation. Springer-Verlag,

Berlin.

Kerrigan, E. (2000). Robust Constraint Satisfaction: Invari-

ant Sets and Predictive Control. PhD Thesis, Univer-

sity of Cambridge.

Kerrigan, E. (2004). Feedback min-max model predictive

control using a single linear program: Robust stability

and the explicit solution. In International Journal of

Robust and Nonlinear Control, vol.14.

Kothare, M., Balakrishnan, V., and Morari, M. (1996). Ro-

bust constrained model predictive control using linear

matrix inequalities. In Automatica, vol. 32.

Leverge, H. (1994). A note on chernikova’s algorithm. In

Technical Report 635. IRISA, France.

Loechner, V. and Wilde, D. (1997). Parameterized poly-

hedra and their vertices. In Int. Journal of Parallel

Programming, vol. 25.

Maciejowski, J. (2002). Predictive Control with Con-

straints. Prentice Hall, UK.

Motzkin, T., Raiffa, H., Thompson, G., and Thrall, R.

(1953). The double description method. In Theodore

S. Motzkin: Selected Papers. Birkhauser, Boston.

Olaru, S. and Dumur, D. (2004). A parameterized polyhedra

approach for explicit constrained predictivecontrol. In

43rd IEEE Conference on Decision and Control.

Rossiter, J. (2003). Model-based Predictive Control. A

practical approach. CRC Press.

Schrijver, A. (1986). Theory of Linear and Integer Pro-

gramming. John Wiley and Sons, NY.

Scokaert, P. and Mayne, D. (1998). Min-max feedback

model predictive control for constrained linear sys-

tems. In IEEE Trans. Automatic Control, 43.

Seron, M., Goodwin, G., and Dona, J. D. (2002). Charac-

terisation of receding horizon control for constrained

linear systems. In Asian Journal of Control, vol. 5.

Wilde, D. (1993). A library for doing polyhedral operations.

In Technical report 785. IRISA, France.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL