
STABLE REPETITIVE CONTROL BY FREQUENCY ALIASING
James D. Ratcliffe, Paul L. Lewin and Eric Rogers
University of Southampton
School of Electronics and Computer Science, University Road, Southampton, SO17 1BJ, United Kingdom
Jari J. Hätönen, Thomas J. Harte and David H. Owens
University of Sheffield
Department of Automatic Control and Systems Engineering, Mappin Street, Sheffield, S1 3JD, United Kingdom
Keywords:
Repetitive control, signal processing.
Abstract:
A filtering technique based on frequency aliasing which was initially developed for Iterative Learning Control
is modified so that it can be implemented in real-time and is suitable for Repetitive Control. The aliasing
technique is experimentally verified on a gantry robot facility, which manipulates payloads from a dispenser
onto a constant velocity conveyor. A parallel arrangement consisting of a three-term feedback controller
and a simple structure repetitive controller is used to control the robot. Without the aliasing technique, the
combined control system becomes unstable very rapidly. In contrast, when the aliasing technique is applied,
1000 repetitions are successfully completed and no indications of impending instability can be seen.
1 INTRODUCTION
Repetitive Control (RC) is concerned with improv-
ing the performance of trajectory tracking and set-
point control problems in the cases where the refer-
ence trajectory is repeated ad infinitum or the distur-
bances are repeated and occur in a regularly timed
manner. Examples of this type of application include
food production facilities, printing presses and bulk
product transfer systems such as conveyors. Appli-
cations such as these, tend to be controlled by stan-
dard feedback techniques such as the three-term or
PID controller. This is because they are cheap, ro-
bust methods which are relatively simple to install and
tune, and the production facility can be made opera-
tional rapidly.
The disadvantage of using a simple structure feed-
back controller is that for a repetitive process, the
same level of error will be obtained for each rep-
etition. It is also likely that as the plant dynam-
ics change, due to wear for example, the feedback
controller will gradually become de-tuned and con-
trol performance will reduce, necessitating regular re-
tuning to counteract this.
Repetitive control utilises the error data from pre-
vious executions of the task, to modify the input pro-
file, which is supplied to the plant at the next trial, in
a way which seeks to reduce the tracking error. Theo-
retically, this technique will converge asymptotically
to zero tracking error, if non-repeating disturbances
are not present. This is a property which should make
RC very attractive to industrial applications. How-
ever, RC also has some disadvantages particularly
concerned with algorithm stability. Generally, an al-
gorithm is found to reduce the tracking error for a
number of iterations, but then gradually becomes un-
stable and the tracking error increases exponentially.
Evidently, this type of behaviour is unacceptable in an
industrial context.
It has generally been recognised that this unsta-
ble behaviour is caused by certain signals, which can
build up within the cyclic learning loop. In particu-
lar, these signals include high frequency noise, or low
frequency signals which have an input/output phase
shift larger than 180
◦
. Simple structure learning tech-
niques are unable to compensate for these signals
(Chen and Longman, 2002). Therefore at each rep-
etition, more are added to the learnt signal until this
becomes corrupted to the point where the plant can-
not operate. Standard practice to prevent instability
from occurring is to filter these signals from the error
data. Unfortunately, conventional filtering techniques
induce additional phase lag into the control system,
which results in reduced controller performance and
non-zero residual tracking error. It is therefore nec-
essary to filter the data without introducing additional
phase shift, by using zero-phase methods.
This paper investigates the development of stable,
323
D. Ratcliffe J., L. Lewin P., Rogers E., J. Hätönen J., J. Harte T. and H. Owens D. (2005).
STABLE REPETITIVE CONTROL BY FREQUENCY ALIASING.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 323-326
Copyright
c
SciTePress

simple structure, repetitive control techniques by us-
ing a frequency aliasing method, as a means of filter-
ing unwanted information from the learning loop and
hence maintaining stability, in an inherently unstable
control system. The aliasing technique was originally
developed by the authors in the ILC context (Ratcliffe
et al., 2005a), but can be ported to the RC context, to
provide a simple, real-time zero-phase filtering tech-
nique. In contrast, many stabilisation techniques in
RC rely upon the use of batch zero-phase filtering,
which is not easily implemented in real-time, as it is
inherently a non-causal technique. Achieving batch
zero-phase filtering in RC systems, involves operat-
ing the plant and simultaneously batch filtering data
over a period of several repetitions, see for example
(Chen and Longman, 1999; Songchon and Longman,
2001).
2 REAL-TIME ALIASING
Shannon’s sampling theorem states that to record a
signal of a given frequency in a discrete-time sys-
tem, the sample frequency must be at least twice the
frequency of the signal. If this requirement is not
met, then frequency aliasing occurs and the higher
frequency components of the original signal are lost.
In most applications, aliasing is a drawback, usu-
ally redressed by means of anti-aliasing filters. In this
application, aliasing is beneficially used to remove the
effects of the undesired frequencies from the learning
controller. The controller configuration uses a simple
structure P-type repetitive controller in parallel with
a PID feedback controller. The feedback controller is
required to smooth the output produced by the alias-
ing technique, but is also useful for producing good
tracking performance during the first few repetitions.
The feedback controller also provides additional ro-
bustness to non-repeating disturbances and can re-
spond to sudden disturbances much more rapidly than
the learning controller. In addition to the feedback
and feed-forward controllers, an additional aliasing
module is implemented on the output generated by
the learning controller. The aliasing module samples
the output generated by the learning controller at a
frequency less than twice the lowest frequency which
needs to be removed from the learning process. In this
way, undesired frequencies are aliased to a lower fre-
quency, while the aliasing filter still allows the RC to
learn frequencies below the alias cut-off. As long as
the cut off frequency is greater than the frequencies
which need to be learnt to satisfy the reference de-
mand, the loss of data caused by aliasing does not pre-
vent the learning controller from improving the per-
formance of the overall system.
In the following analysis, ‘alias frequency’ is used
to describe the sample frequency of the aliasing fil-
ter. ‘Feedback frequency’ is used to describe the sam-
ple frequency of the remaining control system(1kHz).
‘Alias gap’ (ag) is used to relate the alias frequency to
the feedback frequency. The alias gap is the number
of feedback frequency sample instants between each
alias frequency sample instant.
Using a zero-order-hold approach for the aliasing
module is not suitable, as the aliasing filter gener-
ates a signal, which relates poorly to the original non-
aliased signal, due to large step changes in the con-
trol voltage. In a non-causal approach which can
be used for ILC, instead of holding the signal value
constant between aliasing samples, it is possible to
calculate the gradient between adjacent samples and
join them by linear interpolation, a technique which
is commonly used in practical signal processing. Fol-
lowing the successful completion of an iteration, the
ILC algorithm computes the next ILC component of
the plant input vector at feedback frequency. This in-
put vector is likely to contain unwanted frequencies.
The aliasing module then re-samples the input vec-
tor at the aliasing frequency, removing all frequencies
above the aliasing cut-off. The input vector now con-
sists of far fewer sample instants than are required for
real-time operation. Linear interpolation is used to
connect the aliasing frequency sample instants, so that
a smooth signal is produced when the interpolated
signal is re-sampled at feedback frequency. During
the next iteration, each sample instant of the aliased
ILC vector is summed with the input produced by the
feedback controller.
The same principle can be implemented in repeti-
tive control in a causal manner, by delaying the learn-
ing update by a number of samples equal to the alias
gap. The linear interpolation method can then be per-
formed one sample at a time, rather than in a batch.
The flowchart in Figure 1 describes the sequence of
events.
3 TEST FACILITY
The experimental results presented in Sections 4 and
5 were obtained by implementing the parallel config-
uration controller on the test facility depicted in Fig-
ure 2. It consists of a 3-axis gantry robot mounted
above one end of a plastic chain conveyor. The robot
is required to collect payloads from an asynchronous
dispenser, then transfer them to the conveyor which
is travelling at constant velocity. Once the payloads
reach the opposite end of the conveyor, they are fed
into a return mechanism which cycles the payloads
back to the dispenser. This allows many repetitions
to be performed, with a minimal number of payloads.
The robot and conveyor emulate many synchronous

Iscurrentsample
amultipleof ag?
ComputeandoutputthePIDandRC setpoints
forthecurrentsample,storeintemporarymemory
Addvalueof‘increment’
to‘storedvalue’
SaveinRCmemorylocation
‘currentsample’ - ag
SavetheRCcomponentdirectlyto
RCmemoryat‘currentsample’ location
ComputedifferencebetweenRCmemoryat
‘currentsample’ and‘currentsample’ - ag
Dividedifferenceby ag
toobtain‘increment’
Set‘storedvalue’ totheRCmemory
valueat‘currentsample’ - ag
YesNo
Figure 1: Program operation flowchart (ag = alias gap)
placement operations which can be found in indus-
try. A detailed description of the robot and models
for each axis can be found in (Ratcliffe et al., 2005b).
Figure 2: Gantry robot, conveyor and payload dispenser
4 INITIAL IMPLEMENTATION
Before implementing the aliasing technique, the plant
is operated without any form of filtering. The feed-
back controller and the learning controller both oper-
ate with a sample frequency of 1kHz. Figure 3 dis-
plays the mse results for each axis on a logarithmic
vertical scale. The learning gain β was set to 10 and
100. The values of mse for iteration 1 represent the
tracking performance, which is achieved by the feed-
back controller alone, because at this stage the repet-
itive controller has had no opportunity to learn any-
thing from previous trials. Clearly, the simple struc-
ture repetitive controller can significantly improve the
tracking performance, as the mse for each axis is
reduced by approximately two orders of magnitude.
0 20 40 60 80 100 120 140
10
−2
10
−1
10
0
10
1
x−axis mse
mse (mm
2
)
0 20 40 60 80 100 120 140
10
−1
10
0
10
1
10
2
y−axis mse
mse (mm
2
)
0 20 40 60 80 100 120 140
10
−2
10
−1
10
0
z−axis mse
Iteration
mse (mm
2
)
gain = 100
gain = 10
Figure 3: mse for 1000 repetitions with alias gap = 70
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−0.4
−0.2
0
0.2
0.4
Input (V)
X−axis, PID component
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−2
−1
0
1
2
Input (V)
RC component
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−1
−0.5
0
0.5
Error (mm)
Time (s)
Figure 4: X-axis inputs and tracking error (repetition 20)
Higher learning gain also results in faster convergence
to minimum error as expected. However, with β equal
to 100, the X-axis mse begins to increase after 17 iter-
ations, which is a clear indication of instability. This
is less noticeable for β equal to 10, but for both val-
ues of gain, the robot visibly began to shake as the
algorithm became unstable.
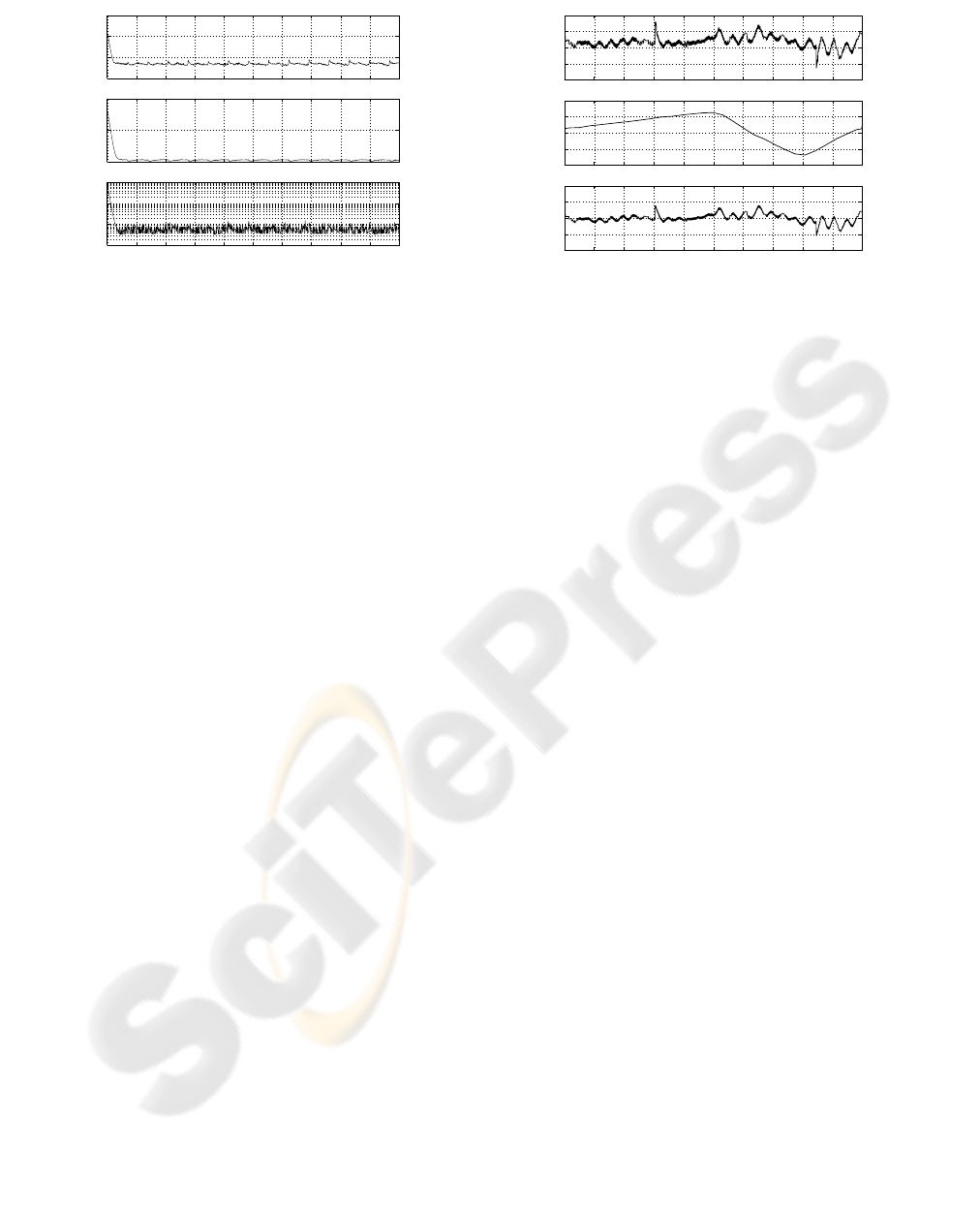
Figure 4 shows the X-axis feedback controller in-
put, repetitive controller input and measured track-
ing error for iteration 20 with β equal to 100. All
three signals are heavily corrupted by a sinusoid of
frequency 13-14 Hz (81-87 rad/s). Referring to fre-
quency response plots for the robot axes, this fre-
quency corresponds well to a pair of complex con-
jugate poles in the dynamic response of the X-axis.
Effectively, a resonant frequency is allowed to build
up within the learning loop.
5 WITH ALIASING
To restore stability, it is necessary to prevent this reso-
nant frequency from building up in the learning loop.
With the system operating at a sample frequency of 1
0 100 200 300 400 500 600 700 800 900 1000
10
−4
10
−2
10
0
10
2
mse (mm
2
)
x−axis mse
0 100 200 300 400 500 600 700 800 900 1000
10
−2
10
0
10
2
mse (mm
2
)
y−axis mse
0 100 200 300 400 500 600 700 800 900 1000
10
−3
10
−2
10
−1
10
0
mse (mm
2
)
z−axis mse
Figure 5: mse for 1000 repetitions (alias gap = 70, β = 100)
kHz, an alias gap of 70 produces an aliasing frequency
of 14.28 Hz. Shannon’s sampling theorem then stip-
ulates that only signals of half this frequency can be
recorded. Therefore, the aliasing module removes all
signals of frequency larger that 7.14 Hz, including the
resonant frequency between 13 and 14 Hz. Figure 5
displays the mse results for 1000 repetitions, when the
aliasing module is implemented with a alias gap of 70
and the learning gain is equal to 100. The mse is re-
duced by over two orders of magnitude for each axis
and although it oscillates about a mean value, there
is no indication that it increases. The 1000 repetition
test does not guarantee that the control system will be
stable for an infinite number of repetitions. However,
compared to the original controller without aliasing
which achieved 20 repetitions, there is a significant
improvement.
Figure 6 shows the X-axis controller inputs and
recorded tracking error for iteration 1000 with the
alias gap equal to 70. Although the tracking error still
contains sinusoidal oscillations in the frequency range
13-14 Hz, these are clearly being stimulated by the
feedback controller and not the learning controller.
As the feedback controller has no learning or mem-
ory capabilities, the resonant frequency cannot grow
at each repetition.
Referring back to Figure 5, the underlying cause
behind the cyclic variation in mse is not yet under-
stood and requires further investigation. One possible
reason which can be suggested immediately is that the
variation is related to the alias gap number. To investi-
gate this hypothesis, the 1000 repetition test was per-
formed with an alias gap of 100. The increase in alias
gap value has a direct influence on the error reduction,
because the frequency range which can pass through
the aliasing module has been reduced. Therefore the
error reduction is now less than two orders of magni-
tude. However, the amplitude of the cyclic variation
in mse has been greatly reduced and the cycles now
occur every 50 repetitions. Evidently there is a link
between the alias gap and the variation which requires
further investigation.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−0.5
−0.4
−0.3
−0.2
−0.1
Input (V)
X−axis, PID component
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−2
−1
0
1
2
Input (V)
RC component
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−0.4
−0.2
0
0.2
0.4
Error (mm)
Time (s)
Figure 6: X-axis inputs and tracking error (repetition 1000,
ag = 70, β = 100)
6 CONCLUSIONS
The aliasing technique which was initially developed
for iterative learning control has been successfully
converted to a simple, causal operation which can be
calculated at each sampling instant in a repetitive con-
trol context. Experimental validation demonstrates
that the stability of a simple structure repetitive con-
troller can be greatly improved by using the aliasing
technique.
REFERENCES
Chen, H.-J. and Longman, R. (1999). The importance
of smooth updates in producing good error levels in
repetitive control. In Proceedings of the 38th IEEE
Conference on Decision and Control, Phoenix, Ari-
zona, pages 258–263.
Chen, K. and Longman, R. (2002). Stability issues using fir
filtering in repetitive control. Advances in the Astro-
nautical Sciences, 112(2):1321–1340.
Ratcliffe, J., Hätönen, J., Lewin, P., Rogers, E., Harte, T.,
and Owens, D. (2005a). P-type iterative learning con-
trol for systems that contain resonance. Accepted by
International Journal of Adaptive Control and Signal
Processing.
Ratcliffe, J., van Duinkerken, L., Lewin, P., Rogers, E.,
Hätönen, J., Harte, T., and Owens, D. (2005b). Fast
norm-optimal iterative learning control for industrial
applications. In Proceedings of the 24th American
Control Conference, Portland, pages 1951-1956.
Songchon, T. and Longman, R. (2001). On the waterbed
effect in repetitive control using zero-phase filtering.
Advances in the Astronautical Sciences, 108:1321–
1340.
