FREEZING ALARM SYSTEM BASED ON TIME SERIES

ANALISYS

Carmen Morató,.M.T.Castellanos, A.M.Tarquis, Enriqueta G. Mouton

Departamento de Matemática Aplicada, E.T.S.I.Agrónomos, Universidad Politécnica de Madrid

Keywords: Time series, ARIMA, freezing control, risk index, prevention.

Abstract: The aim of this work is to design an alarm system that allows protecting and preventing crop-freezing damages

taking decisions with enough time to react. A first step was to obtain a temperature forecast mode. In this line an

hourly temperature series was analyzed with Box-Jenkins methodology ( ARIMA models). An alarm system is

designed based on these forecast, at each 12 hours, in the air temperatures obtained each hour at real time and in

the average errors between real and forecast each hour and each 12 hours. This system generates an index alarm

that is related with the risk intensity that over a certain value will activate several sensors. This system is

applicable to any area adjusting conveniently the parameters and the ARIMA model.

1 INTRODUCTION

Temperatures are one of the most important variable in

the climatic influence, for this reason its forecast add a

privilege information in agriculture to select the crops

and to avoid crop damages, specially low temperatures

and freezing. Studies done by Cao and Moss (1989),

Jamieson et al. (1995) and Landau et al. (2000), point

out the relevance of temperature in crops growth

through regression functions. Several temperature

models have been developed in order to simulate it

through the daily maximums and minimums of one

specific region (Jamieson et al, 1995), or with less

accuracy such as monthly temperatures (Castellanos,

1997) or annual oscillations (Fernández, 1992).

The design of an alarm system based in forecast and

real temperatures permit to reduce the freezing risk

knowing that there is a high probability that this event

will occur in the short future. These alarms varies with

a crop threshold temperature (Ta) and a security

margin (Tu) that protect and give enough time to have

a positive sensors action avoiding freezing crop

damage or a reduction in final crop production. This

system could be used for greenhouse crops as well as

for tree fruit and extensive crops.

Air temperature is a temporal serie that can be

modeled using different techniques, one of them

autoregressive (AR) integrated (I) moving averaging

(MA) (Box and Jenkins, 1970; McMichael and

Hunter, 1972; Kantz and Schreiber, 1997;

Montgomery and Zarnowitz, 1998). The aim of this

modeling approach is to express the current time series

values as a linear function of past time series values

(the autoregressive component) and current and lagged

values of a white noise process (moving average

component) it means to separate the observed

elements into two components: the first is related to

the organized part (including tendency, seasonality and

cycles) and the second is the random residuals or white

noise.

This work pretends to use a stochastic model to

forecast hourly temperature to be included in an alarm

system based on ARIMA technique. The alarm system

design is in function of a freezing risk index (RI) for a

certain crop. This RI is evaluated through forecasted

temperature (Tf) and means error (ME).

2 MATERIAL AND METHODS

Hourly temperature series have been obtained from

meteorological station at Comunidad de Madrid

(Spain) located at 40ª 26’ 36’’ N; 3ª 44’ 18’’ W and an

altitude of 595 m.

To modeling this time series Box-Jenkins algorithm

and methodology have been used (Box and Jenkins,

1970). This ARIMA models have in account the

probabilistic behavior of the studied variable to

forecast the future values in a confidence interval.

360

Morató C., T.Castellanos M., M. Tarquis A. and G. Mouton E. (2005).

FREEZING ALARM SYSTEM BASED ON TIME SERIES ANALISYS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 360-363

DOI: 10.5220/0001179403600363

 SciTePress

Mathematically speaking a time series are discrete

observations over the dynamic stage of a variable, in

this case is hourly temperature (W

). It’s structure

could be described as a non stationary process. Box-

Jenkins methodology should be applied on stationary

series, consequently several transformations should be

done to obtain new variables (Z

) that obey to the same

probability density function and a variance with

independent from time. The first step to be done is to

get a stationary series. Commonly this is obtained

differentiated the original series

W seasonally,

24−

−=

ttt

WWZ . Once that an stationary series is

obtained, three steps are essential in this methodology

(Bowerman y O'Connell, 1987):

-Identification of possible models: based on the

behavior the simple autocorrelation function and

partial autocorrelation function, the parameters that

express the influence of the preceding values or white

noises in each one are calculated. (Matalas, 1967).

-Estimation of the parameters’model: the models

obtained in the previous step are adjusted to the series

through parameters estimation (Carlson 1970).

-Contrast of forecast versus data: a residual analysis

for each model is done to choose the best one. This

model is going to be used to forecast the values

(Noakes, 1985). If the series was differentiated to

obtain stationary, then the inverse process should be

done with the forecast values.

Temperature time series used in this work are hourly

and the seasonal period is 24. However, it has been

checked that different forecast intervals give better

results. A forecast interval of 12 hours has been

applied (Castellanos et al., 2005).

Hourly temperature forecast has been made during

the coldest months (november to april) at the

meteorological station location and the hourly error

and mean error (ME) have been calculated to obtain a

minimum threshold value (E = -1.5).

= Tr – Tf

ME =

∑

where Tr is the real temperature; Tf the estimated

temperature and T the number of forecasted

temperatures.

It has studied the cases where the temperatures are

closed or under zero and the real temperature is lower

than the forecast one. These are the cases where the

risk of freezing hours begin to increase and at this

situation the alarm system has its meaning.

A decision algorithm is designed to detect the

freezing risk hours and then to turn on the alarm with a

risk index depending on the probability of the event.

The risk index will varies through time mean while the

real temperature is know each hour. The initial

parameters established are: the alarm temperature (Ta),

the security threshold (Tu) and the ME threshold. Ta is

specific of each crop and directly related to the base

temperature. Tu is added to Ta depending on

topographic characteristics, crop market value and, in

general, the risk assumed for crops’ protection.

The mechanism is as follow:

Initialization of the paramenters Ta, Tu, E. The

alarm will begin based on the forecast temperatures or

with temperatures taking by a sensor in real time each

hour.

In the first case, the forecast temperatures for the

next 12 hours is calculated and their values are

compared with Ta+Tu. If they are under this value,

the risk index (RI) will have intensity equal to the

number of hours that this happens, so the maximum

value of RI is 12. In the case that RI is zero, the alarm

will not be active.

In the second case, a sensor is registering the real

temperature each hour and it is compared with Ta+Tu,

if it is lower then the alarm is active and RI will

increase in one each hour it happens. At the same time,

ME is calculated and compared with its threshold (E),

doing a similar decision: if ME is under E (remember

that it has a negative value), RI will increase in one

unit if not, RI=0.

FREEZING ALARM SYSTEM BASED ON TIME SERIES ANALISYS

361

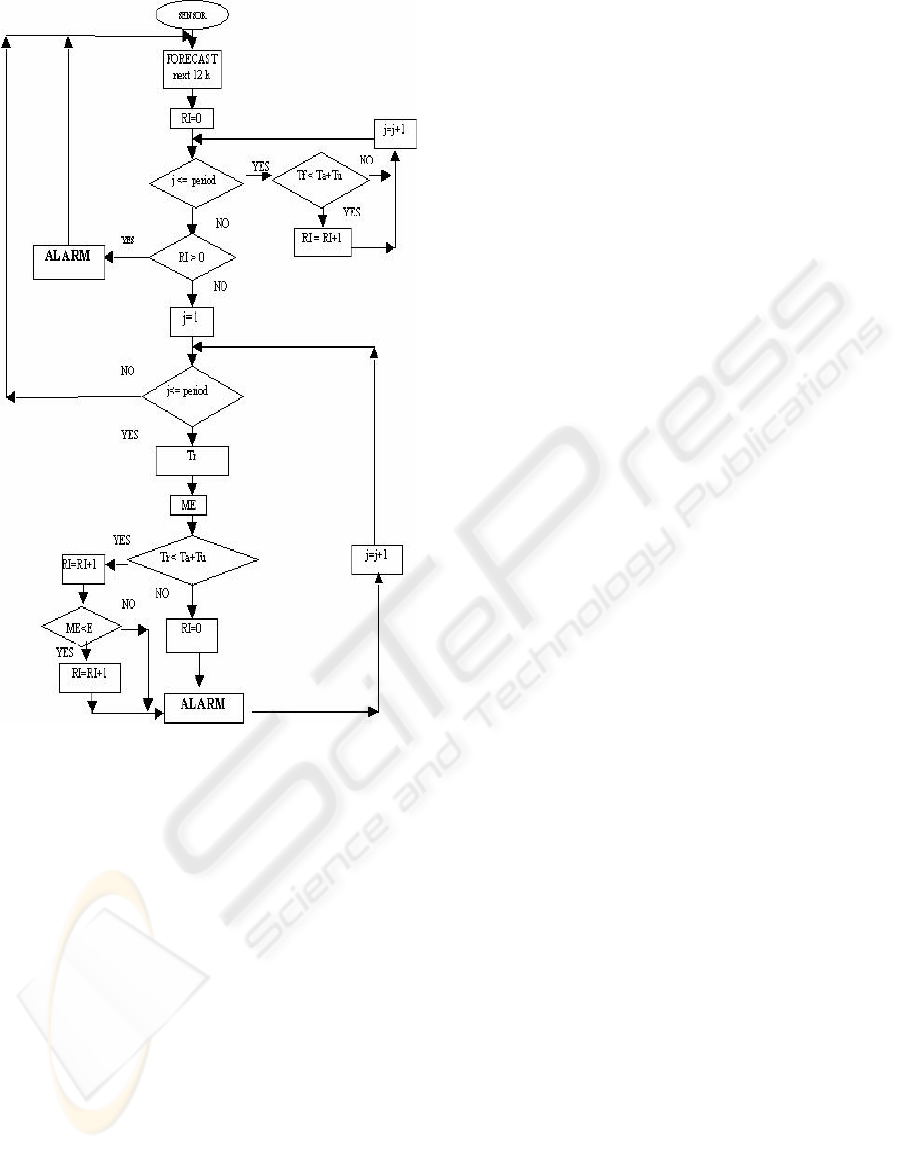
Figure 1: Alarm system flow chart

3 RESULTS AND CONCLUSIONS

The hourly temperature series from November to April

are analyzed and the forecast calculated each 12 hours.

Box-Jenkins methodology gives a useful model to

forecast each interval with a good result. The

confidence interval selected was 95% and the selected

model for all the series was (1,1,1), (1,1,1)

. This

model is autoregressive and with a moving average,

differentiated in the seasonal as in the non-seasonal

part. This indicates a dependency of the recent

temperatures and noise, as well as the temperatures

and noise from the last day (Carlson et al, 1970).

As an example, two last weak in March have been

showed (336 data points). This month has been

selected due to its high risk and crop damage that

normally are registered. Beside it, this month shows all

the possible cases to test the design of the system

alarm.

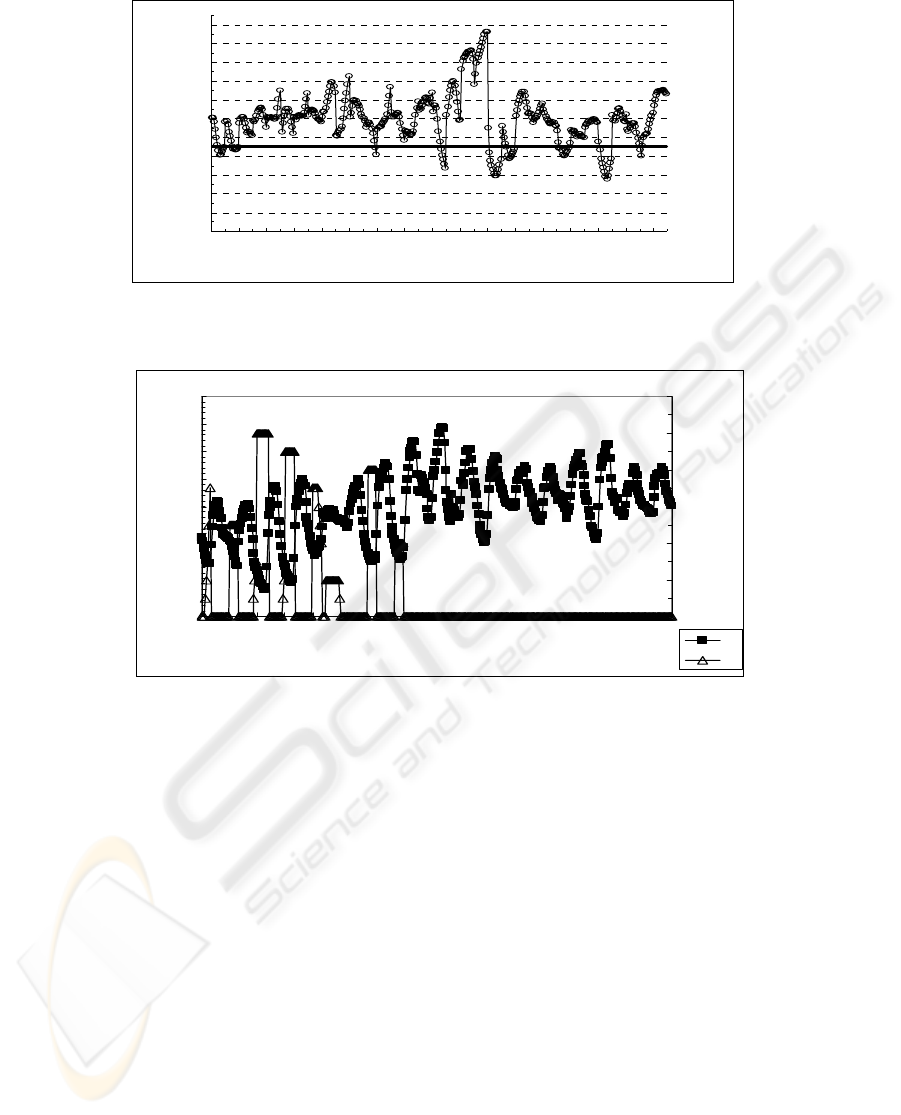
The hours that present a higher freezing risk are the

first hours of the interval time. Studying the ME

(figure 2) for these days we can see that the value

corresponding to –1.5 is the correct one to be selected

as a threshold (E). This value is obtained in all the

scenarios studied (data not showed) at this

meteorological station.

The alarm index (RI) is showed in figure 3. Its value

varies between 0 and 12, depending on the Tr and Tf

in each forecasted interval. The first case explained by

the algorithm corresponds to isolated points

(horizontal dimension 1), which begins with an index

of 1 or 2 and it can be increased with this pattern. The

second case corresponds to alarm indexes of high

value can achieve 12 and its horizontal dimension is

bigger than 1. This dimension indicates the

consecutive number of hours with a freezing risk and

this information is important in the possible crop

damage and its consequences in crop yield and quality.

In the same figure (figure 3) real temperatures are

showed to compare the alarm efficiency to detect the

high-risk intervals.

The control system of the alarm is useful. It allows to

detect with enough time periods where the

probabilities of freezing temperatures are high.

For all the months studied the alarm is activated

normally by the forecasted temperature, and in a few

cases by the real temperature without using Tf. Further

research is necessary to improve this alarm system, but

nor days reduce the freezing situations without a

previous risk notification so a prevention can be

applied.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

362

-6,0

-5,0

-4,0

-3,0

-2,0

-1,0

0,0

1,0

2,0

3,0

4,0

5,0

00000000000000000

Day time (h.)

Mean Error

Figure 2: Mean error values (ME) corresponding to the third and fourth week of March of 1996. Bold line corresponds to the

threshold mean error

-10,0

-5,0

0,0

5,0

10,0

15,0

20,0

25,0

30,0

00000000000000000

Day time (h.)

Tr (ºC)

Figure 3: Real temperature (Tr) and Risk index (RI) during third and fourth weak in March 1996

REFERENCES

Bowerman, B.L., O'Connell, R.T.; 1.987. Time Series

Forecasting. United Conceps and Computer

Implementation. Duxbury Press. Boxton. 2nd edition

Box, G.E.P., Jenkins, G.M. , 1970. Times series

Analysis:Forecasting and control. San Francisco:

Holden Day

Cao, W., and D.N. Moss. 1989. Temperature effect on leaf

and phyllochron in wheat and barley. Crop Science.

29(4):1018-1021.

Carlson, R.F.; Maccormick, J.A.; Watts, D.G., 1.970.

Application of Linear Random Models to four Annual

Steamflow Series. Water Resources Research. v.6, No.4,

pp 1070-1078.

Castellanos, M.T., 1997. Estudio y predicción de

temperaturas mediante análisis de series temporales en la

Comunidad de Madrid. Ph.D. Dissertation, Polytechnic

University of Madrid (UPM), Spain.

Fernandez, C.J., 1992. Simulation of normal annual and

diurnal temperature oscillation in non-mountainous

mainland Unites States. Agron. J. 84(2):244-251.

Jamieson , P.D. I.R. Brooking, J.R. Porter, and D.R. Wilson.

1995. Prediction of leaf appearance in wheat: a question

of temperature. Field Crops Research 41:35-44.

Kantz, H., and T. Schreiber. 1997. Nonlinear time series

analysis. Cambridge: Cambridge University Press.

Landau, S.; Mitchell, R.A.C.; Barnett, V.; Colls, J.J.;

Craigon, J. and Payne, R.W. 2000. A parsimonious,

multiple-regression model of wheat yield response to

environment. Agric.For. Meteorol., 101, 151-166.

Matalas, N.C.; 1.967. Times Series Analysis. Water

Resources Research. v.3, No.3, pp 817-829.

McMichael, F., and J. Hunter. 1972. Stochastic modeling of

temperature and flow in rivers. Water Resources

Research. 8, No.1,87-98.

Montgomery, A.L., and V. Zarnowitz.. 1998 . Time series

analysis: Unemployment-United States – forescasting.

Hornal of the American Statistical Association, 93,478-

492.

Noakes, D.J.; McLeod, A.I.; Hipel, K.W.; 1.985. Forecasting

Monthly Riverflow Times Series. International Journal

of Forecasting. v.1, pp 179-190.

FREEZING ALARM SYSTEM BASED ON TIME SERIES ANALISYS

363