GRASP FEASIBILITY COMPUTATION BASED ON CASCADING

FILTERS. APPLICATION TO A THREE FINGERED GRIPPER

Cesar Fernandez, M. Asuncion Vicente, Oscar Reinoso, Luis Paya, Rafael Puerto

Industrial Systems Engineering Department. Miguel Hernandez University

Av. Universidad s/n. 03202 Elche (Alicante), Spain.

Keywords:

Robot grasping, inverse kinematics, collision detection, optimization.

Abstract:

A simple, yet effective approach to grasp feasibility analysis is presented. The goal is to reduce the computa-

tional complexity of such process, whose complexity makes the detection of all feasible grasps for a certain

object unavoidable in most occasions. The approach is based on cascading ﬁlters of increasing complexity.

First, trivial ﬁlters are applied to all the grasp examples, thus rejecting all clearly unfeasible grasps with a small

computational effort. Then, more complex ﬁlters are applied to a reduced number of grasps and, at the end,

the full kinematics and collision detection analysis is only performed with a small subset of the grasps. An

example application is presented, where the goal is to detect all the possible 2D grasps of a certain object with

an articulated three-ﬁngered hand attached to a scara robot. The vertical axis is decoupled, thus resulting in a

highly redundant 7 DOF planar device. Simulation results are presented, where the reduction in computational

complexity is evaluated in terms of the number of ﬂoating point operations required. Such reduction can be as

high as 97% of the original computation time. An experimental setup has also been developed, with an indus-

trial scara robot and a speciﬁcally designed articulated three-ﬁngered gripper. The gripper has pneumatically

actuated opening and closing of the ﬁngers and electrically actuated abduction of the articulated ﬁngers. In

such experimental setup, the cascading ﬁlters approach shows a good behavior. Besides, the proposed system

can be easily adapted to different robot arms and hands.

1 INTRODUCTION

The goal of a robot grasp synthesis algorithm is to

select the best grasp for a certain object, given a ro-

bot arm and hand. The number of different grasps

that have to be analyzed can be extremely high, par-

ticularly when multiﬁngered grippers are used. In a

generic situation, a grasp is deﬁned as a set of n con-

tact points on the surface of the object, where n is

the number of gripper ﬁngers. Let us suppose that the

surface of the object can be deﬁned to a certain res-

olution by z 3D points. In such situation, there are





possible sets of contact points. If the gripper is

not symmetric, ﬁnger assignment is also relevant, so

each set represents n! different grasps, and the total

number of grasps can be expressed as N

in Eq. 1





· n! =

(z − n)!

(1)

Each of the N

possible grasps has to be analyzed

for feasibility. There are two main aspects that need

to be considered: ﬁrst, the kinematics of robot arm

and gripper; and second, the existence of collisions.

Concerning the ﬁrst aspect, the goal is to detect

whether the set of n points is reachable or not tak-

ing into account the root arm and gripper kinematics:

i.e. the goal is to solve the inverse kinematics. In

the general situation, there is a high level of redun-

dancy, and the computation of the inverse kinemat-

ics is thus very expensive. Only very simple grasp-

ing devices like two jaw parallel grippers are non-

redundant. Apart from that, there are several particu-

larities in grasp kinematics. First, there are multiple

end effectors, one per gripper ﬁnger, which are cou-

pled (some of the joints are common for several ﬁn-

gers); and second, desired conﬁgurations (end effec-

tor poses) are not strict in terms of orientation. This

remark is shown in ﬁgure 1, where two different sets

of end effector orientations reaching the same contact

points have to be considered valid and capable of per-

forming the grasp.

As it has been mentioned before, there is a sec-

ond aspect to be considered: the existence of colli-

181

Fernandez C., Asuncion Vicente M., Reinoso O., Paya L. and Puerto R. (2005).

GRASP FEASIBILITY COMPUTATION BASED ON CASCADING FILTERS. APPLICATION TO A THREE FINGERED GRIPPER.

In Proceedings of the Second Inter national Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 181-188

DOI: 10.5220/0001180401810188

 SciTePress

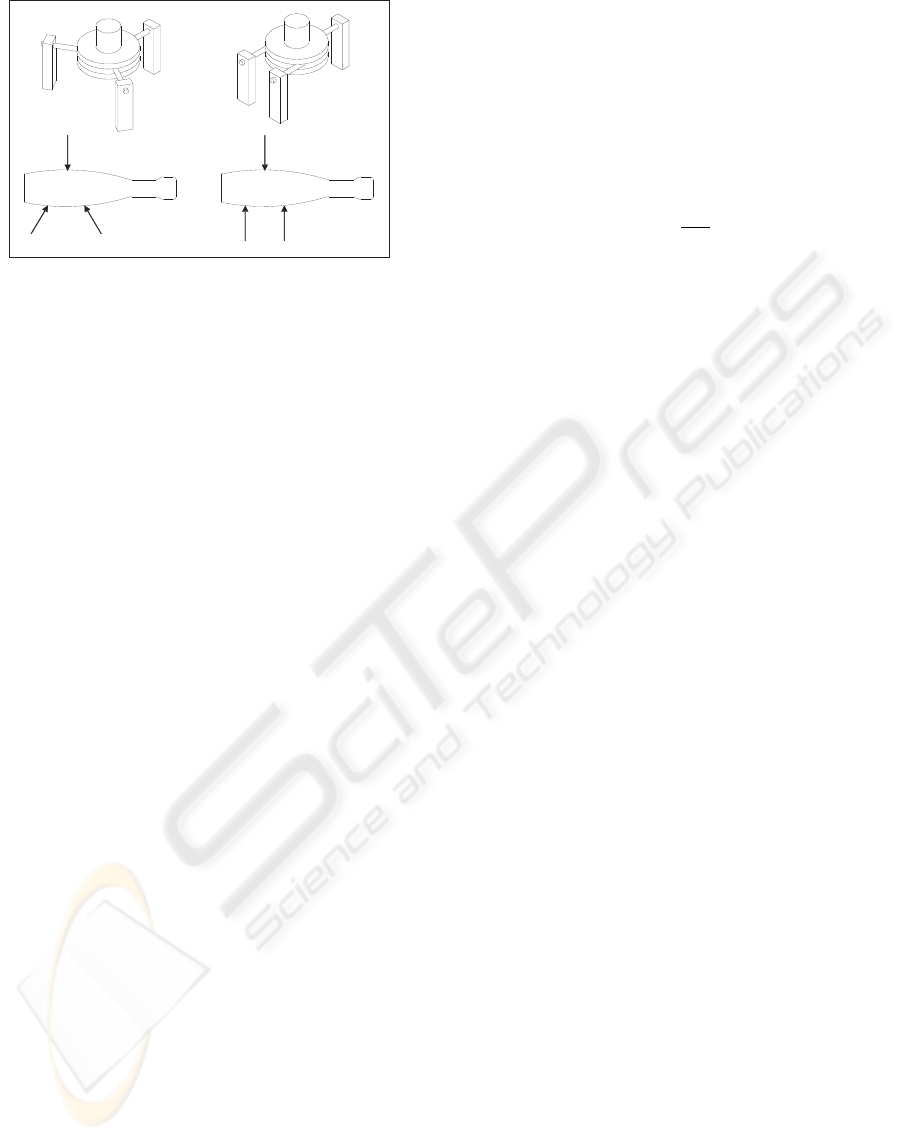
Figure 1: Orientation is not a strict restriction when comput-

ing the inverse kinematics of a grasp deﬁned by n contact

points.

sions. Even if the robot arm and gripper kinematics

allows to reach a certain set of n contact points, the

ﬁnal conﬁguration could produce collisions between

the object and the robot links (only the ﬁnal conﬁgu-

ration is taken into account as the problem of the path

followed by the robot gripper from the initial conﬁg-

uration is not addressed in this paper). The detection

of the possible collisions is also a computationally ex-

pensive problem.

In the present paper, a simple yet effective compu-

tational reduction technique is presented. Such tech-

nique is speciﬁcally designed for robot grasping, and

takes into account all the particularities of such prob-

lem.

The paper is structured as follows: section 2 de-

scribes the previous approaches to kinematic compu-

tation in the presence of redundancy and to collision

detection; and outlines their limitations for a robot

grasp application. Section 3 presents the proposed ap-

proach; and section 4 its application to a certain grasp

environment. Sections 5 and 6 present the results ob-

tained both in simulation and in a real experimental

setup. Finally, some conclusions are drawn on sec-

tion 7.

2 PREVIOUS APPROACHES TO

FEASIBILITY STUDY

Concerning the computation of the inverse kinemat-

ics in the presence of redundancy, multiple solutions

can be found in the literature. The easiest approach

is to add constraints for the redundant DOF; i.e. to

held ﬁxed a certain joint or to establish some ﬁxed re-

lationships between different joints. However, these

solutions are not valid when the goal is feasibility

computation: some of the available DOF are not ex-

ploited, and a grasp could be incorrectly classiﬁed as

unfeasible. Other approaches are based on the use

of iterative methods to approximate a good solution,

normally based on the Jacobian matrix J. In a gen-

eral case, when there are multiple end effectors (e.g.

grasping devices) the Jacobian matrix is deﬁned as in

Eq. 2, where p

denotes the i-th end effector position

(depending on the applications, p

can represent both

the end effector positions and orientations) and q

de-

notes the j-th robot joint.

J(Q) =



∂p

∂q



i,j

(2)

Inverse kinematics resolution based on the Jaco-

bian matrix can be accomplished in many differ-

ent ways: the Jacobian transpose method (Balestrino

et al., 1984)(Wolovich and Elliot, 1984), the Jacobian

pseudoinverse or null-space method (Baillieul, 1985),

the damped least squares method (Nakamura, 1986),

etc. However, these approaches are devoted to ﬁnd

a solution to the inverse kinematics and not to sim-

ply detect whether a solution exists; in this way, their

computational requirements could be reduced.

Other redundancy resolution methods are based on

parametric modelling rather than in the Jacobian ma-

trix. In (Dordevic et al., 2004), an approach based

on human motor control theories is presented. A tax-

onomy of robot motions is generated and, for each

motion example, the joint values are computed in an

off-line step called skill acquisition. When the robot

is requested to perform a certain motion, function ap-

proximators are used to interpolate the joint values

corresponding to the desired motion from the avail-

able skills. The main advantage of this method is its

low on-line computational complexity; but it is not

valid to detect the feasibility of a certain grasp. First,

it is devoted to robot motions; and second, a grasp

could be classiﬁed as unfeasible even if it could be

feasible using a conﬁguration different to that of the

stored skills.

Concerning the collision detection problem, multi-

ple algorithms have also been developed. When the

goal is collision free path planning, the conﬁguration

space (Lozano-Perez, 1983) is commonly used; how-

ever, the present paper is focused on the detection of

the collisions for the ﬁnal gripper conﬁguration, and

not on the path followed to reach such conﬁguration.

When the goal is the detection of collisions in a sta-

tic conﬁguration, most algorithms are based on the

representation of all the objects that could collide (ro-

bot links, object to be grasped and maybe surround-

ing obstacles) as sets of planar faces. The resolution

used for such representation is a key factor in obtain-

ing a good compromise between computational load

and accuracy of the results. A survey on collision de-

tection techniques can be found in (Jimenez et al.,

2001). There are multiple available optimized soft-

ware packages, like I-COLLIDE (Lin, 1993), RAPID

ICINCO 2005 - ROBOTICS AND AUTOMATION

182

(Gottschalk et al., 1996), V-COLLIDE (Hudson et al.,

1997), QUICK-CD (Klosowski, 1998), etc. In these

software packages, the goal is to detect precisely the

contact point or contact areas of a collision. Such in-

formation is not needed for feasibility computation; it

is just required to know whether there is a collision or

not.

3 PROPOSED APPROACH

The proposed approach is focused on feasibility com-

putation and not on computing the full inverse kine-

matics or detecting precisely the contact points of a

collision. In order to reduce the computational load,

cascading ﬁlters of increasing complexity are applied.

First, trivial ﬁlters are applied to all the grasp exam-

ples, thus rejecting all clearly unfeasible grasps with a

small computational effort. These trivial ﬁlters com-

pute absolute and relative distances for the n contact

points of the grasps and check whether the maximum

values, minimum values and ratios of such distances

fall within the valid ranges of robot arm and gripper.

Once this trivial ﬁlters have been applied and part

of the grasp candidates have been discarded, more

complex ﬁlters are applied to the remaining grasps.

This slightly more complex ﬁlters compute angular

measurements and trivial collision detection criteria

in order to reduce even more the number of grasp can-

didates. At this second step, the computational effort

required to test each grasp is higher but the number of

grasps to be checked is smaller as some of the candi-

dates were already ﬁltered in the ﬁrst step.

The complexity of the applied ﬁlters is increased at

each step, as the number of grasps examples where the

ﬁlters have to be applied is reduced. Finally, the most

complex ﬁlters (full kinematics analysis and collision

detection) are performed only in a very reduced sub-

set of examples. Figure 2 shows the cascading ﬁlters

structure.

Possible grasps

(N)

Filter

Feasiblegrasps

(Np)

…

P-1

REDUCTIONIN THENUMBEROFGRASPS TOBECHECKED

INCREASEOF THE FILTERS COMPLEXITY

Figure 2: Cascading ﬁlters: complexity increases as the

number of checks to be performed decreases.

The number of ﬁlters used is a key factor in the

reduction of complexity. Apparently, increasing the

number of ﬁlters should always result in a computa-

tional load decrease, provided the ﬁlters are chosen

wisely. However, the valid grasps (the ones not dis-

carded) have to be evaluated with all the ﬁlters. If

the number of ﬁlters is too high, computational load

could be increased instead: a compromise is required.

The cascading ﬁlters approach is particularly suited

to grasping applications, where multiple grasp candi-

dates have to be evaluated in order to choose the best

one. Each of the ﬁlters used have to be speciﬁc to a

certain robot arm and gripper, but the methodology

can be applied in general terms to all situations: the

most simple ﬁlters deal with distance measurements;

at a higher complexity level angular measurements

are considered; then trivial collision detection is per-

formed; and ﬁnally the full tests are carried out.

These full tests have to be slightly different to those

proposed in the literature, as the only requirement is

to detect whether a valid solution exist. Ad-hoc ﬁlters

should be developed depending on the application.

4 APPLICATION TO A

THREE-FINGERED GRIPPER

4.1 Deﬁnition of the example

application

The proposed approach has been applied to a robot

grasping environment. The goal is to detect all the

possible 2D grasps (planar grasps) that can be per-

formed with an articulated three-ﬁngered gripper at-

tached to a scara robot. The problem is analyzed in

2D so the vertical axis of the scara robot is decou-

pled. Figure 3 shows the planar kinematics of arm

and gripper.

Figure 3: Planar kinematics of the example application.

The system has a total of seven planar DOF, which

are clearly marked in the ﬁgure: three of them trans-

lational (opening and closing of the ﬁngers, which

are independent) and one rotational (abduction of the

two articulated ﬁngers, which are coupled). There is

a high redundancy, as a certain set of three contact

points can be reached with multiple conﬁgurations of

robot arm and gripper.

4.2 Selected ﬁlters

The ﬁlters used for the example application are de-

scribed in the next paragraphs. A total of ﬁve ﬁlters

GRASP FEASIBILITY COMPUTATION BASED ON CASCADING FILTERS. APPLICATION TO A THREE

FINGERED GRIPPER

183

have been deﬁned:

1. The ﬁrst ﬁlter measures the distance from the mid-

point of the three contact points to the robot origin.

Extremely large or extremely small distances result

in unfeasible grasps.

2. The second ﬁlter measures point to point distances

between the three contact points, and computes the

maximum value, the minimum value, the sum of

distances and the difference between maximum and

minimum values. All these measures have to fall

within the gripper range in order for the grasp to be

accepted.

3. The third ﬁlter measures the angle between the sur-

face normals at the three contact points: normals

that are too close to be parallel will be kinemat-

ically unfeasible or will result in a collision. A

threshold of 45 degrees is used.

4. The fourth ﬁlter computes the expected angle be-

tween the surface normals and the ﬁnger action

line. There are three possible ﬁnger assignments

for this gripper (three different ways of assigning

contact points to robot ﬁngers), and at least one of

the assignments must result in valid values for this

angle: a range of ± 45 degrees is allowed.

5. Finally, the ﬁfth ﬁlter computes a full kinematic

analysis and collision detection. As there is redun-

dancy, no closed solution for the inverse kinematics

can be found. To solve this problem, the range of

motion of one of the joints (abduction of the two

articulated ﬁngers) is discretized to a ﬁxed reso-

lution (100 values) and an analysis of kinematics

feasibility is performed for each abduction value.

The collision detection needs to be performed si-

multaneously: as the ﬁngers are supposed to have

planar surfaces, the expected contact points may be

slightly different to the real ones. In order to take

this effect into account, the previously computed

ﬁnger strokes are modiﬁed in order to avoid inter-

ferences between ﬁngers and object. If the ﬁnger

strokes are within valid ranges after the modiﬁca-

tion, the grasp is considered to be feasible. Even

though the computational load of this ﬁlter is not

very high, it is much more complex than the previ-

ous ﬁlters.

5 RESULTS IN SIMULATION

In order to check the validity of the proposed ap-

proach, a Matlab simulation environment has been

developed. This environment allows to represent any

2D robot arm and hand; for the experimental com-

parison, the scara robot and the three-ﬁngered gripper

described in section 4.1 are chosen. A database of 24

synthetic objects has been deﬁned, and a scale factor

has been applied to increase the variability of the ex-

amples: every object can have ﬁve different sizes, thus

resulting in a total of 120 different contours. Such

database is shown in ﬁgure 4.

Figure 4: Synthetic objects deﬁned for the simulation envi-

ronment.

During a simulation, a randomly chosen object is

presented in a random pose, which can be within

reach of the robot arm or not. The object contour is

discretized using an adjustable resolution and all the

feasible grasps are computed an displayed. Figures

5 and 6 show the process. Both a detailed view of

the object and a general view of its relative pose with

respect to the robot arm are displayed (bottom right

window of the image).

Figure 5: Simulation setup, ﬁrst step: an object is presented

in a random pose and its contour is discretized.

This simulation setup has also been used to test

a grasp synthesis algorithm (Fernandez et al., 2004)

ICINCO 2005 - ROBOTICS AND AUTOMATION

184

Figure 6: Simulation setup, second step: all the feasible

grasps are computed and displayed. Resolution has been

reduced in order to obtain a better visualization.

which, provided the feasible grasps have been com-

puted, selects the best one by similarity to grasp ex-

amples provided by the user and performs such grasp,

displaying the robot arm and gripper movements.

However, this paper is focused on the previous step:

the computation of the feasible grasps.

Such computation is performed following the cas-

cading ﬁlters approach presented in previous sections.

Figure 7 shows the behavior of the system over some

example objects belonging to the database: the num-

ber of grasps to be checked for feasibility gets smaller

as the ﬁlter complexity increases. The goal has been

achieved, as the relatively complex ﬁfth ﬁlter is only

evaluated in a small subset of grasps.

no filter 1 2 3 4 5

500

1000

1500

2000

2500

3000

3500

4000

4500

filter number

number of valid grasps

object 1

object 2

object 3

object 4

object 5

object 6

object 7

Figure 7: Simulation results: number of grasps remaining

after applying each ﬁlter.

1 2 3 4 5

1.5

2.5

3.5

4.5

filter number

log

(number of flops)

object 1

object 2

object 3

object 4

object 5

object 6

object 7

Figure 8: Simulation results: number of ﬂoating point oper-

ations required to perform each feasibility computation.

Concerning the computational complexity associ-

ated with each ﬁlter, ﬁgure 8 shows the number of

ﬂoating point operations required to perform each ﬁl-

ter computation. A logarithmic scale is used in the

y axis in order to be able to represent the high dif-

ferences in computational load between the different

ﬁlters; particularly, the ﬁfth ﬁlter is much more com-

plex than the others.

The combination of the results shown in ﬁgures 7

and 8 gives the total computational load. Table 1 com-

pares these results against the computational load as-

sociated with a direct application of the most complex

ﬁlter (full kinematics and collision analysis) to all the

possible grasps. It becomes clear that there are high

reductions in complexity, that range from 71% to 98%

(i.e. the proposed approach requires only the 2% of

the original computing time for certain objects).

Table 1: Comparison of computational complexity in terms

of ﬂoating point operations required to compute all the fea-

sible grasps for some example objects.

Object Cascading All tests Reduction

1 4.72 · 10

8.56 · 10

94.5%

2 8.03 · 10

4.39 · 10

81.7%

3 4.92 · 10

7.72 · 10

93.6%

4 1.12 · 10

2.33 · 10

95.2%

5 4.03 · 10

1.43 · 10

71.8%

6 4.59 · 10

2.29 · 10

98.0%

7 9.98 · 10

9.22 · 10

89.1%

6 RESULTS IN A

EXPERIMENTAL SETUP

A real experimental setup has also been used to check

the validity of the approach. An articulated three-

ﬁngered gripper has been designed and developed

GRASP FEASIBILITY COMPUTATION BASED ON CASCADING FILTERS. APPLICATION TO A THREE

FINGERED GRIPPER

185

speciﬁcally for these tests, following the structure of

the example application presented in section 4. It al-

lows independent ﬁnger strokes, with pneumatically

actuated opening and closing; and it has an extra DOF

which allows to modify the abduction of the two ar-

ticulated ﬁngers in the range 0 to 180 degrees. Such

abduction is electrically actuated by a DC motor. The

result is a highly redundant robot gripper. Figure 9

contains some drawings where the basic design and

the range of reachable abduction values is shown; ﬁg-

ures 10 and 11 show two images of the real device us-

ing different conﬁgurations to hold different objects.

In these ﬁgures, it becomes clear that the gripper has

been designed in order to be adaptable to objects of

different shapes. The basic structure of the Barret

hand (Bar, ) has been used as a guideline.

Figure 9: Design of the three-ﬁngered articulated hand and

range of abduction values.

Figure 10: Developed gripper: conﬁguration used to hold

objects with spherical shape.

The experimental setup includes also a Mitsubishi

RH-5AH55 scara robot where the gripper is attached

(details about such robot can be found in (Mit, )) and

a low cost Creative video camera (Cre, ) to detect the

contour of the objects to be grasped. Figure 12 shows

this environment. The camera is ﬁxed to the robot

arm, following an eye-in-hand conﬁguration. To ob-

tain the contour of the objects, a color-based region

growing algorithm is used, which grows the back-

Figure 11: Developed gripper: conﬁguration used to hold

objects with cylindrical shape.

ground region starting at one the image corners (uni-

form blue backgrounds and semi-controlled lighting

are used for the experiments). Afterwards, a set of 5

consecutive morphological closings are performed in

order to smooth the initial contours and discard irrel-

evant irregularities. All the image processing opera-

tions are performed using functions from the OpenCV

library (Ope, ). The results of the contour extraction

process on some example images are shown in ﬁgure

13. The system is robust enough to detect the contours

of most objects, even when highly reﬂective surfaces

are present.

Once the contours are extracted, they are dis-

cretized to a certain resolution and the cascading ﬁl-

ters approach is used to detect the feasible grasps.

In order to check the behavior of the system, both

the contour and the feasible grasps computed are dis-

played using a Matlab application similar to the one

used in the simulation setup. Figures 14 and 15 show

an example of contours extracted from a real object,

its discretization and the feasible grasps. A certain

level of noise is present in the extracted contour, but

the results are almost unaffected.

Figure 12: Experimental setup: robot arm and gripper and

video camera.

ICINCO 2005 - ROBOTICS AND AUTOMATION

186

Figure 13: Contours obtained for some example objects.

Finally, some experiments are performed with dif-

ferent objects in order to check the reduction of com-

putational load in the real environment. The same

structure used with the simulation setup is followed.

Table 2 and ﬁgures 16 and 17 show the results ob-

tained in terms of number of grasps kept after each

ﬁltering; computational load of each ﬁlter in ﬂoat-

ing point operations; and total computational load .

The efﬁciency of the proposed approach is conﬁrmed

as the reduction in computational complexity ranges

from 63% to 97%.

Figure 14: Experimental setup, ﬁrst step: an image is cap-

tured, and the object contour is extracted and discretized.

Figure 15: Experimental setup, second step: all the feasible

grasps are computed and displayed.

Table 2: Comparison of computational complexity in the

experimental setup.

Object Cascading All tests Reduction

1 4.94 · 10

1.05 · 10

95.3%

2 7.59 · 10

1.11 · 10

93.1%

3 1.04 · 10

3.89 · 10

97.3%

4 2.29 · 10

1.44 · 10

84.1%

5 4.63 · 10

1.27 · 10

63.4%

6 1.95 · 10

1.83 · 10

89.3%

7 1.79 · 10

1.02 · 10

82.5%

no filter 1 2 3 4 5

0.5

1.5

2.5

x 10

filter number

number of valid grasps

object 1

object 2

object 3

object 4

object 5

object 6

object 7

Figure 16: Experimental results: number of grasps remain-

ing after applying each ﬁlter.

GRASP FEASIBILITY COMPUTATION BASED ON CASCADING FILTERS. APPLICATION TO A THREE

FINGERED GRIPPER

187

1 2 3 4 5

1.5

2.5

3.5

4.5

5.5

filter number

log

(number of flops)

object 1

object 2

object 3

object 4

object 5

object 6

object 7

Figure 17: Experimental results: number of ﬂoating point

operations required to perform each feasibility computa-

tion.

7 CONCLUSIONS

Detecting all the feasible grasps for an object, given a

certain robot arm and hand, is a computationally ex-

pensive and normally unavoidable problem. Previous

research in this ﬁeld is devoted to optimize the res-

olution of the full inverse kinematics problem or to

optimize the detailed detection of collisions.

The approach presented in this paper allows to per-

form a fast feasibility study for all the possible grasps

of a certain object, computing the inverse kinemat-

ics and collision detection only in a reduced subset of

grasps.

Such approach can be adapted to any robot arm and

hand, as it has been shown with an example applica-

tion.

Experimental results performed both in simulation

and on a real environment show that the proposed ap-

proach allows high reductions in computational load.

Future work will be devoted to the application of

the proposed system in more complex grasping de-

vices (robot hands); and also to consider the existence

of collision free paths instead of the static collision

detection tests performed at present.

REFERENCES

Barret hand. <http://www.barretttechnology.com>.

Creative. <http://www.creative.com>.

Mitsubishi. <http://global.mitsubishielectric.com/bu/automation>.

Opencv. <http://www.intel.com/research/mrl/research/opencv>.

Baillieul, J. (1985). Kinematic programming alternatives

for redundant manipulators. In Proc. IEEE Int. Conf.

on Robotics and Automation, pages 722–728.

Balestrino, A., De Maria, G., and Sciavicco, L. (1984).

Robust control of robotic manipulators. In Proceed-

ings of the 9th IFAC World Congress, volume 5, pages

2435–2440.

Dordevic, G., Rasic, M., and Shadmehr, R. (2004). Para-

metric models for motion planning and control in bio-

mimetic robotics. IEEE Transactions on Robotics. (in

press).

Fernandez, C., Vicente, M. A., Reinoso, O., and Aracil, R.

(2004). A decision tree based approach to grasp syn-

thesis. In Proceedings of the International Conference

on Intelligent Manipulation and Grasping, pages 486–

491.

Gottschalk, S., Lin, M., and Manocha, D. (1996). A hier-

archical structure for rapid interference detection. In

Proc. of ACM Siggraph’96, pages 171–180.

Hudson, T., Lin, M., Cohen, J., Gottschalk, S., and

Manocha, D. (1997). V- collide: Accelerated colli-

sion detection for vrml. In Proc. of VRML Conference,

pages 119–125.

Jimenez, P., Thomas, F., and Torras, C. (2001). 3d colli-

sion detection: a survey. Computers and Graphics,

25(2):269–285.

Klosowski, J. (1998). Efﬁcient Collision Detection for In-

teractive 3D Graphics and Virtual Environments. PhD

thesis, University of New York.

Lin, M. (1993). Effcient Collision Detection for Animation

and Robotics. PhD thesis, University of California.

Lozano-Perez, T. (1983). Spatial planning: a conﬁguration

space approach. IEEE Transactions on Computers,

32(2):108–120.

Nakamura, Y. (1986). Inverse kinematics solutions with

singularity robustness for robot manipulator control.

Journal of Dynamic Systems, Measurements and Con-

trol, 108:163–171.

Wolovich, W. A. and Elliot, H. (1984). A computational

technique for inverse kinematics. In Proc. of the 23rd

IEEE Conf. on Decision and Control, pages 1359–

1363.

ICINCO 2005 - ROBOTICS AND AUTOMATION

188