REVERSIBILITY ENFORCEMENT FOR UNBOUNDED PETRI NETS

Hanife Apaydın

Ozkan and Aydın Aybar

Department of Electrical and Electronics Engineering, Anadolu University

26470 Eskis¸ehir, TURKEY

Keywords:

Petri nets, partially reversibility, reversibility, algorithms.

Abstract:

In this paper, partially reversibility property and reversibility enforcement are studied for unbounded Petri nets.

A method which tests partial reversibility, and also ﬁnds a bound vector guaranting reversibility for unbounded

Petri nets is developed and an algorithm of the method is generated. Furthermore a controller design approach

which enforces reversibility for unbounded Petri nets is introduced.

1 INTRODUCTION

Petri net model is a common tool for discrete event

systems. Some properties and deﬁnitions are used to

describe this model. Properties of Petri nets are de-

composed into two types such as behavioral and struc-

tural properties (Desrochers and Al-Jaar, 1995; Proth

and Xie, 1996). In this work, we consider reversibility

and partially reversibility which are two of important

behavioral properties of Petri nets.

Some approaches have been presented to analyse

reversibility and partially reversibility of Petri nets.

The most favor is constructing reachability set. But

it is not efﬁcient for unbounded Petri nets because of

inﬁnite number of reachable marking vectors (Peter-

son, 1981). If a Petri net is partially reversible for at

least one initial state, that is proven by using a struc-

tural analysis method named T-invariant (Desrochers

and Al-Jaar, 1995). The method which was developed

in (Jeng et al., 2002) veriﬁes reversibility for 1-place

unbounded Petri nets. Since these approaches give

sufﬁcient but not necessary conditions for partially re-

versibility, they do not propose a way to test partially

reversibility of all unbounded Petri nets.

In this work, reversibility enforcement is consid-

ered for unbounded Petri nets. It is possible to en-

force reversibility for a Petri net, if the net is par-

tially reversible. Hence, testing partially reversibility

is very important for our work. We present a method

to test partially reversibility for unbounded Petri nets.

If the net is partially reversible the method proposes

a bound vector covering all reachable markings in a

reversible subset of the reachability set. Moreover,

we explain the controller presented in (Aybar et al.,

2005) which enforces reversibility at each times it is

used with the bound vector proposed by our method.

2 PRELIMINARIES

2.1 Notations of Petri Nets

A Petri net is denoted by ﬁve tuple

G(P, T, N, O, m

), where P is the set of places, T is

the set of transitions, N : P × T → Z is the input

matrix that speciﬁes the weights of arcs directed from

places to transitions, O : P × T → Z is the output

matrix that speciﬁes the weights of arcs directed

from transitions to places, where Z is the set of

non-negative integer numbers, and m

is the initial

marking.

M : P → Z is a marking vector in other words

marking, M(p) indicates the number of tokens as-

signed by marking M to place p. A transition t ∈ T

is enabled if and only if M(p) ≥ N(p, t) for all

p ∈ P . A ﬁring sequence g is a sequence of enabled

transitions t

. . . t

, where t

, t

, . . . , t

∈ T . A

marking M

′

is said to be reachable from M if there

exists a ﬁring sequence starting from M (i.e., the ﬁrst

transition of the sequence ﬁres at M) and yielding

′

(i.e., the ﬁnal transition of the sequence yields

′

). The set denoted by R(G, M ) is the set of all

marking vectors reachable from M . R(G, m

) is

181

Apaydın Özkan H. and Aybar A. (2005).

REVERSIBILITY ENFORCEMENT FOR UNBOUNDED PETRI NETS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 181-186

DOI: 10.5220/0001180501810186

 SciTePress

called as reachability set of the Petri net. We let

E(G, M) to denote the set of transitions which are

enabled at M ∈ R(G, m

). For a Petri net, we also

let ρ(M, g) to denote the transition function, which

gives the yielded marking when the sequence g ﬁres

starting from M (ρ is in fact a partial function, since

it is not deﬁned if g contains transitions which are not

enabled) (Aybar and

Iftar, 2003). If M

′

= ρ(M, g),

then M

′

= M + (O − N)U = M + AU. Here; M

and M

′

are markings, N and O are input and output

matrices respectively, A := O − N is incidence

matrix and U : T → Z is ﬁring count vector whose

jth element indicates how many times t

is ﬁred in g.

Let us remember some behavioral properties

related to the discussion of this work. G is said

to be K-bounded, if M (p) ≤ K(p), ∀p ∈ P ,

∀M ∈ R(G, m

) (K : P → Z), G is said to be

bounded if it is K-bounded for some K : P → Z.

Otherwise G is unbounded. G is said to be reversible

if m

∈ R(G, M), ∀M ∈ R(G, m

). G is said

to be partially reversible if m

∈ R(G, M ) for at

least one M ∈ R(G, m

) such that M 6= m

. Note

that, if a Petri net is partially reversible, there exists

a reversible subset of R(G, m

) and it is possible

to ﬁnd a bound vector covering all markings in this

subset. It is possible to enforce reversibility of the net

by using this bound vector with the controller in (Ay-

bar et al., 2005). Therefore, we say that this bound

vector guarantees reversibility for the considered net.

Deadlock is said to occur in a Petri net if there exists

M ∈ R(G, m

) such that no transition t ∈ T can

ﬁre at M (Desrochers and Al-Jaar, 1995). A marking

M covers a marking M if

M(p) ≥ M (p), ∀p ∈ P .

A marking

M dominates a marking M , if

M covers

M and M 6=

M. That is denoted by

M >

M and E(G, M) = E(G,

M), then

ρ(

M, t) >

ρ(M, t), ∀t ∈ E(G, M) (Cassandras

and Lafortune, 1999).

The behavioral properties of Petri nets are com-

monly explained by using reachability set. Since

unbounded Petri nets have inﬁnite number of reach-

able markings, the coverability tree (CT) is used to

analyse some behavioral properties instead of the

reachability set. CT is drawn as a tree, where each

node of tree either explicitly represents a reachable

marking of m

or covers a reachable marking of m

through w notation. If there exists a w notation at a

place of a marking in the CT, this place is unbounded

place and this Petri net is unbounded (Desrochers and

Al-Jaar, 1995). Note that since the representation of

an inﬁnite set is ﬁnite, an inﬁnite number of markings

must be mapped onto the same representation in the

CT.

In this paper an algorithm in (Zhou and DiCe-

sare, 1993) (Algorithm 5.1 on page 104) is used to

construct CT.

3 REVERSIBILITY FOR

UNBOUNDED PETRI NETS

Some works have been presented about reversibility

of Petri nets (Peterson, 1981; Desrochers and Al-Jaar,

1995; Jeng et al., 2002). But none of them has abil-

ity of testing partially reversibility of unbounded Petri

nets.

In this section we will explain a method, called Par-

tially Reversibility Testing Method (PRTM). PRTM

tests partially reversibility of unbounded Petri nets

and yields a bound vector guaranting reversibility for

the considered net. To facilitate discussion of the

method, we ﬁrst give the following explanations and

Lemma 1.

Let R

′

be a set of marking vectors such that R

′

{M ∈ R(G, m

) | ρ(M, t) = m

, t ∈ T } then

M(p) = m

(p) ± a, a ∈ {0, 1...ν

}, ∀p ∈ P . This

means ∀M ∈ R

′

, M(p) ≤ m

(p) + ν

, ∀p ∈ P .

Here ν

denotes the maximum number of token vari-

ation in place p by ﬁring any enabled transition. It can

be determined for each place p ∈ P by the following

way:

= max

t∈T

(N(p, t), O(p, t)) (1)

Note that, if M(p) > m

(p) + ν

for at least one

p ∈ P , then M 6∈ R

′

Lemma 1: If there exists a marking M ∈ R

′

such

that M 6= m

, Petri net is partially reversible. Other-

wise, Petri net is not partially reversible.

Proof: In a Petri net, each of the marking vector

M satisﬁying ρ(M, t) = m

are the members of

the set R

′

. So, if there exists M ∈ R

′

such that

M 6= m

, Petri net is partially reversible. If there

exists no M ∈ R(G, m

) such that ρ(M, t) = m

and M 6= m

(there exists no marking M ∈ R

′

such

that M 6= m

), then there exists no

M ∈ R(G, m

)

such that ρ(

M, g) = m

. Hence Petri net is not par-

tially reversible. ⋄

Although we do not know the reachability set for

unbounded Petri nets; as a result of Lemma 1, we

know that R

′

must have a marking vector other than

for the presence of partially reversibility. There-

fore, it is efﬁcient to determine only R

′

set of the

Petri net to test partially reversibility and one does

not need to construct all reachability set for this test.

PRTM tests partially reversibility of the considered

unbounded Petri net by using this fact. It is possi-

ble to ﬁnd a bound vector guaranting reversibility for

a Petri net, iff the net is partially reversible. Hence,

PRTM proposes a bound vector guaranting reversibil-

ity, if the considered net is partially reversible.

At the ﬁrst step, PRTM determines unbounded

places of the Petri net by using the CT and begins

obtaining reachable markings from m

by ﬁring tran-

sitions. In fact, for any unbounded Petri net it is

ICINCO 2005 - ROBOTICS AND AUTOMATION

182

possible to construct sets of reachable markings such

that markings in each set are obtained by ﬁring tran-

sitions or transition sequences from markings in the

one previous generated set and each marking in each

set dominates one of the marking in the one previous

generated set (Cassandras and Lafortune, 1999). The

method determines these sets (R

, R

...) step

by step. When it ﬁnds a set R

such that ∀M ∈ R

there exists a ˜p ∈

P (

P denotes the set of unbounded

places) such that M(˜p) > m

(˜p) + ν

˜p

, this means

∩R

′

= ∅. Then, the method obtains a set

R includ-

ing all of the markings obtained from m

to that point,

i.e

R =

i−1

j=0

. Since ∀i ∈ {1, 2, ...}, each of the

markings in R

i+1

will dominate one of the marking

in R

, R

′

of the Petri net is a subset of

R and it is

determined by searching the markings M ∈

R such

that ρ(M, t) = m

. If there exists a marking M ∈ R

′

such that M 6= m

, this Petri net is partially reversible

(see, Lemma 1) and PRTM proposes a bound vector

covering all of the markings in

R for guaranting re-

versibility of the Petri net. Otherwise, Petri net is not

partially reversible (see, Lemma 1) and it is impossi-

ble to guarantee reversibility. Hence, the method does

not propose any bound vector.

3.1 Algorithms

In this section, the algorithm for PRTM, which is

explained in Section 3, is presented with the help of a

motivation example.

The main algorithm for PRTM is named

Main[G, M] (see, Appendix A). In this algo-

rithm; ﬁrst the set of unbounded places of a Petri

net is determined by the function

P = C

(G)

which ﬁnds the set of unbounded places (

P ) of

Petri net by constructing CT; for the Petri net

shown in Figure 1, the set of vectors in the CT is

{[2 1 0]

, [1 2 1]

, [3 0 0]

, [0 3 2]

, [2 1 w]

[1 2 w]

, [3 0 w]

, [0 3 w]

} and

P = {p

}. Then

the set R

′

of Petri net is determined by the algorithm

Rprime[G, M,

P ]. If there exists M ∈ R

′

such

that M 6= m

, Petri net is partially reversible and

a bound vector guaranting reversibility of the net

is determined. Otherwise Petri net is not partially

reversible (see, Lemma 1) and the algorithm is halted.

Main[G, M] algorithm calls Rprime[G, M,

P ] to construct R

′

set of Petri net (see, Appendix A).

At this algorithm, the sets R

, R

, ... are the sets of

markings and each of these sets are obtained by ﬁring

transitions or transition sequences from markings in

the previous set. Each marking in each set dominates

one of the marking in the one previous set, i.e, R

i+1

is obtained by ﬁring transitions from R

, and each of

the markings in R

i+1

dominates one of the marking

in R

, i ∈ Z. For the construction of these sets;

Figure 1: Motivation example (Proth and Xie, 1996)

Figure 2: Obtained markings of Petri net in Figure 1

ﬁrst, all enabled transitions are ﬁred from m

. This

leads new markings. The new markings which are

previously generated are labeled as old. The new

markings which are deadlock are labeled as dead. If

on the path

M = ρ(m

, g) (path from m

to a new

marking

M), there exists a marking M such that,

M >

M, and E(G, M) = E(G,

M), then

M is la-

beled as root (ρ(

M, t) >

ρ(M, t), ∀t ∈ E(G, M)).

From markings which are not labeled as old, dead

or root, we continue ﬁring transitions and obtain

new markings. If all of the enabled transitions of a

marking are ﬁred, this marking is labeled as cnt. This

process is proceed until there exists no nolabeled

markings. Then, except old labeled markings, all

of the markings obtained from m

at this process

construct the set R

and the root labeled markings in

construct the set SM

. Then a new cycle begins

by ﬁring enable transitions of each markings in SM

As before, until there exists no nolabeled marking,

new markings are obtained and they are labeled. But

after that point rule of labeling as root changes: a

new marking

M is labeled as root if there exists a

marking M in the set SM

such that,

M >

and E(G, M) = E(G,

M). Then, except old labeled

markings, all the markings obtained from SM

this process construct the set R

and the root labeled

markings in R

construct the set SM

. If ∀M ∈ R

REVERSIBILITY ENFORCEMENT FOR UNBOUNDED PETRI NETS

183

there exists a ˜p ∈

P such that,

M(˜p) > m

(˜p) + ν

˜p

, (R

∩ R

′

= ∅) (2)

all of the markings in the set R

(i > 1) also sat-

isfy equation (2). This means, none of the mark-

ings which will be obtained can not be a new mem-

ber of the set R

′

of Petri net. Then a set

R (R

′

⊂

R) is obtained, i.e.

R = R

, and the set R

′

of Petri net is determined by searching the mark-

ings in

R satisfying ρ(M, t) = m

, t ∈ T . For

the motivation example, the set R

is determined as

{[2 1 0]

, [1 2 1]

, [3 0 0]

, [0 3 2]

, [2 1 1]

[1 2 2]

, [3 0 1]

} (see, Figure 2). Since some

markings in the set R

do not satisfy equation

(2), i.e [2 1 1]

; from markings in the set R

a new set is constructed as R

= {[0 3 3]

[1 2 3]

, [3 0 2]

, [2 1 2]

} (see, Figure 2). Note

that, each of the markings in R

dominates one of the

marking in R

. Since all markings in R

satisfy equa-

tion (2),

R = R

. By searching the markings M in

R such that ρ(M, t) = m

, the set R

′

is obtained as

′

= {[1 2 1]

} for the Petri net shown in Figure 1.

If some of the markings of R

of a Petri net do not

satisfy equation (2), from each markings in SM

their

enabled transitions are ﬁred. By this way, new mark-

ings are obtained and the sets SM

and R

are con-

structed (except old labeled markings, all of the mark-

ings obtained from markings in SM

at this process

construct the set R

and the root labeled markings

in R

construct the set SM

). This process is proceed

until a set R

satisfying equation (2) is obtained. Then

a set

R (R

′

⊂

R) is obtained, i.e.

R =

i−1

j=0

, and

the set R

′

of Petri net is determined by searching the

markings in

R such that ρ(M, t) = m

If there exists M ∈ R

′

such that M 6= m

, Petri net

is partially reversible and Main[G, M] algorithm de-

termines a bound vector K covering all of the mark-

ings in

R and guaranting reversibility of Petri net. For

the motivation example, the set R

′

is determined as

{[1 2 1]

}. Since [1 2 1]

6= m

, Petri net is par-

tially reversible. The set of markings including all of

the markings on the path ρ(m

, g) = [1 2 1]

is a

reversible subset of the reachability set. Since

R in-

cludes this set, the bound vector [3 3 2]

covering all

markings in

R guarantees reversibility of this net.

If there exists no M ∈ R

′

such that M 6= m

Petri net is not partially reversible and any bound vec-

tor is not determined by the algorithm Main[G, M ].

Because, there exists no M ∈ R(G, m

) such that

ρ(M, g) = m

, if a Petri net is not partially reversible.

Therefore, any K can not guarantee reversibility of

the net.

Theorem 1: The bound vector K obtained by the al-

gorithm Main[G, M] guarantees reversibility for un-

bounded Petri net G.

Proof: If a marking M such that M 6= m

is a mem-

ber of R

′

, then Petri net is partially reversible and a

bound vector K is determined. Since K covers not

only all of the markings in R

′

but also all of the mark-

ings on the path from m

to each markings in R

′

covers all of the markings in

R), it covers all of the

markings in a reversible subset of the reachability set

of the Petri net and it guarantees reversibility. ⋄

4 A CONTROLLER TO ENFORCE

REVERSIBILITY

In (Aybar et al., 2005), some algorithms and a con-

troller have been presented to enforce boundedness,

reversibility and liveness. In that work; initially, with

an arbitrarily chosen bound vector, a bounded reach-

ability set of an unbounded Petri net has been deter-

mined; then, the reversible subset of that bounded set

is constructed by using developed algorithms. Since

obtained reversible set may be empty, reversibility can

not be enforced by the controller everytimes.

If the considered unbounded Petri net is partially

reversible, PRTM presented in the Section 3 obtains

a bound vector, K, which guarantees reversibility for

unbounded Petri nets. By running the developed algo-

rithms in (Aybar et al., 2005) with the obtained bound

vector gives a reversible subset of the reachability set

of considered unbounded Petri net. So it is possible

to enforce reversibility for this net by using controller

presented in (Aybar et al., 2005). In this section that

controller will be explained.

If a bound vector K is obtained by PRTM, Petri

net is partially reversible and it is possible to enforce

reversibility for this net by a controller. K bounded

reachability set is found by the algorithm named

Bounded-Set (Aybar et al., 2005), i.e. RB=Bounded-

Set(G, K). Here, K and G are the inputs of the algo-

rithm and represent the bound vector and deﬁnition of

the Petri net, respectively; RB is the output of the al-

gorithm and represents K bounded reachability set of

G. Reversible subset of RB is found by the algorithm

named Reversible-Set, i.e. Rr=Reversible-Set(RB)

where R

is the reversible subset of RB. Note that,

since K guarantees reversibility, R

6= ∅. Then, it

is known that if a Petri net is partially reversible, the

controller c(M, t) below enforces boundedness and

reversibility of the net (Aybar et al., 2005).

c(M, t) =



1, if ρ(M, t) ∈ R

0, otherwise

(3)

where, M ∈ R(G, m

), t ∈ E(G, M). If c(M, t) =

1, then ρ(M, t) ∈ R

and ﬁring transition t from

marking M is allowed. If c(M, t) = 0, then

ρ(M, t) /∈ R

and ﬁring transition t from marking

M is forbidden.

ICINCO 2005 - ROBOTICS AND AUTOMATION

184

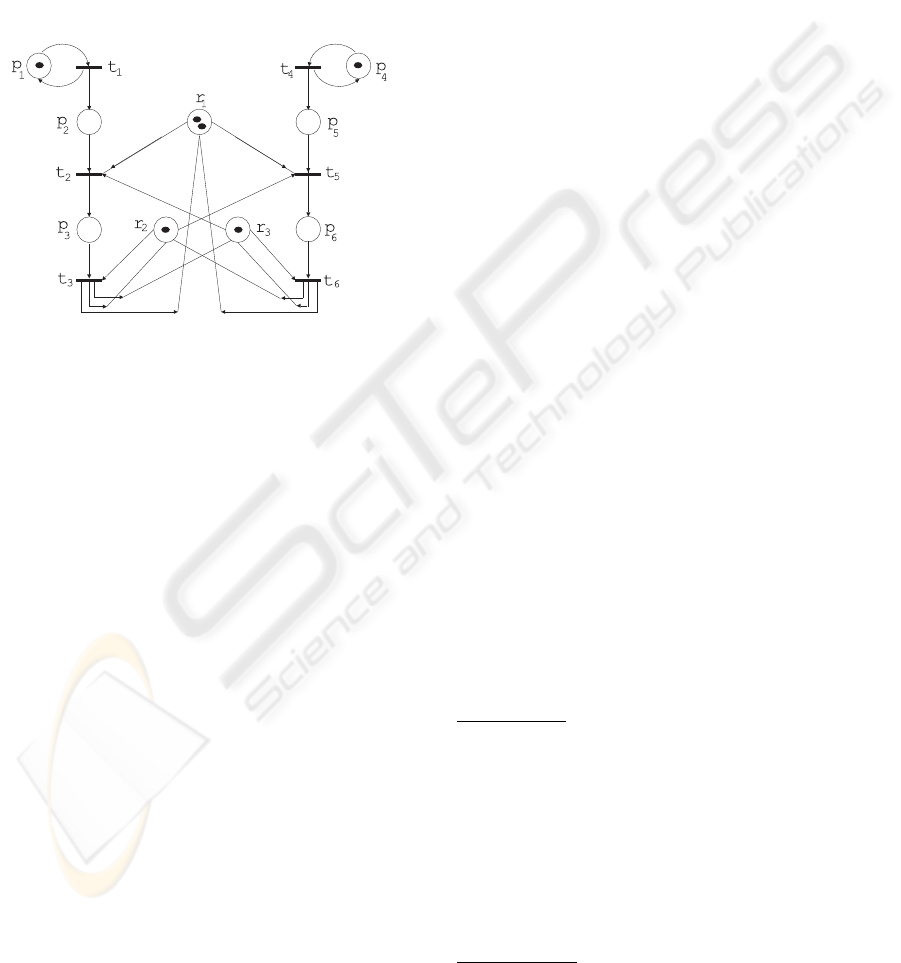
5 EXAMPLE

Let us consider a Petri net modelled manufacturing

system borrowed from (Proth and Xie, 1996) as an

example. The Petri net model of this system is pre-

sented in Figure 3. Since the weights of arcs are unity,

= 1, ∀p ∈ P . For this Petri net, the set of places

P = {p

, p

, r

, p

}, the set of

transitions T = {t

, t

}, and the initial

marking is m

= [1 0 0 2 1 1 1 0 0]

. At the ﬁrst step,

Figure 3: Example Petri net.

the algorithm Main[G, M] calls the function C

(G)

to ﬁnd the unbounded places. Since there exists w

notation at some places (p

, p

) of some markings at

CT of this Petri net (Apaydın-

Ozkan, 2005), the set of

unbounded places of this net is

P = {p

, p

}. Then

Main[G, M] calls the algorithm Rprime[G, M,

P ]

to obtain a set including R

′

set of Petri net and R

′

it-

self. For this purpose ﬁrst R

then R

are obtained

(|R

| = 16, |R

| = 41, here | ∗ | denotes the number

of elements of set “∗”). Since R

does not satisfy

equation (2), process continues and R

is obtained

(|R

| = 63). ∀M ∈ R

, R

satisﬁes equation (2).

This means, R

∩ R

′

= ∅ and all the members of

′

are obtained (R

∩ R

′

= ∅, i ∈ {2, 3, 4, 5...}).

Then a set

R including R

′

of Petri net is obtained as

R = R

∪ R

R| = 57). Through the markings in

the set

R, only markings M

= [1 0 1 1 1 0 1 0 0]

and M

= [1 0 0 1 0 1 1 0 1]

reach to m

by ﬁring only one transition, i.e. ρ(M

, t

) =

, ρ(M

, t

) = m

. Hence, R

′

is determined as

, M

}. Since there exist some M ∈ R

′

such

that M 6= m

6= m

, M

6= m

), Petri net

is partially reversible and Main[G, M] determines

the vector K = [1 4 1 2 1 1 1 4 1]

covering

all of the markings in the set

R. The bounded set

RB, which is obtained by RB=Bounded-Set(G, K),

is partially reversible and the reversible set R

, which

is obtained by Rr=Reversible-Set(RB), is not empty

(|RB| = 100, |R

| = 75)

. As a result, ob-

tained K guarantees reversibility of the Petri net. Ad-

ditionally the controller c(M, t) enforces not only

boundedness but also reversibility for this net. If

we were to give two speciﬁc cases as an exam-

ple, c([1 2 0 2 1 1 1 2 0]

, t

) = 1 since

ρ([1 2 0 2 1 1 1 2 0]

, t

) = [1 3 0 2 1 1 1 2 0]

∈

; c([1 4 0 1 0 1 1 4 1]

, t

) = 0 since

ρ([1 4 0 1 0 1 1 4 1]

, t

) = [1 4 0 1 0 1 1 5 1]

/∈ R

6 CONCLUSION

In this work, we consider partially reversibility and re-

versibility enforcement for unbounded Petri nets. For

this purpose, a method and its corresponding algo-

rithm is developed. By using the algorithm, it is deter-

mined whether considered unbounded Petri net is par-

tially reversible or not. If it is partially reversible, the

algorithm determines a bound vector guaranting re-

versibility and the controller c(M, t) enforces bound-

edness and reversibility of this net. If the Petri net

is not partially reversible, algorithm does not ﬁnd a

bound vector and reversibility can not be enforced for

this Petri net.

In this work, a Matlab program is also developed to

simulate the presented algorithm.

Further research is underway to use T-invariants

(see, section 5.6 in (Desrochers and Al-Jaar, 1995))

for testing partially reversibility and reversibility en-

forcement of Petri nets. Only the Petri nets with con-

trollable transitions are the subjects under the discuss

in this work, this approach may be extended to Petri

nets with controllable and uncontrollable transitions.

APPENDICES

A) Algorithms for PRTM

Main [G,M]

P = C

[G];

R, R

′

>=Rprime[G, p

];

If (6 ∃M ∈ R

′

such that

M 6= m

) Then

“Petri net is not partially reversible”

Exit Main

Else

“Petri net is partially reversible”

For ( i = 1 : |P |)

K(i) = max

M∈

(M([P ]

));

End

The sets R

, R

, RB and R

of the example Petri

net are not given here due to space limitations. But one can

see them in (Apaydın-

Ozkan, 2005).

REVERSIBILITY ENFORCEMENT FOR UNBOUNDED PETRI NETS

185

End

Return K

Rprime[G, M,

P ]

i = 0; SM

= ∅;

For each ˜p ∈

P determine ν

˜p

;

Do loop Rtilde

If (

i=0

) Then

;

Else

=SM

i−1

;

End

Do loop R

set

Select a nolabeled marking M from R

;

If (M

is previously generated

) Then

Label M as old; R

= R

\{M};

Else If (E(G, M) = ∅) Then

Label M as dead;

Else If (i = 0 && ∃

on the path from

such that

M >

E(G, M) = E(G,

M))Then

Label M as root; SM

= SM

∪ {M};

Else If (i > 0 && ∃

M ∈ SM

i−1

such that

M >

M E(G, M) = E(G,

M)) Then

Label M as root; SM

= SM

∪ {M};

Else

Fire each transition in E(G, M) from M;

Add each obtained marking vector to set R

;

Label M as cnt;

End

If (6 ∃

nolabeled marking in

) Then

If (i 6= 0)Then

= R

\SM

i−1

;

End

Exit R

set

End

LoopR

set

If (∀M ∈ R

∃˜p

such that

M(˜p) > m

(˜p) + ν

˜p

) Then

R =

i−1

j=0

;

Exit Rtilde

End

i = i + 1;

= ∅; SM

= ∅;

Loop Rtilde

For (i = 1 : |

R|)

If (∃ t ∈ T

such that

ρ([

, t) = m

) Then

′

= R

′

∪ [

;

End

Return R

′

B) Notation used in the presentation of algoritms:

For a set X, |X| denotes the number of elements of

set X and [X]

denotes the ith element of X (i =

1, 2, ..., |X|). All the sets are assumed to be ordered.

If a new element is added to a set size m, the new

element is taken as the (m + 1)th element of the set.

∪ is used to set union. If a vector X dominates a

vector Y , X >

Y denotes this situation. M(p

denotes the ith place of marking M. The logic “and”

operation is represented by && in the algorithms.

REFERENCES

Apaydın-

Ozkan, H. (2005). Determination of bound vectors

to guarantee reversibility for unbounded Petri nets.

M.S Thesis. (in Turkish). Anadolu

Universitesi, Fen

Bilimleri Enstit

u, Eskis¸ehir, Turkey.

Aybar, A. and

Iftar, A. (2003). Decentralized controller de-

sign to enforce boundedness, liveness and reversibility

in Petri nets. In Proceeding CD-ROM of the European

Control Conference, Cambridge, UK.

Aybar, A.,

Iftar, A., and Apaydın-

Ozkan, H. (2005). Cen-

tralized and decentralized supervisory controller de-

sign to enforce boundedness, liveness and reversibil-

ity in Petri nets. International Journal of Control,

78:537–553.

Cassandras, C. G. and Lafortune, S. (1999). Introduction to

Discrete Event Systems. Kluwer Academics, Norwell,

MA.

Desrochers, A. A. and Al-Jaar, R. Y. (1995). Applications of

Petri Nets in Manufacturing Systems. The Institute of

Electrical and Electronics Engineers Inc., New York.

Jeng, M., Xie, X., and Peng, M. (2002). Process nets with

resources for manufacturing modeling and their analy-

sis. IEEE Transactions on Robotics and Automation,

18:875–889.

Peterson, J. (1981). Petri Net Theory and the Modeling of

Systems. Englewood Cliffs, NJ : Prentice-Hall, New

Jersey.

Proth, J. and Xie, X. (1996). Petri Nets: A Tool for Design

and Management of Manufacturing Systems. John Wi-

ley & Sons, West Sussex.

Zhou, M. and DiCesare, F. (1993). Petri Net Synthesis

for Discrete Event Control of Manufacturing Systems.

Kluwer Academic, Norwell, MA.

ICINCO 2005 - ROBOTICS AND AUTOMATION

186