
METHOD TO IMPROVE THE TRANSPARENCY OF
NEUROFUZZY SYSTEMS
J.A. Dom
´
ınguez-L
´
opez
Centro de Investigaci
´
on en Matem
´
aticas (CIMAT)
Callejon de Jalisco s/n, Guanajuato CP36240, MEXICO
Keywords:
Fuzzy control, neurofuzzy systems, transparency, learning, curse of dimensionality.
Abstract:
Neurofuzzy systems have been widely applied to a diverse range of applications because their robust operation
and network transparency. A neurofuzzy system is specified by a set of rules with confidences. However, as
knowledge base systems, neurofuzzy systems suffer from the curse of dimensionality i.e., exponential increase
in the demand of resources and in the number of rules. So, the interpretability of the final model can be lost.
Thus, it is desired to have a simple rule-base to ensure transparency and implementation efficiency. After
training, a rule can have several non-zero confidences. The more number of non-zero confidences, the less
transparent the final model becomes. Therefore, it is elemental to reduce the number of non-zero confidences.
To achieve this, the proposed algorithm search for (a maximum of) two non-zero confidences which give the
same result. Thus, the system can keep its complexity with a better transparency. The proposed methodology
is tested in a practical control problem to illustrate its effectiveness.
1 INTRODUCTION
Neurofuzzy systems have been successfully applied
to a diverse range of applications because they com-
bine the well-established modelling and learning ca-
pabilities of neural networks with the transparent
knowledge representation of fuzzy systems. The
fuzzy system is defined as a neural network type
structure keeping its fundamental components. In this
way, a fuzzy system can be derived from data or im-
proved by learning from interaction with the environ-
ment. After training the neurofuzzy network, the final
model is represented by the rule-base, which consists
of N rules of IF-THEN form. A specific rule effec-
tively describes the input-output relation of the sys-
tem and at any time all the rules fire to a degree. The
sum of all the firing rules gives the overall output.
The rule confidences are a degree of relationship
between the input fuzzy set(s) and the output fuzzy
set(s). When the rule confidence is zero, the input(s)
is not related to the output(s) so the rule does not
fire. Otherwise, the input(s) and output(s) have some
relation and the rule partially fires when the mem-
bership degree of the rule antecedent is greater than
zero. A rule can have several non-zero confidences.
When there are many rules with several non-zero con-
fidences, the network transparency is poor. Trans-
parency is a desirable feature that allows us to un-
derstand the influence of each weight (or rule con-
fidence) in the result network output. To improve
the transparency of neurofuzzy systems, the proposed
method searches for (a maximum of) two non-zero
confidences which give the same result. The effec-
tiveness of this proposed methodology is tested in a
practical control problem.
2 NEUROFUZZY STRUCTURE
A neurofuzzy system consists of various components
of a traditional fuzzy system, with the exception that
each stage is performed by a layer of hidden neurons.
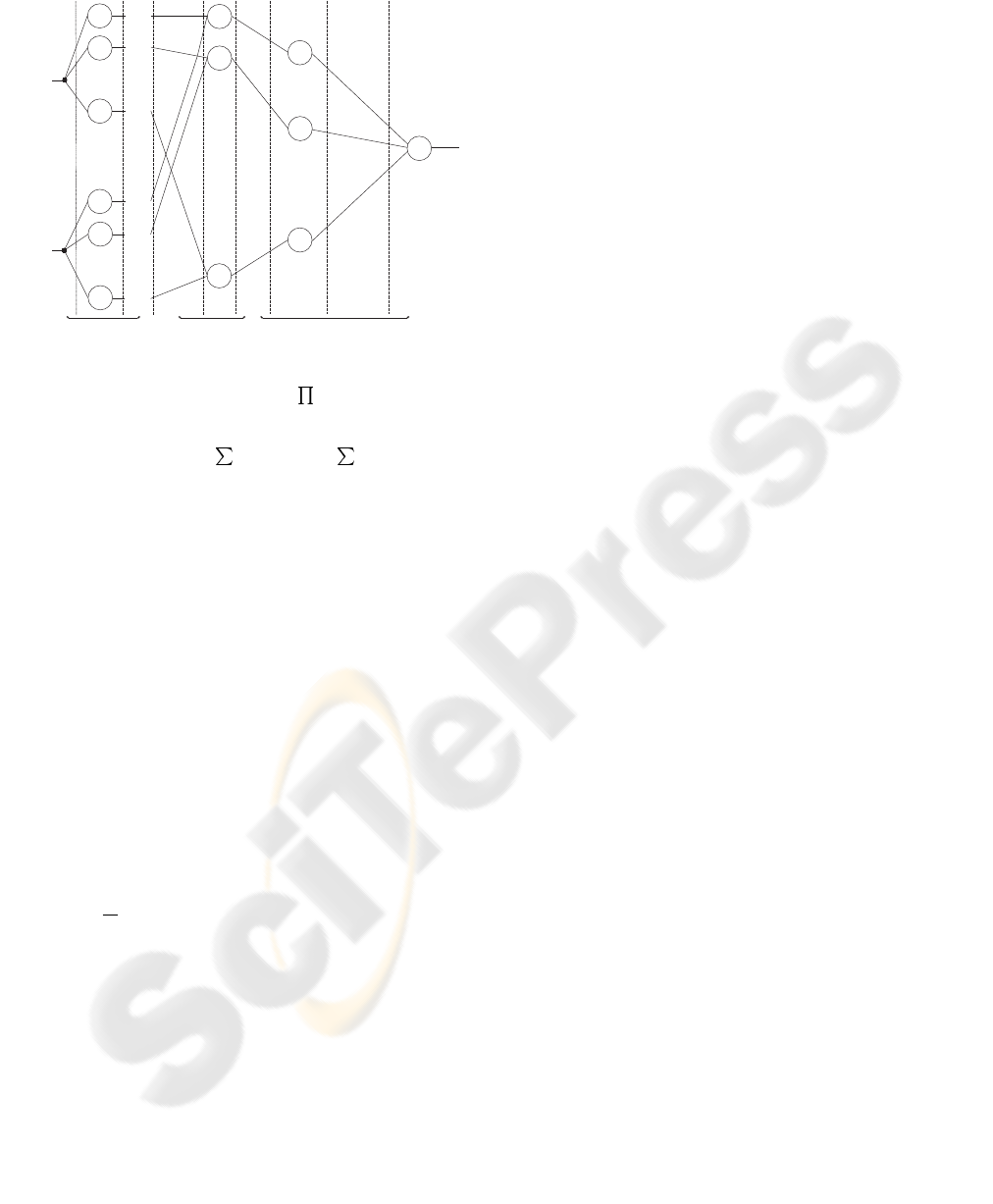
Figure 1 shows the implementation of a neurofuzzy
system. Each circle represents a neuron. These neu-
rons are fuzzy rather than McCulloch-Pitts neurons.
This means that they perform fuzzy operations (e.g.,
fuzzification, rule firing strength, defuzzification). A
fuzzy production rules relates the networks inputs,
x, to its output, y. During training, this knowledge,
which is represented as IF-THEN sentences, is stored.
A fuzzy production rule is of the form:
r
ij
: IF x is A
i
THEN y is B
j
, c
ij
297
Domínguez-López J. (2005).
METHOD TO IMPROVE THE TRANSPARENCY OF NEUROFUZZY SYSTEMS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 297-300
Copyright
c
SciTePress
.
.
.
.
.
.
Inputs
Fuzzification
layer
Fuzzyrule
layer
Weight
ofrules
Defuzzificationlayer
Output
Rules
Antecedent
(IF is )x A
.
.
.
.
.
.
.
Consequent
(THENyisB)
Antecedent
weight
Consequent
weight
Grade
11
12
1N
1
iN
i
i2
i1
m (x)
A
11
1
1
11
12
1M
w
w
w
11
22
MP
a
11
a
22
a
1R+1
a
2R+2
a
P2
a
PQ
b
11
b
12
b
1M
B
B
B
m (x)
A
12
1
m (x)
A
1N
1
A
OR
RuleP
Rule2
Rule1
m (x)
A
i1
i
m (x)
A
i2
i
i
m (x)
A
iN
i
A
A
A
A
A
Y(t)
x(t)
x(t)
1
i
Figure 1: Architecture of a typical neurofuzzy system. The
number of rules is given by P =
i
N
i
, where i is the
number of inputs and N
i
is the number of antecedent fuzzy
sets for input i while M is the number of consequent fuzzy
sets. Also we have Q =
i
N
i
and R =
i−1
k=0
N
k
.
where r
ij
is the ijth rule, A
i
represents the input
fuzzy sets, B
j
is the output fuzzy set and the rule con-
fidence is c
ij
∈ [0, 1]. The value of c
ij
indicates the
degree of confidence in the relationship between A
i
and B
j
. When c
ij
is zero the rule is inactive and does
not affect the output. Otherwise, the rule is active and
contributes to the output according to the degree of
activation of the antecedent. Subsequently, the fuzzy
rules can be learned by adapting the rule confidences,
changing the strength with which a rule fires.
Once, the neurofuzzy controller has been designed
and constructed, the objective of the selected learning
algorithm is to determine the appropriate values for
the parameters of the membership functions and the
linking weights (Chen and Peng, 1999). The weights
of the antecedent and consequent require as many pa-
rameters as modifiable parameters of the membership
functions. So, it is common that instead of a weight
vector,
w, it is a weight matrix, w . For instance,
the triangular membership functions have three para-
meters that can be updated. This leads to have sev-
eral free parameters to update, slowing the learning
process. In addition, the resulted membership distrib-
ution may not be as transparent as with the designer’s
distribution. For example, in (Berenji and Khed-
kar, 1992), before learning, the membership ‘posi-
tive small’ is in the positive region of the universe
of discourse but, after learning, it is in the negative
region, losing its meaning. This can be corrected
if the system is able to correct inappropriate defini-
tions of the labels. When the neurofuzzy system has
only one modifiable weight vector (i.e., the rule confi-
dence vector), leaving the other vectors and the fuzzy
memberships fixed, the system can still describe com-
pletely the input-output mapping for a The use of
rule confidences rather than a weight vector allows
the model to be represented as a set of transparent
fuzzy rules (Brown and Harris, 1994). However, us-
ing a rule weight vector reduces considerable the stor-
age requirements and the computational cost (Harris
et al., 2002, p. 92). Nevertheless, it is possible to al-
ternate between the rule weight vector and the rule
confidence without losing any information.
The transformation from the weight vector, w
i
, to
the vector of rule confidence, c
i
, is a one-to-many
mapping. The weight vector can be converted into
confidences by measuring its grade of membership to
the various fuzzy output sets, µ
B
j
(·):
c
ij
= µ
B
j
(w
i
)
The inverse transformation, from c
i
to w
i
, is given by:
w
i
=
X
j
c
ij
y
c
j
where y
c
j
is the centre of the jth output set µ
B
j
(u)
which has bounded and symmetric membership func-
tions.
The maximum number of rule confidences, p
c
, de-
pends on the number of inputs, n, and the number of
fuzzy sets in each input, p
i
, and in the output, q:
p
c
= q
n
Y
i=1
p
i
(1)
Accordingly, if the number of rules is large be-
cause there are many inputs and/or many fuzzy sets
per input, transparency can get lost. Consequently,
it is important to keep relatively low the number of
rules, avoiding redundant ones. In addition, as the in-
put dimension increases, the requirement of resources
(data, memory, processing time, ...) increases ex-
ponentially (Bossley, 1997). Therefore, fuzzy sys-
tems suffer from the curse of dimensionality (Bell-
man, 1961). Consequently, practical fuzzy and neu-
rofuzzy systems are reduced to problems with input
dimension typically less than four. However, if some
form of model complexity reduction is applied, fuzzy
and neurofuzzy systems can be used to solve high di-
mensional problems (Harris et al., 2002) and still be
transparent.
3 FUZZY INFERENCE ENGINE
The fuzzy inference engine evaluates the control rules
stored in the rule-base. It performs four main tasks:
rule firing, strength calculation, fuzzy implication
and rule aggregation. The current fuzzy input set is

matched with the antecedent of all rule to produces
the fuzzy output set. Then, the activated output fuzzy
sets are defuzzified to obtain the control action. The
output represents the degree of relationship between
the input and each output fuzzy set (Harris et al.,
2002). The degree of relationship between the system
inputs x and the system output y is given by:
µ
r
ij
(x, y) = µ
A
i
(x)
ˆ
∗c
ij
ˆ
∗µ
B
i
(y)
where
ˆ
∗ represents T-norm operation (e.g., min and
algebraic product functions), µ
B
i
(y) is the fuzzy out-
put set and the fuzzy input set is µ
A
i
(x), which is
obtained from the fuzzy intersection (AND) of n-
univariate fuzzy sets:
µ
A
i
(x) = µ
A
i
1
(x
1
)
ˆ
∗ · · ·
ˆ
∗µ
A
i
n
(x
n
)
In order to form a fuzzy rule R, all the individual
relations of input-output sets, µ
r
ij
, have to be con-
nected using a multivariable S-norm operator,
c
P
:
µ
R
(x, y) =
[
X
i, j
µ
r
ij
(x, y)
To produce a single fuzzy output set, µ
B
(y), the
fuzzy inference machine matches the current inputs
with the antecedents of all rules. This inference is
given by:
µ
B
(y) =
d
X
x
(µ
A
i
(x)
ˆ
∗µ
R
(x, y)) (2)
Finally, this single fuzzy output has to be converted
back into a real-value output. This is done perform-
ing a defuzzification operation. The most widely used
method is the centre of gravity (CoG) because it con-
sistently produces better results than the other meth-
ods (Bossley, 1997). The output of a fuzzy system
that uses CoG defuzzification method is given by:
y(x) =
R
Y
µ
B
(y)y dy
R
Y
µ
B
(y) dy
(3)
Using Equation 2 in Equation 3, the real-valued
output becomes:
y(x) =
R
Y
R
X
µ
A
(x)
ˆ
∗
c
P
ij
µ
r
ij
(x, y) y dxdy
R
Y
R
X
µ
A
(x)
ˆ
∗
c
P
ij
µ
r
ij
(x, y) dxdy
(4)
When the fuzzy output sets are bounded and sym-
metric, the i
th
rule confidence vector c
i
is normalised
(i.e.,
P
j
c
i
= 1), and the fuzzy inputs sets form a
partition of unity, Equation 4 reduces to:
y(x) =
R
X
µ
A
(x)
ˆ
∗
c
P
i
µ
A
i
(x)
ˆ
∗
c
P
j
c
ij
y
c
j
dx
R
X
µ
A
(x) dx
(5)
XCoG
XCoG
Figure 2: Two non-zero rule confidences can represent three
or more non-zero rule confidences.
Accordingly, the prosed method searches a c
′
ij
that
satisfies:
d
X
j
c
ij
y
c
j
=
d
X
j
c
′
ij
y
c
j
where c
′
j
has only two non-zero values and c
j
has
three or more non-zero values.
In order to find c
′
j
, the method searches for two
non-zero rule confidences that have the same centre
of gravity as the original c
j
. So, both rule confi-
dences have identical contribution in the obtention of
the real-valued output. This is illustrated in Figure 2,
where two non-zero rule confidences represent three.
4 EXPERIMENTAL EXAMPLE:
THE CART-POLE BALANCING
PROBLEM
To illustrate the proposed method and to show its ef-
fectiveness, the neurofuzzy system described in Sec-
tion 2 is used in a very popular problem to test con-
trollers: the cart-pole balancing problem. The con-
troller has to apply a sequence of right and left forces
to the cart such the pole remains balanced. The con-
troller fails if either the pole falls or the cart hits the
track end. The implemented neurofuzzy controller
has two inputs, the pole angle and pole angular ve-
locity, and one output, the applied force. The linguis-
tic variables used for the term sets are simply value
magnitude components: Negative Large (NL), Neg-
ative Medium (NM), Negative Small (NS), Zero (Z),
Small (S), Medium (M) and Large (L) for the fuzzy
sets pole angle and applied force, while for the fuzzy
set pole angular velocity they are NL, NS, Z, S and
L. The neurofuzzy controller was trained with re-
inforcement learning, using the training framework
described in (Dom
´
ınguez-L
´
opez et al., 2004). Af-
ter training, the total number of non-zero rule con-
fidences was 92. Then, the proposed method is used
to improve the transparency. The method gives a total
of 65 non-zero rule confidences. This final model is

Table 1: Rule-base and rule confidences (in brackets) obtained after applying the proposed method. There are 65 non-zero
rule confidences.
Pole angular velocity
Applied force NL NS Z S L
NL L (0.9) L (0.7) L (0.6) L (0.3) L (0.2)
M (0.1) M (0.3) M (0.4) M (0.7) M (0.8)
NM L (0.8) L (0.7) L (0.2) M (1.0) L (0.3)
M (0.2) M (0.3) M (0.8) M (0.7)
NS M (1.0) M (0.8) M (0.3) S (0.2) S (0.1)
S (0.3) S (0.7) Z (0.8) Z (0.9)
Pole Z S (1.0) M (0.2) S (0.3) Z (0.3) Z (0.2)
angle S (0.8) Z (0.7) NS (0.7) NS (0.8)
S Z (1.0) Z (0.8) Z (0.3) NM (0.7) NS (0.2)
NS (0.2) NS (0.7) NL (0.3) NM (0.8)
M Z (0.2) NM (0.7) NM (0.8) NM (0.3) NM (0.1)
NS (0.8) NL (0.3) NL (0.2) NL (0.7) NL (0.9)
L NM (1.0) NM (0.7) NM (0.4) NM (0.3) NM (0.1)
NL (0.3) NL (0.6) NL (0.7) NL (0.9)
shown in Table 1. This is a reduction of around 40%
in the number of rule confidences. So, the proposed
method has improved the transparency. Although
not shown explicitly here, the performance of both
rule-bases was identical: Both rule-bases were tested
30 times with no failure in each run of 10 min.
5 CONCLUSION
One of the major advantages of neurofuzzy systems is
their transparency, so even a non-specialist in control
can understand and manipulate the rule-base. How-
ever, the interpretability of the final model can be lost
if after training each rule has a large number of non-
zero confidences. Nevertheless, the transparency can
be recovered without affecting the system complex-
ity and performance. To improved the transparency,
the proposed methodology searched for a maximum
of two non-zero confidences per rule. These two non-
zero confidences have the same contribution as the
original ones, thus the system performance is not af-
fected. In the illustrative example, the transparency
was improved, with a reduction of 40% in the num-
ber of non-zero rule confidences. The improvement
depends on the transparency level of the original rule-
base. When the original transparency level is good,
the improvement will be low, and if the level is poor,
the improvement will be high. Using Equation 1
we can obtain the maximum and minimum improve-
ments: p
c
(q = 1)/p
c
and p
c
(q = 2)/p
c
, respectively.
Notice that here q is used as number of non-zero rule
confidences per rule rather than number of fuzzy sets
in the output.
Finally, the method described here does not rem-
edy the curse of dimensionally. It only heals the
redundancy in the rule confidences. Thus, the pro-
posed methodology should be used in conjunction
with some form of model complexity reduction (e.g.,
parsimonious modelling) in order to solve high di-
mensional problems. In this way, it is possible to
guarantee that the final model would have the best ac-
curacy and transparency trade-off.
REFERENCES
Bellman, R. (1961). Adaptive Control Processes: A Guided
Tour. Princeton University Press, Princeton, NJ.
Berenji, H. and Khedkar, P. (1992). Learning and tuning
fuzzy logic controllers through reinforcements. IEEE
Transactions on Neural Networks, 3(5):724–740.
Bossley, K. M. (1997). Neurofuzzy Modelling Approaches
in System Identification. PhD thesis, University of
Southampton, Southampton, UK.
Brown, M. and Harris, C. J. (1994). Neurofuzzy Adaptive
Modelling and Control. Prentice Hall International,
New York, NY.
Chen, C. T. and Peng, S. T. (1999). Intelligent process con-
trol using neural fuzzy techniques. Journal of Process
Control, 9(6):493–503.
Dom
´
ınguez-L
´
opez, J. A., Damper, R. I., Crowder, R. M.,
and Harris, C. J. (2004). Adaptive neurofuzzy con-
trol of a robotic gripper with on-line machine learning.
Robotics and Autonomous Systems, 48(2-3):93–110.
Harris, C. J., Hong, X., and Gan, Q. (2002). Adaptive Mod-
elling, Estimation and Fusion from Data: A Neuro-
fuzzy Approach. Springer-Verlag, Berlin and Heidel-
berg, Germany.
