IDENTIFICATION OF A CAR-LIKE VEHICLE via MODULATING

FUNCTIONS

Davide Corsanini

Department of Electrical Systems and Automation, University of Pisa

Via Diotisalvi 2, 56126 Pisa, Italy

Fabrizio Tocchini

Department of Electrical Systems and Automation, University of Pisa

Via Diotisalvi 2, 56126 Pisa, Italy

Keywords:

Modulating functions, uncertain systems modelling, car-like vehicle, online identiﬁcation.

Abstract:

This paper describes an interesting application of the modulating functions technique to model identiﬁcation

of a car-like vehicle that has to face various types of surface. Several models have been obtained in different

operating conditions. The construction of a ‘mean model’ will make possible the design of a robust control

for unmanned guidance purposes. An alternative control strategy based on adaptive methods is also suggested

by means of an online implementation of the technique.

1 INTRODUCTION

In model identiﬁcation literature, the modulating

functions technique plays a very important role. Sev-

eral published works have shown excellent results as

for the characterization of linear models, see (Shin-

brot, 1957) or (Balestrino et al., 2003). Recently,

an appealing application has involved the character-

ization of various classes of nonlinear models, see

for example (Pearson, 1992). In (Balestrino et al.,

2000) a very useful adaptation of the method is pro-

vided for the identiﬁcation of systems with an un-

known delay. In general, the most frequently inves-

tigated ﬁelds are model identiﬁcation of electrical en-

gines (Daniel-Berhet and Unbehauen, 1996), switch-

ing converters (Balestrino et al., 2003) and robot com-

ponents (Daniel-Berhet and Unbehauen, 1997).

The aim of this work is the application of such

technique to model identiﬁcation of a car-like vehi-

cle, that has to face several types of surface (dry and

wet asphalt, dry and wet grass) and different operat-

ing conditions (presence or absence of a person on

board). Various linear models are then derived in the

above-mentioned conditions and a satisfying ﬁtting of

real data is consequently obtained. We are also go-

ing to provide a comparison between the estimation

errors of the original model supplied by the manufac-

turer and the model deduced from the identiﬁcation

process.

The further step will be the design of a control law

for the unmanned guidance of the vehicle. The com-

putation of a ”mean model” will allow us to set the

problem of the controller’s design in terms of robust

control problem.

Last, the possibility of an online identiﬁcation is

presented. In this way an adaptive control strategy

can be implemented.

This paper is organized as follows: in Section 2

the vehicle and the manufacturer’s model; in section

3 the modulating functions method is reviewed and

the identiﬁed models in different conditions are com-

puted; in section 4 the mean model is derived and

the control problem is formulated; in Section 5 on-

line identiﬁcation is presented and, in Section 6 some

conclusions are reported.

2 THE CAR-LIKE VEHICLE

The vehicle

has been originally conceived as a caddy

vehicle for golf courses (see Figure 1). It is a three

wheels vehicle equipped with a DC motor supplied

with two 12 volt batteries; the two back wheels are

for the traction, the wheel in the front is for the di-

rection. Our ﬁnal goal is the realization of an un-

manned guidance; for this purpose the caddy has been

equiped with a linear actuator

for the steering, and

By courtesy of Bestkart S.N.C., Pionca di Vigonza

(Padova), Italy.

By courtesy of Ognibene Elettromeccanica Srl,

Bologna, Italy.

211

Corsanini D. and Tocchini F. (2005).

IDENTIFICATION OF A CAR-LIKE VEHICLE via MODULATING FUNCTIONS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 211-217

DOI: 10.5220/0001181802110217

 SciTePress

with a couple of sensors

for the speed and position

of the wheels. We have also designed control and

data acquisition electronics interfacing the motor, the

linear actuator and the sensors. A microcontroller Mi-

crochip PIC 16F874 plays the main role. The chip has

40 PIN: 4 are for the supply, 1 is for the asynchronous

reset, 3 are for synchronous serial communication, 2

are for the asynchronous serial communication, the

remnant is for input and output data.

Figure 1: The caddy vehicle.

To realize the caddy control and the setting of the

interface card we will have to ﬁgure out an estima-

tion of the behavior of the different components that

compose the vehicle.

The caddy can be split into two independent sub-

systems:

• Driver + traction motor

• Linear actuator driver + steering

Concerning the subsystem driver + traction motor,

the manufacturer endows the caddy with an input-

output characteristic derived in no load condition (i.e.

without a passenger). To verify the coherence with

real data we have designed a program test imple-

mented on the interface card. In this test we have fur-

nished various torque steps as inputs to the driver of

the motor and we have measured the velocity with a

100 Hz sampling frequency. We have distributed in

a quite uniform way the voltage interval 0-5 Volt into

the digital range 0-255, with a little more dense ﬁtting

in proximity of the bends. As a result we have ob-

tained a fairly good approximation of the ideal char-

acteristic (see Figure 2), but this however fails if we

consider, for example, a passenger.

As regards the transfer function, the manufacturer

provides the following ﬁrst order model:

G(s) =

1.8s + 22.7

(1)

By comparing the output of this model with the

real outputs measured in different operating condi-

tions (with or without passenger) with respect to the

By courtesy of Tekel Instruments Srl, Torino, Italy

60 80 100 120 140 160 180 200 220

−1

−0.5

0.5

1.5

2.5

division (VOLT)

m/s

Speed vs Voltage

Real case

ldeal casel

Figure 2: Ideal and real input\output characteristic in no

load condition.

same inputs (random sequence of steps), it turns out

from the analysis of data that the description of the

dynamic behavior of the system is not satisfying. The

gap increases in presence of a passenger and in the

case of motion on grass (see Figures 3 and 4).

0 5 10 15 20 25

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

time (sec)

speed (m/s)

Model validation

Figure 3: Asphalt test with passenger (thin: ﬁrst order

model response, thick: real response).

In order to achieve a better description of the dy-

namics of the caddy, an identiﬁcation procedure is

needed.

3 THE MODULATING

FUNCTIONS IDENTIFICATION

By means of input-output data analysis we are look-

ing for a computation of a linear model for the caddy.

The structure of this model must be as simple as pos-

sible (i.e. with a minimum order).

The measured output signal presents a non negli-

gible noise component and there are also unwelcome

variations due to the unevennesses of the ground. For

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

212

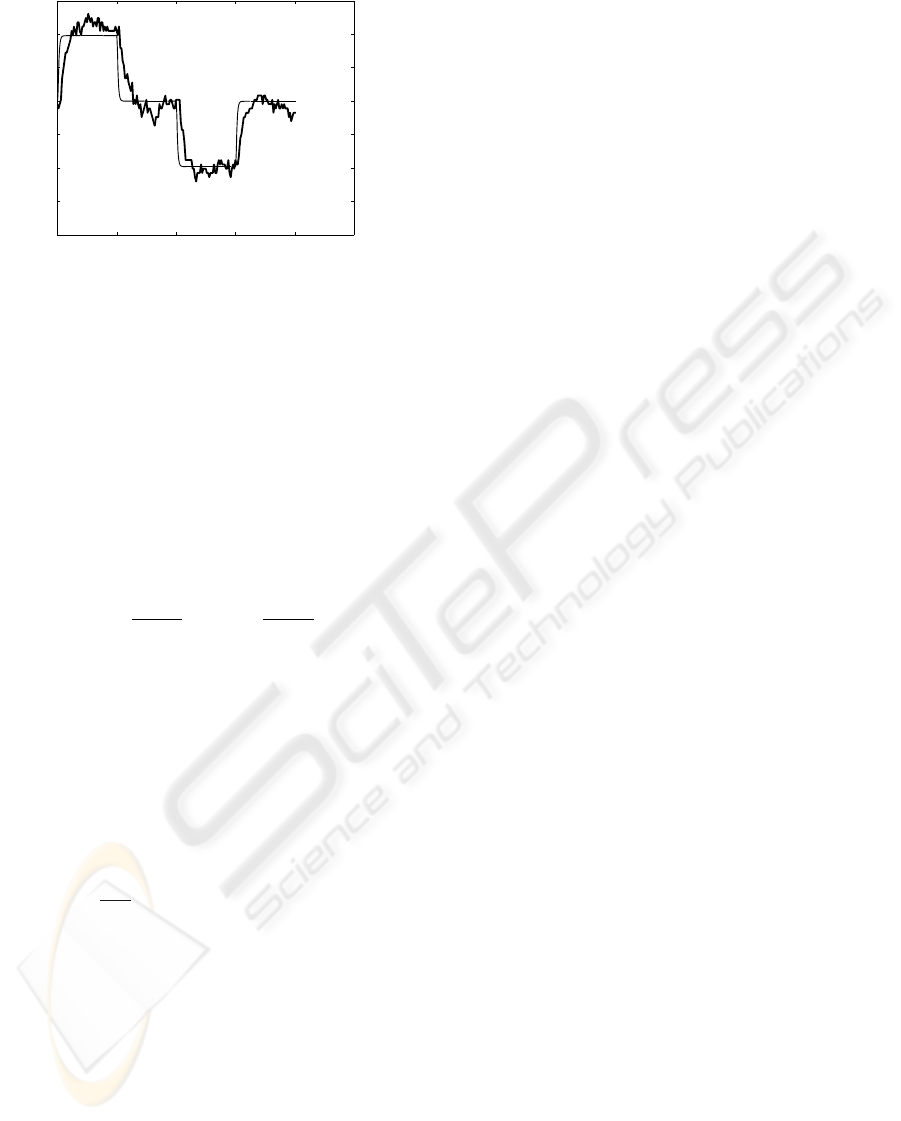
0 5 10 15 20 25

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

time (sec)

speed (m/s)

Model validation

Figure 4: Grass test without passenger (thin: ﬁrst order

model response, thick: real response)

this reason, an identiﬁcation procedure capable to ex-

tract reliable models even in these conditions is nec-

essary.

3.1 The modulating functions

Consider continuous n-th order linear processes mod-

eled by the following differential equation:

i=0

y(t)

i=0

u(t)

(2)

where u(t) is the input signal and y(t) the output one.

The coefﬁcients a

and b

are the unknows of the sys-

tem.

Now deﬁne a set of smooth functions Φ(t) having

the following properties:

Φ(t) =



Φ(t) t ∈ [0, T]

0 t 6∈ [0, T ]

(3)

∃

, ∀i = 1, . . . , p, p ≥ n (4)

(i)

(0) = Φ

(i)

(T ) = 0, i ≤ n. (5)

The time interval I = [0, T ] is commonly named

integration window. We thus denote modulating func-

tions Φ(t) function along with with its derivatives.

Multiplying both members of (2) by Φ(t) and inte-

grating over I we have:

i=0

Φ(t)y

(i)

(t)dt =

i=0

Φ(t)u

(i)

(t)dt (6)

Applying the integration by parts rule and keeping the

property 5 in mind, we get:

i=0

(−1)

(i)

(t)y(t)dt =

i=0

(−1)

(i)

(t)u(t)dt (7)

The previous statement is an algebraic equation.

The unknows are the coefﬁcients of (2) and the gen-

eral solution is:

= (−1)

(i)

(t)y(t)dt (8)

= (−1)

(i)

(t)u(t)dt (9)

Without loss of generality we assume:

= 1 (10)

Therefore, in order to determine all the unknown pa-

rameters a

and b

, at least n + m + 1 linearly in-

dependent equations are required. These equations

can be generated discretely by shifting the modulat-

ing function along the measured input-output data. In

this manner we obtain the following linear algebraic

system:

Az = c (11)

where z is the vector of unknown parameters. The

matrix A and the vector c consist of terms depending

on the coefﬁcients α

and β

A =

0,1

. . . α

m,1

−β

1,1

· · · − β

n,1

. . . . . .

0,k

. . . α

m,k

−β

1,k

· · · − β

n,k

(12)

c = [β

0,1

. . . β

0,k

]

(13)

with k ≥ n + m + 1.

If the equation’s number is greater than the number

of unknown parameters, a pseudoinverse solution can

be determined.

Summarizing, the most important features of this

technique are:

• the identiﬁcation process occurs directly in the time

domain;

• the knowledge of time derivatives of the input and

the output is not necessary;

• the integral nature of the procedure cuts the high

frequency dynamics: the bandwidth is 1/T .

Due to good ﬁltering characteristics and easiness

of implementation, the most popular class of modular

functions is the class of spline functions introduced

by Maletinsky (see (Maletinsky, 1978), (Maletinsky,

1979)). In Figure 5 we are showing some examples

of spline functions.

IDENTIFICATION OF A CAR-LIKE VEHICLE via MODULATING FUNCTIONS

213

Figure 5: Spline functions of order 6.

Set now as operating point the condition in which

the caddy receives the constant input U = U

. At the

output terminal a constant signal Y = Y

is measured.

In order to apply the modulating function algorithm

the following steps are required:

1. excitation of the system with the input U = U

+u.

The u term represents the variation with respect to

the ﬁxed operating point. The u input must excite

all the dynamics of the system;

2. storage of the corresponding output signal Y =

+ y, where y is the variation component;

3. computation of u and y from signals U and Y ;

4. selection of the system structure (number of poles

and zeros) and selection of the integration window;

5. identiﬁcation procedure applied to u and y.

An appropriate set of data is needed for derive a

number of independent equations sufﬁcient for the pa-

rameter’s calculation.

3.2 The Identiﬁcation Procedure

The likely operating conditions that we have consid-

ered are are the following:

1. Dry asphalt;

2. Dry asphalt with load (passenger);

3. Grass;

4. Grass with load.

The reference input is U

= 170 (digital scale). For

each operative condition several data-sets have been

acquired for different input signals u and a validation

data-set have been selected.

The input signal has been built with rectangular

pulses of variable amplitude. The duration of the

pulses changes along the data sets.

Different models have been obtained for each data

set and have then been compared to the validation

data-set of the corresponding operating condition. For

this purpose the measured output has been compared

to the predicted output of the model and the mean

square error has been computed.

The models have been obtained by different model

structure (number of poles and zeros) and different

amplitude of the integration window. Some examples

are shown in Table 1.

Table 1: Examples of different identiﬁcations. Only the best

models with respect to the integrator window T are listed.

Operating condition 1

Model Structure T (s) MSE (m/s)

1 pole 4 0.04

2 poles 2.5 0.02

2 poles, 1 zero 2 0.03

manufacturer - 0.12

Operating condition 2

Model Structure T (s) MSE (m/s)

1 pole 5 0.036

2 poles 3.5 0.024

2 poles, 1 zero 3.5 0.038

manufacturer - 0.122

Operating condition 3

Model Structure T (s) MSE (m/s)

1 pole 4.5 0.054

2 poles 3.5 0.048

2 poles, 1 zero 2.5 0.054

manufacturer - 0.121

Operating condition 4

Model Structure T (s) MSE (m/s)

1 pole 4 0.054

2 poles 4.5 0.049

2 poles, 1 zero 2 0.049

manufacturer - 0.119

The examples are related to the data sets showing

the features depicted in Table 2. In ﬁgures 6-9 it is

shown a comparison with real data.

In terms of mean square error, good results are ob-

tained even with simple models such as second order

transfer function with or without zero. In our case

the presence of the zero does not change signiﬁcantly

the mean square error; therefore, for the sake of sim-

plicity, we can select the second order model without

zero.

The application of the delay version of modulating

function algorithm (Balestrino et al., 2000) does not

have shown any remarkable delay.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

214

10 15 20 25 30 35

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

Operating condition 1

time (s)

v (m/s)

Real Data

Identified Model

Manufacturer Model

Figure 6: Operating Condition 1.

0 2 4 6 8 10 12 14 16 18 20

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

Operating condition 2

time (s)

v (m/s)

Real Data

Identified Model

Manufacturer Model

Figure 7: Operating Condition 2.

4 BASIS FOR ROBUST CONTROL

Thanks to previous analysis, we currently own a set of

maps describing the behavior of the vehicle in differ-

ent conditions. The basic idea is the construction of a

mean model, that, for our purposes, plays the role of

nominal plant. For this aim a very simple approach is

followed: a mean model is derived for every operating

condition and after the ﬁnal mean model is computed

as a mean of these results:

j=1

test

i=1

test

(14)

where N

is the number of operating conditions (dry

asphalt with or without a person on board, dry grass

with or without a person on board, etc.), N

test

is the

number of models derived in different tests in a given

operating condition.

The term ”uncertainty” refers to the differences or

errors between models and reality. For this reason

5 10 15 20 25 30 35

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

Operating condition 3

time (s)

v (m/s)

Real Data

Identified Model

Manufacturer Model

Figure 8: Operating Condition 3.

5 10 15 20 25 30

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

Operating condition 4

time (s)

v (m/s)

Real Data

Identified Model

Manufacturer Model

Figure 9: Operating Condition 4.

we are deﬁning uncertainties the deviations with re-

spect to the mean model (14) of all models computed.

The structured representation of uncertainty in the so-

called multiplicative form is (Zhou and Doyle, 1998):

∆

= (I + W

(s)∆

(s))P

(s) (15)

where W

(s) is a stable transfer matrix describing

the spatial and frequency structure of uncertainty. In

this manner P

∆

is conﬁned in a normalized neighbor-

hood of the nominal plant P

(s). For every model

derived in Section 2 the multiplicative uncertainty is

deﬁned as:

∆

(s) =

(s) − G

(s)

(16)

We then look for a weight transfer function W

such

that:

(jω)| ≥ |∆

(jω)|

In our case the function W

(s) is also proper since

(s) and G

(s) have the same relative degrees. Ap-

plying this procedure to the data set, we can ﬁnd the

IDENTIFICATION OF A CAR-LIKE VEHICLE via MODULATING FUNCTIONS

215

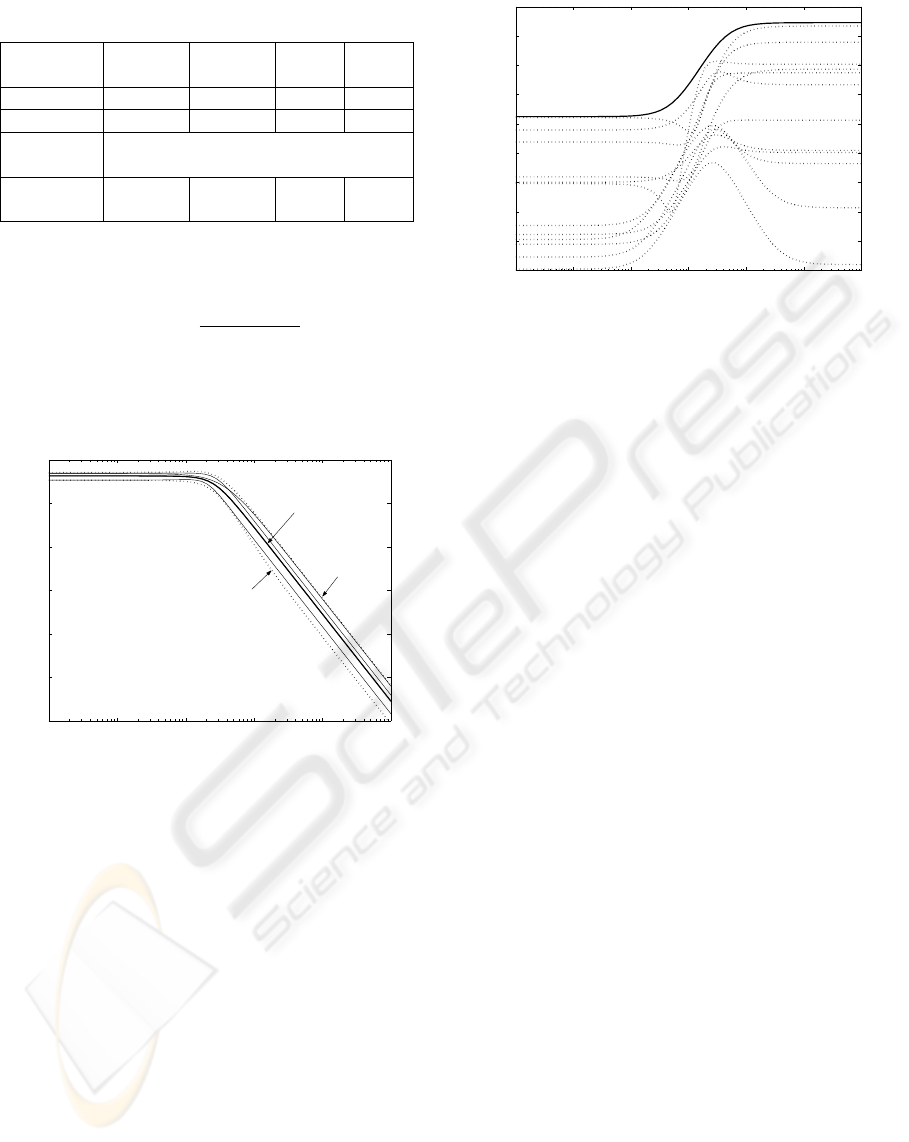
Table 2: Data set features.

Operating

Mode

1 2 3 4

surface Asphalt Asphalt Grass Grass

Passenger No Yes No Yes

Min/Max

step

-10/+10

Step du-

ration (s)

1.5 1.5 2 2

following result:

(s) =

1.3(s + 0.6)

(s + 3.8)

In Figure 10 the bounded region including all the

models is shown, whereas in Figure 11 the frequency

response of the W

(jω) and ∆

(jω) is reported.

−2

−1

−140

−120

−100

−80

−60

−40

−20

Frequency (rad/sec)

Magnitude (dB)

Nominal Model

Lower Bound

Upper Bound

Figure 10: Bounding region of P

∆

= [1 +

(s)∆(s)]P

(s)

5 ONLINE IDENTIFICATION

The ofﬂine version of the modulating function tech-

nique has been used to estimate uncertainties with re-

spect to the chosen nominal model. In order to obtain

a likely uncertain model several tests are necessary.

An online version of this technique can be easily

implemented (Balestrino et al., 2004). In this way an

alternative approach for the control design, based on

adaptive method, seems to be possible. The design of

the controller will require an analysis of the conver-

gence of the method.

To perform the online version of modulating func-

tions algorithm we will have to choose:

• The model structure;

• The number of rows of the A matrix deﬁned in 12;

−3

−2

−1

−40

−35

−30

−25

−20

−15

−10

−5

Frequency (rad/sec)

Magnitude (dB)

Figure 11: ∆

(dashed lines) and the bound

(solid line).

• The integration window duration(T);

• An initial estimation of z (given, for example, by a

ofﬂine procedure);

Input-output data are stored continuously. Every T

seconds a new equation is generated using (7) and the

following steps are performed (see Figure 12):

1. Starting from the previous matrix A

k−1

and the

vector c

k−1

, the A

matrix and the vector c

are

updated with a First In First Out strategy taking in

account the new equation;

2. The following index is calculated:

∆ = kA

k−1

− c

k (17)

were z

k−1

is the previous parameter’s vector;

3. If ∆ > ǫ, where ǫ is a ﬁxed positive threshold,

then the new row brings meaningful new informa-

tion and the algorithm can proceed to the next step.

Otherwise, the A

k−1

and c

k−1

are restored and the

algorithm returns to step 1;

4. computation of the new z

. Return to step 1.

It is worth to notice that, in order to increase the

frequency of the parameter’s computation, the inte-

gration windows can overlap. In Figure 13 we are

showing the application of the online algorithm in dry

asphalt operating mode.

6 CONCLUSION

The modulating functions technique guarantees the

identiﬁcation of a second order linear model, which

thoroughly describes the dynamics of a caddy vehicle.

The ofﬂine classic version of the procedure allows to

set the control problem for unmanned guidance from

the point of view of robustness. The online version

of the technique enables an adaptive control strategy.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

216

Caddy

Modulation

Matrix

Update

Data Check:

useful information ?

Update

Model

hold

Yes

Figure 12: Block diagram of online algorithm.

15 20 25 30 35

0.2

0.4

0.6

0.8

15 20 25 30 35

0.05

0.1

0.15

0.2

15 20 25 30 35

0.02

0.04

0.06

time (s)

Figure 13: Second order model in dry asphalt: Ofﬂine pa-

rameters (dashed line), Online parameters (solid line).

Our intent in a near future is the design and the im-

plementation of controllers following the guidelines

showed in this work.

ACKNOWLEDGEMENT

The authors would like to express their sincere appre-

ciations to Roberto Mati, Manuele Cellini and Luca

Greco for their technical support and their gratitude

to Prof. Aldo Balestrino for his advices.

REFERENCES

Balestrino, A., Bolognesi, P., Landi, A., and Sani, L. (2004).

Fault detection of pm synchronous motor via modu-

lating functions. In Symposium on Power Electronics,

Electrical Drives, Automation & Motion, SPEEDAM.

Balestrino, A., Landi, A., and Sani, L. (2000). Para-

meter identiﬁcation of continuous systems with mul-

tiple input time delays via modulating functions.

IEE Proceedings on Control Theory & Applications,

147(1):19–27.

Balestrino, A., Landi, A., and Sani, L. (2003). Large sig-

nal models of zvs class E

resonant converters. In

10th European Conference on Power Electronics and

Applications.

Daniel-Berhet, S. and Unbehauen, H. (1996). Application

of the hartley modulating functions method for the

identiﬁcation of the bilinear dynamics of a dc motor.

In 35th Conference on Decision and Control.

Daniel-Berhet, S. and Unbehauen, H. (1997). Physical para-

meter estimation of the nonlinear dynamics of a single

link robotic manipulator with ﬂexible joint using the

hmf-method. In Proceedings of the American Control

Conference.

Maletinsky, V. (1978). Identiﬁcation kontinuierlicher dy-

namischer prozesse. PhD thesis, ETH Zurich.

Maletinsky, V. (1979). Identiﬁcation of continuous dy-

namical system with spline-type modulating function

method. In IFAC Congr. On Parameter Identiﬁcation

and Parameter Estimation.

Pearson, A. E. (1992). Explicit parameter identiﬁcation for

a class of nonlinear input/output differential operator

models. In 31st Conference On Decision And Control.

Shinbrot, M. (1957). On the analysis of linear and non linear

systems. Trans. ASME, 79:547–552.

Zhou, K. and Doyle, J. C. (1998). Essentials of robust con-

trol. Prentice Hall.

IDENTIFICATION OF A CAR-LIKE VEHICLE via MODULATING FUNCTIONS

217