IMPROVEMENT ON THE POLE-PLACEMENT CONTROL

SCHEME BY USING GENERALIZED SAMPLED-DATA HOLD

FUNCTIONS

David J. Donaire, Rafael Bárcena, Koldo Basterretxea

Department of Electronics and Telecommunications, University of the Basque Country, La casilla 3, Bilbao, Spain

Keywords: sampled-data systems; GSHF; pole-placement control.

Abstract: This paper studies the benefits the use of GSHF can afford to the pole-placement control scheme. The

GSHF

makes possible to locate the zeros of the discretized plant arbitrarily in the Z plane. This property can

be taken advantage of to improve the performance of the pole-placement control. In this article a new design

method is suggested and a simulations-based application example is carried out. In the application example

the improvements this method involves with respect to the classical design method are noticed.

1 INTRODUCTION

Usually, most sampled data control systems use the

Zero Order Hold (ZOH). However, some authors

((Kabamba, 1987) (Bai and Dasgupta, 1990) (Er and

Anderson, 1994) (Yan et al., 1994) (Rossi and

Miller, 1999) (Barcena abd De la Sen, 2003)) have

proved that using hold patterns which differ from the

zero order extrapolation, that the ZOH carries out,

can improve the discrete performance of the hybrid

system.

The GSHF (Generalized Sampled-data Hold

nction), device which has been widely studied

(Kabamba, 1987) (Bai and Dasgupta, 1990) (Er and

Anderson, 1994) (Yan et al., 1994), has a generic

hold function which can be tuned to obtain some

advantages. For example, (Kabamba, 1987) proves

that the zeros of the discretized plant can be placed

arbitrary in the Z plane by tuning the hold function

of the GSHF.

Several hybrid control schemes are based on the

cancellation

of the zeros of the discretized plant with

the controller poles. The pole-zero cancellation

cannot be done if there is any unstable zero in the

discretized plant, because it would make the system

internally unstable (Jury, 1956). This cancellation

would not be advisable either if there is any

insufficiently damped zero, since the cancellation of

this zero could cause intersample ripple (Clarke,

1984). It is always possible, by using the GSHF, to

stabilize the zeros of the discretized plant, when are

unstable, or to increase the stability degree of the

critically damped ones, in order to make possible a

safe cancellation. Therefore, this device makes

possible the use of mentioned control schemes.

On the other hand, it is well known (Kuo, 1992) that

e relative location of the zeros from the poles

influences in the system response. Therefore, the

GSHF can be used to place the zeros of the

discretized plant in more favourable locations from

the viewpoint of the control strategy and, in that

way, to improve the performance achieved with the

ZOH.

Although the mentioned advantages, both

conce

rning the discrete performance of the hybrid

system, some authors ((Feuer and Goodwin, 1994)

(Freudenberg et al., 1995) (Freudenberg et al.,

1997)) have proved that the use of the GSHF can

cause intersample difficulties which do no appear

when the ZOH is used. Nevertheless, this happens in

designs in which the intersample ripple these devices

can cause has not been taken into account. However,

when this possibility is taken into account by the

design method, it is possible to get somewhat degree

of improvement in the discrete performance of the

hybrid systems, without incurring in a too large

deterioration of the intersample performance. An

example of this appears in (Hjalmarsson and

Braslavsky, 1999).

Using the GSHF carries another adverse

effect: its

static hold function requires that the control signal

varies even during the steady-state. This can cause

the actuator fatigue and accelerate its wear. In (Chan,

2002) it is suggested an alternative to the static hold

pattern of the GSHF. The device suggested in that

J. Donaire D., Bárcena R. and Basterretxea K. (2005).

IMPROVEMENT ON THE POLE-PLACEMENT CONTROL SCHEME BY USING GENERALIZED SAMPLED-DATA HOLD FUNCTIONS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 92-98

DOI: 10.5220/0001181900920098

 SciTePress

paper converges asymptotically toward a ZOH input

pattern as the controlled system response tends to the

steady-state step response. This eliminates the

unceasing magnitude changes and the ripple the

control signal suffers during the steady-state step

response when the GSHF is employed. The analysis

of this device, variable GSHF from now on, and the

benefits its use can afford to the pole-placement

control will be the objectives of this paper.

This paper is organized in the following manner. In

section 2 the most important characteristics of the

variable GSHF are described and the pole-placement

control scheme structure is commented. In the

section 3 a new design method for this controller is

suggested. This design methodology takes into

account the variable GSHF properties so that the

benefits that this hold device can afford are taken

advantage of. In this way the pole-placement control

scheme performance is improved. In section 4 a

simulations-based application example is carried out

and the outcomes are compared with the obtained

ones by the classical design method. To finish, the

conclusions are drawn in the section 5.

2 PRELIMINARIES

2.1 Variable GSHF (Chan, 2002)

The variable GSHF contains m discrete filters which

process the incoming discrete signal with the sample

time T

. A MISO discrete filter of m inputs which

works with a sampling time of T

/m processes the

output signals of these m filters. The output signal of

this filter is rebuilt with a ZOH which works at the

same sampling rate. The Fig. 1 shows the structure of

the variable GSHF.

The variable GSHF divides the sampling time T

m subintervals and in each one of these subintervals

the hold function is kept constant. The amplitude

associated to each one subinterval depends on the

state of the MISO filter variable GSHF contains.

Therefore, the gains of each one subinterval may

vary from a sampling time to another. For that reason

we call it variable GSHF.

Using a variable GSHF with m=2 and a suitable

selection of the parameters of the discrete filters it is

possible to locate the zeros of any strictly proper

transfer function of arbitrary order which no contains

zeros, arbitrarily in the Z plane (Chan, 2002) (Chan,

1998). This is the case that we will study in this

paper.

The v

(z),...,v

(z)

filters are introduced to produce the

redundancy in the discrete control signal necessary

for zero placement. These filters are defined by (1)

where c

(z) and d(z) are polynomial of the same

degree. The MISO filter is defined by equation

system (2) where s

, with l=1,2,...,m, and p are

scalars.

()

() () , 1,2,...,

()

vz rz l m

(1)

() ()

() () ()

(0) 0

wk pwk svk

uk wk v k

⎧

⎛⎞

+= +

⎪

⎜⎟

⎝⎠

⎪

⎨

⎪

⎩

∑

(2)

Figure 1: Variable GSHF

If the process to be controlled, discretized by the

ZOH contained in the GSHF, has the following

discrete-time

(1) () ()

() ()

kAxkBu

yk Cxk

+= +

⎧

⎨

⎩

(3)

then, the state space representation of the system

composed of MISO filter and the discrete system

represented by (3) has the discrete time

representation described by the system (4).

(1) () ()

() ( 0)()

zk Fzk Gv k

yk C zk

⎧

+= +

⎪

⎨

⎪

⎩

∑

(4)

where

()

⎛

⎜

⎝⎠

⎞

⎟

]

∈

(5)

⎛⎞

⎜

⎝⎠

(6)

[

, 1,...,

−

⎛⎞

⎜⎟

⎝⎠

∑

(7)

In the equation system (2) it is noticed that, when the

MISO settles, the signal which is reconstructed by

IMPROVEMENT ON THE POLE-PLACEMENT CONTROL SCHEME BY USING GENERALIZED SAMPLED-DATA

HOLD FUNCTIONS

the ZOH at each multiple of T

/m begin to update

only a time per sampling period. Therefore, the

variable GSHF behaves as a GSHF during transient

response and as a ZOH in the steady state. This

eliminates the unceasing changes of magnitude and

achieves to reduce the ripple that the static hold

pattern of the GSHF produces.

Using two subintervals (m=2), the assignment of the

discrete transfer function numerator is obtained

resolving the following diophantine equation:

11 2 2

() () () () () () ()

zc z g zc z g zc z numz

=+ =

∑

(8)

where c

(z) are the numerator polynomial of the m

discrete filters which precede the MISO filter, num(z)

is the polynomial required as numerator of the

discretized plant transfer function and g

(z) is the

polynomial of the numerator of each one of the m

discrete systems obtained when the equation system

(4) is particularized to a concrete value of l.

It is important to point out that the implementation of

the variable GSHF involves no additional hardware

since the discrete filters are implemented in the

computer and, therefore, the only hardware needed to

implement this device is a ZOH.

2.2 Control scheme

In this paper the improvement the use of GSHF can

contribute to the pole-placement discrete control,

which is vastly studied in (Aström and Wittenmark,

1990), is analyzed.

In this control scheme, which structure is represented

in Fig. 2, the polynomial R(z), S(z) and T(z) of the

discrete filters of the feedback loop and

precompensator are calculated to match the

behaviour of the closed-loop with the reference

model. This is carried out by solving the following

equations

() () () ()

() () ()() () ()

TzBz B zA z

zRz BzSz A zA z

(9)

where A

(z) is a polynomial introduced to ensure the

solvability of the second equation of (9). The

discretized plant zeros are transmitted to the

reference model unless they are cancelled with the

controller poles. It is important to point out that only

stable zeros can be cancelled. For this reason the B(z)

polynomial is factorized into the following

polynomials: B

(z) and B

(z). Where B

contains the

stable zeros of the discretized plant the designer

wants to cancel and B

(z) contains the unstable zeros

and the stable zeros the designer decides to transmit

to the reference model. The zeros of the B

(z) are

necessarily roots of the numerator of the reference

model and, therefore, when B

(z) contains any zero,

the reference model cannot be chosen totally freely.

For this reason the polynomial B

(z) is factorized in

the following way

() () ' ()

Bz BzB z

−

(10)

where B’

(z) is the polynomial contained in B

that

can be chosen freely. In other respect, the polynomial

(z) is cancelled with the controller poles and

therefore the roots of B

(z) must be roots of the

polynomial R(z)

Figure 2: Reference model control scheme

() '()RBzRz

(11)

Using (10) and (11) in (9) the equations obtained are

() ' () ()

() '() ()() () ()

Tz B zA z

zR z B zSz A zA z

−

(12)

By solving the equations (12) the discretized plant

behaviour is matched with the reference model

described by the equation (13).

'() () () ()

()

() ()

()

BzBzAzBz

Az Az

−+

(13)

3 DESIGN METHOD

This paper accomplishes the analysis of the

improvements that the GSHF can contribute to pole

placement control scheme. In this control scheme, the

first step is to locate the poles of the reference model

in terms of the required behaviour. Then, two

possibilities exist. It is possible to cancel the zeros

with controller poles or to transmit them to the

reference model. Is well known (Kuo, 1992) that the

relative position of the zeros from the poles

influences on the closed loop performance. In a

generic manner, to be able to relocate the zeros of the

closed loop anywhere in the Z plane supposes an

advantage. However, it is not always possible, since,

if the zeros of the plant are unstable or not

sufficiently damped, it is not advisable to cancel

them. Therefore, when the ZOH is the device used

for the reconstruction and the discrete transfer

function has this kind of zeros, we are forced to

transmit them to the reference model.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

The variable GSHF, however, allows us to relocate

the zeros arbitrarily in the Z plane. Therefore, this

device permits to avoid these problems. Besides, two

possibilities exist.

The first method lies in using the variable GSHF to

locate the zero of the discretized transfer function of

the plant in the position where the reference model

has its zero. This allows achieving the model

matching without carrying out a cancellation.

The second way to match the closed-loop discrete

behaviour with the reference model using the GSHF

lies in positioning the zero of the discretized plant

transfer function in a place where the discrete zeros

are suitable to be cancelled without incurring in

intersample ripple. If the zero is located in a place

with this characteristic, then it is possible to cancel

this with the controller and to place the zero of the

system in the prescribed position.

4 APPLICATION EXAMPLE

In this section it is carried out a comparative study

between the performance attained in pole-placement

scheme by the ZOH and the attained one by a

variable GSHF, tuned as is described in section 3.

Both methods are applied for accurate positioning of

a computer hard disk read/write head. The model of

the read/write head used (Franklin et al., 1992) is

described by de following differential equation

() () () ()

It Ct Kt Kit

θθθ

++ =

 

(14)

where

is the inertia of the head assembly, C is the

viscous damping coefficient of the bearings, K is the

return spring constant, K

, is the motor torque

constant, i(t) is the input current and

(t) is the

angular position of the head. With the parameters

suggested in (Franklin et al., 1992) (I=0.01 Kgm

C=0.004 Nm/rad, K=10Nm/rad y K

=0.005Nm/A)

the transfer function that describes the dynamic of

the plant is

()

0.4 1000

(15)

To discretize a process, a usual agreement suggests

choosing the sampling time 20 times higher than the

continuous plant bandwidth (Kuo, 1992). To

accomplish with this agreement the sampling time is

fixed to 0.006 s. Pole-placement controller is the

scheme used in this section. The discrete behaviour

that is wished to transmit to the plant is described by

the following transfer function:

(

)

0.30417 0.4

()

1.2 0.3825

−

−+

(16)

When the control objective is reached, the equivalent

damping coefficient of the closed-loop system is

about 0.89. This reference model has been chosen to

obtain the closed-loop system with the minimal

settling time. This selection is carried out due to the

fact that the settling time is one of the more

important specifications that the step response of a

hard disk needs to improve since the read/write

operation cannot start until the read/write head of the

hard disk places correctly in the position the

reference signal requires.

However, if the ZOH is used the obtained discrete

transfer function is

(

)

8.9659 10 0.9992

()

1.962 0.9976

ZOH

−

⋅+

−+

(17)

This transfer function has its zero located almost on

the unit circle and it is not advisable to cancel this by

the controller. Fig. 3 shows the obtained result when

necessary cancellation to catch up with the discrete

reference model is carried out.

Figure 3: Unit-step response of the compensated system

by using ZOH device when discrete controller cancels the

discretization zero

Hence, it is necessary to transmit the zero of the

process to the reference model. When the zero is

transmitted to the reference model the system has the

step response shown in Fig. 4.

However, using GSHF it is possible to move the zero

from the place that it presents when ZOH is used. On

the one hand it is possible to use the GSHF to locate

the zero of the discrete transfer function of the plant

in the position where the reference model has its

zero. This allows achieving the model matching

without carrying out a cancellation. The variable

GSHF parameters used to locate the discretization

zero in z=0.4 are p=0, s

=1, s

=0.5, c

(z)=-13.8528z

- 1.1708, c

(z) = 18.3565z + 2.3416 and d(z)=z. In

Fig. 5 is depicted the step response of the system

when the related design method is achieved.

As is shown in Fig. 5 with the use of GSHF the

matching with the reference model (16) is attained

IMPROVEMENT ON THE POLE-PLACEMENT CONTROL SCHEME BY USING GENERALIZED SAMPLED-DATA

HOLD FUNCTIONS

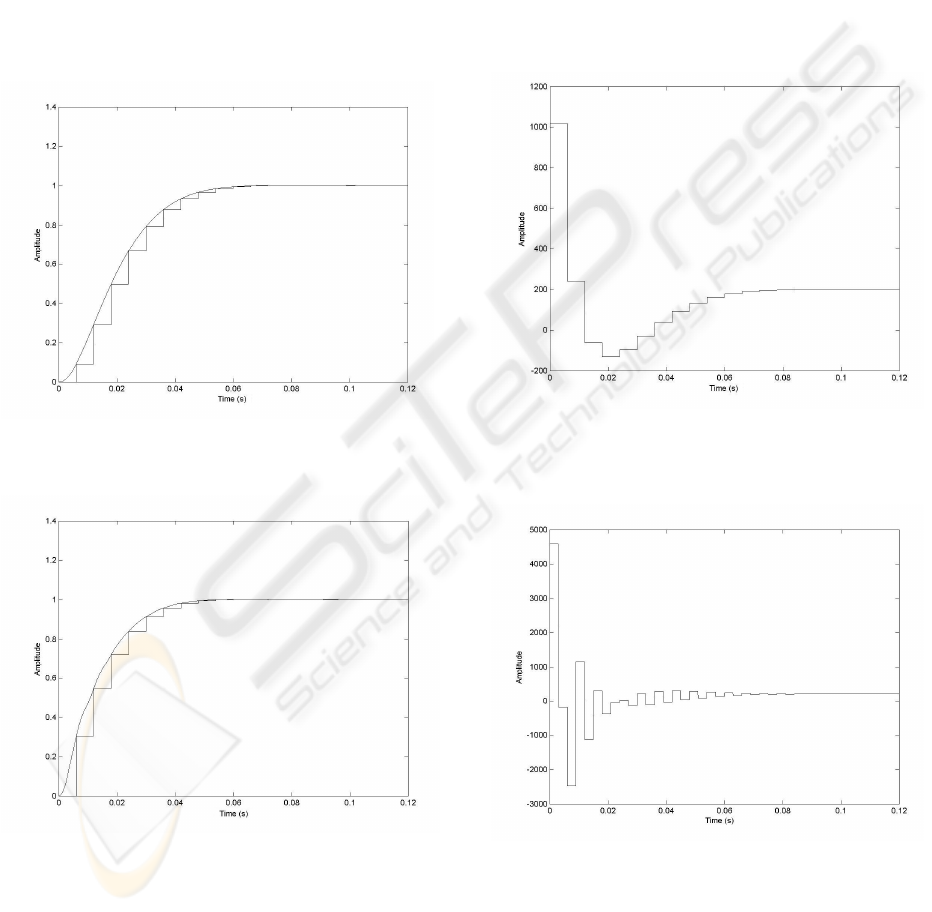
without incurring in the generation of the intersample

ripple that the system was having when in the control

scheme the reconstruction device employed was the

ZOH (compare with Fig. 3). Comparing Fig. 4 and

Fig. 5 it is noticed that to be able to fit the model

reference model (16) when the GSHF is used

supposes an improvement: No one of both responses

present overshoot, but while the system which

employs ZOH settles in 0.52 s. the system that uses

GSHF needs only 0.41 s.. This supposes an

improvement of 21% in the settling time.

On the other hand, if the zero is located with the

GSHF at z=-0.2 (p=0, s

=1, s

=0.5, c

(z)=-4.6707z –

0.3344, c

(z) = 6.6713z + 0.6687 and d(z)=z) and

then is cancelled with a controller pole, the step

response of the closed loop is almost the same to the

obtained one in the case where the zero was directly

located in z=0.4.

The control signals of the three designs are depicted

in Fig. 6, Fig. 7 and Fig.8. In that figures it is noticed

that the reduction of the settling time is obtained at

expense of amplification of the control signal. The

amplification of the control signal is quite big, and

therefore, it is important to decide, depending on the

application, if the improvement obtained justifies the

amplification the control signal suffers respect the

ZOH case, or not. It is important to notice that in this

paper only two subintevals (m=2) are taken into

account and may be possible, with the use of more

subintervals, to reduce the control signal amplitude

during the transient response. However, if the

number of subintervals used is very high the ZOH

contained in the GSHF is forced to work at high rate.

Figure 6: Control signal when the discrete plant zero is

transmitted to the reference model and ZOH is used.

Figure 4: Unit-step response of compensated system by

using ZOH device, when discrete plant zero is transmitted

to reference model.

Figure 7: Control signal of the design that uses the GSHF

to locate the zero in z=0.4 and this zero is transmitted the

discrete controller.

Figure 5: Unit-step response of compensated system by

using GSHF device to locate the zero in z=0.4 and this is

transmitted to reference model.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

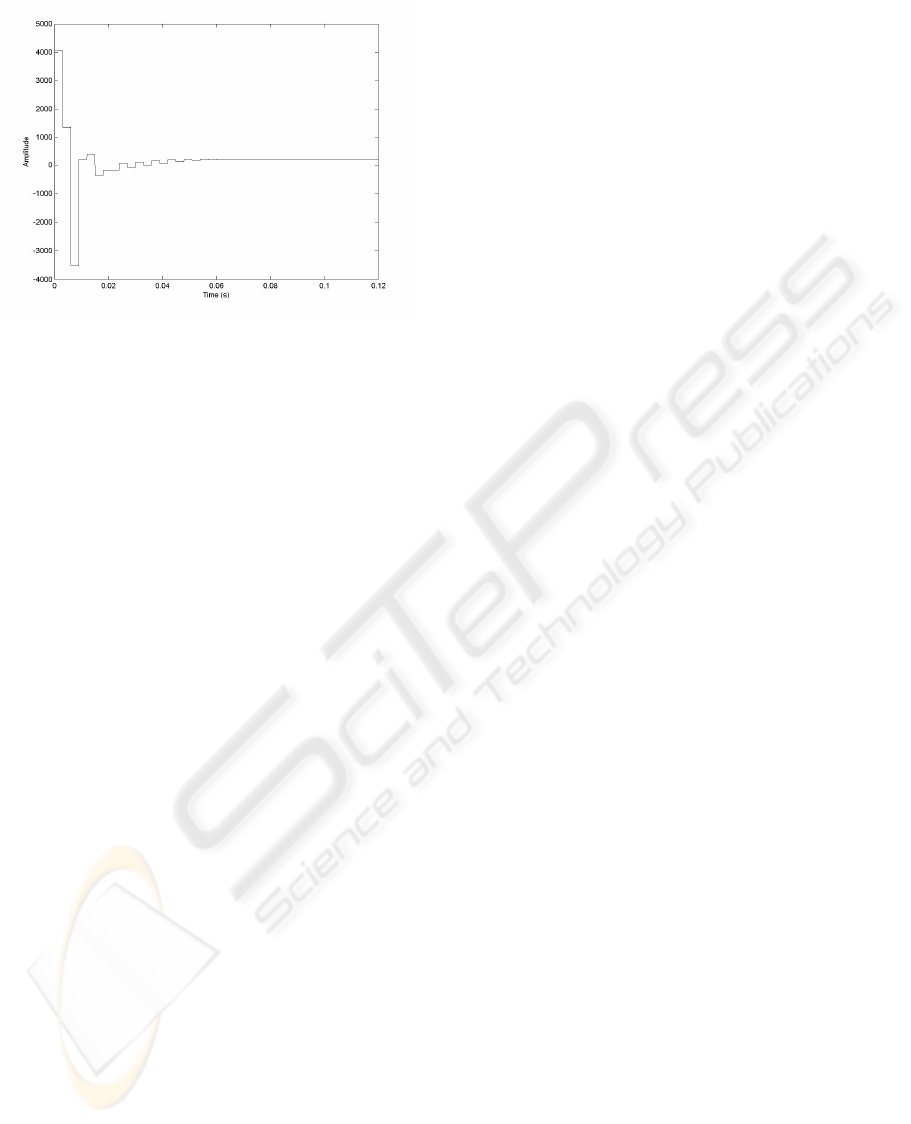
Figure 8: Control signal of the design that uses the GSHF

to locate the zero in z=-0.2 and this zero is cancelled by

the discrete controller.

5 CONCLUSION

In this paper, it has been noticed by means of an

application example that the variable GSHF can

improve the performance of the pole-placement

control scheme. The variable GSHF allowed us to

place the discretization zero of a second order

continuous plant in more beneficial location from the

viewpoint of the control strategy, improving in that

way the performance of the closed loop.

On the one hand, when the ZOH discretization zero

is sufficiently damped, it is possible to cancel it with

one of the controller poles and to locate the closed-

loop zero in the place where the reference model has

its zero. In such situations, the ZOH discretization

zero does not impose limitations to the attainable

performance and, therefore, the possibility of

relocating it that GSHF provides does not suppose

any advantage. On the other hand, when the ZOH

discretization zero is unstable or poorly damped,

which often happens when the sampling time used is

small enough (Aström et al., 1984), it is not advisable

to cancel it and, therefore, the performance that can

be attained by the classical design method is limited

given that the designer is forced to transmit such a

zero to the reference model in order to avoid

intersample ripple. This is the case studied in this

paper and it has been noticed that it is possible to

match the closed-loop discrete behaviour to the

reference model by the variable GSHF, without

generating intersample ripple.

From the carried out study it is concluded that the

GSHF ability to move the zeros can be used to

improve the transient response of a pole-placement

control. It has been also noticed that this

improvement is obtained at expense of the

amplification of the control signal during transient

state. It is important to point out that in this study it

has been used a variable GSHF with two subintervals

and it may be possible to reduce the control

amplitude by using more subintervals.

During the study, the possible deterioration of the

sensitivity functions, both discrete and hybrid ones,

have not been taken into account. That is one of the

possible drawbacks that the use of the GSHF can

generate (Freudenberg et al., 1997) and future

investigations on this device should integrate the

analysis of such functions.

REFERENCES

Kabamba, P. T., “Control of linear systems using

generalized sampled-data hold functions” IEEE Trans.

Automatic Control, Vol. AC-32, No. 9, pp.772-783

(1987)

Bai, E.-W., Dasgupta S., “A note on generalized hold

functions”, Systems & Control Letters, Vol. 14, pp.

363-368 (1990)

Er, M. J., Anderson B. D. O., “Discrete-time loop transfer

recovery via generalized sampled-data hold functions

based compensator”, Int. J. Robust Nonlinear Control,

Vol. 4, pp. 741-756 (1994)

Yan W.-Y., Anderson, B. D. O., Bitmead, R. R., “On the

gain margin improvement using dynamic

compensation based on generalized sampled data hold

functions”, IEEE Trans. Automatic Control, Vol. 39,

No. 11, (1994)

Rossi, M., Miller, D. E, “Gain/phase margin improvement

using static generalized sampled-data hold functions”,

Systems & Control Letters, Vol. 37, pp. 163-172

(1999)

Barcena, R., De la Sen, M., “On the sufficiently small

sampling period for the convenient tuning of

fractional-order hold circuits”, IEE Proc.-Control

Theory Appl., Vol. 150, No. 2 (2003)

Jury, E. I. “Hidden oscillations in sampled-data control

systems”, Trans. AIEE, 75, 391, (1956)

Clarke, D. W., “Self-tuning control of non minimum-

phase systems”, Automatica, 20, (5), pp. 501-517

(1984)

Kuo, B. C., (1992) Digital control systems, Saunders

College, 2

edn

Feuer , A., Goodwin G.C., “Generalized hold functions-

Frequency domain analysis of robustness, sensitivity

and intersample difficulties”, IEEE Trans. Automatic

Control, Vol. 39, No. 5, pp.1042-1047 (1994)

Freudenberg, J., Middleton, R., Braslavsky, J., “Inherent

design limitations for linear sampled-data feedback

IMPROVEMENT ON THE POLE-PLACEMENT CONTROL SCHEME BY USING GENERALIZED SAMPLED-DATA

HOLD FUNCTIONS

systems”, Int. J. Control, Vol. 61, pp. 1387-1421

(1995)

Freudenberg, J., Middleton, R., Braslavsky, J.,

“Robustness of zero-shifting via generalized sampled-

data hold functions”, IEEE Trans. Automatic Control,

Vol. 42, No. 12, (1997)

Hjalmarsson, H., Braslavsky, J.H., “Tuning of controllers

and generalized hold functions in sampled-data

systems using iterative feedback tuning”, In Proc. of

the IFAC 14th World Congress, Beijing, China,

(1999)

Chan, J.-H. H., “Stabilization of discrete system zeros: An

improved design”, Int. J. Control, Vol. 75, No. 10, pp.

759-765 (2002)

Chan, J.-H. H., “On the stabilization of discrete system

zeros”, Int. J. Control, Vol. 69, No. 6, pp. 789-796

(1998)

Aström, K. J., Wittenmark, B., “Computer controlled

systems. Theory an design”, Prentice Hall, (1990)

Franklin, G.F., Powell, J.D., Workman, M.L. (1992),

Digital control of dynamic systems, Addison-Wesley,

2nd edn.

Aström, K. J., Hagander, P., Sternby, J. “Zeros of sampled

systems”, Automatica, Vol. 20, No. 1, pp. 31-38

(1984)

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL