IMAGE BINARISATION USING THE EXTENDED KALMAN FILTER

Alexandra Bartolo, Tracey Cassar, Kenneth P. Camilleri

Department of Microelectronics

Simon G. Fabri

Department of Electrical Power and Control Engineering

Jonathan C. Borg

Department of Manufacturing Engineering

University of Malta

Keywords:

Feature Extraction, Image Processing, CAD.

Abstract:

Form design is frequently carried out through paper sketches of the designer’s mental model of an object.

To improve the time it takes from solution concept to production it would therefore be beneﬁcial if paper-

based sketches can be automatically interpreted for importation into three-dimensional geometric computer

aided design (CAD) systems. This however requires image pre-processing before initiating the automated

interpretation of the drawing. This paper proposes a novel application of the Extended Kalman Filter to guide

the binarisation process, thus achieving suitable and automatic classiﬁcation between image foreground and

background.

1 INTRODUCTION

Line drawing interpretation systems are used in en-

gineering design as an interface between engineer-

ing or architectural drawings and computer-aided de-

sign (CAD) tools (Ablameyko S. and Pridmore T.,

2000). Using similar principles, sketch recognition

systems are being developed since it is acknowledged

that designers can express their ideas more naturally

by means of sketches (Roth-Koch S., 2000). Recent

developments of such recognition systems have fo-

cused on online sketches obtained by means of PDAs

or tablet PCs. Since such systems are online, the in-

terpretation system has additional information about

the drawing, for example, pen position and velocity.

However, these systems lack the portability and ﬂex-

ibility of paper (Farrugia P. et al., 2004). In order

to achieve this ﬂexibility, the images must be pre-

processed, such that line data may be extracted from

the static image. Binarisation is one such process,

which compensates for the noise introduced by the

digitizing system. This work proposes the use of the

Extended Kalman Filter (EKF) to guide the binarisa-

tion of images as a step towards the automation of the

sketch recognition process which provides the neces-

sary data to control rapid prototyping and manufac-

turing equipment. The proposed method improves

the binarisation of poor quality images, whilst reduc-

ing the complexity of the threshold selection process.

This paper is divided as follows: Section 2 gives a

brief review of binarisation techniques, Section 3 in-

troduces the EKF and illustrates how this ﬁlter may

be used to identify a suitable threshold for binarisa-

tion. This is followed by the results in Section 4 and

conclusions in Section 5.

2 BINARISATION TECHNIQUES

Binarisation is the process by which grey levels

within an image are classiﬁed as either foreground or

background (Ablameyko S. and Pridmore T., 2000).

The selection of a suitable binarisation technique is

dependent on the type and quality of the images be-

ing used (Bulen S. and Mehmet S., 2004). Since

the sketched line drawing interpretation system that is

being developed is expected to process images from

the ﬁeld, it will typically process poor quality im-

ages, digitized using low-resolution devices, such as a

camera-phone. This requires a more detailed and lo-

cal analysis of the pixel distributions in order to select

a suitable threshold for pixel classiﬁcation. This sec-

tion describes ﬁve established binarisation techniques

originally proposed for line drawings and text images.

160

Bartolo A., Cassar T., P. Camilleri K., G. Fabri S. and C. Borg J. (2005).

IMAGE BINARISATION USING THE EXTENDED KALMAN FILTER.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 160-167

DOI: 10.5220/0001182101600167

 SciTePress

Palumbo and Guliano (Yang Y. and Yan H., 2000)

use a ﬁxed 9 × 9 window to evaluate the class of each

pixel within the image. The pixel value is determined

according to the ﬁve 3 × 3 local pixels within the

9 × 9 window centered on the pixel in consideration.

An initial threshold is used to determine the pixels

which deﬁnitely belong to the background whilst the

remaining pixels are classiﬁed using a different label

assignment rule requiring the speciﬁcation of three

additional user deﬁned parameters. Determining the

values of these thresholds is not straightforward since

they cannot be deduced from the image properties.

Niblack’s algorithm (Bulen S. and Mehmet S.,

2004) evaluates a threshold for each pixel within the

image according to the mean and standard deviation

of the pixels in a predetermined window W centered

at the pixel in consideration. The pixel class is deter-

mined as follows:

w(x, y) →



,p(x, y) <T(x, y)

,p(x, y) ≥ T (x, y)

(1)

where T (x, y)=µ(x, y)+k × σ(x, y), µ(x, y) is

the mean grey level of the pixels within the window,

σ(x, y) is the standard deviation of these pixels and k

is a user deﬁned parameter. Niblack’s algorithm re-

quires two user deﬁned parameters. The window size

determines the number of pixels from which the mean

µ(x, y) and standard deviation σ(x, y) are evaluated.

Thus, the window size should reﬂect the quality of the

image background, on which prior knowledge is un-

available. The value of k is used to adjust the amount

of print object boundary that is taken as part of the

foreground, and is therefore dependent on the quality

of the drawn line which is also an unknown quantity.

Eikvil’s method (Trier O. D. and Jain A. K., 2000)

is based on Otsu’s thresholding technique (Gonzalez

R. and Woods R. E., 2002), and makes use of two con-

centric windows L and S. The pixels within the larger

window L are temporarily classiﬁed into two classes

by Otsu’s threshold. The mean of these two clusters is

evaluated and their difference is compared to a para-

meter k which determines whether there there is sufﬁ-

cient contrast between the two clusters. This indicates

the effectiveness of Otsu’s threshold on the selected

region. Thus, if the difference between the two means

is larger than k, the pixels within the smaller window

are thresholded according to Otsu’s threshold. Other-

wise, the pixels are assigned to the class whose label

is closest to the mean grey level within the smaller

window S. This method requires the speciﬁcation of

three user deﬁned parameters, of which S and L de-

ﬁne window sizes, whilst k determines the threshold-

ing method applied to the smaller window. The size of

the smaller window S may be set to 3 which deﬁnes

the smallest window centered on a pixel. However,

the remaining parameters must be speciﬁed according

to the particular image properties.

Kamel and Zhao’s logical adaptive tech-

nique (Kamel M. and Zhao A., 1993) compares

the grey level of the pixel in consideration with

eight local averages in a pixel neighborhood of size

(2SW +1)

× (2SW +1)where SW represents

the stroke width of the line drawing. A comparison

operator is derived from these averages and is used

to determine the class of the pixel in consideration.

The algorithm requires two user deﬁned parameters,

namely the stroke width SW and an initial threshold

T which is used to evaluate the required comparison

operator. Yang and Yan (Yang Y. and Yan H., 2000)

proposed a method by which the two parameters

SW and T are calculated adaptively. However,

the adaptive evaluation of the parameter T requires

another parameter α. Yang and Yan (Yang Y. and Yan

H., 2000) specify a range of values of α for which

suitable values of T may be obtained.

Brensen’s method (Bulen S. and Mehmet S., 2004)

may either classify a single pixel or a group of pix-

els simultaneously according to the contrast present

within a selected window. The window’s contrast is

deﬁned as C(x, y)=Z

max

− Z

min

, where Z

max

and Z

min

are the maximum and minimum grey levels

within the window. If this contrast is smaller than a

predeﬁned value k, the pixels within the window be-

long to the same class, and the entire window may be

assigned to a single class. However, if the contrast C

is sufﬁciently large, then the pixels within that win-

dow belong to two different classes. Since the win-

dow has high contrast, a simple threshold based on

the average gray level may be used to classify the pix-

els within this window. Thus, the threshold T is de-

ﬁned as T (x, y)=

× (Z

max

+ Z

min

). This method

requires the speciﬁcation of parameter k which may

be evaluated adaptively using the method proposed

in (Bartolo A. et al., 2004)

2.1 Drawbacks

Although the above methods may yield results of con-

siderably good quality, the classiﬁcation processes re-

quires that a classifying criterion is evaluated for each

pixel in the image. Furthermore, these algorithms re-

quire the speciﬁcation of some parameter, such as a

window size in order to evaluate the threshold. Al-

though suggested values are speciﬁed for some algo-

rithms, better results are obtained after ﬁne-tuning the

parameter to the characteristics of the image under

test. Thus the performance of these methods is sus-

ceptible to image conditions. Methods for the adap-

tive evaluation for Brensen’s and Kamel & Zhao’s

methods have been proposed, but these require con-

siderable computational times, which slow down the

product prototyping process. In this paper, we attempt

to overcome these problems by modelling the sketch

as a trajectory being tracked in time.

IMAGE BINARISATION USING THE EXTENDED KALMAN FILTER

161

3 LINE TRACKING

A sketched drawing may be considered as a number

of lines which interact at junctions or corners to

create two-dimensional shapes. These lines may be

considered as distinct entities, which can be described

independently by some mathematical model. In this

paper, two mathematical models which describe the

position of a point on a line and its intensity are used

to enable line tracking. Each line stroke is modelled

as a trajectory propagating with a velocity v along a

line subtending an angle θ with the horizontal axis,

thus the position of the trajectory at a time instant

k +1is given by Equation (2), where x

and x

are

the vertical and horizontal coordinates on a plane.



(k +1)





(k)



+ v ×



sin θ

cos θ



(2)

Given a static, ofﬂine image, the velocity of propaga-

tion is irrelevant and may be assumed to be unity, thus

making the (x

) coordinates of the line dependent

only on the direction θ. The bilinear interpolation

relationship given by Equation (3) (Gonzalez R.

and Woods R. E., 2002), can be used to describe the

intensity of a pixel in terms of its (x

) coordinates,

z(k)=Ax

(k)+Bx

(k)+Cx

(k)x

(k)+D (3)

where A, B, C and D are interpolation coefﬁcients

derived from the four neighbors of a pixel in the image

with coordinates (x

In this way, each stroke in a given drawing may

be considered as a process modelled by Equation (2).

From the original image, measurements of pixel in-

tensities, given by Equation (3), can be obtained. By

considering the (x

) coordinates of each line as

the states of a dynamic system and the intensity val-

ues to be measurements obtained from noisy sensors,

Kalman ﬁlter theory (Maybeck P. S. , 1982) may be

used to estimate the system states and hence the coor-

dinates of points on each line.

Since the relation between pixel intensity and pixel

position, given by Equation (3), is not linear, the

Extended Kalman Filter (EKF) was adopted. The

EKF linearizes the state estimation around the cur-

rent estimate by using the partial derivatives of the

process and measurement functions to compute esti-

mates even when non-linearities are present. How-

ever, stability of the EKF assumes that the process is

linear around the current state (Maybeck P. S. , 1982).

3.1 The Extended Kalman Filter

In general, the EKF addresses the problem of estimat-

ing the state x of a discrete-time process modelled by

nonlinear state-space equations of the general form:

x(k +1) = f (k, u(k), x(k)) + w(k) (4)

z(k)=h(k, x(k)) + v(k) (5)

where w represents the model noise and v the mea-

surement noise, which are zero-mean, Gaussian noise

sequences of covariance Q and R respectively, u is

a known input, z is a measured output and f and h

are general non-linear functions. In our line sketching

application, the line generator model given by Equa-

tion (2) is cast into the state space form of Equation

4 to give Equation (6). Similarly, Equation (3) which

represents the intensity model, is cast into the state

space form of Equation (5) to give Equation (7).

x(k +1) = x(k)+ θ(k)+w(k) (6)

z(k)=h(k, x(k)) + v(k) (7)

where the state vector

x ≡



, ··· ,x



represents pen positions on n line strokes in the im-

age,

θ(k) ≡



sin(θ

), cos(θ

), ··· , sin(θ

), cos(θ

)



represents the orientation of the lines. The intensity

of the trajectories at time k, is given by z, which may

be written as:

(k)=A

(k)+B

(k)+

(k)x

(k)+D

+ v

(k)

(k)=A

(k)+B

(k)+

(k)x

(k)+D

+ v

(k)

(k)=A

(k)+B

(k)+

(k)x

(k)+D

+ v

(k)

where A

, B

, C

and D

are known constants ob-

tained from the bilinear interpolation, given by Equa-

tion (3).

Comparison between Equations (4) and (6) gives

f (k, u(k), x(k)) = x(k)+θ(k), and h(k, x(k)) is

given by Equation (3). Process noise w(k) models

any deviations from the ideal line stroke, and mea-

surement noise v(k) corresponds to noise affecting

the intensity measurements of the image.

Based on the state space model given by Equa-

tions (6) and (7), the EKF algorithm is used to ﬁnd an

estimate ˆx(k|k) to the actual state x(k), based upon

intensity measurements z(k) as follows (Maybeck P.

S. , 1982):

The Kalman Gain is deﬁned as:

K(k)=

P(k|k − 1)∇

h(ˆx(k|k−1))

∇

h(ˆx(k|k−1))

P(k|k − 1)∇

h(ˆx(k|k−1))

+ R

(8)

ICINCO 2005 - ROBOTICS AND AUTOMATION

162

where

∇

h(x)

≡

⎛

⎜

⎝

∂h

∂x

∂h

∂x

··· 00

00···

∂h

∂x

∂h

∂x

⎞

⎟

⎠

represents the rate of change in intensity in the verti-

cal and horizontal directions for each line stroke.

The state estimate is obtained by:

ˆx(k|k)=ˆx(k|k − 1)+

K(k)



z(k) − h(k, ˆx(k|k − 1))



(9)

where z(k) represents the true intensity measured

from the image and h(k, ˆx(k|k−1)) is given by Equa-

tion (3) evaluated at x(k)=ˆx(k|k − 1). The error

Covariance P(k|k) is given by:

P(k|k)=[I − K(k)∇

h(ˆx(k|k−1))

]P(k|k − 1) (10)

where the covariance prediction is:

P(k +1|k)=J

f (ˆx(k|k))

P (k|k)J

f (ˆx(k|k))

+ Q (11)

where J

f (x)

is the Jacobian matrix



∂f

∂x



, which in

this case is equivalent to the identity matrix from

Equation (6). The state estimate prediction at time

k +1is:

ˆx(k +1|k)=f (k, u(k), ˆx(k|k)) (12)

The EKF Equations (8) to (12) will recursively

compute the state estimate ˆx(k|k) for each iterate k,

given initial estimates ˆx(0|−1) = x

and initial co-

variance P(0|−1) = P

which represents the ini-

tial covariance of the error, reﬂecting the initial un-

certainty of the estimates.

3.2 Application to binarisation

The EKF equations described above, give the possi-

bility of locating points on a number of lines that form

part of the drawn object or objects in an image. In this

way, the EKF helps to discriminate between the image

foreground and background by selecting those pixels

which are located on lines and are therefore part of the

image foreground. The intensity of the pixels along

the tracked trajectory provides information about the

grey level intensities of the pixels forming part of the

line drawing. The mean grey level intensity µ

, and

standard deviation σ

of the tracked pixels can there-

fore be used to approximate the grey-level intensity of

the sketched object, and hence guide the binarisation

process. Since line pixels are darker than the back-

ground, the image pixels are classiﬁed by comparison

to a threshold T = µ

+ n × σ

,where n is a con-

stant which deﬁnes the tolerance to grey-level varia-

tions along the tracked line. Pixels whose intensities

are less than T may be classiﬁed as foreground line

pixels whilst the remaining pixels may be classiﬁed

as background pixels.

0 50 100 150 200 250 300 350

−0.15

−0.1

−0.05

0.05

0.1

Figure 1: The derivative of a horizontal row in an image.

Each positive - negative peak indicates the presence of a

line.

3.3 Implementation of the EKF

The implementation of the EKF requires suitable

starting points to initialize the line tracking process.

The position of the lines in a static image are un-

known, however, it may be assumed that part of the

image will be located towards the center of the im-

age. Thus, two scans along the horizontal and vertical

centerlines of the image are performed. The deriva-

tive of the grey level intensities of pixels lying along

this line is considered. The presence of a line is indi-

cated by a negative and positive peak along the track-

ing direction, which correspond to the two edges of

the line stroke as shown in Figure 1. Suitable start-

ing points may be taken at the midpoints of two such

peaks. Since a horizontal and a vertical scan are car-

ried out, the EKF can be initialized with at least two

starting points.

Since sketches are not necessarily built from

straight lines, but may have curves or lines that ex-

hibit a change in orientation, the sketched strokes are

modelled as piece-wise linear segments. This implies

that the line stroke may be built from a number of

short straight line segments which may be represented

by the state space model shown in Equation (6), thus

requiring the evaluation of the line orientation θ(k) at

each iteration k. This may be obtained by using Sobel

edge response (Gonzalez R. and Woods R. E., 2002),

which gives the magnitude response and the orienta-

tion of the pixels within the image. For edge pixels,

the magnitude response is highest and the pixel orien-

tation corresponds to the orientation of the line. Thus,

for each state ˆx, the closest edge pixel pair are located

and their orientation is used as an approximation for

the line direction θ(k).

The state estimates given by Equations (9) require

the evaluation of the intensity of the image at instant

IMAGE BINARISATION USING THE EXTENDED KALMAN FILTER

163

k. This may be obtained by searching for the darkest

gray level within a distance of one unit from the cur-

rent pixel position in the direction of θ +∆θ where

the ∆θ term is used to allow for deviations in the line

direction. Since the line strokes are expected to be

smooth, any line deviation from θ is accommodated

by seeking the darkest pixels in the cardinal directions

that enclose θ.

Since the EKF assumes that the model used is lin-

ear around the current state, large deviations from the

line stroke would cause the ﬁlter to diverge. For this

reason, it is required to terminate the tracking before

the ﬁlter diverges. An indication that the ﬁlter is di-

verging may be obtained by comparing the gray level

intensity of the tracked point with the grey level in-

tensity of background pixels. A measure of the back-

ground intensity may be obtained by taking the mean

gray-level m

of a sample of pixels located at a dis-

tance d perpendicular to the line direction, where d

should be greater than the stroke width of the sketched

lines. A point located on an image line will have a

gray level m

which is less than the mean gray level

of the sample pixels. Thus, divergence is indi-

cated when the mean gray level m

of the sampled

pixels is less than or equal to the gray level inten-

sity m

of the tracked point thus indicating that the

point is no longer on the sketched line and has moved

to a background region. This criterion also detects

when the tracking point arrives at the end of a line and

is therefore also used as a criterion to terminate the

tracking process once the end of the line is reached.

The image digitization process introduces some de-

gree of noise to the image such that adjacent pixels

will have variations in their gray level intensity even

though they belong to the same class. This will in-

troduce errors in the evaluation of the EKF starting

points since the derivative of an image row or column

will also reﬂect these intensity variations. For this rea-

son the image is low pass ﬁltered using a 3 × 3 mean

ﬁlter (Gonzalez R. and Woods R. E., 2002). This will

reduce the effect of the gray level variations in adja-

cent pixels making the transition between image class

more prominent in the row and column derivatives.

4 TESTING AND RESULTS

The proposed algorithm was tested under various con-

ditions and compared to the performance of the other

established methods discussed in Section 2. This sec-

tion shows the results obtained for a number of sam-

ple grey level images, whose gray levels are in the

range [0 256]. The visual results obtained by Kamel

and Zhao’s method are also shown in order to allow

a visual comparison. Kamel and Zhao’s method has

been chosen as this has the lowest number of user de-

Figure 2: Illustrating the tracking paths generated by the

EKF. White line segments indicate the tracked path, whilst

the darker lines indicate the image line strokes. This exam-

ple shows the tracking of 11 segments.

ﬁned parameters and thus offers the highest degree of

automation.

The ability of the EKF to track multiple lines was

ﬁrst tested with images having a low noise compo-

nent as shown in Figure 2. This shows an example

where the EKF tracks eleven segments, correspond-

ing to seven starting points detected from a horizontal

scan and four segments detected from a vertical scan

of the image.

The algorithm was then tested under varying de-

grees of measurement noise. This was introduced by

adding zero-mean Gaussian noise to the image. Fig-

ure 3 illustrates a ground truth image consisting of

4913 foreground pixels and 81651 background pix-

els. The corresponding noisy image is shown in Fig-

ure 3(b). The noise added has a standard-deviation

of 36 grey-levels, which corresponds to a signal-to-

noise ratio (SNR) of 12.8dB. The results obtained by

the EKF algorithm and Kamel and Zhao’s algorithm

are shown in Figure 3(c) and 3(d) respectively. Fur-

ther results are given in Table 1. These show that

the results obtained by the EKF algorithm have lower

Table 1: Comparison of percentage pixel error of the EKF

algorithm and Kamel and Zhao’s algroithm under different

noise conditions for the image shown in Figure 3(a). f→b

indicates the percentage foreground misclassiﬁcation and

b→f the percentage background misclassiﬁcation.

% pixel error

EKF Kamel & Zhao

SNR(dB) f → b b → f f → b b → f

18.08 7.1 0.53 17.9 0.79

16.20 14 0.07 26 1.19

14.54 12.2 0.18 35.8 1.59

12.79 2.9 0.97 44.7 1.9

ICINCO 2005 - ROBOTICS AND AUTOMATION

164

Table 2: Number of lines tracked and the sample points

considered, given as a percentage of the total number of

pixels in the image for the images shown in Figure 4

Image Lines Tracked % Points Tracked

4(a) 7 0.24

4(b) 4 0.27

4(c) 7 0.36

Table 3: Comparison of computational times with the al-

gorithms discussed in Section 2 for the images shown in

Figure 4

Computational Time (s)

Image 4(a) 4(b) 4(c)

EKF 57.3 26.3 55.9

Eikvil 75.2 73.7 75.4

Brensen 160 139.5 137.9

Kamel 78.6 78.8 70.9

Niblack 30.7 30.5 39.8

Palumbo 12.5 9.7 13

foreground misclassiﬁcations and background mis-

classiﬁcations in comparison to the results obtained

by Kamel and Zhao’s method. This indicates that the

EKF algorithm gives a better performance than that of

Kamel and Zhao under noisy conditions.

Figure 4 illustrates three images used to test the

algorithm. These include multiple lines and curves,

which illustrate that the line tracking process may

effectively track such images. The number of lines

tracked and the sample points taken is tabulated in Ta-

ble 2.

This indicates that the thresholding decision is

based on a small number of pixels, which however,

correspond to pixels directly related to the image fore-

ground. The binary result obtained for these images

is illustrated in Figure 5. The results obtained may

be compared with those illustrated in Figure 6, which

are obtained by using Kamel and Zhao’s algorithm

after manually determining the most suitable values

for α. These results show that the proposed EKF al-

gorithm gives results whose quality is comparable to

those given by other binarisation thechniques. Fur-

thermore, Table 3 shows that the proposed binarisa-

tion process requires lower computational times than

Brensen’s and Kamel & Zhao’s methods, for which

adaptive parameter evaluation was applied. Although

Niblack’s, and Palombo and Guiliano’s methods show

lower computational times, this does not include the

time required to ﬁnd suitable parameters for each im-

age, because, these are not adaptive methods.

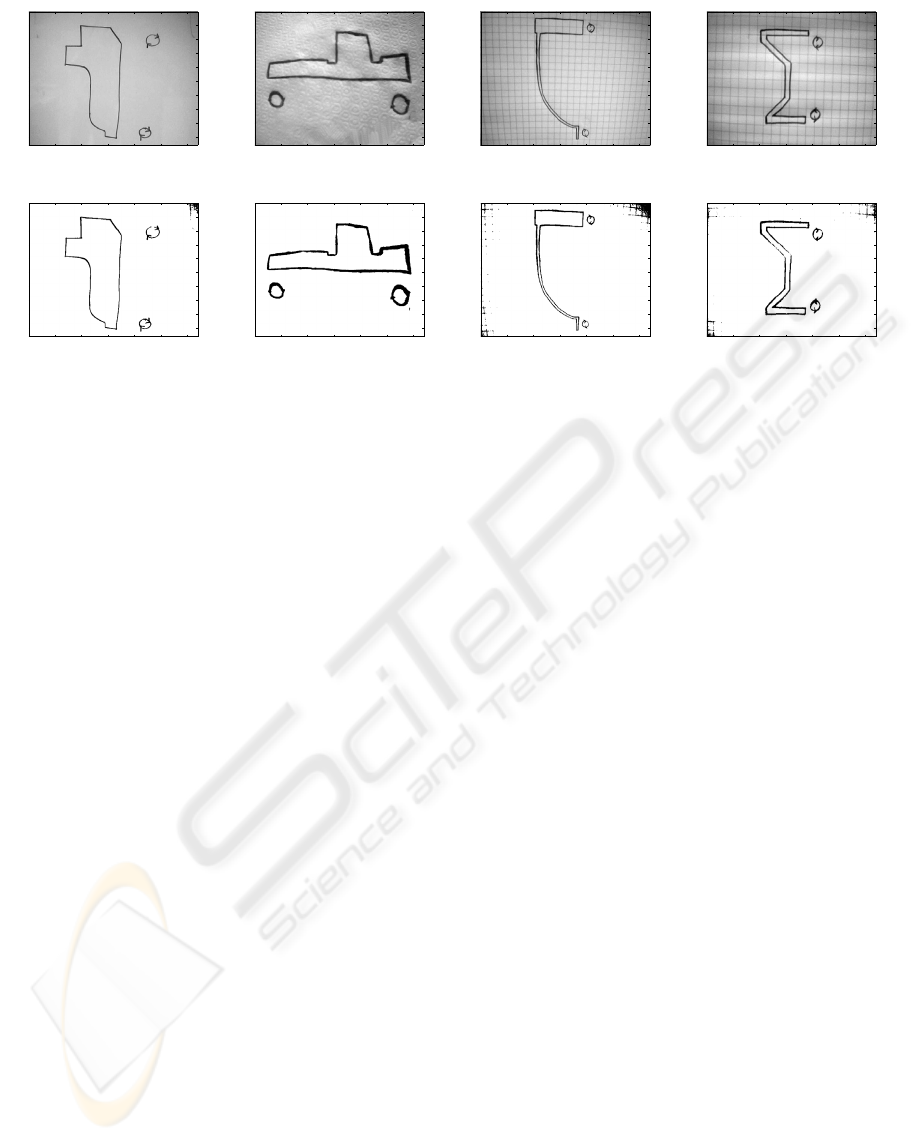
The algorithm was also tested on images captured

by a cameraphone at a resolution of 96 dpi. A sam-

ple of these images is shown in Figure 7 where Fig-

ure 7(a) shows an image drawn on plain white paper,

Figure 7(c) shows an image drawn on textured tissue

paper whilst Figures 7(e) and 7(g) show images drawn

on graph paper. Note that the cameraphone captures

the light reﬂections on the image such that the result-

ing digital images display variable gray-level inten-

sities along the background. This is particularly ev-

ident in the image corners, where the gray-level in-

tensity of the background is comparable to that of the

foreground. The performance of the EKF algorithm is

comparable to that of the algorithms discussed in Sec-

tion 2 but require smaller computational times. Fig-

ure 7 shows how the algorithm correctly identiﬁes the

foreground pixels. Of particular importance is the

distinction made between the image foreground and

the background grid in Figures 7(e) and 7(g), which

allows the extraction of the object from interfering

backgrounds. Some misclassiﬁcation of the back-

ground pixels in the corner regions occurs for images

in Figure 7(f) and 7(h). This is due to the fact that the

image is being thresholded with a global threshold.

The images shown in Figure 7(f) and 7(h) have some

foreground pixels with a relatively high gray level in-

tensity, resulting in a higher valued threshold, which

will classify the darker background regions as fore-

ground.

5 CONCLUSION

The proposed EKF binarization method has been

shown to yield good quality results that are compa-

rable to those obtained by existing methods. Further

work is being carried out in order to apply the algo-

rithm to local image regions, resulting in a number of

local thresholds rather than a single global threshold.

This will reduce the effect of global thresholding, thus

further improving the results obtained.

The proposed method offers a higher degree of au-

tomation than the other binarization techniques dis-

cussed since no user deﬁned parameters are required.

This helps to improve the rapid prototyping process

of the sketched line drawing, which is the main, long

term objective of this work.

ACKNOWLEDGEMENTS

This work has been mainly supported by Grant 73604

of the University of Malta.

IMAGE BINARISATION USING THE EXTENDED KALMAN FILTER

165

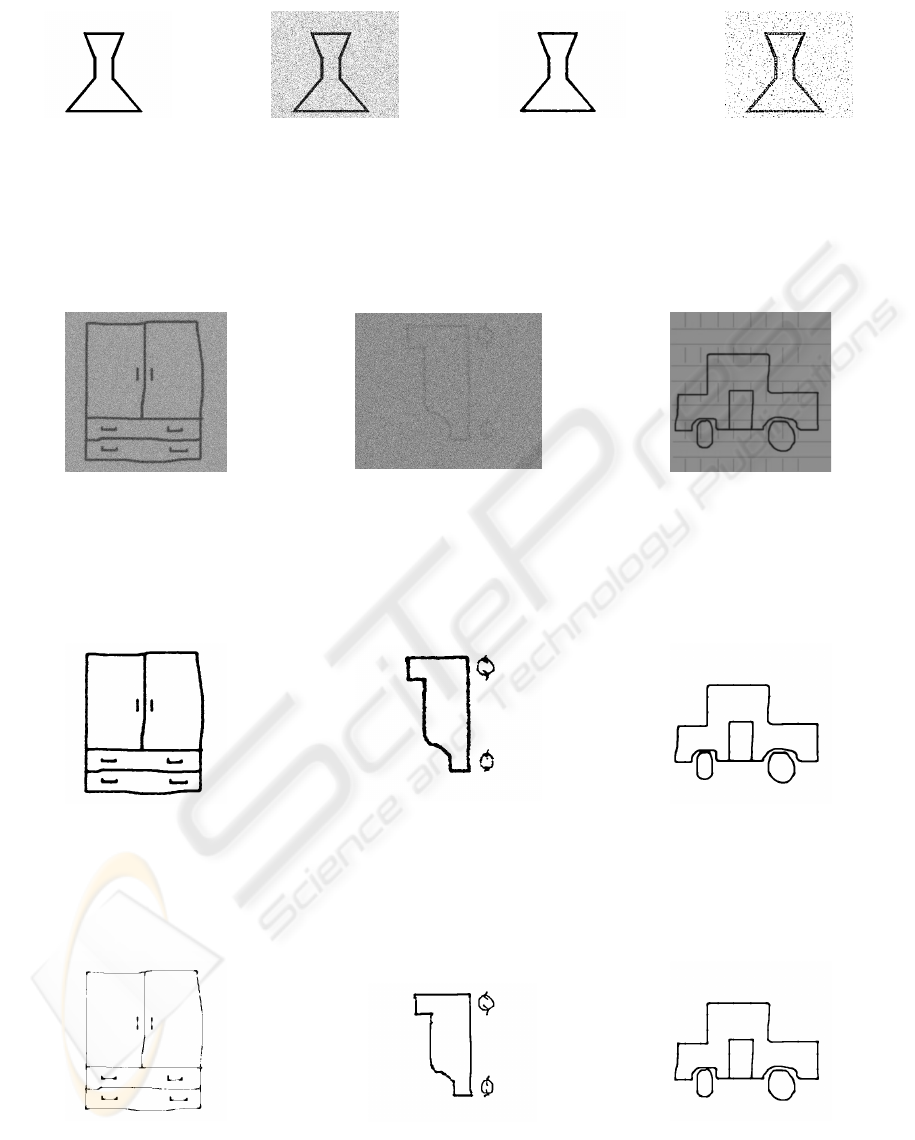
(a) (b) (c) (d)

Figure 3: Illustrating the performace of the EKF binarisation under noise. Figure (a) shows a ground truth image and Figure

(b) shows the corresponding image with added Gaussian noise resulting in an SNR of 15.5dB. Figures (c) and (d) show the

binary result obtained by the EKF method and Kamel & Zhao’s method respectively.

(a) (b) (c)

Figure 4: Sample test images. Images (a) and (b) illustrate image having a homogenous background with dynamic ranges of

160 and 80 respectively, whilst Image (c) is an example of an image having background artefacts.

(a) (b) (c)

Figure 5: Results given by the EKF binarisation for images shown in Figure 4.

(a) (b) (c)

Figure 6: Results given by Kamel & Zhao’s method for images shown in Figure 4, with α equal to 0.4, 0.2, 0.1 respectively.

ICINCO 2005 - ROBOTICS AND AUTOMATION

166

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

100 200 300 400 500 600

100

150

200

250

300

350

400

450

(g) (h)

Figure 7: Results obtained by the EKF binarisation algorithm for a set of real test data captured with a cameraphone using a

resolution of 96 dpi. Figures a), c), e) and g) show the original images whilst Figures b), d), e) and h) show the binary result.

REFERENCES

Ablameyko S. and Pridmore T. (2000). Machine Interpre-

tation of Line Drawing Images. Springer-Verlag.

Bartolo A., Camilleri K., Borg J., and Farrugia P. (2004).

Adaptation of Brensen’s Thresholding Algorithm for

Sketched Line Drawings. Eurographics Workshop on

Sketch-Based Interfaces and Modeling, pages 81–90.

Bulen S. and Mehmet S. (2004). Image Thresholding Tech-

niques - A Survey over Categories. Journal of Elec-

tronic Imaging, 13:146–165.

Farrugia P., Borg J., Camilleri K., Spiteri C., and Bartolo

A. (2004). A Cameraphone-Based Approach for the

Generation of 3D Models from Paper Sketches. Eu-

rographics Workshop on Sketch-Based Interfaces and

Modeling, pages 34–42.

Gonzalez R. and Woods R. E. (2002). Digital Image

Processing. Prentice Hall.

Kamel M. and Zhao A. (1993). Extraction of Binary Char-

acter/Graphics from Grey Level Document Images.

CVGIP: Graphical Models and Image Processing,

55(3):203–217.

Maybeck P. S. (1982). Stochastic Models, Estimation and

Control, Volume 2. Academic Press.

Roth-Koch S. (2000). Generating CAD Models from

Sketches. Proceedings of the IFIP WG5.2 Geomet-

ric Modeling: Fundamentals and Applications, pages

207–219.

Trier O. D. and Jain A. K. (2000). Goal directed evaluation

of binarisation methods. Workshop on Perfromance

versus Methodology in Computer Vision, 17(3):209–

217.

Yang Y. and Yan H. (2000). An Adaptive Logical Method

for Binarisation of Degraded Document Images. Jour-

nal of the Pattern Recognition Society, 33:787–807.

IMAGE BINARISATION USING THE EXTENDED KALMAN FILTER

167