A COMPUTER ORIENTED ALGORITHM FOR ANALYZING

LIMIT CYCLES IN DISCRETE CONTROL SYSTEMS

M. Utrilla-Manso, R. Jiménez-Martínez, R. Mallol-Poyato,

J. Sánchez-Golmayo and F. López-Ferreras

Departamento de Teoría de la Señal y Comunicaciones, Universidad de Alcalá

CRTA.Madrid-Barcelona km. 33.6, Alcalá

de Henares, Spain

Keywords: Limit cycles, quantization, discr

ete control system.

Abstract: In this paper a new and fast algorithm for characterizing the behaviour of zero-input limit cycles that can

appear in digital control systems when finite precision computer is used. This proposed algorithm suggests a

practical approach to determine the impact of these parasitic oscillations against difficult theoretical

solutions limited to simple systems and very conservatives in some cases. This algorithm is applicable to

any kind of discrete system described by its difference equations and quantized by any quantization scheme

and supply practical results in considerable less time that other exhaustive formulations. Some tables show

the feasibility of the algorithm compared with exhaustive searches and theoretical calculations to

characterize the limit cycles and its applicability for any kind of discrete system as different digital filters

and digital control systems where different controllers are applied

1 INTRODUCTION

It is known that algorithms for digital control are

implemented in microprocessors or microcontrolers

whose internal registers have a length of 8, 16 or 32

bits. This finite precision leads in errors due to the

quantization of all values to be stored, such as, input

signal, coefficients of systems and internal

calculations. Besides, the internal representation of

values in that oriented hardware is used to be in

fixed point, so the dynamic margin for values

decreases over other floating-point schemes.

That lost of information yields three important

oblems for the whole system performance:

sensitivity of the coefficients, quantization errors in

each internal storage node and the output, and some

possible oscillations at the output and internal nodes

called Limit Cycles (LC). The first one is a

deterministic matter so that the quantization process

moves the poles and ceros from these original

positions. The design must guarantee that the

magnitude of quantized poles is inside unit circle

and its movement does not impair the final

performance of the algorithm. The other problems

are not deterministic matters, so the study is used to

be analytic, based on statistical considerations or by

mean of computer simulations of the system.

This paper focuses the study of one of the

oblems derived from finite precision arithmetic,

the limit cycles. These are oscillations appeared at

the output and internal registers when the input is

zero or a constant. This problem can be especially

important in control systems, where the controller

could give non-zero signal to the system even

though the input signal is zero (Slaughter, 1963),

(Phillips, 1990). Greater oscillations can appear

when internal register values overflows and is not

saturated to the maximum value, so the system must

be conveniently scales to avoid this effect.

The main goal of this paper is the study and

characte

rization of possible limit cycles that can

appear at the output or internal storage nodes of the

digital control system, by mean of simulation

algorithms on a computer. The system under study is

shown in figure 1 that presents the overall system

where appears the discrete equivalent of the

controller that is usually implemented on a

microcontroler under finite precision arithmetic.

Figure 2 shows the simulated system, where only the

controller must be quantized.

Earlier studies present different structures to

estab

lish the controller (Franklin, 1997), (Ogata,

1996), (Phillips, 1990) that yield different results

155

Utrilla-Manso M., Jiménez-Martínez R., Mallol-Poyato R., Sánchez-Golmayo J. and López-Ferreras F. (2005).

A COMPUTER ORIENTED ALGORITHM FOR ANALYZING LIMIT CYCLES IN DISCRETE CONTROL SYSTEMS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 155-160

DOI: 10.5220/0001182401550160

 SciTePress

under finite precision. So the analysis of this

performance under finite arithmetic must be an

integral part of the design process.

System

Sensor

c(t)

u(t)

Difference

equations

Clock

ZOH

r(kT)

e(kT)

y(kT)

u(kT)

y(t)

A/D

Digital regulator

r(t)

Figure 1: Discrete equivalent controller

Controller

(z)

System

G(z)

Sensor

r(k)

e(k)

c(k)

y(k)

w(k)

Figure 2: Equivalent discrete for simulating in computer

Limit cycles is a topic widely studied by earlier

researchers. Up to the moment most of these studies

were theoretical approaches, looking for maximum

bounds for each internal register while a limit cycle

is present (Bauer, 1991), (Premaratne, 1995),

(Green, 1988), (Yakowitz, 1973), (Djebbari, 1998).

However these schemes need certain structures as

state space (Bauer, 1991), (Premaratne, 1995) to use

the matricial representation for calculations. Besides

they lead to conservative results and they in general

are applicable for low order filters or systems

(Slaughter, 1963), (Phillips, 1990). High order

systems are very difficult to analyse by these

methods. Earlier studies use the computer to

simulate the real behaviour of the system under

finite precision (Bauer, 1991), (Premaratne, 1995)

but they suggest exhaustive algorithms where a great

amount of state vectors are tested. Besides most of

them require certain structures, rounding strategies

and mainly are only useful for low order filters

because the high computer time they take.

In this paper a partial search algorithm is

presented, where the choice of state vectors to

analyse is strategically selected by the results

obtained up to the moment for the vectors still

analysed. The proposed algorithm is also applicable

for analysing any discrete system since the

difference equations are used to describe the real

system.

The paper is organized as follows. The section 2

shows the representation for discrete systems to be

analysed by a computer, quantization schemes and a

detailed explanation for the proposed algorithm. The

section 3 presents results that show the feasibility of

the algorithm to be used for different digital filters

and then for discrete control systems. Section 4 ends

with some conclusion for the use and applicability of

the proposed algorithm over other approaches.

2 PROPOSED ALGORITHM

2.1 Discrete system representation

To develop an algorithm for analysing zero input

limit cycles we suggest using the difference

equations to describe the performance of the digital

system. In this way we can get access to the

information of the internal representation of the

system. This is an important key to simulate the real

performance of the system for analysing not only

limit cycles but also any quantization problem like

noise and overflow in each node.

The only problem is to order the internal nodes

of the system to obtain a computable difference

equation in each node where for obtaining the

following value in we only have to consider

preceding values of other nodes (Diniz, 2002).

Complying with considerations in (Diniz, 2002) and

reordering the whole system we conclude that:

(1) (1) (

jmjmmj

)

kaxkbx

+= ⋅ ++ ⋅

∑

)

(1)

Where:

• N: order (number of internal computable

nodes) of the system.

• j: node of computation.

•

:value of j

node in the

following time k+1.

•

: transmission coefficients of the

branch connecting node m to j.

mj mj

Notice the in equation (1) zero input is

considered and with conveniently ordering of

internal nodes

=0 for m≥j, so all the recurrence

equations only need values of internal signals still

calculated.

Under fixed-point arithmetic, equation (1) turn to

(2):

(1) (1) ()

mj mj

kQaxkbxk

⎡

⎤

+= ⋅ ++ ⋅

⎢

⎥

⎣

⎦

∑

(2)

where Q is the quantization process and

is the

quantized value in node j. Note that in (2) double

precision accumulator is considered since there is

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

156

only one quantization, that is the whole sum of all

products.

The quantization processes considered in this

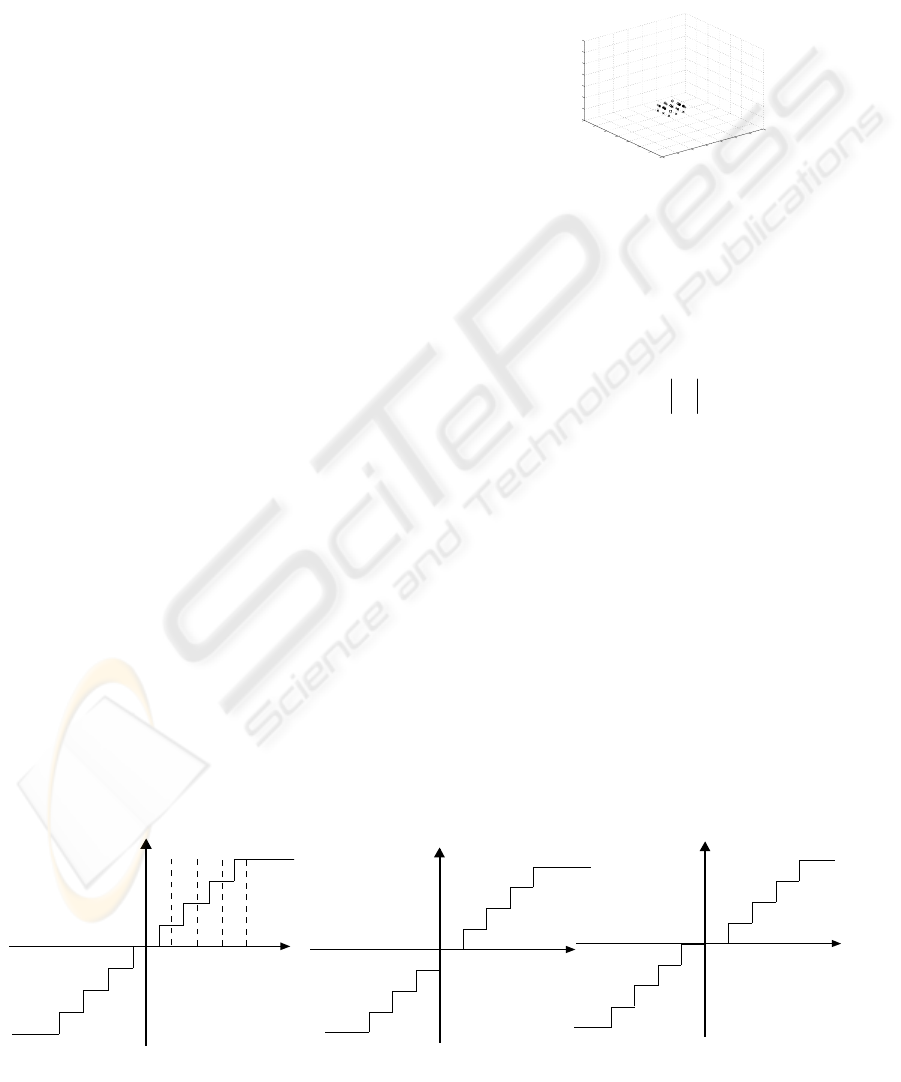
paper are shown in figure 3, where

is the

quantization step size and B is the number of bits

used. Case (a) is the most natural quantization in

microcontrolers, called two’s complement truncation

−+

(TC2), case (b) is Signed Magnitude Truncation

(SM) and case (c) is Rounding (RD). These are the

schemes analysed in this paper but the representation

proposed allows using any other one because of

getting access to the value in each real node

programmed in the hardware.

2.2 Description of the algorithm

The proposed algorithm for checking the behaviour

of the zero input limit cycles is based on

experimental results obtained after analysing many

filters under exhaustive searches as in (Bauer, 1991),

where it has been observed that all limit cycles

detected present low amplitudes and are confined in

a closed region in the n-dimensional space (N is the

number of inner register in the filter). Figure 4

shows this typical situation (each axis shows the

amplitude stored in each register in entire multiples

of quantization step size q). This sentence meets

with demonstrated theoretical bounds on amplitude

in each internal registers obtained by some

researches (Bauer, 1991), (Premaratne, 1995),

(Green, 1988), (Yakowitz, 1973). Therefore it seems

to be not worthy to check toward limit cycles to all

possible state vectors up to a conservative theoretical

bound as in exhaustive algorithms (Bauer, 1991),

(Premaratne, 1995), (Djebbari, 1998). Checking only

a particular set of state vector could yield results

very closed to exhaustive formulations but in a

considerable less time.

The proposed algorithm tries to select a reduced

set of state vectors to test for the convergence

toward a possible limit cycle. This set will be

smaller than the one formed by all possible state

vectors up to a theoretical bound calculated for

exhaustive formulations.

For selecting this set of vectors we suggest to

divide the search process in two stages, with two

subsets of vectors: one called fixed-stage and other

called guided-stage.

The aim of the first stage is to place the search in

the region of all limit cycles are confined. This point

establishes the beginning of a more accurate search

in this confined region where probably we will find

all limit cycles.

−7

−5

−3

−1

−7

−5

−3

−1

−7

−5

−3

−1

Figure 4: state vectors reached in all limit cycles

Fixed-Stage

The main aim for this stage is to place the search in

the unknown region where it is demonstrated that all

LCs are presented (Bauer, 1991). Therefore we

choose a set of state vector for this first stage

{

}

{

}

{

}

()

/2,0

0,1,..., 1; 1, 2,..., ;

Fjj

where

nBjN

γγ

⎧

⎪

⎨

⎪

=−=

⎩

−

This set consist of all state vectors x with infinite

norm equal to 1 and all vectors obtained by

multiplying each element by the scalar

2 , for n

from 0 to N. Therefore the process tests more state

vectors with low infinite norms, where is more

probable that limit cycles are placed. Once this set

has been tested, the process obtains all state vectors

belonging to limit cycles, set or vectors called O,

and, from it, the maximum bound in each internal

node. That is the bound vector M. This value is the

-1

Q [x ]

-4q

-3q

-2q

-q

(a)

-1

Q [x]

-4q

-3q

-2q

-q

(b)

-1

Q[x]

-4q

-3q

-2q

-q

(c)

Figure 3: quantization schemes considered

A COMPUTER ORIENTED ALGORITHM FOR ANALYZING LIMIT CYCLES IN DISCRETE CONTROL SYSTEMS

157

beginning for the next stage, suggesting that we

could find limit cycles of greater infinite norm.

Therefore now the process make a deeply search in

this region.

Guided-Stage.

As we know that all LCs are placed very closed one

to another in the N-dimensional region, where

probably we are from the first stage, this stage

suggest to test all vectors resulting of multiply all

elements of the set formed by x such as

|| || 1

∞

by n=

. This bound M is updated in the

stage and leads the process, so the LCs detected

guides the set of vectors to test. The process ends

when have been tested vectors with infinite norm h

times greater the maximum bound found at the

moment. In this case we consider out of the region

of LCs. So, this stage suggests a subset of vectors to

test

|| 1

∞

()n

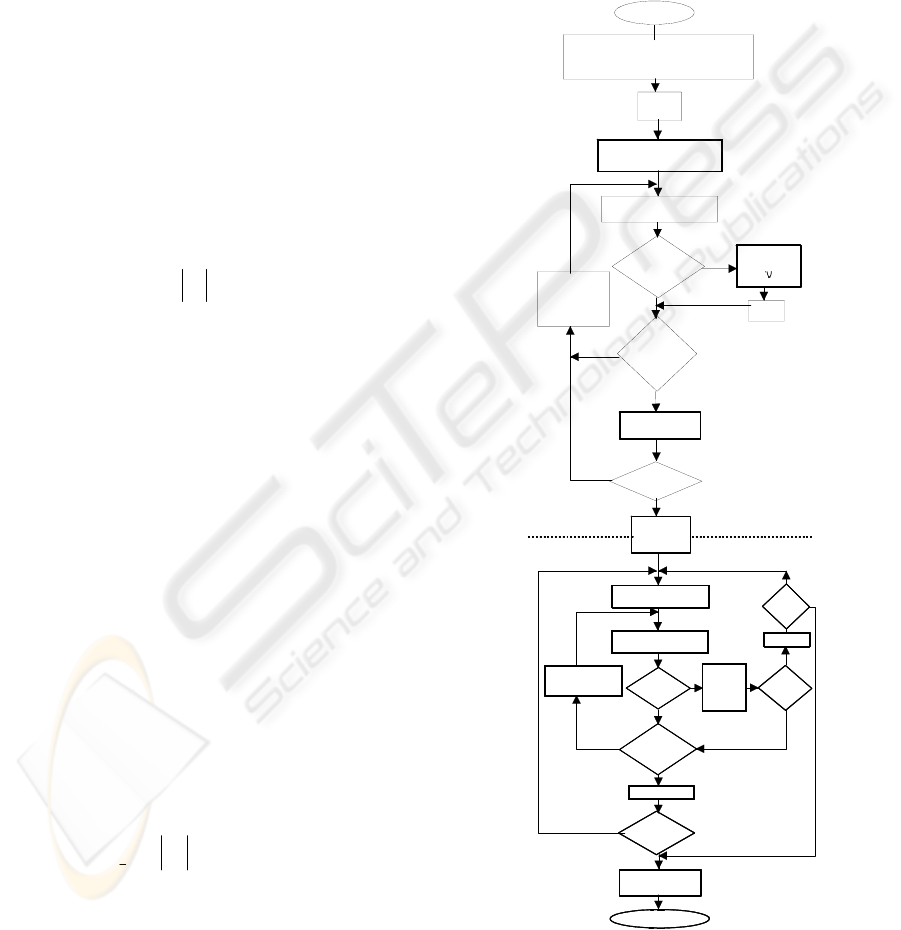
The flowchart in figure 5 shows the process, where

the nomenclature used to described it is:

 B: number of bits used in implementation.

 q=2

-B+1

: quantization step size. All

information in each register and output is

normalized to this number.

 N: number of inner registers of the filter.



{

}

123

... ...

xx x x=x

state vector or set

of quantized values in all internal nodes.

 h: free parameter to guarantee the robustness

of the algorithm (in the results obtained h=3).



; i is the

order of the different limit cycles detected.

{}

/ belongs to a limit cycle

O = xx

 O=

is the set of all different limit

cycles.



{

}

max

∀∈

x; =⎨x

⎬, j=1,2,...N;



{

}

; i=1,2,...N. Practical bound.

The only problem is to detect the possible limit cycle

from a certain state vector. This is the box called

“Test of convergence” in the flowchart. We use the

procedure described (Utrilla, 2000), that is the

fastest of the papers at the moment (Bauer,

1991)(Premaratne, 1995), (Djebbari, 1998). This

procedure suggest make iterations with the

difference equations and zero input comparing with

zero vector and the initial one. If some iterations

have been made without finding anything we update

with the current state vector because probably we

are in the transient state. Considerations about

number of iterations and updating are detailed in

(Utrilla, 2000).

Input:

Type of quantization

System described by difference equations

n = 0;i=0

Generate

Limit

cycle

detected?

Generate

the next

vector in

||M||

Generate the first element of

(n)

Test for the convergence

Detected limit

cycle?

Tested all vectors

n = n +1

n > ||M|| +h

∞

End

Generate the following

vector of

Generate the

orbit

Update M

O ,

∞

n=||M|| +1

Yes

Increased

||M|| ?

Yes

n > ?

∞

Evaluate O

Obtain

∞

(n)

Get the first state vector

(n)

Test for the convergence

i=i+1

Al vectors

checked?

(n)

n=n+1

Have been

checked all vectors

in ?

Yes

With O, obtain M,P, C

B-1

n > ?

B-1

Start

{

}

{}

{

}

()

/,0,

: 1, 2,..., ; 1, 2,3,..., 2

Gjj

xx n n

where j N n

γγ

−

⎧

== ∈ − −

⎪

⎨

⎪

⎩

Figure 5: Flowchart of the proposed algorithm

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

158

The result of the whole process is a set of all

vectors belonging to LCs called O. So we can obtain

all the information we need about the behaviour of

the system on behave to limit cycles, that is

maximum practical bound M, output in LCs C and

period of them P.

3 RESULTS

3.1 Digital Filters

Due to the feasibility of the algorithm to analyze any

digital system characterized by its difference

equations, many digital filters have been analysed to

study their behaviour about LCs under different

quantization schemes. Also comparative studies

have been made with theoretical calculations

(Yakowitz, 1973) and exhaustive search algorithms

(Bauer, 1991), (Premaratne, 1995) with certain

improvements realized in (Djebbari, 1998) and

(Utrilla, 2000) for detecting a possible LC from a

state vector. Some representative results are shown

in Table 1. This table presents the too conservative

theoretical bounds on amplitude against the real

bounds obtained by exhaustive search algorithms.

However, as the table shows, this approach takes

long time analyzing irrelevant state vectors.

Table 1: Different digital filter analysed

This table shows the applicability of the proposed

algorithm to analyse the behaviour of any discrete

system over zero input limit cycles against

theoretical calculations and exhaustive schemes. So

it can be used as a integral part of design process

when fixed-point arithmetic is used.

3.2 Digital control systems

Digital control systems as in figure 2 can be

represented by its difference equations and therefore

can be analysed its limit cycles behaviour by the

algorithm proposed in this paper. Due to the reduced

time to analysis, it should be used to select the best

representation for the discrete controller, although

all of possible cases performs the same control under

infinite precision.

In this paper has been analysed the system

presented in the figure 6 (Slaughter, 1963)

Figure 6: Digital Control System

0.402 0.202 0.020

()

1 0.099 0.034

−

−−

−+

123

0.382 0.754 0.09

()

1 1.503 0.552 0.05

−−−

−+ −

()ek ()ck()rk

−

The controller has been implemented by

structures obtained from (Phillips, 1990) in the

known forms 1D, 2D, 3D and 4D, each analysed the

LCs under finite precission of 8 bits, saturation

(SAT) and overflow (OV) and Rounding (RD),

Two’s complement (TC2) and Signed Magnitude

(SM) truncation schemes.

The system has been implemented with two

cascade structures of 2

and 1

order. This is no

matter due to this part of the whole system has not

been quantized since it represents a continuous time

system. But its performance has an important

influence on the whole discrete system. All these

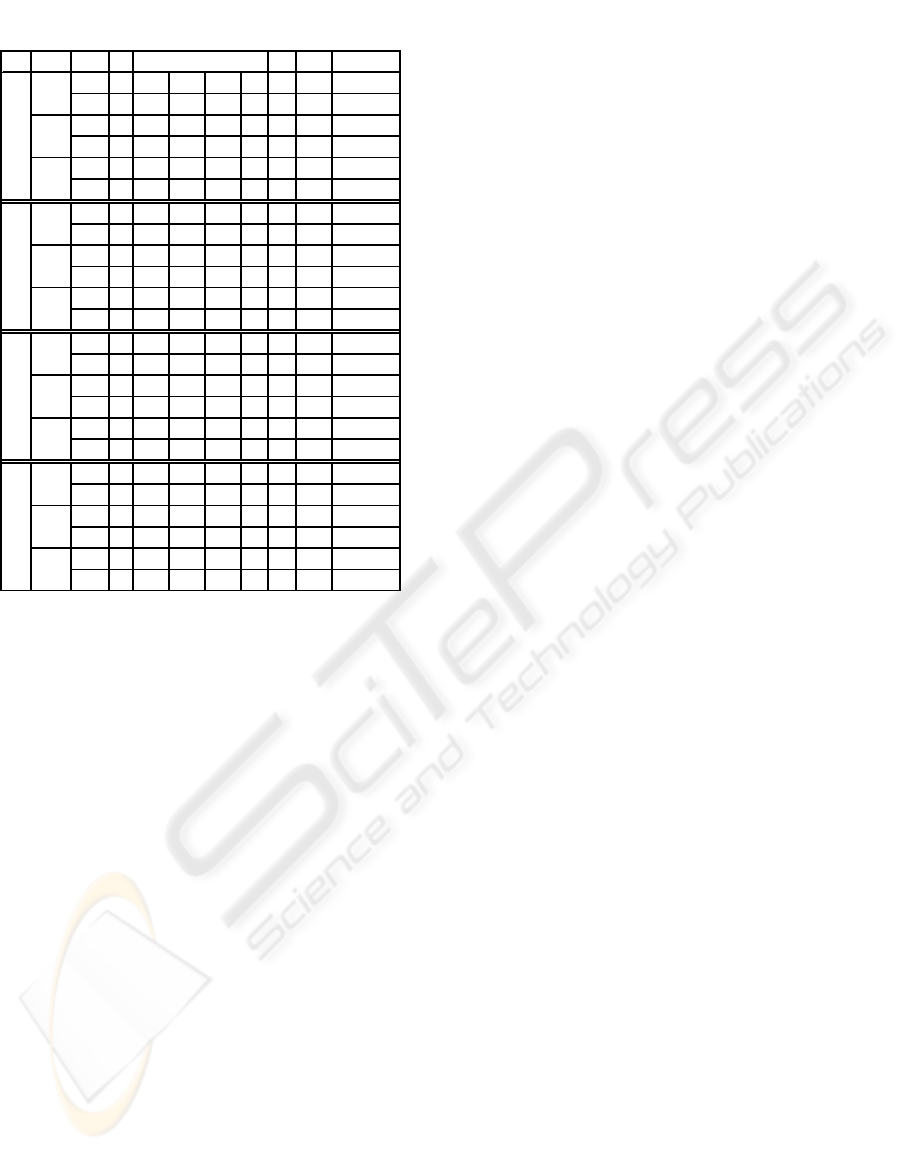
analysis are presented on table 2, where is shown the

feasibility of the algorithm to test this type of control

systems. This table presents the maximum bound

obtained from the algorithm M (in multiples of

quantization step size q), period of the worst limit

cycle detected (T), maximum output in zero input

limit cycles (C) and time in seconds taken in the

analysis. The table shows the great difference

between the data by saturation or overflow, and

under the low amplitude of limit cycles under

saturation, as we still suggested. An important

difference is the behaviour under SM truncation,

since limit cycles are lower or even are free of them.

That is a rational event due to the characteristic of

this truncation.

Approach T C

TIME

(secs)

Theoretical 131622

Exhaustive alg. 1 1 1 3 0 23

Proposed alg. 1 1 1 3 0 0,12

Theoretical 53473119

Exhaustive alg. 2110 42 818

Proposed alg. 2110 42 0,36

Theoretical 33351721

Exhaustive alg. 1111 40 481

Proposed alg. 1111 400,701

Theoretical 3640192533

Exhaustive alg. 3444474 307

Proposed alg. 3444474 2,37

Laticce in state

varibles, Elliptic,

N=5, 16 bits TC2

Direct II Form,

chebychev, N=3, 16

bits RD

Transoposed Direct

Form II, Chebychev,

N=4, 16 bits TC2

Laticce in state

varibles, Elliptic,

N=4, 16 bits RD

On the other hand it is presented the different

behavior of the performance of each real

implementation of the controller and the impact over

the whole system, so it is important to establish an

analysis of the whole system as in this paper, not

only for the controller.

Due to the reduced time for analyzing these

systems, it seem to be important to introduce this

analysis as a part of the design process for choosing

the correct implementation where working under

fixed-point arithmetic.

A COMPUTER ORIENTED ALGORITHM FOR ANALYZING LIMIT CYCLES IN DISCRETE CONTROL SYSTEMS

159

N T C TIME

SAT 2 0 0 1 1 0,19

OV 7 2 4 8 115 49,781

SAT 3 0 0 9 9 0,561

OV 4 25 2 7 116 67,427

SAT 0 0 0 0 0 0,371

OV 2 23 1 1 115 14,732

SAT 3 3 3 10 3 0,41

OV 5 102 102 4 115 40,538

SAT 4 4 4 1 5 32,01

OV 5 104 104 11 116 77,492

SAT 0 0 0 0 0 0,341

OV 4 103 103 4 116 15,322

SAT53311103 23,914

OV 7 115 115 23 23 7 115 40,669

SAT5551125 124,44

OV 5 116 116 23 23 4 116 53,817

SAT0000000 7,431

OV 2 115 115 22 22 1 115 14,541

SAT 6 0 0 1 0 10 4 3,565

OV 8 13 3 19 2 5 116 329,474

SAT 7 3 1 3 0 15 13 883,591

OV 4 14 4 2 1 7 118 1350,53

SAT0000000 0,371

OV 2 12 3 19 1 4 116 161,663

TC2

TMS

TC2

TMS

TC2

TMS

TC2

TMS

4 CONCLUSIONS

The behaviour of discrete control systems under

finite precision applied to any data to be stored in a

real hardware is dependent on the real hardware

implementation, that is, the real discrete algorithm

stored. Many different implementations have been

early studied and they must be analized under finite

precision to guarantee the good performance in real

implementations. One of the problems under finite

precision are the possible oscillations at the output

and internal registers called limit cycles.

This paper suggests a fast algorithm for the

analysis and characterization of those limit cycles

that appear in any recursive implementation. It has

been shown that presents a less computing time than

exhaustive formulations and produce results more

accurate than theoretical calculations. Besides it is

applicable to any type of implementation and type of

quantization scheme, since it uses the difference

equation system to describe the system.

Therefore it can be used as a part of design

process to select the best real implementation for the

controller when working under fixed-point

arithmetic.

REFERENCES

Table 2: Digital Control System Analysis

Bauer, P.H.; Leclerc, L.-J., Nov. 1991. A Computer-Aided

test for the Absence of Limit Cycles in Fixed-Point

Digital Filters. In ICEIS’99, IEEE Trans. Sig. Proc.,

vol. 39, no. 11, pp. 2400-2409.

Premaratne, K.; Kulasekere, E.C.; Bauer, P.H.; Leclerc,

L.-J., 1995. An Exhaustive Search Algorithm for

Checking Limit Cycle Behavior of Digital Filters.

Proc. IEEE ISCAS, Seattle, pp. 2035-2038.

B.D. Green, L.E. Turner., 1988. New Limit Cycle Bounds

for Digital Filters. In IEEE Trans. Circuits and

System, vol. 35 ,no.4,

S. Yakowitz, S.R. Parker., 1973. Computation of bounds

for digital quantization errors In In IEEE Trans.

Circuit Theory CT.-20 (July 1973) pp. 391-396, pp.

391-396

M. Utrilla Manso, F. López Ferreras; D. Osés-del Campo,

R. Jiménez-Martínez., 2000. A DSP-Oriented Fast

Algorithm to Detect and Characterize Limit Cycles in

Digital Filters. In Problems in Modern Applied

Mathematics ISBN 960-8052-15-7, pp.198-203, Ed.

World Scientific and Engineering Society Press

D. Osés-Del Campo; F.López-Ferreras; M. Utrilla-

Manso;F.Cruz-Roldán., 2000. Fast Algorithms for the

Analysis and Characterisation of Limit Cycles in

Fixed-Point Digital Filters. In Problems in Modern

Applied Mathematics ISBN 960-8052-15-7, pp.187-

191, Ed. World Scientific and Engineering Society

Press.

A. Djebbari, M.F. Belbachir, J.M. Rouvaen., 1998. A fast

exhaustive search algorithm for checking limit cycles

in fixed-point digital filters. In Signal Processing 69,

Elsevier Science pp. 199-205

Franklin, G. F. y Powell J.D., Nov. 1997.. Digital control

of dinamics systems. Addison Wesley

Kat. Ogata., Nov. 1996. Sistemas de Control en Tiempo

Discreto. Pearson Education 2

Ed.

John B. Slaughter, 1963. Quantization Errors in Digital

Control System In IEEE Transactions on Automatic

Control. pp: 69-74..

P.Diniz, E Silva and S. Netto., 2002. Digital Signal

Processing: system and analysis, Cambridge

University Press.

C.L. Phillips, H.T. Nagle, 1990, Digital Control System

Analysis and Design, 2

Ed, Prentice Hall.

A. V. Oppenheim, R. W. Schafer, 1999, Discrete-Time

Signal Processing, 2

Ed, Prentice Hall.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

160