PARAMETER ESTIMATION OF MOVING AVERAGE PROCESSES
USING CUMULANTS AND NONLINEAR OPTIMIZATION
ALGORITHMS
M. Boulouird, M. M. Hassani
Laboratoire d’Electronique et Instrumentation LEI (FSSM/UCAM)
Department of Physics, Faculty of Sciences Semlalia
Avenue Prince My Abdellah, B.P 2390, 40001 Marrakesh, Morocco
G. Favier
Laboratoire d’Informatique, Signaux et Systèmes de Sophia-Antipolis I3S (CNRS/UNSA)
Les algorithmes - Bâtiment Euclide B, 2000 route des Lucioles
B.P 121, Sophia Antipolis Cedex France
Keywords:
MA system identification, Higher-Order Statistics, Estimation parameter, Linear algebra solution, Gradient
descent algorithm, Gauss-Newton algorithm, Cumulants.
Abstract:
In this paper nonlinear optimization algorithms, namely the Gradient descent and the Gauss-Newton algo-
rithms, are proposed for blind identification of MA models. A relationship between third and fourth order
cumulants of the noisy system output and the MA parameters is exploited to build a set of nonlinear equa-
tions that is solved by means of the two nonlinear optimization algorithms above cited. Simulation results are
presented to compare the performance of the proposed algorithms.
1 INTRODUCTION
Numerous methods have been proposed in the lite-
rature for blind identification of MA models using
cumulants. The present paper is concerned with
the linear algebra solutions approach. It consists in
constructing a system of equations obtained from ex-
plicit relations that link third and fourth order cumu-
lants of the noisy output with the MA parameters and
solving this system by the least-squares method ((Al-
shebeili, 1993), (Giannakis, 1989), (Martin, 1996),
(Na, 1995), (Srinivas, 1995), (Stogioglou, 1996), (Tu-
gnait, 1990), (Tugnait, 1991)). In order to take the
redundancy in the unknown parameters vector into
account, (Abderrahim, 2001) proposed a constrained
optimization based solution.
In this paper, we propose another approach to re-
duce this redundancy. It consists in exploiting the non-
linearity existing in the unknown parameters estima-
ted vector. In the literature, the parameters of the vec-
tor to be estimated are regarded as independent, but
actually it isn’t the case. Thus the major contribution
of this paper lies in the estimates of a non redundant
vector of unknown parameters.
The organization of this paper is as follows. The
problem formulation is given in Section 2. In Sec-
tion 3, the resolution with least squares and the non-
linear optimization algorithms, in the event Gradient
descent and Gauss-Newton algorithms, well be deve-
loped. Computer simulation results are given in Sec-
tion 4 to show the effectiveness of the proposed tech-
niques. Finally, the paper is concluded in Section 5.
2 PROBLEM FORMULATION
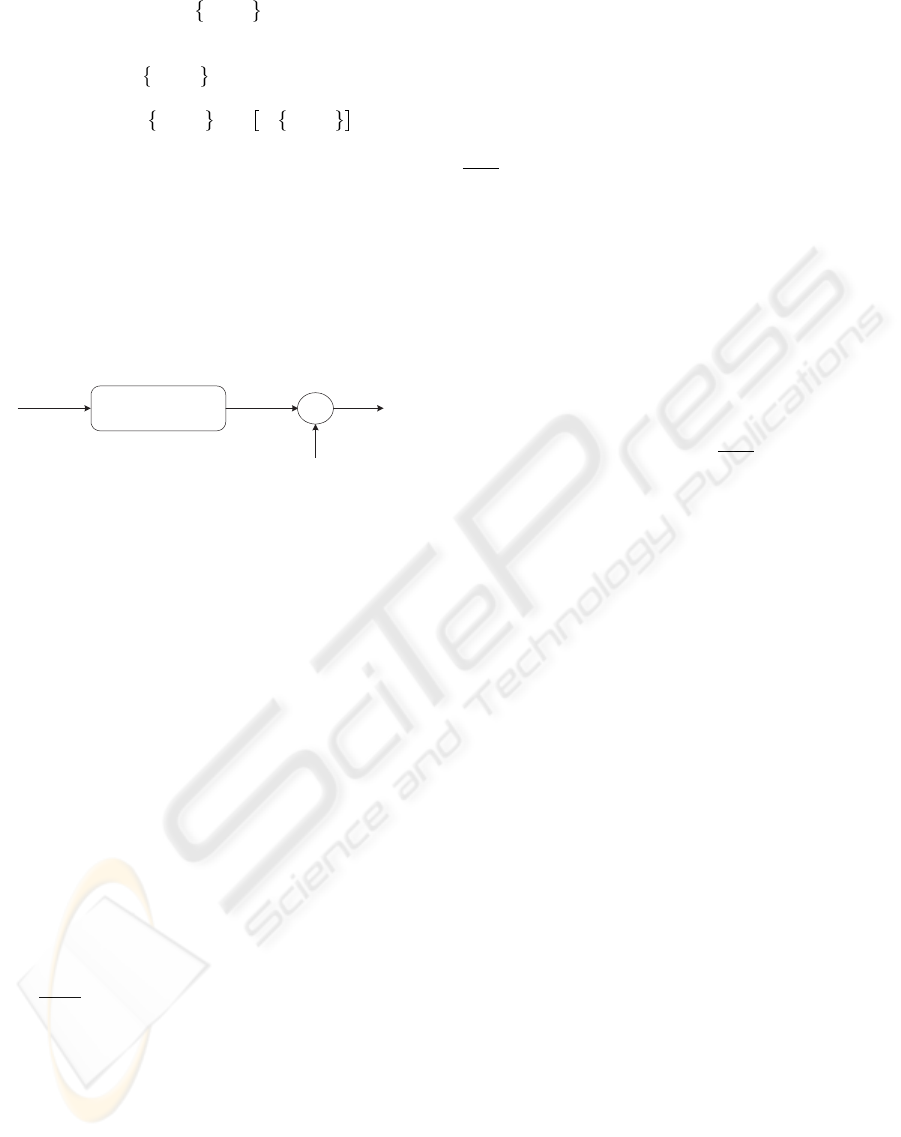
We consider the discrete, causal, linear time-invariant
process represented on figure 1, with the following
assumptions :
H.1. The input w(k) is a zero mean, independent
and identically distributed (i.i.d), stationary non-
Gaussian, non measurable real sequence, with
unknown distribution, and :
C
m,w
(τ
1
, τ
2
, . . . , τ
m−1
) = γ
m,w
δ(τ
1
, τ
2
, . . . , τ
m−1
)
where :
⋄ C
m,w
(τ
1
, τ
2
, . . . , τ
m−1
) is the mth-order cu-
mulant of the input signal of the MA model.
⋄ γ
m,w
6= 0, ∀ m ≥ 2
⋄ γ
m,w
= C
m,w
( 0, 0, . . . , 0
m−1
)
11
Boulouird M., M. Hassani M. and Favier G. (2005).
PARAMETER ESTIMATION OF MOVING AVERAGE PROCESSES USING CUMULANTS AND NONLINEAR OPTIMIZATION ALGORITHMS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 11-15
DOI: 10.5220/0001182900110015
Copyright
c
 SciTePress

⋄ γ
2,w
= σ
2
w
= E
w(k)
2
is the variance of
w(k).
⋄ γ
3,w
= E
w(k)
3
is the skewness of w (k).
⋄ γ
4,w
= E w(k)
4
− 3 E w(k)
2
2
is the
kurtosis of w(k).
H.2. The additive noise v(k) is assumed to be an
i.i.d Gaussian sequence with unknown variance,
zero-mean, and independent of w (k).
H.3. The non measurable output x(k) is assumed
to be a nonminimum or minimum phase MA
process.
H.4. The order q of the model is assumed to be
known.
w(k)
H(z)
+
x(k)
v(k)
y(k)
Figure 1: Single-channel system.
The measured noisy MA process y(k) is represen-
ted by the following equations :
x(k) =
q
X
i=0
h(i) w(k − i); {h(0) = 1} (1)
y(k) = x(k) + v(k) (2)
For the MA model described by equation (1) with
the assumptions H.1, H.2, H.3, and H.4, the mth and
nth-order cumulants of the MA system output (2) are
linked by the following relation (Abderrahim, 2001) :
i
max
X
i=i
min
h(i)
"
m−s−1
Y
k=1
h(i + τ
k
)
#
×
C
n,y
(β
1
, β
2
, . . . , β
n−s−1
, i+α
1
, i+α
2
, . . . , i+α
s
) =
γ
n,w
γ
m,w
j
max
X
j=j
min
h(j)
"
n−s−1
Y
k=1
h(j + β
k
)
#
×
C
m,y
(τ
1
, τ
2
, . . . , τ
m−s−1
, j+α
1
, j+α
2
, . . . , j+α
s
)
(3)
where m > 2, n > 2 and s is an arbitrary integer
number satisfying : 1 ≤ s ≤ min(m, n) − 2,
and





i
min
= max(0, −τ
1
, · · · , −τ
m−s−1
)
i
max
= min(q, q − τ
1
, · · · , q − τ
m−s−1
)
j
min
= max(0, −β
1
, · · · , −β
n−s−1
)
j
max
= min(q, q − β
1
, · · · , q − β
n−s−1
)
Setting n = 3, m = 4, and s = 1 in equation (3),
yields
i
max
X
i=i
min
h(i)h(i + τ
1
)h(i + τ
2
)C
3,y
(β
1
, i + α
1
) =
γ
3,w
γ
4,w
j
max
X
j=j
min
h(j)h(j + β
1
)C
4,y
(τ
1
, τ
2
, j + α
1
) (4)
where





i
min
= max(0, −τ
1
, −τ
2
)
i
max
= min(q, q − τ
1
, q − τ
2
)
j
min
= max(0, −β
1
)
j
max
= min(q, q − β
1
)
By setting τ
1
= τ
2
= 0 in (4), we get the rela-
tion used in this paper for estimating the parameters
{h(i)}
i=1,2,...,q
of the MA model.
q
X
i=0
h
3
(i)C
3,y
(β
1
, i + α
1
) =
γ
3,w
γ
4,w
j
max
X
j=j
min
h(j)h(j + β
1
)C
4,y
(0, 0, j + α
1
) (5)
It is important to determine the range of
values of α
1
and β
1
so that the cumulants
{C
3,y
(β
1
, i + α
1
)}
i=0,··· ,q
, {C
4,y
(0, 0, j +
α
1
)}
j=j
min
,··· ,j
max
, and the coefficients {h(j + β
1
)}
be not all zero for each equation.
By taking account of the property of causality of
the model and the domain of support for third and
fourth order cumulants of an MA(q) process (Mendel,
1991), we obtain :





−q ≤ β
1
≤ q
−2q ≤ α
1
≤ q
−2q + β
1
≤ α
1
≤ q + β
1
(6)
Using the symmetry properties of cumulants (Ni-
kias, 1993), the set of values for α
1
and β
1
is defined
by :
(
−q ≤ β
1
≤ 0
−2q ≤ α
1
≤ q + β
1
(7)
3 PARAMETER ESTIMATION
3.1 Least-Squares (LS) Solution
Concatenating (5) for all values of α
1
and β
1
defined
by (7), we obtain the following system of equations :
Mθ = r (8)
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
12

where :
θ = [h(1) · · · h(q) h
2
(1) h(1)h(2)
· · · h(1)h(q) h
2
(2) · · · h(2)h(q) h
2
(3)
· · · h
2
(q) ǫ
4,3
ǫ
4,3
h
3
(1) · · · ǫ
4,3
h
3
(q)]
T
(9)
⋄ ǫ
4,3
= γ
4,w
/γ
3,w
.
⋄ M is a matrix of dimension
5q
2
+7q+2
2
,
q
2
+5q+2
2
.
⋄ θ is a vector of dimension
q
2
+5q+2
2
, 1
.
⋄ r is a vector of dimension
5q
2
+7q+2
2
, 1
.
Assuming that (M
T
M) is invertible, the unique LS
estimate of θ is
ˆ
θ = (M
T
M)
−1
M
T
r (10)
Solving (8) provides the parameter estimates
{h(i)}
i=1,··· ,q
as the first q components of the
estimated parameter vector
ˆ
θ in (10).
3.2 Gradient Descent Algorithm
(GDA)
The idea satisfying this paper is to reduce the dimen-
sion of the estimated parameter vector (9). In section
3.1, θ is a vector of
q
2
+5q+2
2
elements. The linear
algebra solutions regard the elements of the vector θ
clarified in relation (9) as independent parameters, but
the dependence of these elements is almost obvious.
To palliate the problem of redundancy in θ, we pro-
pose a new approach based on non-linear optimiza-
tion algorithm. In this part, the parameters vector θ is
a (q + 1) length vector. It has this form :
θ
NL
= [h(1), · · · , h(q), ǫ
4,3
]
T
(11)
The criterion to be minimized in this case is as fol-
lows :
J
LS
= kr − φ(θ
NL
)k
2
The GDA solution has the following form :
ˆ
θ
i+1
NL
gr
=
ˆ
θ
i
NL
gr
+ λJ
T
(r − φ(
ˆ
θ
i
NL
gr
)) (12)
where :
⋄ r is defined in section 3.1.
⋄ φ is the system of equations obtained by conca-
tenating (5) for all values of α
1
and β
1
defined
by (7).
⋄ J is the Jacobian matrix of φ,
J =

∂φ
k
∂θ
NL
l

(k,l)
where k = 1, · · · ,
5q
2
+7q+2
2
, and l = 1, · · · , q+1.
⋄ λ is the step-size.
The parameter ǫ
4,3
must be estimated since we are
supposed that we don’t know the nature of the distri-
bution of the input signal w(k).
3.3 Gauss-Newton Algorithm (GNA)
This algorithm has this form :
ˆ
θ
i+1
NL
gn
=
ˆ
θ
i
NL
gn
+ µ(J
T
J)
−1
J
T
(r − φ(
ˆ
θ
i
NL
gn
))
(13)
where :
⋄ r, φ, and J are defined in section 3.2.
⋄
ˆ
θ
NL
gn
has the form of (11).
⋄ µ is the step-size of this algorithm.
4 SIMULATION RESULTS
To demonstrate the effectiveness of the proposed
techniques, let us examine two examples treated in
the literature. In both models the input signal w(k) is
a zero-mean exponentially distributed i.i.d noise se-
quence with γ
2,w
= σ
2
w
= 1 and γ
3,w
= 2. We define
the Signal-to- Noise Ratio as
SN R(dB) = 10 log
10

E[x
2
(k)]/E[v
2
(k)]

For each run, we calculate the Normalized Mean
Square Error (NMSE) defined as
NMSE =
P
q
i=1

h(i) −
b
h(i)

2
P
q
i=1
h
2
(i)
where h(i) and
b
h(i) are respectively the actual and the
estimated impulse responses, respectively. The Error
to Signal Ratio (ESR) in decibels is also used as a
measure of the estimation error. The ESR is defined
as
ESR(dB) = 10 log
10
(NMSE)
Example 1 :
y(k) = w(k)−2.3333w(k−1)+0.6667w(k−2)+v(k)
The zeros of the system transfer function H(z) are lo-
cated at 2 and 0.3333. This model has also been used
in (Abderrahim, 2001), (Giannakis, 1989), and (Srini-
vas, 1995).
Additive colored noise is generated as the output of
the following MA(2) model (Abderrahim, 2001) :
v(k) = e(k) + 2.3333e(k − 1) − 0.6667e(k − 2)
where the input sequence e(k) is an i.i.d Gaussian
sequence. We carried out Monte Carlo simulations
with K = 100 different noise sequences, N = 5120
data for each run, and three different values of SNR
(20dB, 10dB, and 0dB). The simulation results are
summarized in Tables 1, 2, and 3.
Example 2 :
y(k) = w(k) + 0.1w (k − 1) − 1.87w(k − 2)
+3.02w(k−3)−1.435w(k−4)+0.49w(k−5)+v(k)
PARAMETER ESTIMATION OF MOVING AVERAGE PROCESSES USING CUMULANTS AND NONLINEAR
OPTIMIZATION ALGORITHMS
13

Table 1: System identification using signal model MA(2),
Mean, Standard deviation, NMSE, and ESR . SNR=20dB.
True Values LS GDA GNA
λ = 8. 10
−5
µ = 0.5
h(1) -2.3333 mean -2.1704 -2.2676 -2.2676
σ 0.0585 0.0149 0.0149
h(2) 0.6667 mean 0.5101 0.6541 0.6541
σ 0.0211 0.0060 0.0060
NMSE mean 0.0093 0.0008 0.0008
σ 0.0043 0.0003 0.0003
ESR -20.3041 -30.9500 -30.9500
Table 2: System identification using signal model MA(2),
Mean, Standard Deviation, NMSE, and ESR. SNR=10dB.
True Values LS GDA GNA
λ = 8. 10
−5
µ = 0.5
h(1) -2.3333 mean -2.1013 -2.1158 -2.2624
σ 0.1835 0.4664 0.0511
h(2) 0.6667 mean 0.4987 0.6166 0.6557
σ 0.0632 0.1275 0.0192
NMSE mean 0.0203 0.0478 0.0014
σ 0.0181 0.1490 0.0015
ESR -16.9250 -13.2057 -28.5387
The zeros of the system transfer function H(z) are lo-
cated at −2, 0.7±j0.7 and 0.25±j0.433. This model
has also been used in (Alshebeili, 1993), (Stogioglou,
1996), (Tugnait, 1990), and (Tugnait, 1991).
Additive colored noise is generated as the output of
the following MA(3) model (Abderrahim, 2001) and
(Na, 1995) :
v(k) = e(k)+0.5e(k−1)−0.25e(k−2)+0.5e(k−3)
where the input sequence e(k) is an i.i.d Gaussian se-
quence. In this case N = 10240. The simulation re-
sults are given in tables 4, 5, and 6.
In these simulations, we initialize the nonlinear op-
timization algorithms with the LS solution. The ad-
vantage of this is to avoid the convergence to local
minimum. The good value of the step-size allows also
to avoid this problem of the local minima.
Table 1 shows that the parameters estimation via
the proposed method is much more powerful than LS
solution in term of mean value, standard deviation, or
NMSE, and ESR . The Gradient Descent and Gauss-
Newton algorithms converge to the same values, but
the convergence speed is different. The figures 2 and
3 illustrate this.
Tables 2 and 5 show that the Gradient Descent al-
gorithm is sensitive to the additive noise. However,
the Gauss-Newton algorithm is more robust to mea-
surement noise.
We can note that for a low SNR (SNR = 0dB),
the estimate of the parameters is poor what is due
to the bad estimate of third and fourth order cumu-
lants. These estimation results could be improved by
processing more data, which allows to get better esti-
mates of the cumulants.
Table 3: System identification using signal model MA(2),
Mean, Standard Deviation, NMSE, and ESR. SNR=0dB.
True Values LS GDA GNA
λ = 8. 10
−5
µ = 0.5
h(1) -2.3333 mean -1.3781 -0.8631 -1.0952
σ 0.6033 0.6223 1.0662
h(2) 0.6667 mean 0.3217 0.3006 0.2882
σ 0.1794 0.2092 0.3499
NMSE mean 0.2418 0.4623 0.4964
σ 0.2464 0.2762 0.4890
ESR -6.1661 -3.3511 -3.0421
Table 4: System identification using signal model MA(5),
Mean, Standard Deviation, NMSE, and ESR. SNR=20dB.
True Values LS GDA GNA
λ = 6. 10
−9
µ = 0.5
h(1) 0.1 mean 0.0474 0.0779 0.0887
σ 0.0359 0.0384 0.0392
h(2) -1.87 mean -1.4212 -1.2822 -1.7798
σ 0.0845 0.0665 0.1010
h(3) 3.02 mean 2.2489 1.6874 2.8902
σ 0.1258 0.0667 0.1494
h(4) -1.435 mean -1.0779 -1.1768 -1.4206
σ 0.0671 0.0754 0.0876
h(5) 0.49 mean 0.3640 0.3927 0.4536
σ 0.0275 0.0301 0.0320
NMSE mean 0.0651 0.1484 0.0046
σ 0.0221 0.0184 0.0075
ESR -11.8660 -8.2867 -23.3527
By increasing the order q of the model, we use the
third and fourth order cumulants with large lags that
are poorly estimated for a low SNR. The consequence
of this is the bad parameters estimated (table 6) much
poorer than in the case of a model of order 2 (table 3).
These two algorithms are numerically expensive
compared to the Least-Squares algorithm.
5 CONCLUSION
In this paper, a blind identification of the MA mo-
dels using Higher-Order Statistics (HOS) is exposed.
The linear algebra solution is compared with the non-
linear optimization algorithms solution. Computer si-
mulation results prove that it is interesting to use this
algorithms in spite of their expensive calculative cost.
REFERENCES
Abderrahim, K., Ben Abdennour, R., Favier, G., Ksouri, M.,
and Msahli, F. (2001). New Results on FIR Identifica-
tion using Cumulants. Journal Européen des Systèmes
Automatisés-JESA, Vol. 35, No. 5, pp. 601-622.
Alshebeili, S. A., Venetsanopoulos, A. N., and Cetin, A.
E. (1993, April). Cumulant Based Identification Ap-
proaches for Nonminimum Phase FIR Systems. IEEE
Transactions on Signal Processing, Vol. 41, No. 4, pp.
1576-1588.
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
14

Giannakis, G. B., and Mendel, J. M. (1989, March). Iden-
tification of Nonminimum Phase Systems Using Hi-
gher Order Statistics. IEEE Transactions on Acous-
tics, Speech, and Signal Processing, Vol. 37, No. 3,
pp. 360-377.
Martin, J. K., and Nandi, A. K. (1996, January). Blind Sys-
tem Identification using Second, Third and Fourth Or-
der Cumulants. Journal of the Franklin Institute : En-
ginnering and applied mathematics, Pergamon, Vol.
333(B), No. 1, pp. 1-13.
Mendel, J. M. (1991, March). Tutorial on Higher-Order
Statistics (Spectra) in Signal Processing and System
Theory : Theoretical Results and some Applications.
Proceedings of the IEEE, Vol. 79, No. 3, pp. 278-305.
Na, Y. N., Kim, K. S., Song, I., and Kim, T. (1995, Decem-
ber). Identification of Nonminimum Phase FIR Sys-
tems Using the Third- and Fourth-Order Cumulants.
IEEE Transactions on Signal Processing, Vol. 43, No.
8, pp. 2018-2022.
Nikias, C. L., and Mendel, J. M. (1993, July). Signal Pro-
cessing With Higher Order Spectra. IEEE Signal Pro-
cessing Magazine, pp. 10-37.
Srinivas, L., and Hari, K. V. S. (1995, December). FIR Sys-
tem Identification Using Higher Order Cumulants - A
Generalized Approach. IEEE Transactions on Signal
Processing, Vol. 43, No. 12, pp. 3061-3065.
Stogioglou, A. G., and McLaughlin, S. (1996, July). MA
Parameter Estimation and Cumulant Enhancement.
IEEE Transactions on Signal Processing, Vol. 44, No.
7, pp. 1704-1718.
Tugnait, J. K. (1990, July). Approaches to FIR System Iden-
tification With Noisy Data Using Higher Order Statis-
tics. IEEE Transactions on Signal Processing, Vol. 38,
No. 7, pp. 1307-1317.
Tugnait, J. K. (1991, October). New Results on FIR System
Identification Using Higher-Order Statistics. IEEE
Transactions on Signal Processing, Vol. 39, No. 10,
pp. 2216-2221.
Table 5: System identification using signal model MA(5),
Mean, Standard Deviation, NMSE, and ESR. SNR=10dB.
True Values LS GDA GNA
λ = 6. 10
−9
µ = 0.5
h(1) 0.1 mean -0.0929 -0.0841 -0.0604
σ 0.1145 0.1193 0.1161
h(2) -1.87 mean -1.0274 -0.9433 -1.2443
σ 0.2466 0.2177 0.3461
h(3) 3.02 mean 1.6917 1.4036 2.1096
σ 0.3516 0.2240 0.5103
h(4) -1.435 mean -0.8187 -0.8680 -0.9787
σ 0.1748 0.1971 0.2740
h(5) 0.49 mean 0.2760 0.2902 0.3151
σ 0.0653 0.0692 0.0887
NMSE mean 0.2122 0.2694 0.1311
σ 0.1105 0.0959 0.1345
ESR -6.7328 -5.6965 -8.8246
Table 6: System identification using signal model MA(5),
Mean, Standard Deviation, NMSE, ESR. SNR=0dB.
True Values LS GDA GNA
λ = 6. 10
−9
µ = 0.5
h(1) 0.1 mean -0.2698 -0.2888 -0.3315
σ 0.1083 0.1154 0.1085
h(2) -1.87 mean -0.1297 -0.1187 -0.0863
σ 0.1577 0.1459 0.0811
h(3) 3.02 mean 0.3457 0.3302 0.2627
σ 0.2129 0.2021 0.1582
h(4) -1.435 mean -0.1644 -0.1630 -0.0949
σ 0.1068 0.1061 0.0845
h(5) 0.49 mean 0.0420 0.0427 0.0237
σ 0.0366 0.0359 0.0321
NMSE mean 0.8191 0.8280 0.8732
σ 0.1353 0.1300 0.0936
ESR -0.8667 -0.8199 -0.5887
0 10 20 30 40 50 60
−2.3
−2.28
−2.26
−2.24
−2.22
−2.2
Gradient descent algorithm − h(1)=−2.3333 (True value of h(1))
0 10 20 30 40 50 60
−2.27
−2.26
−2.25
−2.24
−2.23
−2.22
−2.21
−2.2
Gauss−Newton algorithm − h(1)=−2.3333 (True value of h(1))
Estimated parameter h(1)
Figure 2: The convergence of h(1).
0 10 20 30 40 50 60
0.64
0.65
0.66
0.67
0.68
0.69
0.7
Gradient descent algorithm − h(2)=0.6667 (True value of h(2))
0 10 20 30 40 50 60
0.56
0.58
0.6
0.62
0.64
0.66
Gauss−Newton algorithm − h(2)=0.6667 (True value of h(2))
Estimated parameter h(2)
Figure 3: The convergence of h(2).
PARAMETER ESTIMATION OF MOVING AVERAGE PROCESSES USING CUMULANTS AND NONLINEAR
OPTIMIZATION ALGORITHMS
15