HYBRID ALGORITHMS FOR THE PARAMETER ESTIMATE
USING FAULT DETECTION, AND REACHING CAPACITIES
Ryadh H. Mokhneche, Hichem Maaref and Vincent Vigneron
Laboratoire Syst
`
emes Complexes
Universit
´
e d’Evry - CNRS FRE2494
40 rue du Pelvoux 91020 Evry, France
Keywords:
Estimation, Detection, Compensation, non-stationary system.
Abstract:
The nonstationary systems parametric estimate requires the continuation of its parameters which vary abruptly
at unknown random moments. These are the abrupt parametric variations which were considered in this work
to be managed like ”faults”. The considered signals here are nonstationary and are characterized by time
variable parameters. The estimate of these parameters requires the choice of an algorithm having the capacity
to continue their evolution. The various hybrid adaptive estimate methods showed that these capacities can be
reached by a compensation of a gain and its update in online. In this paper, a method of estimate is proposed,
based on the fault detection. The general algorithm implemented gives place to several methods which will
be detailed. Experimental tests of some methods on a second order autoregressive synthesis signal are carried
out and then commented.
1 INTRODUCTION
For several years, the fault detection, or abrupt
changes of one or several parameters, has given place
to many work (Frank, 1996) in very varied applica-
bility like the dynamic systems control (J. Ragot and
Ribbens, 1993), the defects or breakdowns detection
of the controlled systems (Wagner and Shoureshi,
1992; Magaldi, 1997), the biomedical diagnosis
(Corge and Puech, 1986), the speech proc-essing for
the recognition and the image processing (Basseville,
1982) and the signal adaptive processing (A. Kobi
and Ragot, 1994). In this work, one is interested to
the nonstationary systems parametric estimate char-
acterized by time variable parameters which presents
abrupt variations regarded here as faults, and whose
estimate requires an algorithm able to follow their
evolution (Macchi and Turki, 1992).
It is presented a complete procedure of a method
combining the adaptive methods and the fault detec-
tion for nonstationary signals. A general algorithm
of parametric estimate is established, giving place to
several under-algorithms. Experimental tests are car-
ried out on a second order autoregressive synthesis
signal, noted AR2.
2 HYBRID ADAPTIVE ESTIMATE
METHODS
These methods show that it is possible to approach the
real parameters by a compensation Ω of the gain P , in
its update which we describe in his hybrid form (1):
ρP (t) = −
¯
P (t) + Ω (t)
¯
P (t)
∆
=
α(t)P (t)ϕ(t)ϕ
T
(t)P (t)
Γ(t)+T
e
ϕ
T
(t)P (t)ϕ(t)
(1)
where α(t) is a positive weight function ∀t and Γ(t) a
standardization term > 0. Ω(t) is an update function,
of the gain P (t), representing the covariance estimate
of the parametric variations. T
e
is the sampling pe-
riod.
The choice of Ω(t) and of the compensation pro-
cedure define the hybrid adaptive estimate method
(HAEM) considered. One can group the various
HAEM in 2 kinds:
• The HAEM with ”continue” compensation of
gain:
Ω (t)
∆
= function of time t. The compensation of
gain is done with each iteration; it is the case of
methods with forgetting factor.
289
H. Mokhneche R., Maaref H. and Vigneron V. (2005).
HYBRID ALGORITHMS FOR THE PARAMETER ESTIMATE USING FAULT DETECTION, AND REACHING CAPACITIES.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 289-293
DOI: 10.5220/0001183202890293
Copyright
c
 SciTePress

• The HAEM with compensation of gain after de-
tection of fault (2):
Ω (t)
∆
= Ω
0
(t) δ (t − t
r
)
=⇒

Ω (t) = 0 if t 6= t
r
Ω (t) = Ω
0
(t) if t = t
r
(2)
where Ω
0
(t) is the amplitude of the update fonction
Ω(t), t
r
the fault moment, and δ(t − t
r
) the Dirac
impulse at moment t − t
r
. Ω
0
(t
r
) is the compensa-
tion term who expresses himself either according to
the Fisher Information matrix (FIM), or according
to the covariance matrix (CovMat). Its expression
is carried out in the q
−1
recursive case and the δ
recursive case.
3 HYBRID ADAPTIVE
PARAMETRIC ESTIMATE BY
FAULT DETECTION
The principle is: as soon as a fault is detected, it is
necessary to act immediately on the estimate algo-
rithm to correct the adaptation gain and to enable him
to compensate the fault while choosing well Ω
0
(t).
This gives place to several methods whose essential
idea is to couple an estimate algorithm with a fault
detection algorithm.
Figure 1: Principle of the hybrid adaptive parametric esti-
mate controlled by fault detection.
The procedure suggested uses as criterion the Re-
cursive Least Squares (RLS) (Goodwin and Middle-
ton, 1990). The algorithm is built in manner that with
each step, a detector tests fault information by carry-
ing out an hypothesis test based either on a confidence
interval (Bendat and Piersol, 1999), or on the proba-
bility ratio (Tanaka and Muller, 1990). The use of
a confidence interval makes it possible to decide the
existence of a fault whatever the adopted model (AR
1
or ARMA
2
). The detector has the capacity to decide
to rectify the consequently algorithm according to the
diagram of the figure (1).
Table 1: The alternatives of the HAEM by fault detection.
Detection test operator Compensation
χ
2
derivative δ FIM or CovMat
χ
2
delay q
−1
FIM or CovMat
Fisher derivative δ FIM or CovMat
Fisher delay q
−1
FIM or CovMat
Student derivative δ FIM or CovMat
Student delay q
−1
FIM or CovMat
RDPR derivative δ FIM or CovMat
RDPR delay q
−1
FIM or CovMat
The algorithm proposed is structured as follows:
on a basis kind MCR are grafted three successive
phases which are the construction of an Information
Signal IS, the test of fault detection and the com-
pensation of the detected fault. According to the
choice of the nature of each one of these 3 phases, it
was elaborate several alternatives of the method thus
giving place to eight different tests for an operator
given (q or δ) which are grouped in table (1).
The detection tests apply to the signal IS and are
based on the Probability Ratio PR (test built on the re-
cursive deviation of the PR and called RDPR) and/or
the interval confidence built using the distributions χ
2
or Fisher or Student. The compensation procedure is
carried out in an indirect way: the adaptation gain is
corrected in real time by the intermediary of a func-
tion either of the Fisher Information Matrix (FIM) or
of the Covariance Matrix of the parametric drift (Cov-
Mat) (Tab. 1).
3.1 The global hybrid algorithm
The global algorithm of the whole of the HAEM
by fault detection methods proposed in figure (1)
is based on the equations (3) and (4), and corre-
sponding to equations (5-12) of table (2) for the case
α (t) = Γ (t) = 1.
ρ
ˆ
θ (t) =
α (t) P (t) ϕ (t)
h
y (t) − ϕ
T
(t)
ˆ
θ (t)
i
Γ (t) + T
e
ϕ
T
(t) P (t) ϕ (t)
(3)
1
Auto-Regressif
2
Auto-regressif with Adjusted Mean
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
290

ρP (t) = −
α (t) P (t) ϕ (t) ϕ
T
(t) P (t)
Γ (t) + T
e
ϕ
T
(t) P (t) ϕ (t)
+Ω(t) (4)
where α (t) ∈ [0, 1] is a positive weight function
(∀t), Γ(t) is the standardization term (> 0) and Ω(t)
the update function covariance matrix or adaptation
gain P (t) such as Ω(t) = Ω
T
(t) ≥ 0.
Table 2: Hybrid algorithm
the parameter vector:
θ (t) =

a
1
(t) , · · · , a
n
(t) ,
b
1
(t) , · · · , b
n
(t)

T
(5)
the measure vector:
ϕ (t) =

−ρ
n−1
y (t) , · · · , −ρy (t) ,
ρ
m
u (t) , · · · , u (t)]
T
(6)
ρ
ˆ
θ (t) =
P (t)ϕ(t)ε(t)
1+T
e
ϕ
T
(t)P (t)ϕ(t)
(7)
ρP (t) = −
¯
P (t) + Ω (t) (8)
¯
P (t)
∆
=
P (t)ϕ(t)ϕ
T
(t)P (t)
1+T
e
ϕ
T
(t)P (t)ϕ(t)
(9)
Ω (t) = Ω
0
(t) δ (t − t
r
) (10)
with the estimated parameter vector:
ˆ
θ (t) =

ˆa
1
(t) , · · · , ˆa
n
(t) ,
ˆ
b
1
(t) , · · · ,
ˆ
b
n
(t)

T
(11)
P (t) is the adaptation gain,
T
e
is the sampling period
and t
r
is the fault moment.
Ω
0
(t) is the update function of the gain.
The prediciton error is such as:
ε (t) = y (t) − ϕ
T
(t)
ˆ
θ (t) (12)
4 EXPERIMENTAL TESTS AND
RESULTS
Some various algorithms of table (1) were applied to
a 2nd order autoregressive synthesis test signal noted
AR2, and their performances were tested on this sig-
nal.
4.1 Construction of the test signal
The AR2 test signal built is given by the figure (2a),
and it is fed by a generating white noise η(t) (figure
2c). The variations of the two parameters a
1
and a
2
are represented on the figure (2b). The figure (2d)
shows the AR2 spectral density.
Figure 2: Construction of the AR2 Signal test.
4.2 Application of the algorithms
The estimate algorithms by fault detection (F isher
and Student), the simple RLS algorithm and the RLS
algorithm with constant forgetting factor, for the de-
lay operator q
−1
(Tab. 1), were applied to AR2 test
signal in order to obtain the estimate of the parame-
ters a
1
(k) and a
2
(k).
4.2.1 simple RLS algorithm
The figures (3a) and (3b) shows the estimate of the
parameters a
1
(k) and a
2
(k).
The natural decrease of the adaptation gain of the
parameter a
2
(figure 3f) can be noticed, where the es-
timate error is very important.
The simple RLS algorithm can not follow the para-
meter variations.
4.2.2 RLS algorithm with constant forgetting
factor
The figures (3c) and (3d) gives the results of the esti-
mate.
The estimate approaches the true value, the gain
(figure 3e) is maintained sufficiently to follow the
parametric variations.
HYBRID ALGORITHMS FOR THE PARAMETER ESTIMATE USING FAULT DETECTION, AND REACHING
CAPACITIES
291

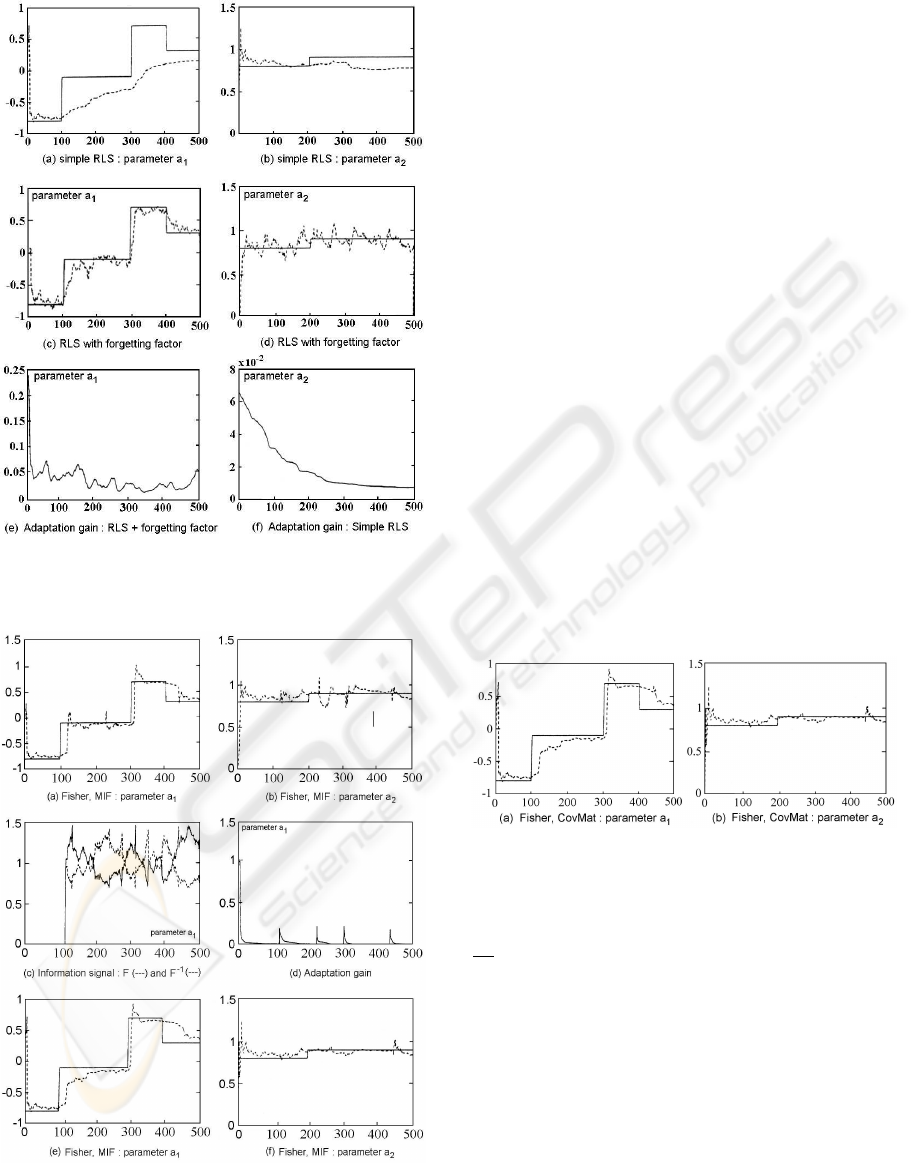
Figure 3: Parametric estimate by the RLS method.
Figure 4: Parametric estimate with fault detection: Fisher
test with FIM.
4.2.3 Fisher test - Fisher detection algorithm and
FIM compensation
With as information signal the prediction gain and its
reverse, the figures (4a) and (4b) gives the estimates.
The figure (4c) shows the confidence interval for
the Fisher test and its reverse, and the figure (4d)
shows the adaptation gain. The detected fault are:
t
r
i
= 120, 228, 306 et 436.
The influence of the window size is visible by
looking at the figures (4a) and (4e) jointly for the
parameter a
1
and the figures (4b) and (4f)) jointly for
the parameter a
2
, for nb
1
= 60 and nb
2
= 120.
4.2.4 Fisher test - Fisher detection algorithm and
CovMat compensation
With the used data information below :
• information signal: the prediction gain and its re-
verse,
• window widths: nb
1
= 80 and nb
2
= 100,
• confidence interval: 90%,
• s
0
= 0.01,
• temporization: t
p
= 40,
Figure 5: Parametric estimate with fault detection: Fisher
test with CovMat.
and for a compensation by the covariance matrix of
∆
ˆ
θ
ˆ
θ
, the obtained results are shown on the figures (5a)
and (5b); one obtains a very good estimate in spite of
false alarm and the light delay.
The estimated fault moments are t
r
i
= 120, 264,
308 et 440.
4.2.5 Student test with FIM/CovMat
compensation
The figures (6a) and (6b) shows the estimated ob-
tained by the FIM compensation and the figures (6c)
and (6d) by the CovMat compensation.
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
292

Figure 6: Parametric estimate with fault detection: Student
test.
5 CONCLUSION
It was shown that the fault detection algorithms pro-
vide estimated which follow very well the fault and
convergent in spite of the fact that some algorithms
give false alarm or nondetections. The elaborate algo-
rithms were applied to nonstationary test signals with
different choices of signal information for the detec-
tion test. This variety of application will give results
which illustrate and make it possible to highlight sev-
eral properties of the nonstationary signal processing
by fault detection for the q
−1
operator. It was shown
also that the statistical tests χ
2
, Fisher and Student
can be applied to detect nonstationnarities of the test
signals. Associated to an estimate and compensation
algorithm, these tests make it possible to follow non-
stationnarities, even brutal, and to increase the perfor-
mances of the algorithm by reducing the skew of the
estimate and by increasing their capacity of continua-
tion. The number of the selected information signals
(FIM, CovMat) will increase the number of alterna-
tives of the hybrid adaptive estimate method by fault
detection suggested, that is to say higher than 8 al-
ternatives. An establishment of all these alternatives
would give an overall assessment, therefore to know
the good method carrying out one better estimate. A
comparative study between the application of the q
−1
algorithms and δ algortithms would be interesting to
deduce the methods ensuring a good estimate and a
better capacity of continuation.
REFERENCES
A. Kobi, S. N. and Ragot, J. (1994). Fault detection iso-
lation and control reconfiguration. 2nd International
Symposium on Mathematical and Intelligent Models
in System Simulation. IMACS, 37:111–117.
Basseville, M. (1982). Sequential detection of abrupt
changes in spectral characteristics of digital signals.
IEEE Symposium on Information Theory - ISIT’82,
pages 21–25.
Bendat, J. S. and Piersol, A. G. (1999). Random data analy-
sis and measurement procedures. John Wiley Sons
Inc., New york.
Corge and Puech (1986). cardiac rate analysis by fault de-
tection methods (in french). Proceedings INRIA, 7th
ICAOS Antibes 1986, France.
Frank, P. M. (1996). Analytical and qualitative model-based
fault diagnosis - a survey and some new results. Euro-
pean Journal of Control, 2(1):6–23.
Goodwin, G. C. and Middleton, R. H. (1990). Digital con-
trol and estimation. a unified approach. Prentice Hall,
New York.
J. Ragot, D. M. and Ribbens, W. B. (1993). Two approaches
for the isolation of plant railures in dynamic systems.
International Conference on fuit diagnosis, Tooldiag
Toulouse, 3:24–28.
Macchi, O. and Turki, M. (1992). The nonstationary de-
gree: can an adaptive filter be worse than no process-
ing. journal of the International Federation of Ac-
countants IFAC - ACASP 92, 1:48–63.
Magaldi, R. (1997). Dealing with the failure in the real
world: a human factors engineering approach. Pro-
ceedings of the Second International Conference on
Case-Based Reasoning Research and Development,
1266:114–121.
Tanaka, S. and Muller, P. C. (1990). Fault detection in linear
discrete dynamic systems by a pattern recognition of
a generalized l.r. Journal of Dynamic Systems, Mea-
surements and Control. Transactions on ASME, 112.
Wagner, J. and Shoureshi, R. (1992). Failure detection diag-
nostics for thermofluid systems. Journal of Dynamic
Systems, Measurement and Control. Transactions on
ASME, 114:699–706.
HYBRID ALGORITHMS FOR THE PARAMETER ESTIMATE USING FAULT DETECTION, AND REACHING
CAPACITIES
293