MODELING AND CONTROLLER DESIGN OF A MAGNETIC

LEVITATION SYSTEM WITH FIVE DEGREES OF FREEDOM

E. Alvarez-Sanchez, Ja. Alvarez-Gallegos and R. Castro-Linares

CINVESTAV-IPN, Department of Electrical Engineering

Av. IPN No. 2508, Col. San Pedro Zacatenco

07360 Mexico, D.F., Mexico

Keywords:

Nonlinear system, modeling, control, maglev.

Abstract:

In this paper, the nonlinear mathematical model with ﬁve DOFs (degrees-of-freedom) of a magnetic levitation

system is developed and analyzed. Then a second order sliding mode controller is proposed to regulate the

levitation to a desired position, stabilizethe other 4 DOFs in the nonlinear system and compensate the unknown

increments on the load. Simulation results are presented to show the effectiveness of the proposed controller.

1 INTRODUCTION

The transport of material or products is a major prob-

lem in the manufacturing automation industry. As

it currently stands transport speciﬁcations can be so

variable from process within a single plant that each

operation might require its own transport. Using mag-

netic levitation (maglev), a carrier can be partially or

totally levitated or suspended by magnetic ﬁelds gen-

erated along the guiding tracks. This allows the car-

rier to move with little or no contact to the guiding

tracks, thus greatly minimizing the problems of en-

vironmental contamination. Of course, such contact-

free levitation has to be enforced for all DOFs of the

rigid body.

Maglev systems offer many advantages such as

frictionless, low noise, the ability to operate in high

vacuum environments and so on. Previous works in

this area span many ﬁelds. Some well known ﬁelds

include maglev transportation (Luguang, 2002), mi-

crorobotics (Khamesse et al., 2002), photolitography

(Kim and Trumper, 1998), positioning (Suk and Baek,

2002), launch systems (Jacobs, 2001) and so on.

In general a maglev system can be classiﬁed, based

on the levitation forces, as an attractive system or a

repulsive one, each type having various kinds of pos-

sible arrangements. Most of the maglev systems dis-

cussed in the literature are attractive, where attrac-

tive forces are applied between the moving carriage

Research partially supported by CONACYT under

Grant 44969 and by CINVESTAV

and ﬁxed guide tracks. On the other hand, the repul-

sive maglev systems use repulsive forces to push the

moving carriage above the ﬁxed guide tracks. How-

ever, a magnetic levitation system is highly nonlinear

and unstable, and a feedback control is necessary to

achieve a stable operation. Many works have devel-

oped linear controllers, and the control laws have been

based on traditional control methods and only local

stability is guaranteed. These developed controllers

may not meet the precision control purpose for ma-

glev systems, because these systems are naturally un-

der the inﬂuence of many uncertainties. On the other

hand, the works that use nonlinear mathematical mod-

els (Kaloust et al., 2004) only control 2 DOFs and

consider the other DOFs stables.

To overcome this problem, a new approach called

“second order sliding mode (SOSM)” has been pro-

posed (Elmali and Olgac, 1992; Bartolini et al., 2001;

Castro-Linares et al., 2004). This approach has the

main advantages of the standard sliding mode con-

trol technique, the chattering effect is eliminated and

a high order precision is provided.

In this paper the kind of maglev system is a repul-

sive one, using an arrangement of a permanent mag-

net levitated above an electromagnet. The control de-

sign proposed here is based on SOSM control tech-

nique for the nonlinear maglev mathematical model;

this controller is robust when different loads are put

on the carrier and guarantees stabilization and preci-

sion positioning.

The organization of this paper is as follows. In sec-

tion II, the maglev system is described, some magnet-

Alvarez-Sanchez E., Alvarez-Gallegos J. and Castro-Linares R. (2005).

MODELING AND CONTROLLER DESIGN OF A MAGNETIC LEVITATION SYSTEM WITH FIVE DEGREES OF FREEDOM.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 99-106

DOI: 10.5220/0001184100990106

 SciTePress

ics formulas will be reviewed and the mathematical

model is obtained. In section III a SOSM controller is

designed using the nonlinear system obtained. Sec-

tion IV presents numerical simulations results that

show the robustness of the controller designed. Fi-

nally conclusions are given in section V.

2 SYSTEM MODELING

In this section, the mechanical structure of a Maglev

system will be described. Its analytical model of 5

DOFs will be derived and analyzed. The 6th DOF,

propulsion in the y direction, will be analyzed and

controlled in a future work. The overall system is

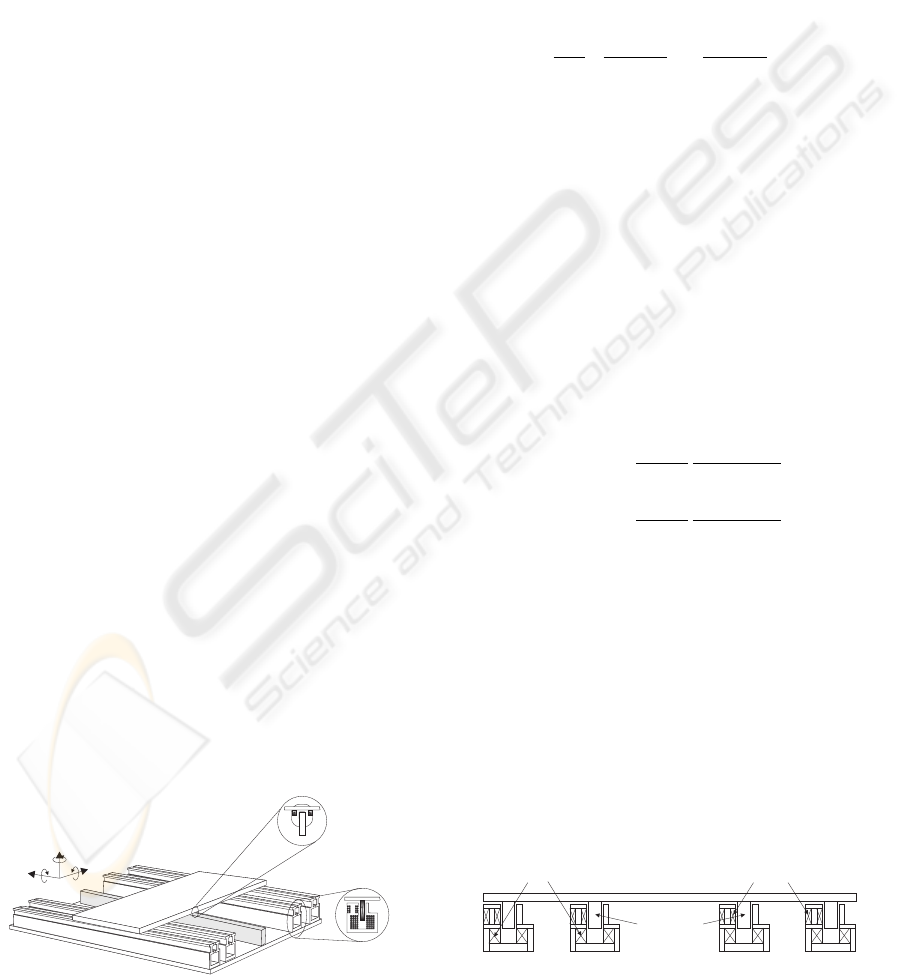
shown in Fig.1.

2.1 Maglev system

Basically, the maglev system proposed here is a multi-

input multi-output (MIMO) system. Here, the states

are the lateral and vertical displacement, x and z re-

spectively, and the three rotations θ, ψ and φ. The

outputs are x, θ, z, ψ and φ while the inputs are the

currents applied to coils into the levitation guiding

tracks. The dynamics of the maglev system can be

divided into a stable part and an unstable one. The

stable part consists of the dynamic of z, while the un-

stable part consists of the dynamics of x, θ, ψ and φ.

In order to control 3 DOFs in rotational displace-

ment and 2 DOFs in lateral displacement, i.e., a total

of 5 DOFs of the carrier separately, a four-track de-

sign, shown in Fig.2, is sufﬁcient to supply such 5-

DOFs control. The guiding tracks together must pro-

vide a levitation force to counteract the carrier weight.

On the other hand, to provide a uniform magnetic

ﬁeld along the guiding tracks, an oblong coil is nec-

essary.

Also, due to the nature of lateral instability of a re-

pulsive system, stabilizers are needed inside.The sta-

bilizers can control the lateral position of a levitat-

ing NdFeB magnet whereas the levitator can control

the vertical (up-down) position of a levitating NdFeB

magnet.

Carrier

Guidingtrack

PropulsionDevice

Figure 1: 3D view of maglev system

The four stabilizing coils are grouped into two sets:

inner guiding tracks and outer guiding tracks. Then,

the principle shown in Figs.3 and 4 to control the ro-

tation of the carrier about a vertical axis and its lateral

translation can be used.

In order to obtain the magnetic force in z and x

is necessary to analyze some magnetic formulas. Ac-

cording to Biot-Savart’s law and Ampere’s circuit law

(Nayef and Brussel, 1985) the magnetic ﬂux density

in any point around an inﬁnitely long current-carrying

straight wire at a point (x,z) can be obtained as

B =

2π



−z

+ z

i +

+ z



(1)

where µ

is the permeability of free space, I is the in-

put current,

i and

k are the unit vector in the Cartesian

coordinate.

If we deal with a permanent magnet as a single di-

pole moment, the expression of the Lorentz force F

exerted on the permanent magnet by an external mag-

netic ﬁeld B can be characterized by the following

vector equation

F = (u · ∇) B (2)

where u is the dipole moment of the permanent mag-

net. Assuming that the dipole lies in the z direction,

useful scalar equations of the force components can

be derived from (2) as

2π



− x



+ z

)

(3)

−xz

+ z

)

(4)

2.2 Nonlinear model

Consider a carrier represented by an uniform box-

shaped object with the center of mass coincident with

the center of geometry. The principle of linear mo-

mentum leads to the following equations:

= m¨x, F

= m¨z (5)

where F

and F

are the resultant forces acting on the

carrier along the x-axis and z-axis, respectively, and

m is the mass of the carrier.

carrier

TrackA TrackB TrackDTrackC

levitationcoils

stabilizingcoils

permanent

magnets

Figure 2: Front view of the maglev system

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

100

FZA FZB FZDFZC FZAFZBFZD FZC

Figure 3: Magnetic levitation forces

A B

C D

Fxad FxbdFxas Fxbs

Fxcd Fxcs Fxdd Fxds

Figure 4: Destabilizing and stabilizing forces

By the same token, the principle of angular mo-

mentum leads to torque equations for the rotational

coordinates

= J

θ, T

= J

ψ, T

= J

φ (6)

where T

and T

are the external torques, J

, J

and J

are the principal moments of inertia and θ, ψ

and φ are the three angular rotation of the rigid body.

To understand the dynamics of the maglev system

it is necessary to describe an arbitrary orientation of

the carrier in space. This orientation can be obtained

using the Euler angular description yaw(θ)-roll(ψ)-

pitch(φ) given by the following rotation matrix

R =

cθcψ cθsψsφ − sθcφ

sθcφ sθsψsφ + cθcφ

−sψ cψsφ

cθsψcφ + sθsφ

sθsψcφ − cθsφ

cψcφ

(7)

where c and s represents cos and sin respectively.

The position of the levitation magnets on the carrier

are

A (−b

, a, 0) B (b

, a, 0)

C (−b

, −a, 0) D (b

, −a, 0)

where A, B, C and D denote the center position of

these magnets and a, b

and b

are known dimensions.

If one assumes small pitch, roll and yaw angle for the

carrier, in additional to x and z translation, the posi-

tion of the magnets on the carrier can be calculated

(x,y,z)a

−b

− aθ + x

a − b

ψ + aφ + z

(x,y,z)b

− aθ + x

a + b

−b

ψ + aφ + z

(x,y,z)c

−b

+ aθ + x

−a − b

ψ − aφ + z

(x,y,z)d

+ aθ + x

−a + b

−b

ψ − aφ + z

(8)

In similar form, the positions of the magnets into the

guiding tracks, shown in Fig.5, are obtained as

a,b

−aθ + d

ψ + x

a − d

aφ + d

+ z

c,d

aθ + d

ψ + x

−a − d

−aφ + d

+ z

(9)

Before formulating equations of motion, some nota-

tions on force and distances are explained in the fol-

lowing: the force subscript has two letters, the ﬁrst

means the label of the magnet, and the second the

magnetic force type, d for destabilizing, s for stabi-

lizing and l for levitation, e.g. F

is the destabilizing

force applied to the magnet A caused by the levita-

tion coil A . The position of the magnets, denoted by

b, has a subscript with two letters, the ﬁrst means the

direction of the distance and the second the label of

the magnet, e.g. b

is the distance in the x direction

from the carrier center to the center of the magnet A.

By substituting the positions of the levitation mag-

net (9) into the magnetic force equations (3) and (4)

one can get the forces exerted on each levitation mag-

net. Next, one can substitute these force equations

into the dynamics of the carrier, and then the equa-

MODELING AND CONTROLLER DESIGN OF A MAGNETIC LEVITATION SYSTEM WITH FIVE DEGREES OF

FREEDOM

101

Figure 5: Guiding track

tions of motion can be obtained as

¨x = F

+ F

θ = −b

− b

−b

+ b

¨z = F

+ F

− m

ψ = b

− w

) − b

− w

)

− w

) − b

− w

)

−b

− b

−b

− b

−b

− b

φ = b

− w

) + b

− w

)

−b

− w

) − b

− w

)

(10)

where g is the acceleration due to gravity, m

is the

mass of the carrier and load, J represents the mo-

ment of inertia of the carrier, w represents the weight

above each magnet, I

is the current in the inner sta-

bilizer whereas I

is the current in the outer stabi-

lizer. I

, I

represent the currents in the levita-

tors corresponding to the levitation magnets A, B, C

and D respectively. F

represents the damping force

produced by the levitation coils and can be modeled

as F

= −K

dam

˙z, where K

dam

is a positive constant.

3 CONTROLLER DESIGN

In this section , a control scheme is presented for the

levitation an stabilization dynamics of the magnetic

system described in section 2. The aim is to control

the height z while the lateral and rotational displace-

ments are tried to be kept near to zero. For doing this

a SOSM proposed in (Elmali and Olgac, 1992) is ap-

plied to the nonlinear model (10). For symplicity, the

currents in the levitation coils A and B are set to be

same, thus I

= I

. One also deﬁnes the state

vector ρ =

x ˙x θ

θ z ˙z ψ

ψ φ

together with the

input vector u = [I

]

and the output

vector y = [x θ z ψ φ]

. The nonlinear model (10)

can then be rewritten in the state space form

˙ρ = f (ρ) + ∆f (ρ) +

i=1

(ρ) + ∆g

(ρ)] u

y = h (ρ) (11)

where

f (ρ) = col



˙x, 0,

θ, 0, ˙z,



−g −

dam

˙z



ψ, 0,

φ, 0

∆f (ρ) = col[0, 0, 0, 0, 0, ∆f

(ρ), 0, 0, 0, 0]

(ρ) =







−b







(ρ) =







−b







(ρ) =







−b







ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

102

(ρ) =







−b







(ρ) =







−b







∆g

(ρ) =







∆g

(ρ)

∆g

10j

(ρ)







j = 1, . . . , 5

h (ρ) = [ρ

]

∆f (ρ) and ∆g

(ρ) represent modeling uncertainties

associated to the magnetic system. Equation (11) can

also be written in a more condensed form as

˙ρ = f (ρ) + ∆f (ρ) + [G (ρ) + ∆G (ρ)] u

y = h (ρ) (12)

where

G (ρ) = [g

(ρ) . . . g

(ρ)]

∆G (ρ) = [∆g

(ρ) . . . ∆g

(ρ)]

The goal is to make the output y (ρ) in system (12)

follow a desired trajectory y

(t). The control strat-

egy should be robust enough to handle the modeling

uncertainties ∆f and ∆G. The upper bounds of these

equations are assumed to be

|∆f

(ρ)| ≤ σ (ρ)

|∆g

(ρ)| ≤ α

(ρ) i = 1, . . . , 10

j = 1, . . . , 5 (13)

When the modeling uncertainties are not considered,

this is ∆f (ρ) = 0 and ∆G (ρ) = 0, one has the exact

model

˙ρ = f (ρ) + G (ρ) u

y = h (ρ) (14)

for which one can easily verify, in accordanace to

(Isidori, 1995) that it has a (vector) relative degree

, r

] = [2, 2, 2, 2, 2] at a point ρ

= 0. In

particular the decoupling matrix A (ρ) is given by

A (ρ) =







· · · a







(15)

where

= L

= g

(2i)j

(ρ) i, j = 1, . . . , 5

which is nonsingular at ρ = 0. One can also verify

that, for the uncertain system (12),

∆f (ρ) and

∆G (ρ) ∈ Ker

, dL

, . . . , dL

−2

(16)

for i = 1, . . . , 5. This is, the so-called matching con-

dition is achieved. Thus the uncertainties ∆f and ∆G

do not appear in the time derivatives of y

of order

less than r

= 2 and the (vector) relative degree is

unchanged. Besides, since

i=1

= 10, system

(12) has no unobservable internal dynamics. Follow-

ing (Elmali and Olgac, 1992), a SOSM strategy that

allows to have reference output tracking despite the

presence of the uncertainties can be obtained by set-

ting

˙s

+ z

= ˙e

+ c

j = 1, . . . , 5 (17)

where s

= ˙s

= 0 represents the jth sliding surface

and e

= y

− y

is the jth tracking error, with y

being the jth component of the desired output y

. The

constant real coefﬁcients c

and c

are chosen in

such a way that the polynomial π

+ c

π + c

= 0

is Hurtwitz. z

is also a constant real coefﬁcient.

By choosing a Lyapunov function candidate as



˙s

˙s + ω



for j = 1, . . . , 5 (18)

where s = [s

, . . . , s

]

and ω

is a real coefﬁcient,

one has that, the Lyapunov stability criterion leads to

the condition

˙s



¨s + ω



≤ 0 (19)

which is known as the attractivity condition towards

s = ˙s = 0. By setting

¨s = −Ksgn ( ˙s) − ω

(20)

where K is a real positive number different from zero

and sgn ( ˙s) = [sgn ( ˙s

) , . . . , sgn ( ˙s

)]

, one can as-

sures the fulﬁllment of condition (19). From this last

MODELING AND CONTROLLER DESIGN OF A MAGNETIC LEVITATION SYSTEM WITH FIVE DEGREES OF

FREEDOM

103

equation and considering the exact model (14) one has

the sliding control u = u

given by

= −A

−1

(ρ)

F (ρ) + CE − y

(r)

− z

˙s

−A

−1

(ρ)



Ksgn ( ˙s) + ω



(21)

where

F (ρ) =



















−g −

dam







CE =







+ c

˙e

+ c

˙e







= [¨y

. . . ¨y

]

For the uncertain system (12) (this is ∆f 6= 0 and

∆G 6= 0), when the sliding control u

is substituted

into (19), the attractivity condition takes the form

˙s



−K



I + ∆A (ρ) A

−1

(ρ)



sgn ( ˙s)

+∆A (ρ) A

−1

(ρ) (bv − F (ρ)) + ∆F (ρ)



< 0

(22)

where

∆A (ρ) =







∆g







j = 1, . . . , 5

∆F (ρ) =







∆f













∆f







bv = y

− CE + z

˙s − ω

One can notice that ˙s

sgn ( ˙s)≥k ˙sk, thus

−K ˙s

sgn ( ˙s)≤−K k ˙sk, and (22) can be reiter-

ated using vector norms obtaining

−K + K



∆AA

−1

sgn ( ˙s)



∆AA

−1

(bv − F )



+ k∆F k ≤ −µ (23)

where µ > 0. This last expression leads to the follow-

ing

K ≥



∆AA

−1

(bv − F )



+ k∆F k + µ

1 − k∆AA

−1

sgn ( ˙s)k

(24)

were it is assumed that



∆AA

−1

sgn ( ˙s)



< 1.

4 SIMULATION RESULTS

In this section, a series of simulation are proposed

for the maglev system using the SOSM controller de-

signed in the previous section. The simulation para-

meters are listed in table 1. The desired values for

all states are equal to zero, this means that the perma-

nent magnets are regulated at the center of the guid-

ing tracks whereas the carrier is located in the center

of the system.

The ﬁrst simulation was made with no load pertur-

bations and with the initial conditions x (0) = 2 mm,

θ (0) = 25 mrad, z (0) = −8 mm, ψ (0) =

35 mrad and φ (0) = −25 mrad. Figures 6 and 7

show that all the states converge to zero as t goes to

inﬁnity. Figures 8 and 9 show the levitation and sta-

bilization control currents, respectively. In Fig.9 one

can notice that the stabilization control currents have

a zero value at steady state, this means that permanent

magnets are located at the center of the guiding tracks,

where the destabilizing forces are equal to zero.

The second simulation tests the capability of load

disturbance rejection. The load disturbance is applied

on the carrier over each levitation magnet (see ﬁgures

3 and 4) after the carrier reaches a steady-state. Dis-

turbances of 0.25 Kg are introduced at 0.3s, 0.6 s, 1

s and 1.5 s. In this case, the initial conditions were

x (0) = 2 mm, θ (0) = 2.5 mrad, z (0) = −8 mm,

psi (0) = 3.5 mrad and φ (0) = −2.5 mrad. Figu-

res 10 and 11 show the response of the maglev system

when a load disturbance is applied on the carrier. One

can observe that all the states go to equilibrium points

when the load disturbance increases. Fig.12 shows

the changes in the levitation control currents due to

different load disturbances; one can observe the in-

crements or decrements in the current magnitude after

the load disturbance increases. Fig.13 shows that the

currents in both stabilizers do not present any change,

this is because the load does not affect the x transla-

tion and the θ rotation.

0 0.1 0.2 0.3 0.4 0.5

−8

−6

−4

−2

time (s)

distance (mm)

Figure 6: Carrier motion in x and z without load distur-

bances

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

104

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

−30

−20

−10

time (s)

rotation (mrad)

Figure 7: Carrier rotations θ, ψ and φ without load distur-

bances

0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5

−0.5

0.5

1.5

2.5

time (s)

current (amp)

Figure 8: Levitation currents A, C and D without load dis-

turbances

5 CONCLUSIONS

In this paper a nonlinear mathematical model for a

maglev system has been derived. A repulsive ma-

glev system with four guiding tracks is adopted here.

There, the maglev system has been treated as a MIMO

system, and a SOSM controller for a nonlinear 5

DOFs maglev system has been designed here. From

the simulation results, the feasibility and effectiveness

of the designed controller have been clearly shown.

The desired performances of levitation and lateral and

rotational stabilization have been achieved. Future

work includes experimental laboratory tests.

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

−2

−1.5

−1

−0.5

0.5

1.5

time (s)

current (amp)

Figure 9: Stabilization currents 1 and 2 without load distur-

bances

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

−8

−7

−6

−5

−4

−3

−2

−1

time (s)

distance (mm)

Figure 10: The carrier motion with load disturbances

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

−3

−2

−1

time (s)

rotation (mrad)

Figure 11: Carrier rotations with load disturbances

REFERENCES

Bartolini, G., Ferrara, A., Pisano, A., and Usai, E. (2001).

On the convergence properties of a 2-sliding control

algorithm for non-linear uncertain systems. In Inter-

national Journal of Control, vol. 74, no.7, pp. 718-

731. Taylor Francis Ltd.

Castro-Linares, R., Glumineau, A., Laghraouche, S., and

Plestan, F. (2004). Higher order siding mode oberver-

based control. In in 2nd Symposium on System, Struc-

ture and Control, Oaxaca, Mexico, pp. 517-522.

Elmali, H. and Olgac, N. (1992). Robust output tracking

control of nonlinear mimo systems via sliding mode

technique. In Automatica, vol. 28, no. 1, pp. 145-151.

Pergamon Press plc.

Isidori, A. (1995). Nonlinear Control Systems. Springer

Verlag, New York, 3rd edition.

Jacobs, W. A. (2001). Magnetic launch assist-nasa’s vision

for the future. In IEEE Transactions on Magnetics,

vol. 37, no. 1, pp. 55-57.

Kaloust, J., Ham, C., Siehling, J., Jongekryg, E., and Han,

Q. (2004). Nonlinear robust control design for levi-

tation and propulsion of a maglev system. In in IEE

Proc. Control Theory Appl., vol. 151, no.4, pp. 460-

464. IEE.

Khamesse, M. B., Kato, N., Kamura, Y., and Nakamura, T.

(2002). Design and control of a microrobotic system

using magnetic levitation. In IEEE/ASME Transac-

tions on Mechatronics, vol. 7, no. 1, pp. 1-14. IEEE.

MODELING AND CONTROLLER DESIGN OF A MAGNETIC LEVITATION SYSTEM WITH FIVE DEGREES OF

FREEDOM

105

Kim, W.-J. and Trumper, D. L. (1998). High-precision mag-

netic levitation stage for photolithography. In Preci-

sion Engineering, vol. 22, no. 2, pp. 66-77. Elsevier

Science Inc.

Luguang, Y. (2002). Progress of high-speed maglev in

china. In IEEE Transactions on Applied Supercon-

ductivity, vol. 12, no. 1, pp. 944-947. IEEE.

Nayef, M. H. and Brussel, M. K. (1985). Electricity and

Magnetism. John Wiley and Sons, Inc., New York.

Suk, K. and Baek, Y. S. (2002). Contact-free moving-

magnet type of micropositioner with opimized spec-

iﬁcation. In IEEE Transactions on Magnetics, vol. 38,

pp. 1539-1548.

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

0.5

1.5

2.5

time (s)

current (amp)

Figure 12: Behavior of the levitation A, C and D currents

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

−2

−1.5

−1

−0.5

0.5

time (s)

current (amp)

Figure 13: Behavior of the stabilization 1 and 2 currents

Table 1: System parameters

Mass m 1.0536 Kg

Carrier dimension 405 x 205 x 6 mm

NdFeB Size 13.91 x 31.62 x 25.4 mm

NdFeB Br 1.19 T

Turns of levitator 240 turns

Turns of stabilizer 120 turns

diameter of wire 0.71 mm

a, b

, b

70, 81, 175 mm

, d

12, 15, 17 mm

, c

2,2,1,2,2

, c

50,40,40,50,50

K,K

dam

170, 27

, z

75, 0.7

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

106