OPTIMAL CONTROL APPLIED TO OPTIMIZATION
OF MOBILE SWITCHING SURFACES
PART II : APPLICATIONS
C
´
eline Qu
´
emard*
Jean-Claude Jolly*
*LISA-FRE 2656 CNRS
62, avenue Notre-Dame du Lac - F49000 Angers
Keywords:
Hybrid Dynamical System, Optimization, Mobile Switching Surface, Thermostat with Anticipative Resis-
tance, Car with Two Gears, Robot, Obstacle Avoidance, Target Approach.
Abstract:
To reinforce interest of a general optimization algorithm obtained in a previous paper (Jolly et al., 2005),
we consider three applications : an original one about control of cycles for a thermostat with anticipative
resistance, a classical one with a new resolution for a car with two gears and a last one about an obstacle-
avoidance problem in robotics. For the first case, we optimize the adjustment of thermostat thresholds to
control at best the room temperature. For the second case, we optimize the switching times to stop the car as
near as possible of chosen points and this, in a minimum time . In the last example, we optimize parameters
of the switching surfaces in order that the robot reaches a chosen target without meeting a mobile obstacle.
1 INTRODUCTION
In (Jolly et al., 2005), we have found results on the
question of optimization of switching surfaces for a
hybrid dynamical system (h.d.s), generalizing what
was in (Wardi et al., 2004).
Here, we consider three applications that underline
interest of these theorical results. The first, somewhat
original, is one of a thermostat with anticipative resis-
tance controlling a convector in a same room (C
´
ebron,
2000), (Qu
´
emard et al., 2005). In this example, we
optimize the adjustment of thermostat thresholds to
control at best the room temperature. This applica-
tion can be taken as a pattern for h.d.s leading to some
cycle solutions.
The second application is one of a car with two
gears (Gapaillard, 2003), (Hedlund and Rantzer,
2002). We optimize the switching times, firstly, to
stop the car as near as possible of a first desired des-
tination and then, after a new start-up, to stop the car
as near as possible of a final destination and this, in a
minimum time. Interest of this classical h.d.s problem
for us is to bring a new resolution improving numeri-
cal performance.
The last application solves an obstacle avoidance
problem in robotics (Boccadoro, 2004). Here, we
optimize parameters of the switching surfaces in or-
der that a robot reaches a pre-specified target without
never meating a given mobile obstacle. Compared to
(Boccadoro, 2004) where the considered obstacle is
fixed, this example underlines interest of mobility for
switching surfaces in applications.
In section 2, we briefly present the theorical algo-
rithm found in (Jolly et al., 2005). From section 3 to
section 5, we detail each application presented above.
Section 6 concludes the paper.
2 OPTIMIZATION ALGORITHM
REMINDER
Let t
0
, x
0
= x(t
0
) ∈ R
n
be given initial time
and state. Here, we consider a h.d.s which sustains
switchings at increasing times t
1
, ..., t
N
in [t
0
, t
N+1
]
(t
N+1
is the final time) so that for i = 1, ..., N + 1,
state x
i
= x(t
i
) belongs to a given mobile surface
parameterized by a
i
∈ R
r
i
and of equation:
Ψ
i
(x
i
, t
i
, a
i
) = 0, (1)
where Ψ
i
is from C
1
class with values in R. In
[t
0
, t
N+1
], state x(t) is supposed to be continuous and
in [t
i−1
, t
i
], i = 1, ..., N +1, state x(t) complies with
dynamical system:
˙x = f
i
(x, t), (2)
372
Quémard C. and Jolly J. (2005).
OPTIMAL CONTROL APPLIED TO OPTIMIZATION OF MOBILE SWITCHING SURFACES PART II : APPLICATIONS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 372-377
DOI: 10.5220/0001184703720377
Copyright
c
 SciTePress

where f
i
is from C
1
class with values in R
n
. Un-
der suitable assumptions (Jolly et al., 2005), t
i
is a
function of a
1
, ..., a
i
, i = 1, ..., N + 1. For our opti-
mization problem, the criterion we have to minimize
or maximize is in the form:
J
0
=
N+1
X
i=1
J
0
i
,
where J
0
i
= φ
i
(x
i
, t
i
, a
i
) +
R
t
i
t
i−1
L
i
(x, t)dt with φ
i
and L
i
from C
1
class.
Optimization problem - Considering t
i
as a function
of a
1
, ..., a
i
, i = 1, .., N + 1, we search values for
a
1
, ..., a
N+1
which optimize criterion J
0
.
We consider the following augmented criterion:
N+1
X
i=1
J
i
, J
i
= φ
i
+ ν
i
Ψ
i
+
Z
t
i
t
i−1
(H
i
− λ
T
i
˙x)dt (3)
where ν
i
is a control parameter, λ
i
is the adjoint state
and H
i
= L
i
+ λ
T
i
f
i
. Those variables play a key role
in the following algorithm:
Let a
1
, ..., a
N+1
be initialized parameters.
1. We solve system (2) forwards for i = 1, .., N + 1.
In the same time, we compute switching times t
i
,
i = 1, .., N + 1, with constraint (1).
2. Starting from t
N+1
, x
N+1
= x(t
N+1
) just ob-
tained, we solve system (4) backwards given by:
∂H
i
∂x
+
˙
λ
T
i
= 0, i = N + 1, .., 1. (4)
In the same time, we compute suites ν
i
, λ
i
, i =
N + 1, .., 1 given by:







ν
i
= −(L
i
− L
i+1
+ λ
T
i+1
(f
i
− f
i+1
)
+
∂ϕ
i
∂X
i
f
i
+
∂ϕ
i
∂t
i
)
t
i
(
∂Ψ
i
∂X
i
f
i
+
∂Ψ
i
∂t
i
)
−1
t
i
,
λ
T
i
(t
i
) = λ
T
i+1
(t
i
) +
∂ϕ
i
∂X
i
+ ν
i
∂Ψ
i
∂X
i
,
(5)
i = N + 1, .., 1. The notation used is that variable
t
i
, which follows an expression in a lower position,
means that this expression is evaluated at t
i
, x(t
i
).
In (5), to start the backward recurrence, we define:
λ
N+2
(t
N+1
) = 0 , L
N+2
|
t
N+1
= 0. (6)
3. Then, with all elements computed in the previous
steps, we can deduce:
dJ
0
da
i
=
dJ
da
i
=
∂φ
i
∂a
i
+ ν
i
∂Ψ
i
∂a
i
, i = 1, ..., N + 1.
(7)
4. Finally, with the criterion gradient, we apply a de-
scent method to obtain optimal results.
3 OPTIMIZATION OF LIMIT
CYCLES. APPLICATION TO A
THERMAL DEVICE
3.1 Studied Thermal Device
Figure 1 represents a thermostat with anticipative re-
sistance controlling a convector located in the same
room. Such a thermostat is common in the industrial
market (Cyssau, 1990). The principle is the follow-
ing. The thermostat, which is controlled by a hystere-
sis phenomenon (Figure 1), heats the room through
a convector (power P
c
) and itself through a resis-
tance (power P
t
) until its temperature reaches its up-
per threshold. Then, it switches off until its tempera-
ture reaches its lower threshold.
c o n v e c t o r :
t e m p e r a t u r e
z
,
p o w e r
P
c
o u t s i d e
t e m p e r a t u r e :
q
e
t h e r m o s t a t :
t e m p e r a t u r e
x
,
p o w e r
P
t
( o f
a n t i c i p a t i v e
r e s i s t a n c e )
r o o m :
t e m p e r a t u r e
y
c o n v e c t o r :
t e m p e r a t u r e
z
,
p o w e r
P
c
o u t s i d e
t e m p e r a t u r e :
q
e
t h e r m o s t a t :
t e m p e r a t u r e
x
,
p o w e r
P
t
( o f
a n t i c i p a t i v e
r e s i s t a n c e )
r o o m :
t e m p e r a t u r e
y
c o n v e c t o r :
t e m p e r a t u r e
z
,
p o w e r
P
c
o u t s i d e
t e m p e r a t u r e :
q
e
t h e r m o s t a t :
t e m p e r a t u r e
x
,
p o w e r
P
t
( o f
a n t i c i p a t i v e
r e s i s t a n c e )
r o o m :
t e m p e r a t u r e
y
c o n v e c t o r :
t e m p e r a t u r e
z
,
p o w e r
P
c
o u t s i d e
t e m p e r a t u r e :
q
e
t h e r m o s t a t :
t e m p e r a t u r e
x
,
p o w e r
P
t
( o f
a n t i c i p a t i v e
r e s i s t a n c e )
r o o m :
t e m p e r a t u r e
y
1
q
1
q
2
x
q
0
1
q
1
q
2
x
q
0
Figure 1: Thermal process and hysteresis variable
With notations of Figure 1, a power assessment
and Newton law give, in the state form proposed in
(C
´
ebron, 2000), the following system:























˙x
˙y
˙z
!
=
−a a 0
0 −(b + d) b
0 c −c
!
x
y
z
!
+q
p
t
0
p
c
!
+
0
θ
e
0
!
ξ = (
1 0 0
)
x
y
z
!
= x
(8)
with numerical values set: a = 0.001 s
−1
, b = 2.81
10
−4
s
−1
, c = 0.011 s
−1
, d = 0, 2 10
−4
s
−1
, p
t
=
0.0035 K.s
−1
, p
c
= 0.1 K.s
−1
, θ
e
= 274.d K.s
−1
.
Here, we consider two heating ways, say a day one
and a night one, each one having its own lower (θ
1
for
the day, θ
3
for the night) and upper (θ
2
for the day, θ
4
for the night) threshold. We also consider here that
we change the way of heating at t = 20000 s.
Discrete variable q takes the value 0 or 1. Here,
we are in the same situation that the one exposed in
OPTIMAL CONTROL APPLIED TO OPTIMIZATION OF MOBILE SWITCHING SURFACES PART II :
APPLICATIONS
373

the second section with t
1
< t
2
... < t
N
switching
times in [t
0
, t
N+1
], where t
0
and t
N+1
are respec-
tively initial and final times. A simulation with Mat-
lab, with q
0
= 1 at t
0
= 0 and with initial values
X(t
0
) = (288 288 288)
T
, θ
1
= 293 K, θ
2
= 294
K, θ
3
= 290 K, θ
4
= 291 K gives Figure 2.
0 1 2 3 4 5 6
x 10
4
288
289
290
291
292
293
294
Time (s)
Temperatures (K)
thermostat temperature
room temperature
desired room average temperature (day)
desired room average temperature (night)
desired temperature at odd switching instants (day)
desired temperature at odd switching instants (night)
switchings on thermostat temperature
switchings on room temperature
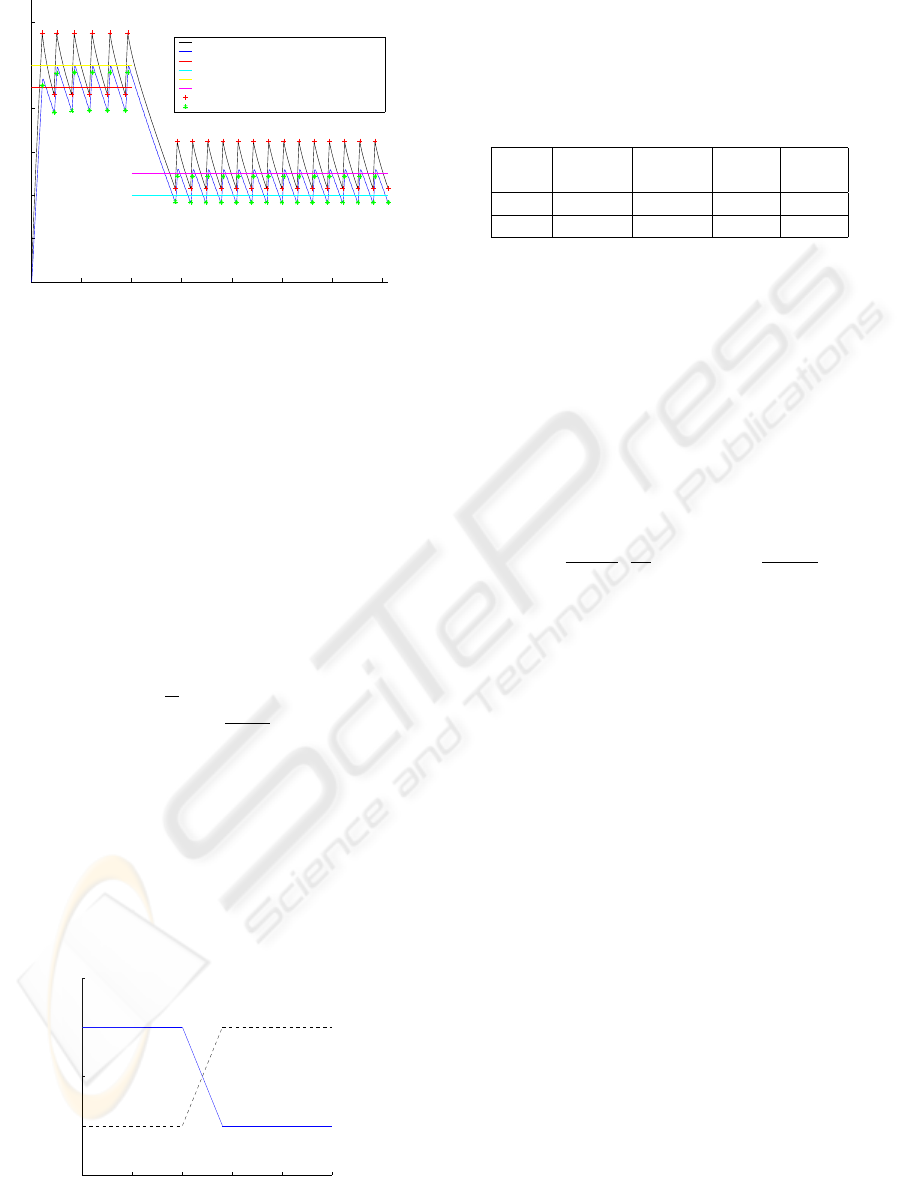
Figure 2: Temperatures before optimization
Optimization problem - How can we choose thermo-
stat thresholds (considered not fixed) θ
i
, i = 1, ..., 4
to have the room temperature at odd switching times
(upper stars) as near as possible of desired tempera-
tures θ
u1
= 293 K (for the day), θ
u2
= 290.5 K (for
the night)? Moreover, in the same time, how can we
choose them to have the room average temperature
as near as possible of desired room average tempera-
tures θ
d1
= 292.5 K (for the day), θ
d2
= 290 K (for
the night)?
3.2 Gradient Calculus. Criterion
Minimization
Results obtained in (Qu
´
emard et al., 2005) and Figure
2 let us to establish that thermostat model is a h.d.s for
which a trajectory X(t) can converge towards a stable
limit cycle. Following notations used in the second
section and particularly in equation (3), we can con-
sider the augmented criterion J =
P
N+1
i=1
J
i
, with:
J
i
= q
i
α
N + 1
(EX
i
− θ
uj
)
2
+ ν
i
1
N + 1
(DX
i
− a
i
)
+
1
t
N+1
Z
t
i
t
i−1
(H
i
− λ
T
i
˙
X
i
)dt,
where:
• q
i
= 0 if i is even and q
i
= 1 if i is odd,
• D = (1 0 0), E = (0 1 0),
• a
i
= θ
1
if i is even and if t
i
< 20000, a
i
= θ
2
if i
is odd and if t
i
< 20000, a
i
= θ
3
if i is even and if
t
i
≥ 20000, a
i
= θ
4
if i is odd and if t
i
≥ 20000,
• H
i
= L
i
+ λ
T
i
f
i
, where L
i
= β(EX
i
− θ
dj
)
2
,
f
i
= AX
i
+ q
i
B + C,
• α + β = 1, α > 0, β > 0,
• j = 1 if t
i
< 20000 and j = 2 if t
i
≥ 20000.
From there, we apply the algorithm we report in the
second section to obtain an optimal trajectory X(t)
for J as a function of θ
1
, θ
2
, θ
3
, θ
4
.
Firstly, for arbitrary initial conditions, we solve direct
system (8), variable with i and we compute switching
times and states and the final time and state. Secondly,
we solve adjoint system (4) backwards given here by:
˙
λ
T
i
= −A
T
λ
T
i
− (0 2(EX
i
− θ
dj
) 0)
T
.
In the same time, we can define ν
i
, λ
i
(t
i
) with equa-
tions systems (5) and (6):











ν
i
= −
N+1
Df
i
(β((EX
i
− θ
dj
)
2
− (EX
i+1
− θ
dk
)
2
)
+λ
T
i+1
(f
i
− f
i+1
) + q
i
2α
N+1
(EX
i
− θ
uj
)Ef
i
),
λ
T
i
(t
i
) = λ
T
i+1
(t
i
) + q
i
2α
N+1
(EX
i
− θ
uj
)E
+
ν
i
N+1
D,
where k = 1 if t
i+1
< 20000, otherwise k = 2.
Thus, from (7), we can deduce:
dJ
0
i
da
i
= −
ν
i
N + 1
, i = 1, .., N + 1.
Regrouping those terms according to values of t
i
and
to parity of i, we obtain the criterion gradient. Thus,
we can apply a descent methode to define an optimal
solution. The using of Matlab and particularly of
function fmincon with initial values α = β = 0.5,
θ
1
= 293K, θ
2
= 294K, θ
3
= 290K, θ
4
= 291K,
gives after thirteen iterations the algorithm end. We
obtain Figure 3 and the following optimal values:
(θ
1
, θ
2
, θ
3
, θ
4
) =(292.32, 293.744, 290.149, 291.249),
J
0
= 18.5046.
This optimization leads to the following differences
(indexed quantities rely on switching quantities):
• Initially (Figure 2): |EX
i
−θ
u1
| ≃ 0.2872, |EX
i
−
θ
u2
| ≃ 0.1378. Moreover, |θ
m1
− θ
d1
| ≃ 0.4371
K for t < 20000 and |θ
m2
− θ
d1
| ≃ 0.0132 K
for t ≥ 20000 whith θ
m1
and θ
m2
corresponding
respectively to the obtained room average tempera-
ture for t < 20000 and for t ≥ 20000.
• After optimization (Figure 3): |EX
i
− θ
u1
| ≃
0.0222, |EX
i
− θ
u2
| ≃ 0.0865. Moreover, |θ
m1
−
θ
d1
| ≃ 0.0362 K for t < 20000 and |θ
m2
− θ
d1
| ≃
0.2058 K for t ≥ 20000. So, just this last result is
not improved.
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
374

0 1 2 3 4 5 6 7
x 10
4
288
289
290
291
292
293
294
Time (s)
Temperatures (K)
thermostat temperature
room temperature
desired room average temperature (day)
desired room average temperature (night)
desired temperature at odd switching instants (day)
desired temperature at odd switching instants (night)
switchings on thermostat temperature
corresponding switchings on room temperature
Figure 3: Temperatures after optimization
4 OPTIMIZATION OF
SWITCHING TIMES.
APPLICATION TO A CAR
WITH TWO GEARS
4.1 Studied Car Model
Following (Hedlund and Rantzer, 2002), we consider
the following system:



˙x
1
= x
2
˙x
2
=
1
m
(−cx
2
+ kx
3
)
˙x
3
= −x
2
+
g
q
(x
2
)
k
u
(9)
where q = 1, 2. In (Hedlund and Rantzer, 2002), the
authors find that optimal input throttle u ∈ [−0.1, 1.1]
is essentially a bang-bang pattern what we take in as-
sumption. So, here, we choose u ∈ {−0.1, 1.1}.
The three continuous states of the system repre-
sent respectively the car position (x
1
), the car velocity
(x
2
) and the rotational displacement of its transmis-
sion shaft (x
3
). Function g
q
, plotted in Figure 4, rep-
resents the efficiency of gear number q. Constants m
−0.5 0 0.5 1 1.5 2
−0.5
0
0.5
1
1.5
x2
Values of g1 and g2
g1 g2
Figure 4: g
1
and g
2
behaviors
(mass of the car), c (frictional damping) and k (con-
stant of transmission shaft) are set to 1 without loss of
generality.
Optimization problem - Firstly, contrary to (Hed-
lund and Rantzer, 2002), we impose rules rather nat-
ural for the car evolution which are listed below:
[t
0
, t
1
[ [t
1
, t
2
[ [t
2
, t
3
[ [t
3
, t
4
[
[t
4
, t
5
[ [t
5
, t
6
[ [t
6
, t
7
[ [t
7
, t
8
[
Action accelerate accelerate brake brake
Gear 1
st
2
nd
2
nd
1
st
Here, we optimize switching and final times t
i
, i =
1, .., 8 to stop the car as near as possible of a first
chosen destination (x
1
= 0), then, after a new start-
up, to stop it as near as possible of a second chosen
destination (x
1
= 5) and this, in a minimum time.
4.2 Gradient Calculus. Criterion
Minimization
Following notations used in the second section and
particularly in equation (3), we can consider the aug-
mented criterion J =
P
N+1
i=1
J
i
, N = 7, with:
J
i
=
α
N + 1
(
x
2
δ
− v
g
i
)
2
+ ν
i
t
i
− a
i
N + 1
+
Z
t
i
t
i−1
(H
i
− λ
T
i
˙
X
i
)dt,
where:
• δ = 50: tolerable changing amplitude,
• v
g
i
= 0.8, i = 1, 5, v
g
i
= 1.2, i = 2, 6, v
g
i
= 0.2,
i = 3, 7, v
g
i
= 0, i = 4, 8: recommended changing
velocity,
• a
i
= t
i
, i = 1, .., 8,
• H
i
= L
i
+λ
T
i
f
i
where L
i
= β(x
2
1
(t)+x
2
2
(t)), i =
1, .., 4, L
i
= β((x
1
(t) − 5)
2
+ x
2
2
(t)), i = 5, .., 8
f
i
= AX
i
+ B, with:
∗ A =
0 1 0
0 −1 1
0 −1 0
!
,
∗ B =
0
0
ug
q
!
with u = 1.1 for i = 1, 2,
u = −0.1 for i = 3, 4, g
q
= g
1
for i = 1, 4,
g
q
= g
2
for i = 2, 3.
Then, like for the thermostat problem, we apply the
optimization algorithm related in section 2. Firstly,
we solve numerically direct system (9) to define
switching and final times and states. Then, we solve
adjoint system backwards given by (4) which is given
here by:
˙
λ
T
i
= −A
T
λ
T
i
− (2β(x
1
(t) − d) 2βx
2
(t) 0)
T
.
OPTIMAL CONTROL APPLIED TO OPTIMIZATION OF MOBILE SWITCHING SURFACES PART II :
APPLICATIONS
375

with t ∈ [t
i+1
, t
i
[, d = 0 for i = 1, .., 4, d = 5 for
i = 5, .., 8.
In the same time, we obtain suites ν
i
, λ
i
(t
i
) given by
(5) which, applied to the car problem for i = 8, .., 1
and considering (6), gives system:











ν
i
= −8(β((x
1
(t
i
) − d)
2
+ x
2
2
(t
i
)
−(x
1
(t
i+1
) − d
2
)
2
− x
2
2
(t
i+1
))
+λ
T
i+1
(f
i
− f
i+1
) + (0
α
4
(
x
2
(t
i
)
50
− v
g
i
) 0)f
i
),
λ
T
i
(t
i
) = λ
T
i+1
(t
i
) + (0
α
4
(
x
2
(t
i
)
50
− v
g
i
) 0),
where d = 0 for i = 1, .., 4, d = 5 for i = 5, .., 8,
d
2
= 0 for i = 1, .., 3 and d
2
= 5 for i = 4, .., 7.
Then, we deduce from (7):
dJ
0
i
da
i
= −
ν
i
8
, i = 1, .., 8,
which is the criterion gradient.
Thus, we apply a descent method to define an op-
timal solution. We use again Matlab and function
fmincon with initial values: α = β = 0.5, t
1
=
1.7, t
2
= 5.1, t
3
= 6.9, t
4
= 8, t
5
= 10.1,
t
6
= 12.8, t
7
= 14.1, t
8
= 15.4 . The algo-
rithm stops after thirteen iterations and gives the fol-
lowing optimal results: (t
1
, t
2
, t
3
, t
4
, t
5
, t
6
, t
7
, t
8
) =
(2.2597, 5.4952, 6.9851, 7.8253, 10.2369, 12.7535,
13.9783, 15.3068), J
0
= 203.1983. Figure 5 shows
car trajectory in the phase portrait of x
1
and x
2
.
−5 −4 −3 −2 −1 0 1 2 3 4 5 6
0
0.2
0.4
0.6
0.8
1
1.2
Car trajectory
Position
Velocity
Figure 5: Trajectories before (dotted line) and after (solid
line) optimization
Figure 5 confirms that our optimization algorithm en-
ables the car to approach desired destinations. Be-
yond the simplifying assumption about bang-bang
control u we have made, this algorithm is numeri-
cally less expensive than the one based on dynamic
programming used in (Hedlund and Rantzer, 2002).
5 OPTIMIZATION OF
SWITCHING RULES.
APPLICATION TO ROBOTICS
5.1 Studied Robot Model
Following (Boccadoro, 2004), we consider system
(10):



˙x = vcos(φ)
˙y = vsin(φ)
˙
φ = w
(10)
where (x, y) is the robot position, φ is its orientation,
v and w are the controlled translational and angular
velocities. Moreover, the robot can move using two
modes, an approach-goal one and an avoid-obstacle
one, which are respectively given by:
Mode 1

v = 1
w = C
1
(φ
g
− φ) with φ
g
= arctan(
y
g
−y
x
g
−x
)
Mode 2

v = 1
w = C
1
(φ − φ
o
) with φ
o
= arctan(
y
o
−y
x
o
−x
)
Point (x
g
, y
g
) defines the position of the target that
the robot has to reach and (x
o
, y
o
) defines the po-
sition of the obstacle that the robot has to avoid.
Here, contrary to (Wardi et al., 2004), we choose a
mobile obstacle which follows a circle of equation
(x
o
− 1)
2
+ (y
o
− 1)
2
− (0.3)
2
= 0.
The crossover between the two modes can be de-
scribed as follows. We define for each obstacle po-
sition two switching surfaces of equation:
Ψ(x, y, a
i
) = (x − x
o
)
2
+ (y − y
o
)
2
− a
2
i
, i = 1, 2.
Firstly, the robot operates in mode 1 until it crosses
a switching surface of radius a
1
and then, it switches
to mode 2. It remains in mode 2 until it crosses a
switching surface of radius a
2
and then, it goes back
to mode 1.
Optimization problem - How can we choose radii
a
1
and a
2
in order that the robot reaches the pre-
specified target without never meating the mobile ob-
stacle ?
5.2 Gradient Calculus. Criterion
Minimization
Following notations used in the algorithm reminder
and particularly in equation (3), we can consider the
augmented criterion J =
P
N+1
i=1
J
i
, N = 2, with:
J
i
= ν
i
[(x−x
o
)
2
+(y−y
o
)
2
−a
2
i
]+
Z
t
i
t
i−1
(H
i
−λ
T
i
˙
X
i
)dt,
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
376

where H
i
= L
i
+ λ
T
i
f
i
, with L
i
= (x − x
g
)
2
+ (y −
y
g
)
2
, f
i
= (vcos(φ(t
i
)) vsin(φ(t
i
)) w )
T
.
From there, we apply algorithm of section 2. Firstly,
we solve direct system (10) forwards. Secondly, we
solve adjoint system (4) backwards which is given
here by:
˙
λ
T
i
= −A
T
λ
T
i
− (−2(x
g
− x) − 2(y
g
− y) 0)
T
,
where, if the robot operates in mode 1:
A =



0 0 C
1
y
g
−y
(x
g
−x)
2
+(y
g
−y )
2
0 0 −C
1
x
g
−x
(x
g
−x)
2
+(y
g
−y )
2
−vsin(φ) vcos(φ) −C
1



and if the robot uses mode 2:
A =


0 0 −C
2
y
o
−y
(x
o
−x)
2
+(y
o
−y )
2
0 0 C
2
x
o
−x
(x
o
−x)
2
+(y
o
−y )
2
−vsin(φ) vcos(φ) C
2


.
In the same time, we compute ν
i
, λ
i
(t
i
), i = 3, .., 1
given by (5). Considering (6), we obtain:

















ν
i
= −((x(t
i
) − x
g
)
2
+ (y(t
i
) − y
g
)
2
−(x(t
i+1
) − x
g
)
2
− (y(t
i+1
) − y
g
)
2
+λ
T
i+1
(f
i
− f
i+1
))(2v(cos(φ(t
i
))(x(t
i
) − x
g
)
+sin(φ(t
i
))(y(t
i
) − y
g
)))
−1
λ
T
i
(t
i
) = λ
T
i+1
−2ν
3
((x
o
− x(t
3
)) (y
o
− y(t
3
)) 0).
Then, equation (7) yields:
dJ
0
i
da
i
= −2ν
i
a
i
,
which is the criterion gradient.
Thus, we apply a descent method to define an optimal
solution. We use again Matlab and we choose the fol-
lowing initial values: C
1
= 1.2, C
2
= 0.5, x
g
= 3,
y
g
= 2.5, a
1
= 0.85, a
2
= 1.05 . The algorithm stops
after nine iterations and gives the following optimal
results: (a
1
, a
2
) = (1.0724, 1.2724), J
0
= 39.8023.
Figures 6 and 7 show respectively Matlab simulations
before and after optimization. The robot is nearer of
the target after optimization than before. Crosses and
stars represent respectively switching times for the ro-
bot trajectory and for the obstacle trajectory. Lengths
of the solid circle archs measure trajectory durations.
They also illustrate the interest of our study compared
to (Boccadoro, 2004).
6 CONCLUSION
These three applications reinforce theorical results
obtained in (Jolly et al., 2005) and show all the diver-
sity of applications areas in which our optimization
algorithm can be useful.
0 0.5 1 1.5 2 2.5 3 3.5
0
0.5
1
1.5
2
2.5
3
target
Figure 6: Trajectory of the robot before optimization
0 0.5 1 1.5 2 2.5 3 3.5
0
0.5
1
1.5
2
2.5
3
target
Figure 7: Trajectory of the robot after optimization
REFERENCES
Boccadoro, M. (2004). Optimal Control of Switched
Systems with applications to Robotics and
Manufacturing. PhD thesis, Universit
`
a degli
Studi, Perugia, Italia.
C
´
ebron, B. (2000). Commande de syst
`
emes dynamiques hy-
brides. PhD thesis, Istia, Angers, France.
Cyssau, R. (1990). Manuel de la r
´
egulation et de la gestion
de l’
´
energie. Ass. Confort Regulation, Pyc edition.
Gapaillard, M. (2003). Optimal Control for a Class of
Hybrid System via a Stochastic Method. In Proceed-
ings of IEEE - ICCA. Montreal.
Hedlund, S. and Rantzer, A. (2002). Convex Dynamic
Programming for Hybrid Systems. In IEEE Trans-
actions on Automatic Control.
Jolly, J.-C., Qu
´
emard, C., and Ferrier, J.-L. (2005). Optimal
Control Using Parameterized Mobile Switching
Surfaces. Part 1: Algorithm. In ICINCO 2005.
Qu
´
emard, C., Jolly, J.-C., and Ferrier, J.-L. (2005). Search
for Cycles in Piecewise Linear Hybrid Dynamical
Systems with Autonomous Switchings. Application
to a Thermal Device. In IMACS’2005 World
Congress.
Wardi, Y., Egerstedt, M., Boccadoro, M., and Verriest, E.
(2004). Optimal Control of Switching Surfaces. In
CDC’2004.
OPTIMAL CONTROL APPLIED TO OPTIMIZATION OF MOBILE SWITCHING SURFACES PART II :
APPLICATIONS
377