SELF-LEARNING DISTURBANCE COMPENSATION FOR ACTIVE

SUSPENSION SYSTEMS

Eckehard M

unch, Henner V

ocking, Thorsten Hestermeyer

University of Paderborn

Pohlweg 98, D - 33098 Paderborn

Keywords:

mechatronics, learning, distributed optimization, active suspension, railway systems.

Abstract:

Ride comfort and safety of vehicles can be increased by active suspension systems. A problem is the detection

of disturbances which can generally not be measured until they impact the chassis. Provided guidance and

disturbance are known in advance, a controller can use this information to achieve considerably improved

behavior. This paper presents an approach in which railway vehicles coupled in a network, in repeated runs

over the same track section, learn a disturbance compensation that can almost entirely compensate for sta-

tionary disturbances, i.e., disturbances that occur at the same spot in equal measure. Here information on the

respective track section is sampled, stored locally at the track, and retrieved by the succeeding vehicle which

will use them for an improved compensation for the occurring disturbances and again store information there.

This iterative procedure results in an optimal compensation.

The algorithm is described and criteria for its design are derived from digital control theory. The procedure was

implemented on a testbed for a semi-vehicle with three degrees of freedom. The results of the measurements

are displayed and evaluated in this paper.

1 INTRODUCTION

Today, active suspension systems are well established

in theory and practice. This holds especially true for

automotive applications. When looking at the railway

industry, vehicles with active suspension are avail-

able, but these systems usually focus on tilt and cen-

tering of the coach body rather than on ride comfort.

However - even if rare - , there has also been some

work on active damping in industry (Streiter et al.,

2001) and public research. This work uses as applica-

tion example the system setup of the railway system

”Neue Bahntechnik Paderborn”, which is explained

in more detail in section 2.

Most of the vast number of literature on the control

of active suspension systems focuses on single vehi-

cles. Collaborative vehicle networks, however, offer

a promising way to improve ride comfort even fur-

ther: This paper shows, that it is possible to reduce

the body motion by a great extent by using the expe-

rience gained by other vehicles. In order to do so, two

things are necessary: First, an algorithm is required,

that determines information about the track excitation

and uses this in the control algorithm of the active sus-

pension. Second, a collaborative network with com-

munication infrastructure has to be set up. This paper

focuses on the ﬁrst step.

The paper is structured as follows:

Section 2 presents the basic idea for the overall sys-

tem setup in the collaborative vehicle network. With

this setup in mind, section 3 describes an example

suspension system and the control structure including

a learning algorithm. Section 4 develops this learning

algorithm. In order to show the applicability of the al-

gorithm and its beneﬁts, the system was implemented

on a suspension test rick described in section 5. Sec-

tion 6 discusses the results. The paper concludes with

an outlook in section 7.

2 PREVIEW SYSTEMS FOR

ACTIVE SUSPENSIONS

When designing an active suspension it is important

to put special care on the employed sensor concept

and the control strategy as both play a mayor role

in the success of the system. One important aspect

became clear already with ﬁrst realizations of active

suspension systems: Disturbance compensation using

Münch E., Vöcking H. and Hestermeyer T. (2005).

SELF-LEARNING DISTURBANCE COMPENSATION FOR ACTIVE SUSPENSION SYSTEMS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 32-38

DOI: 10.5220/0001185700320038

 SciTePress

information about the ground excitation can improve

the ride comfort considerably. (J

aker, 1990) e.g. used

a disturbance compensator as part of the control law

for the active suspension in an off-road truck with

great success

The way in which the ground excitation is deter-

mined has signiﬁcant inﬂuence on the compensation

result. Due to actuator dynamics it is vital to know

the ground excitation as early as possible. In the

optimal case the excitation is known before it actually

hits a wheel. This is known as ”preview”. Preview

information for the rear wheels can be gained by

using information from the front wheels (so called

”internal preview”). This is quite a convenient way

for disturbance compensation in trains, where the

locomotive can collect track information and transfer

it to the carriages. In short vehicles like cars however,

the inﬂuence of the front wheels on comfort is

very high and internal preview provides only small

beneﬁt (Rutz, 1987). Preview information for the

front wheels would therefore help to improve ride

comfort even more. Unfortunately, looking at a single

vehicle, collecting preview information for the front

wheels is an arduous and costly business.

A much

simpler way to obtain the desired information can be

found for vehicles integrated in a network. (Ioannou,

1998) proposes such an infrastructure supported

network for highway vehicles. This paper focuses on

the railway system ”Neue Bahntechnik Paderborn”

(NBP) (Hestermeyer, 2003), which supplies a perfect

infrastructure for the new preview system presented

here:

The railway system NBP features small au-

tonomous railway vehicles of van size with a fully-

active suspension system. The shuttles are propelled

by a double- fed asynchronous linear motor. For the

implementation of the motor, the track is divided into

sectors, which are equipped with their own computer

hardware. The creation of the propelling forces re-

quires fast communication between the shuttles and

the track. Fig. 1 shows the information and commu-

nication structure of the NBP-system (Zanella et al.,

2002). The available computation power and commu-

nication infrastructure can be used to set up a preview

system for the active suspension (Hestermeyer et al.,

2004; M

unch et al., 2004).

The system structure shown in Fig. 1 suggests the

following set-up for the determination of the track

excitation:

Information about the wheel excitation was derived

from an observer based on signals from accelerometers

mounted on the axles.

(Donahue, 2001) e.g. describes a military external pre-

view system with expensive radar and optical sensors.

Track

ControlCenter

FC FC FC FC FC FC FC FC

SectorControl SectorControl

MainControlCenter

Communication

SectorControl

FrequencyConverter

&LocalControl

Figure 1: Communication structure for the railway-system

”Neue Bahntechnik Paderborn” (Zanella et al., 2002)

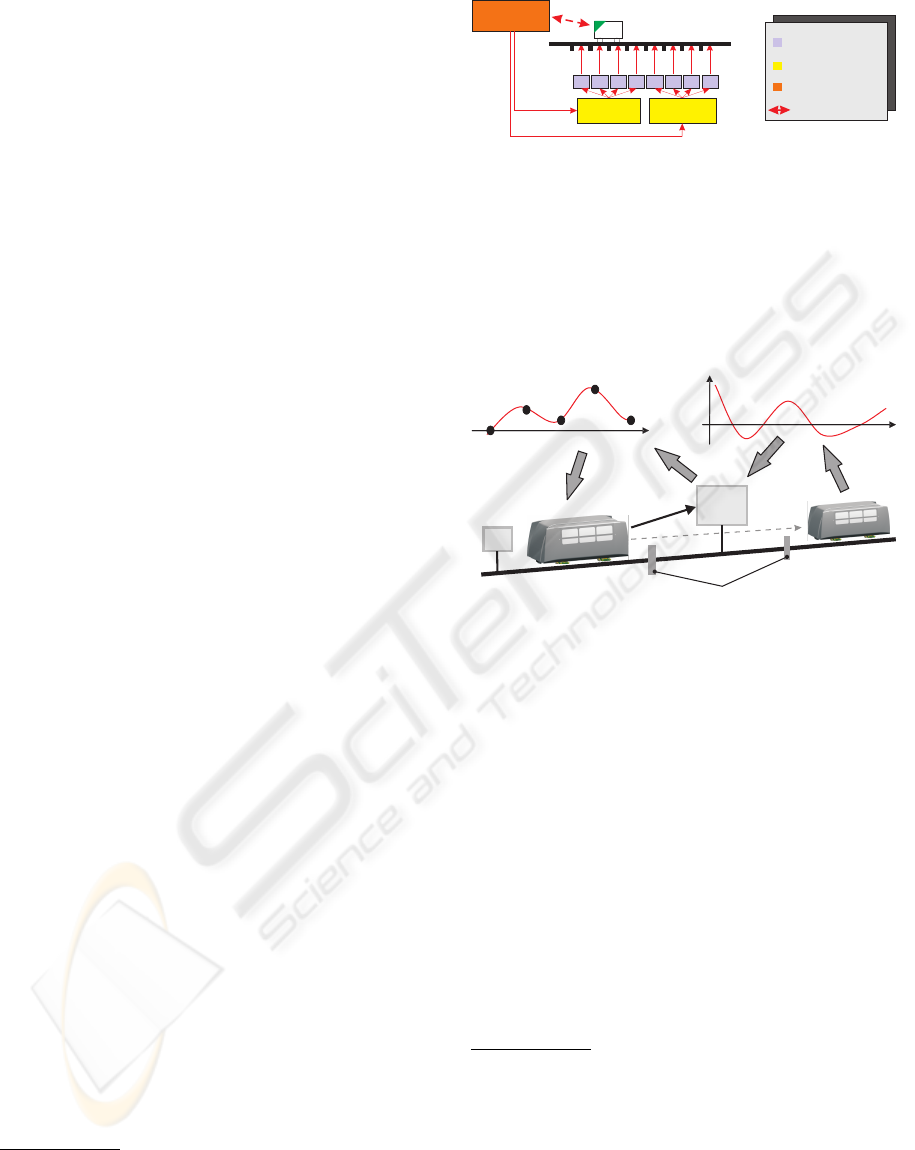
In a ﬁrst step, the track is logically devided into

different sections and an agent network is allocated to

the track. One track agent is allocated to each section

(Fig. 2).

track

agent

excitationtrajectories

comfortmeasurement

incoming

shuttle

outgoing

shuttle

sectionboundaries

Figure 2: Determination of preview information by multi-

agent optimization

When a shuttle wants to enter a special section, it

contacts the track agent and receives in return an es-

timation of the track excitation it can use for distur-

bance compensation

After completing the section the

shuttle answers with a performance rating, which is

used by the track agent to optimize the trajectory. In

case of a communication error, disturbance compen-

sation is simply turned off. This results in less com-

fort but is otherwise uncritical.

Next to the beneﬁt of improving ride comfort by

optimal disturbance compensation, this method of-

fers an excellent way of monitoring the track quality,

as the track information is continously updated with

each shuttle. Special measurement runs can be re-

duced or maybe even totally stopped.

Comparing Fig. 1 and 2 it seems obvious to select the

sections according to the motor sectors and download the

track agent software on the available sector hardware. How-

ever, this is not a prerequisite. The multi-agent software can

also be run on centralised hardware.

The dynamics of the respective shuttle has to be con-

sidered when using the preview information. Otherwise the

optimization of the preview information in the track agent

might yet converge, but is now valid only for shuttles with

similar dynamics.

SELF-LEARNING DISTURBANCE COMPENSATION FOR ACTIVE SUSPENSION SYSTEMS

3 ACTIVE SUSPENSION

CONTROL

Suspension System Before discussing the en-

visioned control system in more detail, it is ﬁrst

necessary to have a look at the physics of the re-

garded active suspension system (ﬁg 3): Car body

and bogie are connected by air springs. The function

of passive dampers is taken on by an active system

of hydraulic cylinders that creates damping forces by

displacing the spring bases. The displacement vector

disp

yields the necessary cylinder displacements

cyl,i

by computing the inverse kinematics of the

cylinder arrangement.

undercarriage

suspensionframe

carbody

suspensioncylinder

airspring

Figure 3: Structure of active suspension

Control Structure As already mentioned in the in-

troduction, this paper focuses on the realization of

the disturbance compensation and the trajectory opti-

mization of the distributed control system envisioned

in section 2. Communication issues and questions

arising from the multi-agent implementation are dis-

regarded. Fig. 4 shows the structure of the self-

learning control system including the learning algo-

rithm.

controller

inverse

kinematics

plant

learning

algorithm

objective

generation

obj

active

disp

cyl

Figure 4: Structure of learning algorithm

The basis of the active suspension control is a sim-

ple feedback law (block ”controller”) assuring sufﬁ-

cient damping of the car body. The control law uses

the relative position y between body and bogie to

compute the necessary displacement x

active

In order to minimize the absolute movement of the car

body, an additional relative displacement signal f is

introduced, which includes reference and disturbance

information in dependance of the shuttle position s

(Hestermeyer et al., 2004). The table

f = (s

, f

) de-

termines f from s by interpolation.

Based on the system response,evaluated by the block

objective generation, a superposed learning algorithm

computes a trajectory that reduces the inﬂuence of

disturbances in the track by adding the signal f to the

relative displacement between body and bogie.

Section 2 suggested the usage of the track exci-

tation as disturbance compensation. This requires

knowledge of vehicle and actuator dynamics when

using the excitation trajectory in the controller. In a

ﬁrst step, this dynamics was not explicitly considered

in this paper, so that car body and actuator dynamics

were reﬂected in the determined trajectories.

4 LEARNING ALGORITHM

During the run over a track section different distur-

bances affect the chassis of a shuttle. These dis-

turbances can be distinguished into stochastic distur-

bances and stationary disturbances, which recur at the

same place of the track section. The learning algo-

rithm presented here identiﬁes and compensates these

stationary disturbances on the chassis. The objective

here is to keep the car body of the shuttle as still as

possible, in order to improve the comfort of passen-

gers.

As described in section 3 the learning algorithm de-

termines a trajectory as a sequence of numbers f

. k

indicates the step number of the learning process and

thus the number of shuttles that have crossed the sec-

tion.

The shuttle measures the movements of the car

body during the passage over the track section. After-

wards the data is given back to the learning algorithm,

which determines the new sequence f

k+1

Learning Algorithm As learning algorithm a com-

putation instruction of the form

k+1

= f

− K

· y

(1)

with

j = i + h (2)

was chosen. The value K

gives the learning factor

of the algorithm and y

the deviation of the car body

position. The value h reﬂects the dynamics of the car

body and indicates a shift of the f

signal compared

to the associated measuring point. This shift is cho-

sen according to the cut-off frequency of the car body

dynamics T and the travel speed of shuttle v.

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

For the passage over the regarded track section a

constant speed

v(t) = const. (3)

is assumed.

Convergence Analysis The learning algorithm in

equation (1) has great similarities to the description of

discrete controllers. They differ in the meaning of the

counting variable k, which describes the progressing

of the time with discrete controllers. In the learning

algorithm presented in this paper the variable k indi-

cates a new run over the respective track section.

It is obvious to analyze the convergence char-

acteristics of the learning algorithm by means of

well-established digital control-engineering methods

(Hanselmann, 1984). Therfore it is necessary to de-

scribe the shuttle-dynamics by a mathematic model.

In order to treat the supporting points independently

from each other, some simpliﬁcations must be made

for the convergence analysis of the learning algo-

rithm. For the feed-forward signal a simple step-

function in place of the interpolation function is used.

Furthermore an ideal reference reaction of the car

body is assumed. The system response of the shut-

tle can be described with the simple model

= K



+ u



(4)

in which u

describes the track disturbance at the sup-

porting point i.

Inserting into the learning algorithm equation (1)

yields

k+1

= f

− K

· K



+ u



(5)

The use of the Z-transformation with equation (5)

results in the transfer function:

G(z) =

(z)

· K

1 − K

· K

− z

(6)

In order to analyze the stability of the system, the

poles of (6) can be used.

z = 1 − K

· K

(7)

For a stable system behavior the pole stays within the

unit circle.

0 < K

· K

< 2 (8)

In the stability analysis presented above strong sim-

pliﬁcations were made. The dynamic behavior of

the shuttle was reduced to a simple gain factor K

whereby the dependencies between neighbored sup-

porting points were eliminated. If one selects this gain

to be the overshoot of the car body response to

a unit step, then one receives a useful estimation for

the feasible range of the learning factor K

. In prac-

tice the convergence will be assured by reducing the

learning factor to a relative small value. On the one

hand this leads to a decreased learning speed, on the

other hand the insensitivity of the feed-forward signal

to the above mentioned stochastic disturbance is

increased.

5 REALISATION

For a test in practice, the approach for a preview con-

trol presented here was realised in a simpliﬁed envi-

ronment. In the following, we will expound the con-

ﬁguration of the testbed and present the implementa-

tion of the procedure described.

Conﬁguration of the Testbed The control of the

damperless suspension/tilt system is described in

(Hestermeyer et al., 2003) for the complete vehicle.

To test the active suspension of the entire vehicle a

testbed was built up in the context of the ”Neue Bah-

ntechnik Paderborn”. This testbed allowed us to de-

sign and test the suspension control (Liu-Henke et al.,

2002). Fig. 5 shows the testbed. Three lower hy-

draulic cylinders serve to simulate track excitations

and are able to impose forces resp. torques in horizon-

tal, vertical, and rotatory directions on the car body.

The upper part represents the suspension/tilt module

as it might be mounted aboard the vehicle. The mass

of the carriage is supported exclusively by airsprings,

as described in section 3.

Figure 5: Suspension-tilt testbed

With the procedure described here a control of the

relative motion between chassis and carriage body is

sufﬁcient. In order to achieve an increase in comfort

one might think of damping the absolute motions of

the carriage body

, but this was not included in the

present control because the absolute motions are to

be impacted by the preview algorithm.

Implementation of the Learning Algorithm In or-

der to test the self-optimisation approach presented in

section 4 at the testbed we needed a recurring exci-

tation for a simulation of repeated rides along a ﬁxed

section. For this purpose a track course was deﬁned

that stretched over a 100-m-long track section. For

This method known as ”skyhook damping” (Hester-

meyer et al., 2004)

SELF-LEARNING DISTURBANCE COMPENSATION FOR ACTIVE SUSPENSION SYSTEMS

determining the objective variables we subdivided the

track section into 100 parts of 1 m each; thus for any

possible moving direction an evaluation vector com-

prising 100 elements was recorded for each crossing.

For an objective we used the maximum of deviations

from the middle position of the car body in the respec-

tive part; it was measured by the existing position-

measuring sensors. One run over the track section in

view takes 10s at an assumed speed v = 10m/s. Af-

ter each crossing the evaluation vectors are transmit-

ted to the learning algorithm which deﬁnes the new

trajectories of the disturbance compensation for the

next crossing. These trajectories are parameterised

over 100 supporting points corresponding to the sec-

tions. As shown in ﬁg. 4 the signal f is interpo-

lated between the supporting points. The algorithm

required to determine an optimal disturbance com-

pensation was implemented on a dSPACE real- time

hardware, in addition to the testbed control described.

Here the focus was on testing the learning algorithm.

Difﬁculties resulting from the necessary communica-

tion between vehicle and processing of information

on the track were ignored here. At the time interval

where the crossing is ﬁnished the detected evaluation

variables are transmitted to the optimising procedure

which then computes the new trajectories of the dis-

turbance compensation at exactly the same time in-

terval and makes them available for the next crossing

that begins at the next time interval.

6 RESULTS

This section describes the results of the optimisation

on the basis of measurements at the testbed. The re-

curring excitation over the track section in question is

displayed in Fig. 6 to 8 at the top. In translatory di-

rection the chassis was at ﬁrst excited by a sinusoidal

signal and subsequently by three steps in lateral direc-

tion resp. inversely in vertical direction. Additionally

a superposed sinusoidal rotation around the longitu-

dinal axis of the chassis took effect. The middle dia-

grams display the disturbance trajectory acquired by

repeated runs in the course of optimisation. The plot

shows the characteristics as follows: at the outset of

the optimisation as a dotted line, after ﬁve crossings as

a broken one, and as an unbroken line after 50 cross-

ings. The lower part displays the corresponding plots

of the evaluation functions.

All in all the optimisation method has proved its

ability to compensate the car body movements almost

in full for the periodically recurring excitations. After

only ﬁve crossings the amplitudes of the body motion

fell below 10%. After 50 crossings the carriage body

is nearly in a position of rest in spite of the excitation.

Another aspect is made clear in a comparison of

the excitation behaviors and the corresponding dis-

turbance compensation. With a vertical motion these

variables converge while with torsion and lateral mo-

tion there remain signiﬁcant differences even after 50

repetitions. This is due to the coupling of motions.

A lateral excitation will always bring about a torsion

in the car body; vice versa, a rotation of the chas-

sis around the longitudinal axis will always affect the

lateral motion of the car body. This is why the dis-

turbance compensation has to take into account these

couplings, the result being the behavior shown. On

the other hand, the car body motion in vertical direc-

tion is decoupled from the other degrees of freedom;

thus the disturbance compensation will only have to

deal with the excitation portion in this direction.

7 CONCLUSION

It was shown that using existing data processing in-

frastructure for the exchange of collected data can be

effective for the compensation of recurring stationary

disturbances. The realization at the testbed conﬁrmed

the advantages of this approach. However it may not

be ignored that the trajectories of the compensation

do not represent the disturbances themselves. Rather

they are optimized with respect to the particularly re-

garded vehicle and its velocity. At the testbed this

causes no problem, because the dynamics and the as-

sumed velocity of the testbed does not change during

a test. Of course in reality different vehicles must be

considered. In this case the compensation adapted to

a particular vehicle cannot be used. In order to be able

to use the presented method nevertheless, vehicle and

velocity independent information must be stored. For

this purpose the actual track characteristics are ideal

which can be determined by observation from the re-

spective system response of an individual vehicle. In

this way the approach introduced here can be gener-

alized on different types of vehicles.

Thus the method represents a good way to improve

the dynamic behavior for repetitive motions. It can

also be transferred to other applications, which show

similar characteristics.

To prove the convergence of the learning algorithm

a simpliﬁed convergence analysis was performed by

using methods derived from digital control theory.

An enlargement of the convergence model in view of

a concurrent analysis of several supporting points is

possible and will be object of future research.

REFERENCES

Donahue, M. D. (2001). Implementation of an active sus-

pension, preview controller for improved ride com-

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

fort. Master’s thesis, The University at Berkeley.

Hanselmann, H. (1984). Diskretisierung kontinuierlicher

regler. Regelungstechnik, 32(10).

Hestermeyer, T. (2003). railcab - an integrative system

for the 21st century. Urban Tranport International,

(50):24–25.

Hestermeyer, T., Ettingshausen, C., and Schlautmann, P.

(2003). Aktive Federung f

ur Schienenfahrzeuge - Sys-

temaufbau, Regelung und Realisierung. In 5. VDI-

Mechatroniktagung, Fulda, Germany.

Hestermeyer, T., M

unch, E., and Oberschelp, O. (2004).

Sollbahn-Planung f

ur schienengebundene Fahrzeuge.

In Numerical Analysis and Simulation in Vehicle

Engineering, VDI-Berichte 1846, pages 137–158,

urzburg.

Ioannou, P. (1998). Evaluation and analysis of automated

highway system concepts and architectures. Cali-

fornia PATH Research Report UCB-ITS-PRR-98-12,

University of Southern California.

aker, K.-P. (1990). Entwicklung realisierbarer hi-

erarchischer Kompensatorstrukturen f

ur lineare

Mehrgr

oßensysteme mittels CAD. Number 243 in

VDI-Fortschritt-Berichte, Reihe 8. D

usseldorf.

Liu-Henke, X., L

uckel, J., and J

aker, K.-P. (2002). An ac-

tive suspension/tilt system for a mechatronic railway

carriage. Journal of IFAC, Control Engineering Prac-

tice, (10):991–998.

unch, E., Hestermeyer, T., Oberschelp, O., Scheideler,

P., and Schmidt, A. (2004). Distributed optimization

of reference trajectories for active suspension with

multi-agent systems. In European Simulation Mul-

ticonference 2004 - Networked Simulations and Sim-

ulated Networks, pages 343–350, Magdeburg, Ger-

many. SCS.

Rutz, R. (1987). Entwurf eines komplexen

Mehrgr

ossenreglers f

ur die aktive Federung eines

gel

andeg

angigen Nutzfahrzeuges. Master’s thesis,

MLaP, University of Paderborn.

Streiter, R., Boller, M., Riege, B., Schneider, R., and Him-

melstein, G. (2001). Active lateral suspension for high

speed trains - a step towards the mechatronic bogie. In

World Congress on Railway Research, Cologne, Ger-

many.

Zanella, M., Lehmann, T., Hestermeyer, T., and Pot-

tharst, A. (2002). Deterministic and high-performance

communication system for the distributed control of

mechatronic systems using the ieee1394a. In World

Computer Congress, Stream 7, DIPES, Montreal.

0 50 100

−0.01

0.01

excit

[m]

0 50 100

−0.02

0.02

comp

[m]

0 50 100

−0.02

−0.01

0.01

0.02

0.03

s [m]

obj

[m]

Figure 6: Evaluation: lateral

0 50 100

−0.01

0.01

excit

[m]

0 50 100

−0.02

0.02

comp

[m]

0 50 100

−0.02

−0.01

0.01

0.02

s [m]

obj

[m]

Figure 7: Evaluation: vertical

SELF-LEARNING DISTURBANCE COMPENSATION FOR ACTIVE SUSPENSION SYSTEMS

0 50 100

−0.02

0.02

excit

alpha

[rad]

0 50 100

−0.05

0.05

comp

alpha

[rad]

0 50 100

−0.03

−0.02

−0.01

0.01

0.02

0.03

s [m]

obj

alpha

[rad]

Figure 8: Evaluation: rotatory

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION