ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH

BASED ON LOCAL COMMUNICATION AND SENSING

Damien Bright

KnowledgeLab, University of Southern Denmark

Campusvej 55, DK-5230 Odense M, Denmark

Keywords:

simulation, collective robotics, stigmergy, reinforced random walk, optimization.

Abstract:

This paper presents a simulation model for experimenting with locally adaptive movement strategies for robots

involved in collective robotic search tasks in rapidly changing and uncertain environments. The model assumes

that the nature of the environment restricts inter-robot communication and uses a form of stigmergy based

local communication which has been widely applied in collective robots. The model is based on a biased

random walk where the degree of bias is linked to a local control variable which can change depending on

the evaluation of local adaption strategies. The local adaption strategies use an approach based on activation

functions to control the choice of which candidate paths should be inhibited or have increased preference over

random motion. Experiments aim to test the effectiveness of this approach for optimal collective search in

various test domains. A series of initial experiments is presented demontrating aspects of the model.

1 INTRODUCTION

Studies of foraging behaviour in insects and animals

have been used by many researchers in collective ro-

botics as a model for experimenting with search be-

haviour for robots (eg (Balch and Arkin, 1994)). The

modeling of foraging can be divided at a general level

into macroscopic or microscopic approaches where

the former is used to model the actions of large num-

bers of entities and the latter the actions of individ-

uals. It has been found that there are advantages in

the use of microscopic models with a high degree

of localization and the use of external communica-

tion mechanisms in improving the ability of collabo-

rating robots ((Holland and Melhuish, 1999), (Wag-

ner et al., 1999),(Montgomery and Randall, 2002))

to perform foraging or search type tasks. This is of-

ten because robots generally have independent control

software and it is advantageous to remove the need

to maintain direct communication and shared knowl-

edge of individuals exact locations between multiple

robots which can be difﬁcult to support in uncertain

and highly dynamic (i.e. rapidly changing) environ-

ments.

External communication mechanisms have at-

tracted considerable interest from collective robotics

and AI life researchers. In particular, the concept of

stigmergy (Holland and Melhuish, 1999) which de-

scribes a form of indirect communication utilizing the

environment as the communication medium has been

widely studied. Stigmergeric cues or markers rep-

resent a change made to the environment that com-

municates information and can take many forms E.g.

this could involve the use of beacons to guide robots

for tasks such as robot search and rescue. A much

studied form of stigmergeric marker is the use of

pheromone for trail marking where a chemical marker

(pheromone) is deposited. Entities in the system have

a pre-disposition to follow the strongest pheromone

trails they encounter and pheromone trails evaporate

(decay) over time which is useful for optimization.

Usually pheromone is considered as an attractant but

(Montgomery and Randall, 2002) has introduced the

concept of anti-pheromone as a useful tool for explor-

ing a search space. This is related to the fact that

a useful pure reactive strategy for search is to avoid

previously covered terrain which can be marked with

negative bias in the form of anti-pheromone.

Recent research in areas such as adaptive control

and optimization methods has examined the idea of

locally adaptive strategy within some search space.

For example this approach has been used in Genetic

algorithm (GA) work e.g. see (Igel et al., 2005) and

”self-tuning” methods for robotic control (Patterson

335

Bright D. (2005).

ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH BASED ON LOCAL COMMUNICATION AND SENSING.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 335-340

DOI: 10.5220/0001186503350340

 SciTePress

and Kautz, 2001). A large body of past research in

general optimization techniques such as gradient de-

scent and simulated annealing (Glover and Kochen-

berger, 2003) has also shown that the inclusion of ran-

dom processes can be important to achieving global

maxima/minima over local maxima/minima. Ro-

botic control which is purely reactive (like gradi-

ent following) can lead to the same type of local

maxmima/minima issues. The addition of random-

ness or noise into robotic motion has been shown to

help to avoid this (Balch and Arkin, 1994) but the

strategy used to determine the amount of random mo-

tion is generally ﬁxed (ie not locally adaptive) and

therefore not well suited to time-dependent problems

requiring adaption to changing or uncertain environ-

mental conditions.

The main contribution of this paper is the devel-

opment of a simulation model based on a novel ap-

proach for representing local self-tuning or adaption

strategies within the context of optimization of multi-

robot search in complex and dynamic domains. A key

aim of the simulation model is to be able to study

in detail the use and effect of local strategies which

vary the degree to which reactive behaviour to marker

trails and reinforcement of marker trails should dom-

inate over random motions. The random walk model

used in this paper can be compared to a markov de-

cision process and has inﬂuences from reinforcement

learning theory (Kaelbling et al., 1994). This paper is

structured as follows: First a brief summary is given

of related work, then the numerical model is deﬁned

and a set of initial results is presented. A summary

and future work section then describes some of the

aims and proposed uses of the simulation model.

2 RELATED WORK

A large body of research in AI life applied to opti-

mization and guidance problems has made use of in-

direct communication techniques based on social in-

sects such as trail laying. This has led to the term

synthetic pheromone describing data structures in-

spired by chemical markers called pheromones from

biological systems. Research in collective robotics

(Holland and Melhuish, 1999) has made substantial

use of stigmergy and other concepts from AI life re-

search. Approaches based on such techniques can

a provide robust and adaptive indirect coordination

mechanism for collaborating entities such as robots

(Wagner et al., 1999). Multiple robots using such

techniques are particularly efﬁcient for tasks such

as mapping unknown terrain which are well suited

to being performed collectively. Each robot needs

only relatively simple functionality to achieve com-

plex group behaviour. This reduces the complexity

and cost of each robot. Different approaches to navi-

gation strategy for indoor searching have been exam-

ined by (Gonzales-Banos and Latombe, 2002). One

approach to aid search behaviour has been the use of

coverage maps (Stachniss and Burgard, 2003) which

in a similar way to maker trails can be viewed as a

form of indirect communication stored in the environ-

ment. Lately there has been increased use of multi-

ple robots to perform specialized tasks (eg search and

rescue (Baltes and Anderson, 2003)). Some common

problems with multiple robot guidance are:

(1) Pure reactive navigation often suffers from local

minima issues due to limitations such as sensor range

and/or accuracy. It has been found that a combina-

tion of goal directed behaviour and reactive behaviour

can be an effective (Balch and Arkin, 1994) strategy

but this often requires more complex robot behaviour

such as the use of path planning algorithms.

(2) centralized versus de-centralized control and

whether to use localized and indirect communica-

tion. Decentralized control and indirect communi-

cation (see (Holland and Melhuish, 1999), (Wagner

et al., 1999)) can be very useful in complex and dy-

namic environments where the environment is spa-

tially/geographically complex or where the positions

of objects that exist in the environment change or the

environment itself is subject to uncertainty or change.

Also robots with limited ability to transmit and com-

municate over longer distances can beneﬁt from an

approach based on local communication.

Random walk models have been widely used to

model movement patterns such as dispersion. It is

possible under certain conditions to look at local con-

trol decisions in a biased random walk as a form of

Markov decision process. (Azar et al., 1992) examine

optimal strategy applicable to time independent long

term behaviour of a random walk on a ﬁnite graph

where local movement decisions can be viewed in

terms of a controller selecting from a set of available

actions to bias the behaviour of a markov chain. This

type of approach has relevance for this paper but is not

able to address time dependent local strategy forma-

tion. A reinforced random walk model was ﬁrst pro-

posed by Coppersmith and Diasconis (Coppersmith

and Diaconis, 1987) as way of modeling a person ex-

ploring a new city (See also (Davis, 1990)). Ran-

dom walk models can be used as an important part

of more speciﬁc models for spatial exploration and

cooperative interaction. For example a biased ran-

dom walk model which uses feedback with the en-

vironment to inﬂuence a walkers movement is the ac-

tive walker model originally formulated by (Lam and

Pochy, 1993).

ICINCO 2005 - ROBOTICS AND AUTOMATION

336

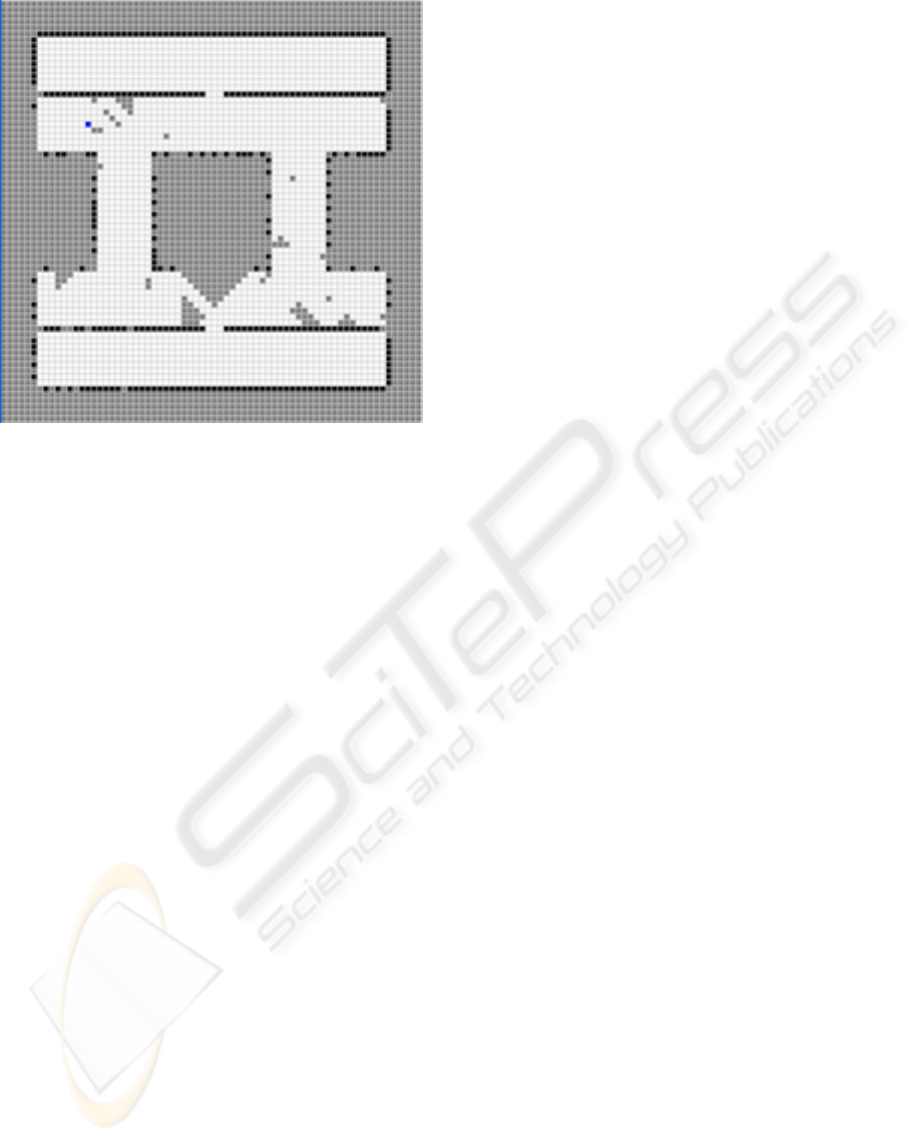
Figure 1: Single robot search on box canyon maze domain

with n

= 70, n

= 70, r

seed

= 2392093, R

= 0.0, and

ν = 0.95, nsteps = 5000, Starting position is (55, 35).

No strategy change is applied for this run.

3 NUMERICAL MODEL

The discrete time simulation model that is proposed

here is based on the mapping of values from a global

time dependent ﬁeld m(x, y, t), which represents the

dynamic (changing) part of the environment. m is

used to store data for stigmergy style collective com-

munication and gives the value of a marker (ie a type

of synthetic pheromone) m at position (x, y) in a 2D

domain at time t. m is mapped to local vectors of

the form v

, i = 0..N which represent the probabil-

ity of making one of N possible local choices (eg a

local control decision of picking an adjacent square

to move to) for robot j in the system on the next

timestep. Marker values m can be positive or neg-

ative representing an attractant marker or repulsant

marker respectively. The ﬁeld m(x, y, t) inﬂuences

the movement of robots in the system but also changes

due to feedback affects from individual robots when

an robot changes its local environment by laying a

marker trail. Therefore the model represents a stig-

mergy based form of indirect communication between

robots using the environment as the communication

medium.

Locally visible values of m(x, y, t) can be viewed

as positive or negative weights applied to local robot

decisions. The default trail laying behaviour of a ro-

bot is to deposit an initial positive concentration (rep-

resented by a value) of a marker at the grid square

(with position (x, y)) it occupies at each timestep.

This initial value is represented in the model as a

value m with initial magnitude 1.0. The model also

supports a robot laying a negative pheromone trail in

which case the initial value of m would be −1.0. This

means that unreinforced marker will be represented as

a m value in the range [−1.0, 1.0]. The concentration

of a marker can be reinforced by a grid square being

visited multiple times with the result that the mag-

nitude of reinforced m can increase without bound

over time. The magnitude of the marker can also be

made to decay over time by specifying a decay rate

which is applied to all squares containing a value

of m at each timestep. Robots can also have vari-

able sensor range limitations. In this model the sen-

sor range along a straight line path is represented as a

scalar value R

sense

which is measured in terms of a

number of grid cells.

3.1 Domain speciﬁcation

Domain boundaries and objects in the domain can be

represented in two ways in the model. There is a sta-

tic 2D function f(x, y) which can be used to deﬁne

locations (x, y) which block movement. These can

be used to represent objects in the domain where it

is assumed that the grid cells have a binary structure

(occupied or free). Global values from this function

are mapped to a local ﬁlter vector f

, i = 0..N which

has values of 0 or 1 and can be used to ﬁlter the avail-

able local choices. An robot cannot choose squares

that have been ﬁltered out and this can be used to set

up rigid type boundary conditions.

Alternatively a type of reﬂective boundary condi-

tion can be set up by specifying sufﬁciently large neg-

ative and non-decaying values of m(x, y, t). In this

case the boundary value at a square acts as a repulsive

force on robots in the system in such a way that an ro-

bot will tend to move away in the opposite direction.

Combining these methods provide a ﬂexible way to

specify complex domains and domain objects.

3.2 Local mappings

There are two important types of mapping that are

used in the model. First local vectors v

of the general

form:

, i = 0..N (1)

are used. Each v

represents a value related to the

probability of making choice i. The range of i rep-

resents the available number of local choices. In a

square type domain grid this can be used as part of

making a movement decision to one of 8 possible ad-

jacent squares (also known as a Moore neighborhood)

so in this case N = 7 in 1. All the results presented

in this paper use N = 7.

A superposition of vectors of type v

can be used

to combine a number of different effects that may in-

ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH BASED ON LOCAL COMMUNICATION

AND SENSING

337

ﬂuence a movement decision (see main equations be-

low) of an robot. This is a ﬂexible way to incorpo-

rate many factors that may inﬂuence decisions in the

model. Because many of the factors that can inﬂu-

ence movement decisions are related to the state of

the environment it is necessary to extract global val-

ues from m(x, y, t) or f (x, y) for the (N + 1) local

squares visible by an individual robot in the system at

each timestep. This is the ﬁrst type of mapping used

(global to local).

The other type of mapping relates to negative val-

ues of m(x, y, t). Because the value of v

repre-

sents a probability value it should be greater than

zero. Therefore there needs to be a way to map neg-

ative values of m(x, y, t) (which represent negative

weights) to a positive probability value. Since values

of m(x, y, t) are used to inﬂuence robot movement in

our model it has been chosen to map a negative value

of m(x, y, t) to a positive value of the same magni-

tude but in the opposite direction. This means a re-

pulsive effect on an robot movement decision is made

equivalent to an attractive effect in the opposite direc-

tion.

3.3 Main update equations

First we need to deﬁne a set of local vectors. A deci-

sion vector d

represents the ﬁnal probabilities of an

robot moving in one of i possible directions; a weight

vector w

represents weight values assigned to each of

the i possible path choices which are locally visible to

an robot and which represents an estimate of the max-

imum gain associated with choosing to move along a

particular path; a random decision vector r

represents

pure random choice (ie equal values for all i direc-

tions); a reinforcement decision vector l

represents

locally visible values of the component of m(x, y, t)

due to reinforcement; and a ﬁlter vector f

represents

a mask on which of the i choices are allowed or not

allowed due to rigid boundary conditions.

The basis of the model is a biased random walk

equation applied to the movement of each robot in

the system at each time step ∆t. For each robot

, k = 1..M, where M is the total number of ro-

bots, this equation takes the form:

= [(1 − ν

+ ν

(2)

where i = 0..N and the parameter ν

controls the

degree to which pure random choice (represented by

) dominates over weighted or biased choice repre-

sented by m

. There is also a step size s associated

with the random walk. Equation 2 and the stepsize to-

gether deﬁne the biased random walk. The vector m

represents weights based on locally visible values of

m(x, y, t) in the neighborhood of the walker. Given

only a single walker and m

purely based on trail lay-

ing (of marker) by the single walker, then a high value

of ν

leads to a random walk that approximates a self

avoiding walk.

Using 2 it is possible to experiment with local adap-

tive control strategies for selecting values of ν

and s

for each walker at each time step. This paper focuses

on the choice of ν

and experiments with adaptive val-

ues of s are left to future work. The approach taken

in this paper is to link increases in the value of ν

direction choices that are weighted by reinforced val-

ues of the m(x, y, t) ﬁeld. This creates a subset of

(greedy) candidate directions from the complete set of

possible direction choices. This subset may be empty

if no reinforced ﬁeld values are locally visible. These

direction choices are candidates for increased bias in

their probability of selection against random choice.

The aim of a local adaptive strategy for ν

is to fur-

ther reduce this subset of possible candidates (if this

can be done) by inhibiting the choice of some candi-

dates. In this paper the strategy is evaluated by cal-

culating a set of measures along a path up to distance

sense

(maximum sensor range) in each candidate di-

rection. Initially 3 measures have been chosen: (1) the

magnitude of reinforcement; (2) the distance dist that

can be traversed before any boundaries or ﬁeld objects

(such as another robot walker) are encountered; (3) a

path gradient estimate calculated along the path up to

dist. Using a simple perceptron type activation func-

tion a strategy is activated depending on the values

of the measures and a set of weights. Strategies that

are evaluated but not activated inhibit the choice of a

candidate direction.

More formally, we need to ﬁrst calculate a rein-

forcement vector l



− 1.0 if m

> 1.0

0 if m

< 1.0

Then for each l

a vector r

(j = 0..2) is calcu-

lated which contains the required measures. Given

the three chosen measures, we have r

= l

, r

the distance that can be traversed along the path be-

fore a boundary or object is encountered and r

the path gradient estimate.

We deﬁne a strategy π for selecting a local con-

trol variable z as π

. The local strategy for selecting

ν(x, y, t) is then deﬁned as:

: ν = ν

+ p(r

, θ) ∗ f(l

, ν

max

) (4)

where f is an monotonically increasing scaling func-

tion of l

with lower limit ν

and upper limit ν

max

equals a constant positive parameter σ in the range

[0, 1], ν

max

is 1.0, θ is a threshold value, and p is an

activation function deﬁned as:

p(r

, θ) =



1.0 if

i=0

> θ,

−1.0 if

i=0

< θ.

ICINCO 2005 - ROBOTICS AND AUTOMATION

338

where the w

are weight parameters. Equation 4 is

equivalent to conditionally increasing ν, after cer-

tain conditions are satisﬁed which result in the ac-

tivation function ﬁring, by a factor between ν

and

max

which depends on the magnitude of l

. This is

based on a simple perceptron like behaviour to choose

an approximate new scaled value of ν in the range

[ν

, ν

max

The choice of a gradient measure in caculating r

used as a rough estimate of whether movement along

a particular path will lead towards less frequently tra-

versed parts of the domain (based on the m(x, y, t)

ﬁeld). As part of calculating the gradient estimate, a

scalar discount factor ζ is introduced to discount val-

ues of m which are more than one cell away from

the walker and which may have uncertainty associ-

ated with them due to changes in a cell value that will

take place by the time the walker gets to that cell.

At each timestep ∆t the simulation moves each ro-

bot according to (Eq. 2) and updates m which is dis-

cretized on a i by j grid as follows:

i,j

(t + ∆t) = m

i,j

(t) + ξ

i,j

(t),

∀0 < i < nx, 0 < j < ny (6)

where ξ

i,j

(t) is based on the pheromone deposited

by robots during their movement (positive or nega-

tive) and the pheromone decay rate R

for the current

timestep. On each timestep the following heuristic is

applied:

1. Calculate m

from m(x, y, t)

2. Perform mappings (global to local, negative to pos-

itive)

3. ∀m

> 1.0, set l

= m

− 1.0 (else l

= 0) and

normalize m

, l

4. Calculate a set of r

(greedy candidate measures)

5. Apply local strategies π

6. Calculate and normalize d

where normalization for a vector v

is calculated as

norm

. Due to normalization the strength-

ening of the probability of making one choice leads

automatically to the weakening of the probability of

choosing the other available choices.

3.3.1 Model parameters

The key model parameters are M the total number of

robots, n

, n

representing the discrete grid dimen-

sions, σ representing a constant ratio of random ef-

fects versus bias effects on robot movement, σ which

represents a threshold used to control the effect of re-

inforcement in the model, R

which represents the

decay rate applied to the magnitude of ﬁeld values

m(x, y, t), nsteps represents the number of steps

taken in the simulation, and r

seed

representing the

seed value used for the random number generator.

(i = 0..1) are weight parameters which are in the

series of initial experiments described below are as-

signed values using the following rules: w

= 1.0/r

= r

sense

; if ((|r

| > 1)AND(r

> 0)) then

= −1.0 else w

= 1.0.

4 RESULTS

A series of initial tests have been performed us-

ing a Java implementation of the model where

Java.util.Random was used as the random number

generator for randomly chosen motion. These tests

have all been performed with the following ﬁxed

model parameters: nx = 70, ny = 70, r

seed

2392093, R

= 0.0, and with variable values for the

other parameters. The metric chosen here to evalu-

ate the model for domain coverage has been percent-

age coverage (of the bounded domain) versus time

(number of iterations). A standard sigmoid func-

tion has been used for the scaling function f with

exp(−(r

− σ))/2.

The ﬁrst set of tests used just one robot to search

a maze type domain. Initially tests were undertaken

with no use of strategies and different values of σ (i.e.

this is the ﬁxed value of ν = σ case). It was found that

as σ was increased in this case (with the random walk

becoming more like a self-avoiding walk) that the do-

main coverage also increased. At domain boundaries

a reﬂective boundary condition needs to be strongly

enforced and this is achieved using high negative

marker values and reinforcement (in direction choice)

to deﬁne the boundary. In Fig. 1 the use of local

strategies to adapt the value of ν was compared with

the ﬁxed value (No strategy) case for σ = 0.75. The

results appear to indicate that the use of adaptive local

strategy can increase performance (domain coverage

versus time) but more experiments need to be per-

formed to examine this in detail. The strategy para-

meter sets used were Strategy1 = (θ = 2.8, σ = 0.75)

and Strategy2 = (θ = 2.5, σ = 0.75) with other para-

meters set as described above.

The next set of simulation tests demonstrated that

the model scales well as the number of robots is in-

creased. Figure (3) shows that as the number of ro-

bots is increased from 1, to 8 the use of local strategy

adaption still provides beneﬁts over the no strategy

case but it is not as pronounced as in the single robot

test. The strategy parameter set (θ = 2.5, σ = 0.95)

is used for these simulation runs.

ADAPTIVE STRATEGY SELECTION FOR MULTI-ROBOT SEARCH BASED ON LOCAL COMMUNICATION

AND SENSING

339

Figure 2: Single robot search on maze domain with n

70, n

= 70, r

seed

= 2392093, R

= 0.0, and σ = 0.75.

”NoStrategy.dat” does not apply local strategy selection.

”Strategy1.dat” and ”Strategy2.dat” both apply strategy se-

lection. Starting position is (55, 35).

Figure 3: Multi robot search using 8 robots on

box canyon domain with n

= 70, n

= 70,

seed

= 2392093, R

= 0.0, and σ =

0.95. Starting positions are ((10, 60), (10, 10), (60, 60),

(60, 10), (15, 60), (15, 10), (50, 60), (50, 10)).

5 CONCLUSION

A simulation model is presented which can simulate

multiple robots using stigmergy as a decentralized co-

ordination mechanism for solving foraging and do-

main coverage type tasks. The model is derived from

a biased random walk using localized decisions as

the basis of walker movement. It is scalable to any

number of robots and able to represent complex do-

mains/environments. This model can be used to study

the effect of random versus biased decision mak-

ing (based on weighted estimates of path suitability)

through a set of local control parameters which allow

experimentation with locally adaptive strategy selec-

tion. A set of simple tests is used to demonstrate some

of the model features. The model introduced here will

allow the study of optimal local strategy for move-

ment to be studied in detail in a series of experiments.

These more detailed experiments will be the subject

of future work.

REFERENCES

Anderson, R. (1988). Random-walk learning: A neu-

robiological correlate to trial-and-error, In: Neural

Networks and Pattern Recognition. Academic Press,

Boston.

Azar, Y., Broder, A., Karlin, A., Linial, N., and Phillips, S.

(1992). Biased random walks. In 24th Annual ACM

Symposium on Theory of Computing, pages 1–9.

Balch, T. and Arkin, R. (1994). communication in reac-

tive multiagent robotic systems. Autonmous Robots,

1(1):27–52.

Baltes, J. and Anderson, J. (2003). Flexible binary space

partitioning for robotic rescue. In Proc. Int. Conf.

IEEE IROS 2003 - Intelligent Robots and Systems.

Coppersmith, D. and Diaconis, P. (1987). Random walks

with reinforcements. Stanford Univ. Preprint.

Davis, B. (1990). Reinforced random walk. Prob. Th. Rel.

Fields, 84:203–229.

Glover, F. and Kochenberger, G. A. (2003). Handbook of

Metaheuristics. Kluwer publishing.

Gonzales-Banos, H. and Latombe, J. (2002). Navigation

strategies for exploring indoor environments. Int. J.

Robot. Res., 21(10-11):829–848.

Holland, O. and Melhuish, C. (1999). Stigmergy, self-

organization, and sorting in collective robotics. Ar-

tiﬁcial Life, 5:173–202.

Igel, C., Friedrichs, F., and Wiegand, S. (2005). Evolu-

tionary optimization of neural systems: The use of

strategy adaptation. In Trends and Applications in

Constructive Approximation, Int. Series of Numerical

Mathematics. Birkhuser Verlag.

Kaelbling, L., Cassandra, A., and Littman, M. (1994). Act-

ing optimally in partially observable stochastic do-

mains. In Twelfth National Conference on Artiﬁcial

Intelligence.

Lam, L. and Pochy, R. (1993). Active-walker models:

growth and form in non-equilibrium systems. Com-

putation simulation, 7:534.

Montgomery, J. and Randall, M. (2002). Anti-pheromone

as a tool for better exploration of search space. In

Third International Workshop on Ant Algorithms,

ANTS 2002.

Patterson, D. J. and Kautz, H. (2001). Autowalksat:a self-

tuning implementation of walksat. Electronic Notes in

Discrete Mathematics (ENDM), 9.

Rekleitis, I., Dudek, G., and Milios, E. (2001). Multi-robot

collaboration for robust exploration. Annals of Math-

ematics and Artiﬁcial Intelligence, 31(1-4):7–40.

Stachniss, C. and Burgard, W. (2003). Mapping and explo-

ration with mobile robots using coverage maps. In

Proc. of the IEEE/RSJ International Conference on

Intelligent Robots and Systems (IROS).

Wagner, I. A., Lindenbaum, M., and Bruckstein, A. M.

(1999). Distributed covering by ant-robots using evap-

orating traces. IEEE transactions on robotics and au-

tomation, 15(5).

ICINCO 2005 - ROBOTICS AND AUTOMATION

340