MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME

HUMANOID MOTION GENERATION

Doik Kim, Youngjin Choi, and ChangHwan Kim

Intelligent Robotics Research Center

Korea Institute of Science and Technology (KIST)

39-1 Hawolgok-dong, Seongbuk-gu, Seoul 136-791, Korea

Keywords:

Humanoid, COG, COG Jacobian, Balancing, Motion Generation.

Abstract:

For a legged robot such as a humanoid, balancing its body during a given motion is natural but the most impor-

tant problem. Recently, a motion given to a humanoid is more and more complicated, and thus the balancing

problem becomes much more critical. This paper suggests a real-time motion generation algorithm that guar-

antees a humanoid to be balanced during implementing a given motion. A desired motion of each arm and/or

leg is planned by the conventional motion planning method without considering the balancing problem. In

order to balance a humanoid, all the given motions are embedded into the COG Jacobian. The COG Jaco-

bian is modiﬁed to include the desired motions and, as a result, dimension of the COG Jacobian is drastically

reduced. With the motion-embedded COG Jacobian, balancing and performing a task is completed simultane-

ously, without changing any other parameters related to the control or planning. Validity and efﬁciency of the

proposed motion-embedded COG Jacobian is simulated in the paper.

1 INTRODUCTION

A high mobility of a humanoid makes it difﬁcult to

generate a motion and to interact with environment in

real time. Many previous works in motion generation

of a humanoid is to replay a pre-deﬁned joint motion

and modify it little by a certain control method in real

situation. (Yamaguchi et al., 1999; Nagasaka et al.,

2004) For a complicated, smooth and agile motion, it

is necessary to develop a real time motion generating

method. In addition, it is desired to include dynam-

ics to improve the stability of a humanoid. Dynam-

ics, however, requires a large amount of computation.

The center of gravity(COG) can be a simple alterna-

tive of full dynamics, since it can be treated as a usual

kinematics which needs less computation than that of

dynamics, and ,furthermore, it reﬂects dynamic prop-

erties such as the mass and the mass center. Thus, the

COG is the important property which relates to the

stability, motion, and dynamics.

In order to use the COG relation in motion gen-

eration, the COG Jacobian is needed. The COG Ja-

cobian is ﬁrstly proposed by Kagami, et al, in 2000,

but they developed a numerical method(Kagami et al.,

2000). An analytic formulation of the COG Jaco-

bian is proposed by Sugihara, et al, in 2002(Sugihara

et al., 2002; Sugihara and Nakamura, 2002). They

used the COG Jacobian as follows: At ﬁrst, the ZMP

trajectory is predeﬁned and it is used as a desired mo-

tion of the COG Jacobian. Motions of some limbs are

used as constraints. An optimization problem that sat-

isﬁes the COG Jacobian and given constraints simul-

taneously, are solved to generate joint motion. As an

application, Sugihara, et al, used the COG Jacobian

for whole body cooperative balancing(Sugihara and

Nakamura, 2002), but the method needs large com-

putation in optimization.

The method proposed in this paper is that all the

given motions are embedded in the COG Jacobian to

generate joint motions in real time. In order to em-

bed motions into the COG Jacobian, a humanoid is

divided into several sections. A motion of each sec-

tion is considered independently, and relations of each

independent motion are combined with the motion-

embedded COG Jacobian. The dimension of the mod-

iﬁed COG Jacobian and the number of constraints are

reduced drastically, since motions are considered in-

dependently. In addition, the modiﬁed COG Jacobian

guarantees the balancing a humanoid and performing

a task.

This paper is organized as follows: Section 2 de-

scribes the overall system. Section 3 introduces

Kim D., Choi Y. and Kim C. (2005).

MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 55-61

DOI: 10.5220/0001187500550061

 SciTePress

the COG Jacobian suggested by Sugihara, et al, in

2002(Sugihara et al., 2002; Sugihara and Nakamura,

2002). Section 4 derives the motion-embedded COG

Jacobian. Section 5 simulates the suggested algo-

rithm, and section 6 concludes the paper.

2 OVERALL SYSTEM

For a human, if arms do a certain task, they focus on

the task not on the balancing. The remaining parts of

the human balance its body regardless of the task. The

proposed method, i.e., the motion-embedded COG Ja-

cobian, implements the fact. Consequently, when we

plan a motion, balancing problem does not need to be

considered, and furthermore, a conventional motion

planning method can be applied without any modiﬁ-

cation.

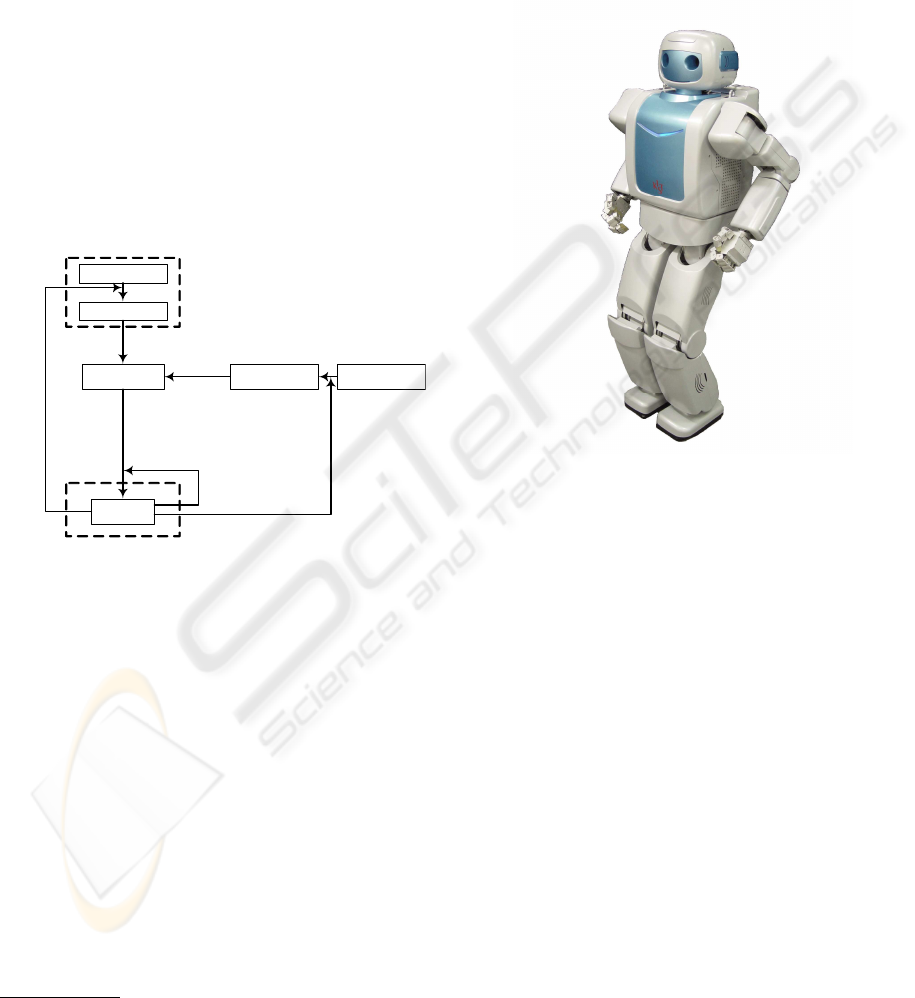
Desired COG-ZMP

Desired Arm & Leg

Motion

COG-ZMP Control

Motion Control

Inverted Pendulum Model

Motion Embedded

COG Jacobian

Joint Control

Humanoid

Angle

Real COG

& ZMP

Real Arm & Leg

Motion

Figure 1: Humanoid Control Flow

The overall control scheme can be divided into two

major categories: 1) COG and ZMP related algo-

rithms and 2) motion related algorithms. The COG-

ZMP related algorithms are based on the inverted

pendulum model

and the motion related algorithms

focus on how to distribute the COG-ZMP proﬁle

and given task motion to each joint with guaranteing

the balancing and performing the given task motion.

Fig. 1 shows the overall control ﬂow.

For the stability of a humanoid, the COG-ZMP pro-

ﬁle is predeﬁned for several basic motion, for ex-

ample, forward/backward movement, side movement

and turning. The COG-ZMP proﬁle is derived from

the inverted pendulum model, which gives relatively

simple relation. COG is calculated from the internal

In this paper, we don’t include the planning of COG

and/or ZMP. You can ﬁnd this subject in references(Hirai

et al., 1998; Choi et al., 2004).

joint information, thus it represents the pose of a hu-

manoid. ZMP is an dynamic property that represents

the stability whether a humanoid is to be rollover or

not. Two properties are tightly related, and therefore,

the predeﬁned COG-ZMP are controlled simultane-

ously with real COG and ZMP, in order to guarantee

the pose and the stability.

Figure 2: Mahru

Before developing the motion-embedded COG Ja-

cobian, a humanoid is divided into several parts. A

humanoid has four limbs attached at the main body.

Hereafter, each limb and the main body will be called

a section. For a human, a task is done with some sec-

tions, usually two arms, and balance the body with

other sections, usually two legs. It means that not

all sections are dedicated into one task, but they do

their own tasks, for example, balancing or a given

task. Thus the motion of each section can be given

independently. According to the existence of a given

desired motion, the section is classiﬁed into the idle

section and the busy section: the idle section has no

given motion and the busy section has a given mo-

tion. If a section has zero motion, i.e., it is ﬁxed at

current position, it can be considered as an idle sec-

tion or a busy section. In most case, a supporting sec-

tion which is attached on the ground are considered

as a busy section, since they have a role of balanc-

ing the body. A given motion of each limb or a main

body can be given as a joint motion and/or a Carte-

sian motion. If a busy section has a given motion in

the Cartesian space, it will be called C-busy section

ICINCO 2005 - ROBOTICS AND AUTOMATION

and a section with a given motion in the joint space

is J-busy section. Motion control step in Fig. 1 is

done for a C-busy section. A J-busy section will be

controlled at the joint control step.

The given motion and corresponding COG-ZMP

proﬁle are distributed to joints of a humanoid by us-

ing the COG Jacobian, i.e., the motion of the inverted

pendulum model is transformed into the motion of a

complicated multi-body model. By using the motion-

embedded COG Jacobian, the stability and a given

motion are guaranteed simultaneously.

The algorithm suggested in this paper is applied to

the humanoid, Mahru, developed at IRRC(Intelligent

Robotics Research Center), KIST in 2004 shown in

Fig. 2. Mahru has the height of about 150cm, and

the weight is about 67kg. It has 6-dof for each legs

and arms, 1-dof for the waist, 2-dof for the neck, and

each hand has 4-dof. In total, it has 35-dof. A stereo

camera is equipped.

3 COG JACOBIAN

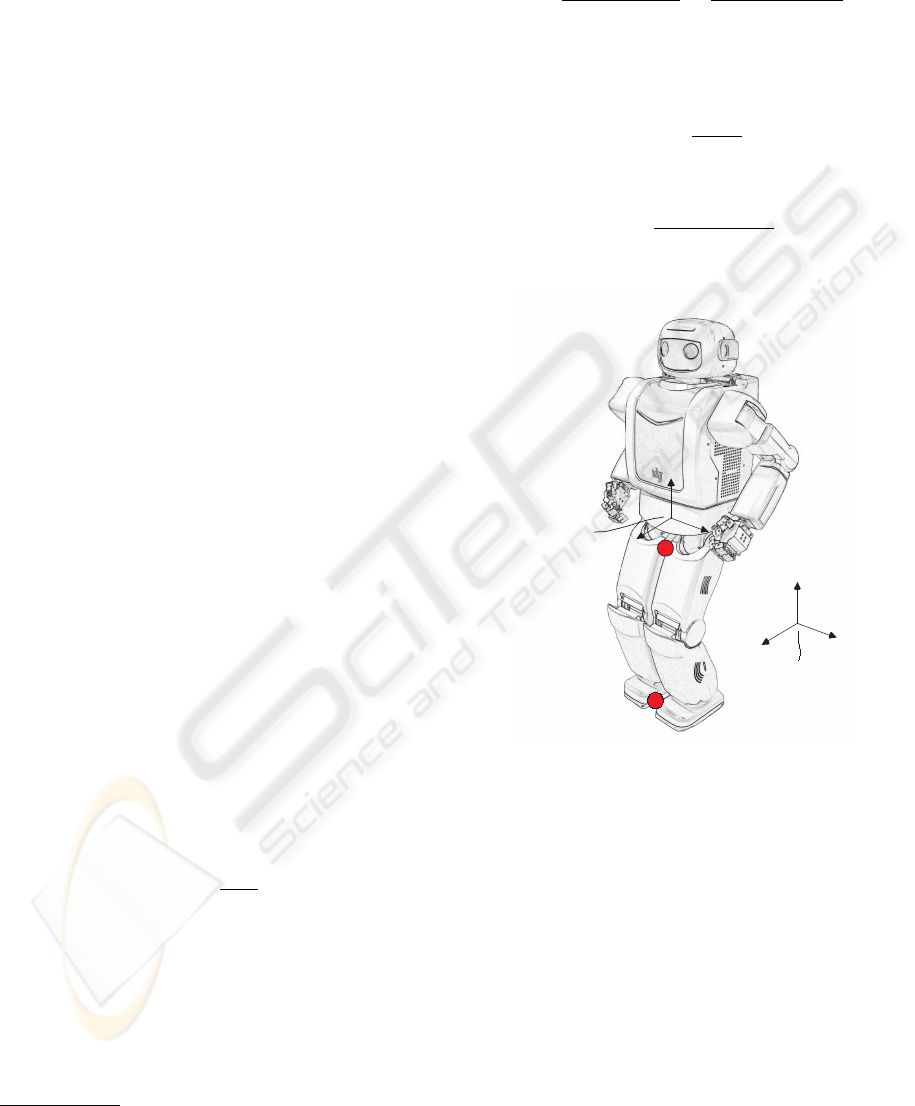
Let us consider a n-DOF humanoid. There are two

referential frames to describe a humanoid as shown in

Fig. 3. The world coordinate frame is ﬁxed on some-

where in the world and represents the global motion

of a humanoid. The body center frame is ﬁxed on a

humanoid to describe the local motion. Almost all

the properties of a humanoid is described in the body

center frame. The leading superscript

(·) implies that

the elements are represented in the body center frame,

and without it, a value is based on the world coordi-

nate frame.

The COG, p

, of a humanoid is a function of joint

angle vector, q, i.e., p

= f(q). Thus, there exists a

Jacobian J

which can relate

q to

as:

= J

q (1)

where the (3 × n) matrix J

is deﬁned by

≡

∂p

∂q

(2)

We call J

the COG Jacobian hereafter. p

is a quite

complex function with multiple arguments. Kagami,

et al, proposed the numerical method to calculate

it(Kagami et al., 2000), which unfortunately needs

a large amount of computation. Sugihara, et al, de-

veloped a fast and accurate calculation method of J

with the following approach(Sugihara et al., 2002).

This section is borrowed from Sugihara, et

al,(Sugihara et al., 2002; Sugihara and Nakamura,

2002).

Firstly, the relative COG velocity with respect to

the body center frame,

, can be expressed as:

n−1

i=0

n−1

i=0

n−1

i=0

n−1

i=0

(3)

where m

is the mass of link i,

is the position of

the center of mass of link i with respect to the body

center frame, and

(3 × n) is deﬁned by

≡

∂

∂q

(4)

Therefore, Jacobian

which relates

q to

n−1

i=0

n−1

i=0

(5)

Body Center

Frame

COG

X

Y

Z

World Coorinate

Frame

ZMP

Figure 3: Coordinate System of Mahru

Secondly, suppose link 1 is the base section, which

is ﬁxed in the world frame (for example, when the

right leg is the supporting leg, the right leg is ﬁxed on

the ground and becomes the base section), the COG

velocity with respect to the world coordinates frame,

+ ω

× R

+ R

{

−

+ (

−

) ×

}

+ R

{−

+ [(

−

)×]

}

(6)

where p

is the position of the body center, ω

is the

angular velocity of the body center, and R

is the at-

titude matrix of the body center with respect to the

MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION

world frame.

is the position of the base section,

is the angular velocity of the base section,

the linear velocity part of the base Jacobian and

is the angular velocity part of the base Jacobian with

respect to the body center frame. [v×] means outer-

product matrix of a vector v (3 × 1).

is the joint

velocity of section i. Note that the base section can be

any section that is ﬁxed on the ground, but here, we

assigned the base section with the number 1 without

loss of generality.

In order to use Eq. (6) in the following section, it is

rewritten here as:

i=1

+ R

{−

+ [(

−

)×]

}

(7)

where m is the number of sections.

Now, let us derive the motion-embedded COG Ja-

cobian from Eq. (7).

4 MOTION-EMBEDDED COG

JACOBIAN

4.1 Embedment of J-Busy Section

It is easy to embed a joint motion into the COG Jaco-

bian, since the joint motion can be directly replaced

in Eq. (7).

If section j is a J-busy section, Eq. (7) becomes

− R

i=1,i6=j

+ R

{−

+ [(

−

)×]

}

(8)

The second term of the left hand side compensates

the motion of the jth section. Therefore, the other

sections shown in the right hand side can generate a

joint motion with the compensated COG motion.

If at least one section, i.e., the base section, is an

idle section, then Eq. (8) can compensate motions of

the other sections. If all sections are the J-busy sec-

tion, there is no section to compensate given motions.

In this case, an optimization method needs to be ap-

plied.

4.2 Embedment of C-Busy Section

Let us derive the motion-embedded COG Jacobian for

the C-busy section. Each section of a humanoid is

considered as an independent section, i.e., any section

can have its own motion independently without con-

sidering other sections. In general, the i-th section has

the following relation:

(9)

where

= [

;

]

is the end point velocity of

the section,

and

are the linear and the angular

velocity, respectively.

is the joint velocity, and

is the usual Jacobian matrix represented in the body

center frame.

In our case, the body center is ﬂoating, and thus the

end point motion about the world coordinate frame is

written as follows:

= X

−1

+ X

(10)

where

= [

; ω

]

is the velocity of the body

center represented in the world coordinate system,

and



×]



(11)

is a (6 × 6) matrix which relates the body center ve-

locity and the end point velocity of the i-th section.

and 0

are the (3 × 3) identity and zero matrix,

respectively. R

is the orientation of the body center

based on the world coordinate system.

is the posi-

tion vector from the body center to the end of the i-th

section based on the body center frame. The transfor-

mation matrix X





. (12)

By combining Eq. (9) and Eq. (10), the end point

velocity based on the world coordinate system is

= X

−1

+ X

(13)

For simplicity, we will use the relation J

, hereafter.

From Eq. (13), we can see that all sections should

satisfy the compatibility condition, i.e., the body cen-

ter velocity,

, in Eq. (13) for each section is the

same, so that sections are connected without being

broken., and thus arbitrary two sections, for example,

the i-th and j-th section should satisfy the following

relation:

(

− J

) = X

(

− J

). (14)

From Eq. (14), the joint velocity of any section can

be represented by the joint velocity of any other sec-

tion. However, all sections will be represented by the

base section, since the motion of the body center is

represented by the base section, as shown in Eq. (7).

The base section can be the supporting leg in the sin-

gle supporting phase or one of both legs in the double

supporting phase if a humanoid is standing. Let us

ICINCO 2005 - ROBOTICS AND AUTOMATION

express the base section with the subscript 1, then the

joint velocity of any section is expressed as:

= J

−1

− J

−1

(

− J

), (15)

for i = 2, · · · , m, where m is the number of sections.

Here,



(

−

)×]



. (16)

Note that if a section is a redundant system, any null

space optimization scheme can be added in Eq. (15),

and J

−1

becomes a generalized inverse.

By substituting Eq. (15) into Eq. (7), the motion-

embedded COG Jacobian relation becomes

= R

{−

+ [(

−

)×]

}

i=1

−1

(

− X

)

i=1

−1

(17)

where J

= R

and J

= R

are the

linear and angular velocity part of the base section

Jacobian. Note that if i = 1,

− X

= 0 and

−1

= R

Finally, all desired motions,

, are embedded in

the modiﬁed COG Jacobian. Thus the effect of the

COG movement generated by the desired motion is

compensated by the base section. Eq. (17) can be

rewritten like the usual kinematic Jacobian of the base

section:

meG

= J

meG

(18)

where

meG

−

i=1

−1

(

− X

), (19)

meG

= R

{−

+ [(

−

)×]

}

i=1

−1

. (20)

The modiﬁed COG motion,

meG

, consists of two

relations: a desired COG motion(the ﬁrst term) and

the relative effect of motions of each section(the sec-

ond term). The modiﬁed COG Jacobian, J

meG

also

consists of two relations: the effect of the body cen-

ter(the ﬁrst term) and the effect of motions of each

section(the second term).

The modiﬁed COG Jacobian J

meG

is a (3 × n

)

matrix where n

is the dimension of the base sec-

tion, which is smaller than that of the original COG

Jacobian. For example, Mahru in Fig. 2 has a 6-dof

leg, and thus n

= 6 if the leg is the base section.

After solving Eq. (18), the joint motion of the base

section is obtained. The resulting base section mo-

tion balances a humanoid robot automatically during

the movement of all other sections. With the resulting

joint motion of the base section, the joint motion of all

other sections are obtained by Eq. (15). The resulting

motion follows the desired motion, regardless of the

balancing motion of the base section.

5 SIMULATION

In order to show the validity of the suggested algo-

rithm, a dynamic simulator developed at IRRC, KIST

is used. The simulator can simulate a humanoid

Mahru shown in Fig. 2.

To show the effect of the J-busy and C-busy sec-

tion, simultaneously, two arms are J-busy and two

legs are C-busy. The left and right foot is moved

up and down, in turn, with a sinusoidal function.

Two motions for arms are given: 1) both arms are

stretched forward as shown in Fig. 4 and 2) the right

arm is raised and waves it shown in Fig. 5. The de-

sired arm motions are obtained by the motion cap-

tured data(Kim et al., 2005). In order to move the

COG to the center of the supporting foot, a predeﬁned

COG-ZMP trajectory is applied.

The ﬁrst motion, stretching two arms forward, can

make the humanoid fall down since the mass center is

moved in front of the humanoid. By using the motion-

embedded COG Jacobian, the desired motion of arms

are compensated by the supporting leg, and thus the

leg moves the humanoid body back automatically as

shown in Fig. 4 (b), the side view.

The second motion, rasing and waving right hand,

makes a large disturbance to the humanoid since the

fast waving motion changes the mass center quickly

to the left and right. Thus if the right hand goes to the

right side when the right foot is off the ground, it is

difﬁcult to move the COG and ZMP to the stable re-

gion, i.e., the left foot. However, the left leg compen-

sates the motions of arms by the motion-embedded

COG Jacobian, and consequently, the COG and ZMP

are still in the stable region as shown in Fig. 5.

The overall motions are complicated and it is easy

to make the humanoid unstable. However, by using

the motion-embedded COG Jacobian, any parameters

such as control gain, COG/ZMP trajectory, and etc,

do not need to be changed to stabilize or balance the

humanoid.

6 CONCLUDING REMARK

In this paper, a real-time motion generation method

for a humanoid is suggested. A desired motion of

each section is obtained by the conventional motion

MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION

planning method without considering the balancing

problem.

The method can balance a humanoid by using the

motion-embedded COG Jacobian, which reduces the

computation time to generate a motion and satisﬁes

the given motion and the balance, simultaneously.

Validity and efﬁciency of the suggested method is

examined by the simulation. Two motions are ap-

plied to the humanoid, and without changing any pa-

rameters on the control or planning, the humanoid ac-

complishes the given motions and it also balanced its

body.

In the paper, we assume that all the sections have

their own tasks. If a section does not have a desired

motion, i.e., an idle section, there are two possible

cases:

1. the idle section is considered as a busy section with

a zero motion, i.e., it is ﬁxed at the current position.

In this case, the section is considered as a C-busy

section, and the method suggested in this paper can

be applied.

2. with some optimization scheme, the idle section is

used actively to balance the humanoid. Since the

idle section has no desired motion, by changing

its position actively, the humanoid can balance the

body more easily and naturally. The optimization

of the idle section is still under development.

REFERENCES

Choi, Y., You, B.-J., and Oh, S.-R. (2004). On the stability

of indirect ZMP controller for biped robot systems.

In International Conference on Intelligent Robots and

Systems, pages 1966–1971.

Hirai, K., Hirose, M., Haikawa, Y., and Takenaka, T. (1998).

The development of honda humanoid robot. In IEEE

International Conference on Robotics and Automa-

tion, pages 1321–1326, Leuven, Belgium.

Kagami, S., Kanehiro, F., Tamiya, Y., Inaba, M., and Inoue,

H. (2000). Autobalancer: An online dynamic balance

compensation scheme for humanoid robots. In The

4th International Workshop on Algorithmic Founda-

tion on Robotics (WAFR’00).

Kim, C.H., Kim, D., and Oh, Y. (2005). Solving an

inverse kinematics problem for a humanoid robot’s

imitation of human motions using optimization. In

ICINCO2005, (accepted).

Nagasaka, K., Kuroki, Y., Suzuki, S., Itoh, Y., and Yam-

aguchi, J. (2004). Integrated motion control for walk-

ing, jumping and running on a small bipedal enter-

tainment robot. In IEEE International Conference on

Robotics and Automation, pages 3189 – 3194.

Sugihara, T. and Nakamura, Y. (2002). Whole-body co-

operative balancing of humanoid robot using COG ja-

cobian. In International Conference on Intelligent Ro-

bots and Systems, pages 2575–2580, EPFL, Lausanne,

Swizerland.

Sugihara, T., Nakamura, Y., and Inoue, H. (2002). Realtime

humanoid motion generation through ZMP manipula-

tion based on inverted pendulum control. In IEEE In-

ternational Conference on Robotics and Automation,

pages 1404–1409, Washington, DC.

Yamaguchi, J., Soga, E., Inoue, S., and Takanishi, A.

(1999). Development of a bipedal humanoid robot —

control method of whole body cooperative dynamic

biped walking. In IEEE International Conference on

Robotics and Automation, pages 368–374.

ICINCO 2005 - ROBOTICS AND AUTOMATION

(a) front view

(b) side view

Figure 4: example 1: both arms move forward

(a) front view

(b) side view

Figure 5: example 2: right arm is raised and waves

MOTION-EMBEDDED COG JACOBIAN FOR A REAL-TIME HUMANOID MOTION GENERATION