
PRODUCTION TIME MINIMIZATION STRATEGIES IN A
FLEXIBLE MANUFACTURING ENVIRONMENT
A Tabu Search approach
Antonio Gabriel Rodrigues, Arthur Tórgo Gómez, José Vicente Canto do Santos
Masters in Computer Applied, Unisinos University, Av. Unisinos 950, São Leopoldo,Rio Grande do Sul, Brazil
Keywords: Tabu Search, Scheduling Problem, Flexible Manufacturing Systems.
Abstract: In this paper is proposed a computational model (“Modelo de Seleção de Partes e Escalonamento” – MSPE)
to generate a scheduling of parts in a Flexible Manufacturing System environment, considering due dates,
production turns and machine tools with magazine constraints. The problems considered are the Part
Selection Problem and the Scheduling Problem. The scheduling objectives are the minimization of
switching tools time, stop instants total time and the parts tardiness. The optimization police are defined
according to Objective Function’s weights values.
1 INTRODUCTION
In this paper are presented analysis of politics of
production optimization through the management of
the weights of an objective function. To make this
analysis, a computational model was constructed
considering the Part Selection Problem and the
Scheduling Problem in a job shop of a Flexible
Manufacturing System. The due dates and the
magazine machine constraints are taken in account.
The techniques chosen, for the construction of the
model, are the Cluster Analysis and the Tabu
Search.
2 PROBLEMS STUDIED AND
TECHIQUES CHOSEN
The focus of this study is a Flexible Manufacturing
System, where two classic problems are treated: the
Part Selection Problem and the Scheduling Problem.
As can be seen in bibliography (Groover, 2001;
Dorf, 1994; Crama, 1997), a FMS can be composed
of three basic components: (i) a set of CNC/DNC
machines (Computer Numerical Control /
Distributed Numerical Control) which possess a
device for tool storage (magazine) with restricted
capacity and a automatic system of tool exchange;
(ii) an Automated Material Handling System
(AMHS) that links the machines with the part
storage an the warehouse, carrying parts and tools to
the production line; (iii) a computational system that
manages both the machine and the AMHS systems.
Considering general-purpose machines, the entire
system can be treated as one machine (Hwang,
1987). In this paper, the FMS considered is
composed of one CNC/DNC machine, a AMHS and
a computational control system.
In this environment, the first problem studied is the
Part Selection Problem, which consists in group
parts that possesses similar attributes in Part
Families (PFs) (Groover, 2001; Kusiak, 1992) to
take advantage of their similarities in design and
production. In this study, the attribute chosen to
generate PFs is the type of tool needed to process a
set of parts. The parts of a same PF can be
processed by the machine without stop for tool
switching (setup). The complexity of this problem is
NP-Complete (Hwang, 1987).
The second studied problem is the Scheduling
Problem, where the classic goal is generate a
schedule of parts which respects due dates
constraints. Other constraints can be considered,
such as magazine constraints, machine waste time
constraints and production turns. The Scheduling
Problem is difficult to solve and possesses
computational complexity NP-Hard (Crama, 1996).
Various authors use heuristic methods to deal with
complexity
(Kusiak, 1992).
To solve the Scheduling Problem, a Tabu Search
approach was proposed (Glover, 1997). This
technique has been applied in combinatorial
467
Gabriel Rodrigues A., Tórgo Gómez A. and Vicente Canto do Santos J. (2005).
PRODUCTION TIME MINIMIZATION STRATEGIES IN A FLEXIBLE MANUFACTURING ENVIRONMENT - A Tabu Search approach.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 467-470
DOI: 10.5220/0001187704670470
Copyright
c
SciTePress

optimisation problems, such as Travel Salesman
Problem, Time Tabling Problem, Job Shop
Scheduling Problem (Widmer, 1991).
3 PROPOSED MODEL
The MSPE model deals to generate a schedule that
minimizes the following production times:
tardiness time: sum of differences between the
predefined due date and the part completion date;
switching tools time: is the time to retrieve and
insert tools in the magazine. The time to switching
tools is proportional to the number of tools
exchanged, here the time to exchange one tool is
considered as one constant;
setup time: time to clean the workspace,
maintenance of the machine, handling off the
processed parts and restart the machine to the new
operations.
The managing of the significance of these times it’s
made through the definition of values for the
Objective Function’s weights. The objective
function was developed considering two
dimensions: physical dimension (Part Families
generation) and time dimension ( scheduling).
Considering:
s a feasible solution;
N = total amount of parts;
L = number of setups in s;
U = number of switching tools in s;
i = index of a part;
j = index of a setup;
k = index of a switching tool;
Dvi = due date of part i;
Dsi = completion date of part i ;
Tr = time to restart the machine;
Te = time to exchange one tool.
Minimize:
),(),(),(),(),(
321
tpStPtpSptpPtpAtPtpf
∗
+∗+∗=
Where
∑
=
−=
N
i
ii
DsDvtpAt
1
)(),( such (Dv
i
–Ds
i
) ≥ 0,
},...,1{ Ni ∈
;
TrSptpSp
L
j
j
∗=
∑
=1
),( such Sp
j
≥ 0, Tr
≥ 0,
},...1{ Lj ∈ ;
TeSttpSt
U
k
k
∗=
∑
=1
),(
such St
k
≥ 0, Te ≥ 0,
},...,1{ Uk ∈ ;
and
P
1
≥ 0, P
2
≥ 0 e P
3
≥ 0.
4 EXPERIMENTS
The model’s implementation was made in C++
language, using GCC compiler in a GNU-Linux
operational system. A Pentium III 833Mhz 128MB
RAM was used to perform the experiments batches.
The experiments were made according three
optimization politics: (i) minimization of switching
tools time, (ii) minimization of setup time, and (iii)
minimization of tardiness time. In all experiments t
were considered: a set of 10 parts and 9 tools to
process them; the maximum capacity of the
magazine is 4 tools; the time spend for each tool
switch is 4 minutes; the time for restart the machine
operation is defined as 5 minutes; the production
period (turn) is defined as 480 minutes; the tabu list
stores 5 forbidden moves; and nbmax number is
defined as 100 iterations. It was made 100
experiments with the MSPE to define the initial
value of the Objective Function f weights. In these
experiments the values of the each weight are
randomly varied in a 0 - 100 uniform distribution
interval. The behavior of the results generated was
observed and any optimization policies were used.
It was noticed that the results generated favors the
minimization of tardiness. This is due to the fact
that the weight of the tardiness (At) are significantly
high compared to the 2 others weights (St and Sp).
The results obtained in these experiments are the
following:
Table 1: Initial solution obtained in the experiments to
define the initial values of weights of f
Average
makespan 499,69 min 4,83 min
At 425,68 min 109,85 min
Sp 24,65 min 1,28 min
St 43,04 min 3,56 min
The best result was encountered in a average of 3,47
iterations (σ 3,39). In a manner to obtain a solution
in which any decision variable of f were privileged
(non-tendentious solution), the average of the
weights of St an Sp (P
2
and P
3
) were divide by the
average of the weight of At (P
1
). The proportion
reached is:
P
1
= P
2
* 17,27 and P
1
= P
3
* 9.89
Once defined a proportion among the weights of f
that constitutes a non-partial solution, the MSPE
Module 4 is run with the weights P
1
= 1, P
2
= 17,27
and P
3
= 9,89. The result is showed in Table 2.
ICINCO 2005 - ROBOTICS AND AUTOMATION
468
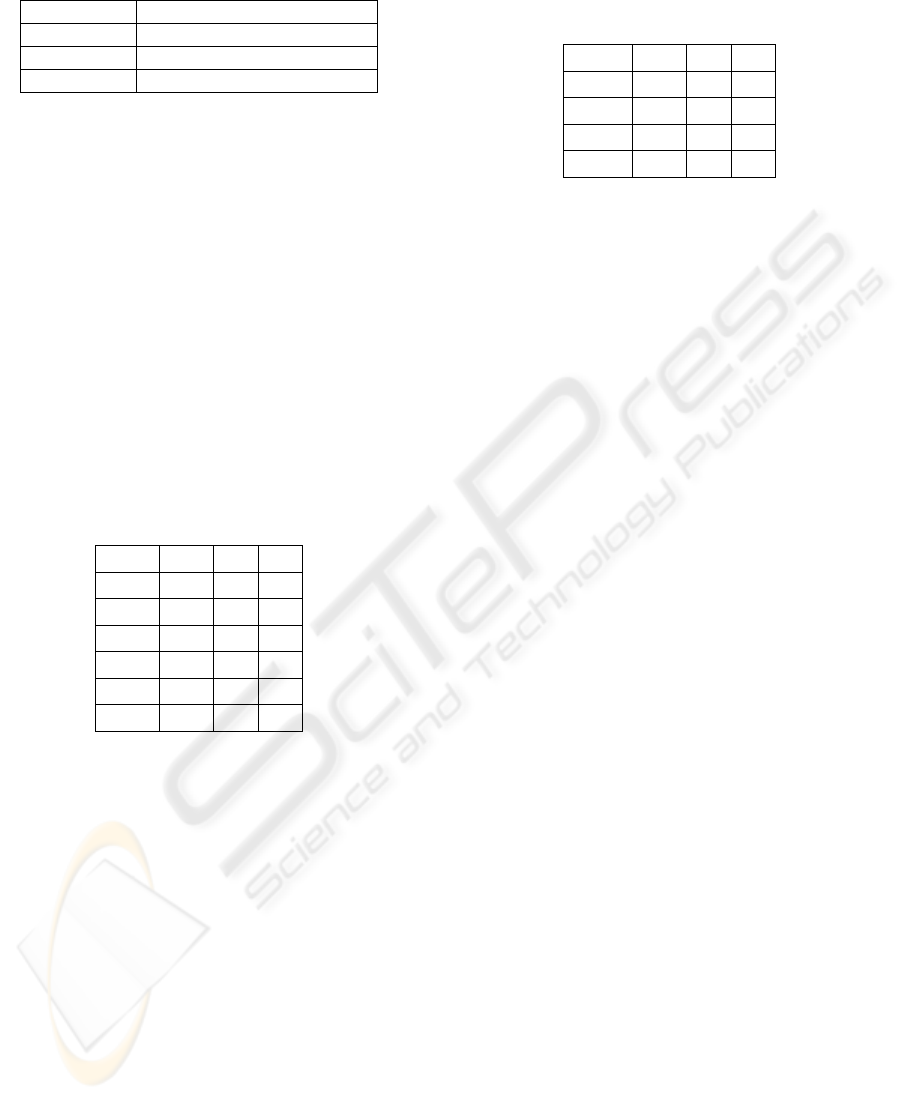
Table 2: solution obtained with non-tendentious
solution’s weights
makespan 501 min.
At 397 min.
Sp 25min. (5 setups)
St 44 min. (11 tool switches)
In the experiments described in the following items,
the different optimization policies are analyzed
through the managing of the values of the weights
of Objective Function f. For these experiments the
values obtained in the non-tendentious solution are
used as initial point.
4.1 Switching tools time minimization
The objective of this experiment is minimize the
time of switching tools (St) favoring P
3
weight. The
weights P
1
and P
2
were made constants with the
values of the non-tendentious solution. The weight
P3 was varied, starting with non-tendentious
solution (9.89) and increased of 5 units until reach
value close to 1000. The table below summarizes
the experiment results.
Table 3: Switching tools time minimization
P
3
At Sp St
9,89 397 25 44
20 624 20 36
40 709 20 32
45 709 20 32
50 891 20 28
1000 891 20 28
The increment of P
3
makes the variable St more
significant and the others (At ad St) have them
influence reduced. The increasing of the At value
denotes a existent conflict between minimize
tardiness time and minimize tool switch time. It was
made experiments were At was not considered (P
1
=
0) and P
2
fixed in 17,27. In these experiments, for
values of P3 higher than 9,89 the tool switches time
and the setup time is lower (28 and 20 minutes,
respectively), and At increases to 1029 minutes.
4.2 Setup time minimization
The objective in this experiment is minimize the
setup time (Sp). It is considering that the value of Sp
weight P
2
is increased and the values of P
1
and P
3
are constants, having the value of the non-
tendentious solution. The initial value of P
2
was
17,27, being increasing of 5 units per run.
The results of the 20 experiments that were made
are summarized in the table below.
Table 4: Setup time minimization
P
2
At Sp St
17,27 397 25 44
20 397 25 44
500 624 20 36
1000 624 20 36
In the initial solution, the parts were grouped in 5
PFs, so the minimum number of batches is the same
number of PFs. Between the processing of these
batches its necessary tool switching (4 setups in this
situation). In this case, considering the Objective
Function, the setup time would be equal to 20
minutes. In the experiments performed, with P
2
› 25,
the schedules generated by MSPE had the minimum
setup time.
Although the setup time resulting of the increment
of P
2
had be the same that the setup time
encountered in the P
3
experiments, the switching
tools time reached with P
2
is higher. It was
identified in P
3
experiments the existence of a
relation between the minimization of St and Sp. So,
the minimization of St implies in a minimization of
Sp, but in the other hand, the minimization of Sp
does not lead St to its minimum value.
4.3 Tardiness time minimization
In this experiment the behavior of the solutions
generated by MSPE are analyzed, considering the
initial solution presented in the table 1, where
tardiness time is privileged. Once the initial solution
privileges the tardiness time reduction (962 to 397
minutes in the initial solution), the increasing of P
1
doesn't influence the behavior of the results in this
experiment (At=397, Sp = 25 and St=44).
4.4 Tabu list and nbmax variation
The size of the tabu list and the tabu search
parameter nbmax were varied in these experiments,
in order to verify the influence of these in the results
of f. Four categories of experiments were made:
using values of weights of the non-tendentious
solution (P
1
=1, P
2
=17.27 and P
3
=9.89);
using weights that privilege St (P
1
=1, P
2
=17.27 and
P
3
=100);
using weights that privilege Sp (P
1
=1, P
2
=100 and
P
3
=9.89); and
using weights that privilege At (P
1
=100, P
2
=17.27
and P
3
=9.89);
PRODUCTION TIME MINIMIZATION STRATEGIES IN A FLEXIBLE MANUFACTURING ENVIRONMENT - A
Tabu Search approach
469

The tabu list size was increased in 50 units while
nbmax was increased in 100 units per run. The
results obtained are summarized in the next tables.
Table 5: Tabu list size and nbmax variation for weights of
the non-tendentious solution
nbmax tabulist At Sp St
200 100 397 25 44
… … … … …
1000 500 397 25 44
Table 6: Tabu list size and nbmax variation for solution
that privileges St
nbmax tabulist At Sp St
200 100 891 20 28
… … … … …
1000 500 891 20 28
Table 7: Tabu list size and nbmax variation for solution
that privileges Sp
nbmax tabulist At Sp St
200 100 624 20 36
… … … … …
1000 500 624 20 36
Table 8: Tabu list size and nbmax variation for solution
that privileges At
nbmax tabulist At Sp St
200 100 355 30 56
300 150 397 25 44
400 200 355 30 56
500 250 397 25 44
600 300 355 30 56
700 350 344 30 56
800 400 361 30 56
900 450 397 25 44
1000 500 397 25 44
5 CONCLUSIONS
In this paper was proposed a computational model,
the MSPE, that considers Part Selection Problem
and Scheduling Problem in a job shop. This model
allows that starting with a set of parts and tools
could be obtained a scheduling that reflects
optimization strategies through the managing of the
weights of an objective function. Experiments were
performed, in which, the values of the weights of
the objective function were varied according to 3
strategies of minimization: (i) tool switches time,
(ii) setup time and (iii) tardiness time. To perform
the analysis it was defined an initial solution for the
Objective Function weights, with the intent of all
variables had the same contribution for the result of
f. Considering the high significance of the tardiness
time variable, the initial solution privileged this
variable. In the minimization of the switching tools
time it was identified a conflict between this
objective and the tardiness time minimization. As in
the St experiments, the Sp minimization conflicts
with At minimization. The increasing of weight
value of Sp reduces the influence of At, but do not
lead St to its minimum value. This is due to the fact
that for the same setup time exists two or more
different tool switches times. The minimization of
the tardiness time can be verified with the
increasing of the tabu list size and the nbmax. As in
the other experiments, the times of setup and
switching tools became higher as At is increased. In
this experiments, the increasing of tabu list size and
nbmax has positive impact in the tardiness time
minimization. A tabu list with higher size acts as
diversification factor, forcing the tabu search to visit
a higher number of feasible solutions in the
neighborhoods generated.
REFERENCES
Crama, Y., Combinatorial Optimization models for
production scheduling in automated manufacturing
systems, European Journal of Operations Research,
Elsevier, p. 136 – 156, 1997.
Dorf, R., Kusiak, A., 1994. Handbook of Design,
Manufacturing and Automation, John Wiley and Sons.
Glover, F., Laguna, M., 1997. Tabu Search, Kluwer
Academic, Boston.
Groover, M. P. Automation, Production Systems, and
Computer-Integrated Manufacturing, United States:
Prentice Hall, 2001, Segunda Edição, 856p.
Hwang, S. S., SHOGAN, A. W. Modeling and Solution of
an FMS Part Selection Problem, University of
Califormia, California, 1987.
Kusiak, A., 1992. Intelligent Design and Manufacturing,
John Wiley and Sons.
Widmer, M., 1991. Job Shop Scheduling with Tooling
Constraints: a Tabu Search Approach. Journal of
Manufacturing.
ICINCO 2005 - ROBOTICS AND AUTOMATION
470
