A STUDY OF CLASSIFICATION TECHNIQUES APPLIED TO

CBERS SATELLITE IMAGES

Priscila Andrea da Rocha Severino,

Rossana Baptista Queiroz,

Arthur T

orgo G

omez,

Luiz Paulo Luna de Oliveira

Masters in Computer Applied, Unisinos University

Avenida Unisinos , 950, S

ao Leopoldo, Rio Grande do Sul, Brazil

Keywords:

Neural Networks, Fractal Dimension, Image Classiﬁcation, Error Minimization.

Abstract:

In this paper its presented classiﬁcation methods for identify forests with araucaria angustifolia, using artiﬁcial

intelligence and Fractal approach. Studies were made to perform experiments in which could be veriﬁed the

suitable of ANNs for classiﬁcation of CBERS satellite images. However, it was noticed in that classiﬁcation a

signiﬁcant error exists. Then, it intends to continuity that study through the incorporation of new techniques of

treatment of the images before the submission to Neural Networks training with the use of error minimization

techniques. When applying the detection of borders in those images, it was noticed that those limits possesses,

visibly, patterns that could be good as additional information for identiﬁcation of a class. Therefore, it is

supposed that those differences can be quantiﬁed by Fractal Dimension calculation, whose deﬁnition is going

of encounter with the need of establishing patterns for those borders or limits. Fractal Dimension study

veriﬁes the adaptation of that technique to determine areas that the Neural Networks and the method Maximum

Likelihood doesn’t get to distinguish.

1 INTRODUCTION

The satellite image information can be extracted

through classiﬁcation of these images. There are vari-

ous classiﬁcation methods that try through several ap-

proaches to identify with accuracy the information of

each image pixel, classifying them in categories or

classes according to their spectral information. Im-

age classiﬁcation methods can have different accu-

racy levels, according their approach and parameters

speciﬁcation. Some of pixel classiﬁcation methods

that are more used by Geographic Information System

(GIS) are based in statistical inference. In this context

it’s checked if the Artiﬁcial Intelligence based tech-

nique is suitable for image classiﬁcation (W. Gonza-

lez, 2000) (Haykin, 1999) (Feder, 2000). In this paper

it’s presented in its ﬁrst section a comparative study

between two satellite image classiﬁcation techniques:

the Statistical Method of Maximum Likelihood (ML)

and an Artiﬁcial Intelligence technique, based on the

learning of Artiﬁcial Neural Networks (ANNs).Due

to confusion that both methods obtained in some re-

gions, it is proposed in this article the development of

an approach that involves information of image areas

(sets of pixels) instead of pixel-to-pixel information.

In this paper it is showed that he Fractal Dimension

concept can be applied to supply the need of to ac-

complish the identiﬁcation of the classes in that the

studied methods didn’t get to identify with accuracy.

In section 3, its presented the initial experiments made

in CBERS 2 images, where fractal dimension will be

used to distinguish two interest class.

2 MAXIMUM LIKELIHOOD vs.

ARTIFICIAL NEURAL

NETWORKS

In order to classify an image of the CBERS-1 satel-

lite were used the Maximum Likelihood method and a

method based in the training of Artiﬁcial Neural Net-

works, whose detailed description can be seen in other

works.

In the experiments accomplished with those classi-

ﬁers, it was observed a high rate of success of both

methods for the classes water and forest (the classes

identiﬁed were: water, forest, no-forest and Defor-

estation).The Kappa coefﬁcient calculated (0,65 for

MAXVER and 0,64 for the RNAS) is considered sub-

471

Andrea da Rocha Severino P., Baptista Queiroz R., Tórgo Gómez A. and Paulo Luna de Oliveira L. (2005).

A STUDY OF CLASSIFICATION TECHNIQUES APPLIED TO CBERS SATELLITE IMAGES.

In Proceedings of the Second Inter national Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 471-474

DOI: 10.5220/0001187804710474

 SciTePress

stantial for both methods. The classiﬁer based in

Neural Networks presented satisfactory results, com-

pared with the Maximum Likelihood. This indicates

that this method demonstrated that it is suitable for

the classiﬁcation of satellite images. However it is

observed that both methods tend to confuse the ar-

eas of the deforestation class with the no-forest class.

It is believed that that confusion happen because the

grayscale values of the p

ıxeis of those two classes are

very close. For that reason it was started the study of

Fractals as a Minimization Error Technique.

2.1 Study of the Minimization Error

Technique

Through the study and of the accomplished experi-

ments it was veriﬁed that the classiﬁcation neural is

suitable for the images of the satellite CBERS. How-

ever, this classiﬁcation still has a signiﬁcant error. It

is intended to give continuity to this study through

the incorporation of new techniques of treatment of

the images before the submission to Neural Networks

training and of techniques for Minimization of Error.

One of these techniques intend to decrease the error

of the classiﬁcation that happens in the borders, or

transition limits between a class and another. It is ob-

served in the images that some classes present very

deﬁned limits and with different characteristics. If it

is applied border detection in these images is noticed

that those limits have visibly patterns or irregularities

that could be used as additional information for iden-

tiﬁcation of a class. It is supposed that those differ-

ences can be quantiﬁed by Fractal Dimension calcu-

lus (Feder, 2000), whose deﬁnition supplies the need

of establishing patterns for those borders or limits.

Fractal Dimension study veriﬁes the adaptation of

that technique to determine areas that the ANNs and

the method ML doesn’t get to distinguish.

2.2 Fractal Dimension

Fractal objects are not measured by length or area.

They are “more” than lines and “less” than a plane.

To measure them, it is used the concept of Fractal Di-

mension. Fractal Dimension is a measure that quanti-

ﬁes the fractal density in the metric space it is deﬁned,

being used for compare it. (Feder, 2000) (Conci,

2004) .

2.3 Fractal Dimension Calculus

In geometric objects (with dimension 1, 2 or 3) it is

used a simple relation among dimension, number of

blocks that is necessary to recover them and the size

of the blocks. It is expressed such as:

d =

log N

log (1/L)

where N is the number of blocks with side L of que

recovering and d is the dimension. In a log-log graph,

this relation is translated as a line. The line’s slope is

the Fractal Dimension d (Feder, 2000) (07, 2004).

2.4 Methodology

For the calculus of the Fractal Dimension of each

class, it was developed an algorithm that obtains the

approximate values of the Fractal Dimension of an

image fragment. The algorithm receives for its in-

put a fragment of satellite image whose its borders

were identiﬁed. It is a binary image, just containing

the information of the limits of the interest class. The

input image is splitted in squares (or blocks) every

time minor, counted in number of pixels. For each

square size L, are counted the number of squares ”N”

that contain a piece of the image (it embroiders). The

output generated is a ﬁle containing the values of the

logarithm of L and the logarithm of N. At the end, it is

made the linear regression of the data of that ﬁle, and

the angular coefﬁcient of that straight line represents

the Fractal Dimension of the image. The experiments

were accomplished with the images classiﬁed by ML.

That classiﬁed image was submitted to the detection

of borders by the Method Canny (W. Gonzalez, 2000)

in the Software MATLAB. The image was submitted

to the detection of borders several times, modifying

the thresholds of the method Canny, in order to ob-

serve the results with more or less ”noise” of the de-

tection. The initial thresholds, given automatically by

the Software, they were 0,0063 and 0,0156. These

are, respectively Low Threshold and High Thresh-

old (parameters), in other words, the thresholds min-

imum and maximum. After the detection of borders,

they were cut out of the image areas according to the

classes of interest. Those cut out areas were used

as data of entrance of the algorithm of counting of

blocks for Dimens

ao Fractal’s determination. The re-

sults of those initial experiments are presented in the

next item.

2.5 Results of the Experiments with

Fractals

Table 1 illustrates the results obtained for the varia-

tion of the thresholds of the Fractais Dimension of the

classes Not-forest and Deforestation.

ICINCO 2005 - ROBOTICS AND AUTOMATION

472

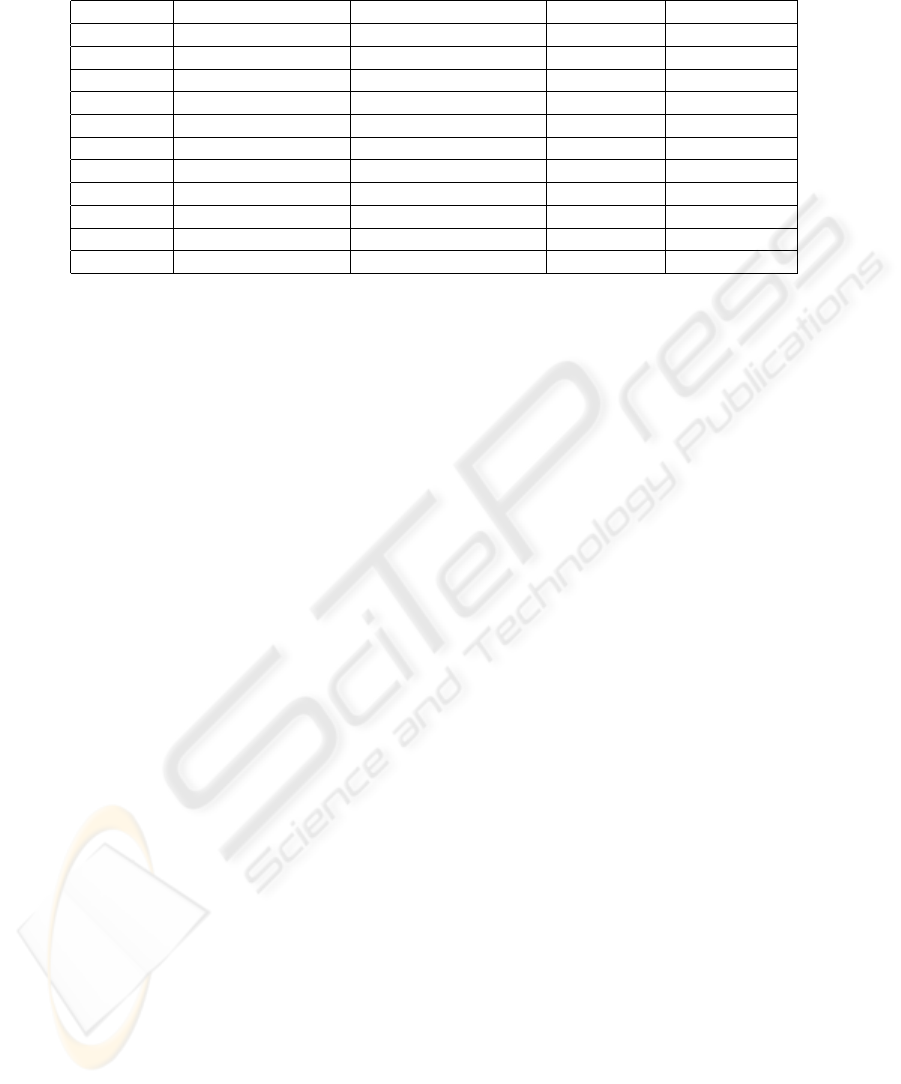
Table 1: Results of Fractal Dimension

SAMPLE LOW TRESHOLD HIGH TRESCHOLD No-Forest Deforestment

1 0.0004 0.0010 1.53709412 1.46204114

2 0.0008 0.0020 1.53537869 1.45986021

3 0.0012 0.0030 1.53410149 1.45847464

4 0.0016 0.0040 1.53297484 1.45847464

5 0.0020 0.0050 1.53107572 1.45847464

6 0.0024 0.0060 1.52993512 1.45847464

7 0.0028 0.0070 1.52984762 1.45847464

8 0.0032 0.0080 1.52922928 1.45847464

9 0.0036 0.0090 1.52905297 1.45847464

10 0.0040 0.0100 1.52799046 1.45847464

11 0.0080 0.0200 1.51408172 1.46

3 INITIAL EXPERIMENTS WITH

TAINHAS IMAGES

The image which were made the experiments de-

scribed in this section referred to the Tainhas region

in Rio Grande do Sul Province, that contains a Na-

tional Preservation Forest (FLONA), with great con-

centration of pinus and araucaria. This image was

obtained by CCD sensor of CBERS-II satellite. The

UTM coordinates of latitute is 551050.191413 and

564050.191413 and longitude is 6735848.537342 and

6752628.537342. The image was submitted to the

classiﬁers MAXVER and to RNAs, as in the previ-

ous work.They were deﬁned 8 classes, for the iden-

tiﬁcation of the main elements of the image: Field,

Bare Soil, Road, Araucaria, Pinus, Native, Cloud and

Shadow.

Using the same methodology used with the image

of Rond

onia, they were mounted bases for training

and test of both methods. Of the 432 points in that

the ﬁeld truth is had, became separated in two bases

of 216 points, each a containing 27 examples of each

class.

After the training of each classiﬁer, a confusion

head ofﬁce is set up on the test base, in order to if

it veriﬁes how many p

ıxeis they were classiﬁed cor-

rectly and which p

ıxeis were designated erroneously

to other classes. The results of those head ofﬁces will

be presented in the next section of that paper, that also

shows the result of the classiﬁcation of the whole im-

age.

3.1 Results of Classiﬁcation

Starting from the experiments accomplished with the

chosen techniques had been generated the confusion

head ofﬁces for both methods. The confusion matrix

shows how much the classiﬁer of images confuses a

class with other.

For this the exits are compared generated by the

methods for each p

ıxel and the base of examples,

that it possesses the ﬁeld truth. The diagonal of the

confusion matrix shows as the method got right, in

other words, the pixels that were classiﬁed correctly

in agreement with the ﬁeld truth.

The Tables 2 and 3 show the result of the confusion

head ofﬁces for the methods MAXVER and Neural

Networks, respectively:

4 CONCLUSIONS AND FUTURE

WORKS

In the accomplished study, being used the methods of

ML and Neural Networks, it was veriﬁed that both

methods didn’t get to distinguish some areas of the

image; to know, confusion between the classes For-

est of Araucaria and Forest of Pinus. It is observed

in the histograms of the distribution of the grayscale

of the classes, that points certain classes that locate

in the same band of values exist, what hinders to

the nets neurais on top the learning of those infor-

mation. Moreover, in this scope it is considered ad-

vantageous the use of Neural Networks in the classi-

ﬁcation of images, once it allows the incorporation of

other types of information on the image, as the use

of techniques that considers dimensions fractals and

even topographical information of the image, being

compared with ML, that consider only the grayscale

of the component bands of the image to be classiﬁed.

The use of the fractais intends to supply additional

information them to allow a better identiﬁcation of

classes in that there is confusion with the classiﬁca-

tion methods used. It is noticed, for the detection of

borders, that their surfaces tend to present different

patterns between the classes. One of the main differ-

ences between an area of deforestation and one of no

forest seen in it is the level of irregularity of their bor-

A STUDY OF CLASSIFICATION TECHNIQUES APPLIED TO CBERS SATELLITE IMAGES

473

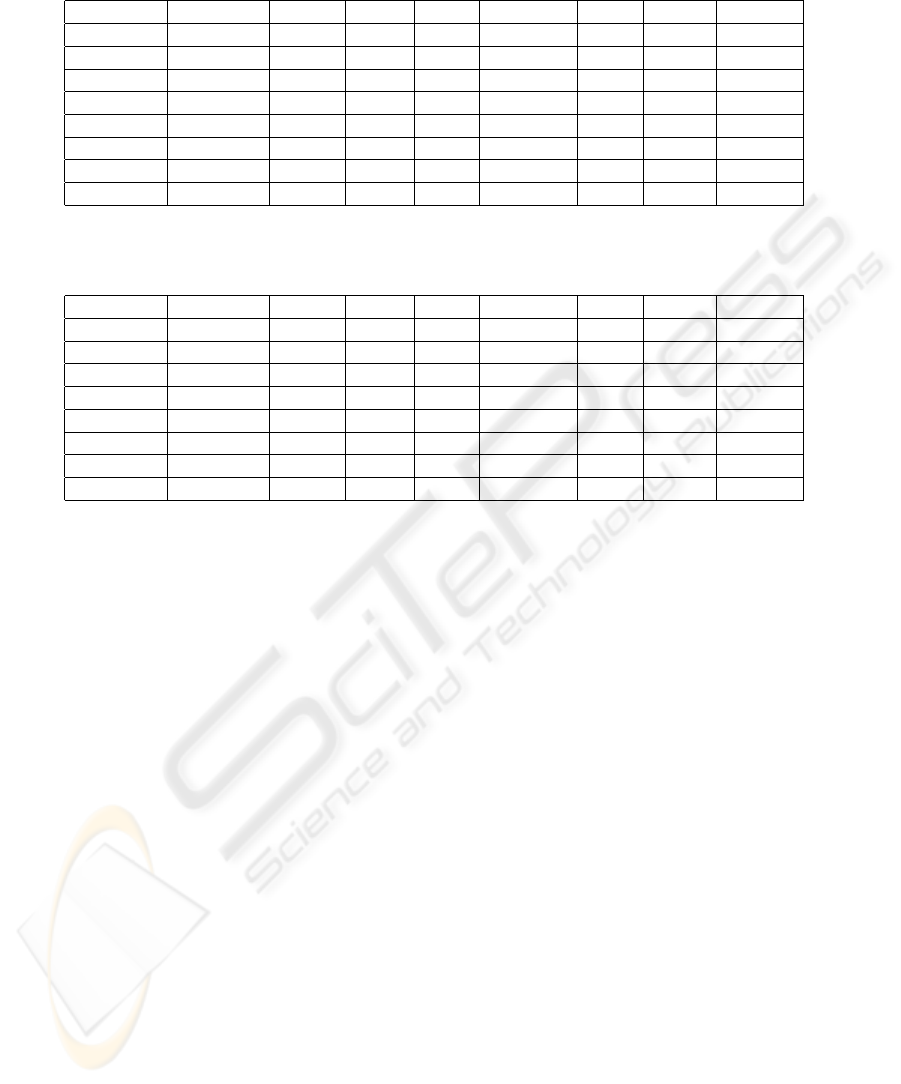
Table 2: Matrix of Confusion of Maximum Likelihood

- Araucaria Native Pinus Field Bare Soil Road Cloud Shadow

Araucaria 0 0 27 0 0 0 0 0

Native 0 27 0 0 0 0 0 0

Pinus 0 0 9 0 0 0 0 18

Field 0 0 8 0 0 19 0 0

Soil 0 8 0 0 19 0 0 0

Highway 0 0 0 1 0 26 0 0

Cloud 0 0 0 0 0 0 27 0

Shadow 0 1 0 0 0 0 0 26

Table 3: Matrix of Confusion of Neural Networks

- Araucaria Native Pinus Field Bare Soil Road Cloud Shadow

Araucaria 0 0 27 0 0 0 0 0

Native 0 27 0 0 0 0 0 0

Pinus 0 0 20 0 0 0 7 0

Field 0 0 9 9 9 0 0 0

Soil 0 0 0 0 27 0 0 0

Highway 0 0 0 9 0 18 0 0

Cloud 0 0 0 0 0 0 27 0

Shadow 0 0 0 0 1 0 0 26

ders. In fact, the areas deforested by the man tend to

be more regularly delimited than those of savannah

(no forest). In relation to the image of Tainhas, it is

known that exist areas in which araucarias present like

capons, while the pinus, that they were inserted in the

area through the human action, have a more poligo-

nal aspect. In spite of the possibility of the borders

themselves don’t constitute in fractals, in the strict

sense of the term, it is noticed that the use of estimates

of dimensions fractals can accuse such difference, re-

sulting in larger values for savannahs and smaller for

deforestations (due to the human action). That was

veriﬁed in the results obtained until the moment. The

information regarding dimension fractal of the classes

will be applied in the improvement of the accuracy

in the identiﬁcation of areas of interest together with

ML and ANNs, constituting a hybrid model of clas-

siﬁcation of satellite images. It is waited through this

work that is developed a robust classiﬁer that it sup-

plies the needs of the user’s accuracy, reducing the

parametrization difﬁculties and deﬁciencies found in

the conventional methods of classiﬁcation of images

by pixel.

REFERENCES

(2004). C

alculo da Dimens

ao Fractal.

http://cftc.cii.fc.ul.pt/ICES/manual/2/calcula-

dimensao.htmlintro.

Conci, A. (2004). Gometria Fractal.

http://www.caa.uff.br/ aconci/Fractais.html.

Feder, J. (2000). Fractals. Plenum Press, S

Ao Paulo.

Haykin, S. (1999). Redes Neurais - Princ

ıpios e Pr

atica.

Bookman, Porto Alegre, 2nd edition.

W. Gonzalez, R. W. (2000). Processamento de Imagens

Digitais. Edgard Bl

ucher, S

A£o Paulo.

ICINCO 2005 - ROBOTICS AND AUTOMATION

474